Complete Solutions to Level-1(C.W.) of chapter SYSTEM OF PARTICLES of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SYSTEM OF PARTICLES |
| NARAYANA | Level-1(C.W.) |
| Number Of Questions | 64 |
| Academic Year | 2023-24 |
A system consists of two masses connected by a massless rod lies along x-axis. The distance of centre of mass from `O` is
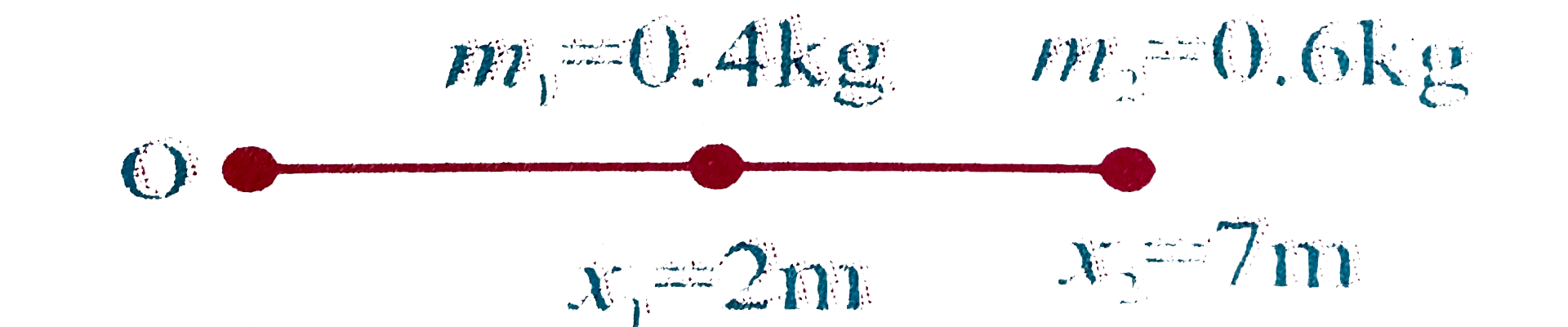
View SolutionFour particles, each of mass `1kg` are placed at the corners of a square `OABC` of side `1m`. `O` is at the origin of the coordinate system. `OA` and `OC` are aligned along positive X-axis and positive Y-axis respectively. The position vector of the centre of mass is (in `m`)
View SolutionA thick straight wire of length `pi m` is fixed at its midpoint and then bent in the form of a cricle. The shift in its centre of mass is
View SolutionA rigid body consists of a `3kg` mass located at `vec r_1=(2hat i + 5 hat j)m` and a `2kg` mass located at `vec r_2 = (4hat i +2 hat j)m`. The position of centre of mass is
View SolutionA boat of mass `40kg` is at rest. A dog of mass `4kg` moves in the boat with a velocity of `10m//s`. What is the velocity of boat (nearly)?
View SolutionTwo blocks of msses 10 kg and 30 kg are placed along a vertical line. The first block is raised through a height of 7 cm. By what distance should the second mass be moved to raise the centre of mass by 1 cm?
View SolutionTwo bodies of different masses `2kg` and `4kg` are moving with velocities `2m//s` and `10m//s` towards each other due to mutual gravitational attraction. Then the velocity of the centre of mass is
View SolutionIf two particles of masses `3kg` and `6kg` which are at rest are separated by a distance of `15 m`. The two particles are moving towards each other under a mutual force of attraction. Then the ratio of distances travelled by the particles before collision is
View SolutionTwo bodies of `6kg` and `4kg` masses have their velocity `5hati - 2 hat j + 10 hat k` and `10hat i - 2 hat j + 5 hat k` respectively. Then, the velocity of their centre of mass is
View SolutionA thin uniform rod of length `L` is bent at its mid point as shown in the figure. The distance of the centre of mass from the point `O` is

View SolutionThree identical spheres each of mass `m` and radius `R` are placed touching each other so that their centres `A,B` and `C` lie on a straight line. The position of their centre of mass from centre of `A` is
View SolutionA boy of mass `50kg` is standing at one end of a boat of length `9m` and mass `400kg`. He runs to the other end. The distance through which the centre of mass of the boat boy system moves is
View SolutionA dog weighing `5kg` is standing on a flat boat so that it is `10` metres from the shore. It walks `4m` on the boat towards the shore and then halts. The boat weighs `20kg` and one can assume that there is no friction between it and water. The dog from the shore at the end of this time is
View SolutionThe angular velocity of a rotating body is `vec omega = 4 hat i + hat j - 2 hat k`. The linear velocity of the body whose position vector `2hati + 3 hat j - 3 hat k` is
View SolutionThe area of the triangle whose adjacent sides are represented by the vector `(4hat i + 3 hat j + 4 hat k)` and `5hat i` in sq. units is
View SolutionThe angle between the vectors `(hat i + hat j + hat k)` and `( hat i - hat j -hat k)` is
View SolutionThe linear velocity of a point on the surface of earth at a latitude of `60^@` is
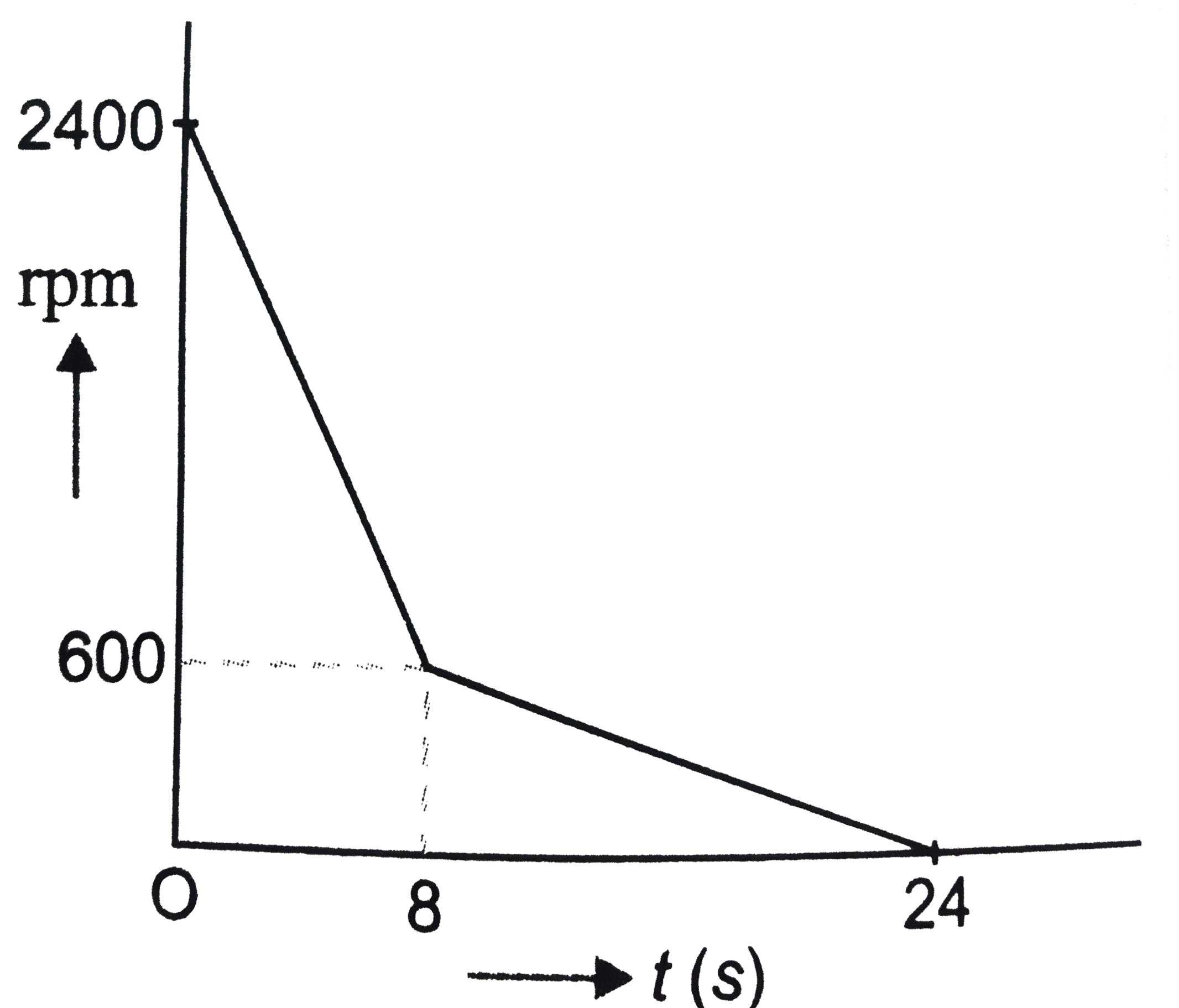
View SolutionA table fan rotating at a speed of `2400` rpm is switched off and the resulting variation of the revolution/minute time is shown in Fig. The total number of revolutions of the fan before it comes to rest is
View SolutionThe average angular velocity of the seconds hand of a watch if the seconds hand of the watch completes one revolution in `1` minute is
View SolutionThe angular displacement of a particle is given by `theta =t^3 + t^2 + t +1` then, its angular velocity at `t=2` sec is …… `rad s^(-1)`
View SolutionThe angular displacement of a particle is given by `theta =t^3 + t^2 + t +1` then,the angular acceleration of the particle at `t=2` sec is …….`rad s^(-2)
View SolutionA stationary wheel starts rotating about its own axis at uniform rate amgular acceleration `8rad//s^(2)`.The time taken by its to complete `77` rotation is
View SolutionA stationary wheel starts rotating about its own axis at constant angular acceleration. If the wheel completes `50` rotations in first `2` seconds, then the number of rotations mades by it in next two seconds is
View SolutionIf `vec F = 2 hat i - 3 hat j N` and `vec r = 3 hat i + 2 hat j m` then torque `vec tau` is
View SolutionA crowbar of length `120 cm` has its fulcrum situated at a distance of `20 cm` from the load. The mechanical advantage of the crow bar is
View SolutionThree particles of masses `1gm, 2gm & 3gm` are at `1cm, 2cm & 3cm` from the axis of rotation respectively then the moment of inertia of the system & radius of gyration of the system respectively are …. `gm cm^2` and ….. `cm`
View SolutionA hoop of mass `500gm` & radius `10cm` is placed on a nail, then the moment of inertia of the hoop, when it is rotated about the nail will be ____`kgm^2`
View SolutionThe ratio of moments of inertia of two solid spheres of same mass but densities in the ratio `1:8` is
View SolutionThe radius of a solid sphere is `R` and its density `D`. When it is made to rotate about an axis passing through any diameter of sphere, expression for its moment of inertia is
View SolutionFour point size bodies each of mass `M` are fixed at four corners of a light square frame of side length `L`. The moment of inertia of the four bodies about an axis perpendicular to the plane of frame and passing through its centre is
View SolutionFour particles each of mass `m` are placed at the corners of a square of side length `l`. The radius of gyration of the system about an axis perpendicular to the plane of square and passing through its centre is
View SolutionFour particles each of mass `m` are placed at the corners of a square of side length `l`. The radius of gyration of the system the moment of inertia of four bodies about an axis perpendicular to the plane of frame and passing through a corner is
View SolutionFour particles each of mass `m` are placed at the corners of a square of side length `l`. The radius of gyration of the system the moment of inertia of four bodies about an axis passing through opposite corners of frame is
View SolutionFour particles each of mass `m` are placed at the corners of a square of side length `l`. The radius of gyration of the system the moment of inertia of four bodies about an axis passing through any side of frame is
View SolutionThe diameter of a fly wheel is `R`. Its coefficient of linear expansion is `alpha`. If its temperature is increased by `deltaT` the percentage increase in its moment of inertia is
View SolutionThree point sized bodies each of mass `M` are fixed at three corners of light triangular frame of side length `L`. About an axis perpendicular to the plane of frame and passing through centre of frame the moment of inertia of three bodies is
View SolutionThree point sized bodies each of mass `M` are fixed at three corners of light triangular frame of side length `L`. About an axis perpendicular to the plane of frame and passing through a corner of frame the moment of inertia of three bodies is
View SolutionThree point sized bodies each of mass `M` are fixed at three corners of light triangular frame of side length `L`. About an axis passing through any side of frame the moment of inertia of three bodies is
View SolutionThe radius of gyration of body is `18cm` when it is rotating about an axis passing through centre of mass of body. If radius of gyration of same body is `30cm` about a parallel axis to first axis then, perpendicular distance between two parallel axes is
View SolutionThe position of axis of rotation of a body is changed so that its moment of inertia decreases so that its moment of inertia decreases by `36%.` The `%` change in its radius of gyration is
View SolutionA diatomic molecule is formed by two atoms which may be treated as mass points `m_1` and `m_2` joined by a massless rod of length `r`. Then the moment of inertia of molecule about an axis passing through centre of mass and perpendicular to the rod is:
View Solution`I` is moment of inertia of a thin square plate about an axis passing through opposite corners of plate. The moment of inertia of same plate about an axis perpendicular to the plane of plate and passing through its centre is
View SolutionMass of thin long metal rod is `2kg` and its moment of inertia about an axis perpendicular to the length of rod and passing through its one end is `0.5 kg m^2`. Its radius of gyration is
View SolutionThe diameter of a disc is `1m`. It has a mass of `20kg`. It is rotating about its axis with a speed of `120` rotations in one minute. Its angular momentum in `kg m^2//s` is
View SolutionIf the earth were to suddenly contract to `1//n^(th)` of its present radius without any change in its mass, the duration of the new day will be nearly
View SolutionA particle performing uniform circular motion gas angular momentum `L`. If its angular frequency is double and its kinetic energy halved, then the new angular momentum is :
View SolutionA ballet dancer is rotating about his own vertical axis at an angular velocity `100 rpm` on smooth horizontal floor. The ballet dancer folds himself close to his axis of rotation by which is moment of inertia decreases to half of initial moment of inertia then his final angular velocity is
View SolutionA thin circular ring of mass M and radius r is rotating about its axis with a constant angular velocity `omega`, Two objects, each of mass m, are attached gently to the opposite ends of a diameter of the ring. The wheel now rotates with an angular velocity `omega=`
View SolutionA ballet dancer is rotating at angular velocity `omega` on smooth horizontal floor. The ballet dancer folds his body close to his axis of rotation by which his radius of gyration decreases by `1//4^(th)` of his initial radius of gyration, his final angular velocity is
View SolutionA particle of mass `m` is moving along a circle of radius `r` with a time period `T`. Its angular momentum is
View SolutionIf the radius of earth shrinks by `0.2%` without change in its mass, the `%` change in its angular velocity is
View SolutionA metallic circular plate is rotating about its axis without friction. If the radius of plate expands by `0.1%` then the `%` change in its moment of inertia is
View SolutionA constant torque acting on a uniform circular wheel changes its angular momentum from `A` to `4A` in `4sec`. The torque acted on it is
View SolutionDensity remaining constant, if earth contracts to half of its present radius, duration of the day would be (in minutes)
View SolutionA mass is whirled in a circular path with an angular momentum `L`. If the length of string and angular velocity, both are doubled, the new angular momentum is
View SolutionAn automobile engine develops `100` kilo`-`watt, when rotating at a speed of `1800 rev//min`. Find the torque developed by it.
View SolutionAn electric motor exerts a constant torque `5Nm` on a fly wheel by which it is rotated at the rate of `420 rpm` The power of motor is
View SolutionA shaft rotating at 3000 rpm is transmitting a power of `3.14 KW`. The magnitude of the driving torque is
View SolutionA solid sphere rolls down without slipping from rest on a `30^@` incline. Its linear acceleration is
View SolutionA hollow sphere rolls down a `30^@` incline of length `6m` without slipping. The speed of centre of mass at the bottom of plane is
View SolutionFor a body rolling along a level surface, the translational and rotational `K.E.` are equal. The body is
View SolutionA ring and a disc of same mass roll without slipping along a horizontal surface with same velocity. If the `K.E.` of ring is `8J`, then that of disc is
View SolutionWhen a hollow sphere is rolling without slipping on a rough horizontal surface then the percentage of its total `K.E.` which is translational is
View SolutionIf a sphere of mass `2kg` and diameter `10cm` is rolling at speed of `5ms^(-1).` Its rotational kinetic energy is
View Solution
Level-1(C.W.) questions and complete solutions for chapter SYSTEM OF PARTICLES of NARAYANA PHYSICS (HINGLISH) of Class 11