Complete Solutions to Level-VI of chapter SYSTEM OF PARTICLES of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SYSTEM OF PARTICLES |
| NARAYANA | Level-VI |
| Number Of Questions | 78 |
| Academic Year | 2023-24 |
The point `P` of a string is pulled up with an acceleration `g`. Then the acceleration of the hanging disc (w.r.t ground) over which the string is wrapped, is
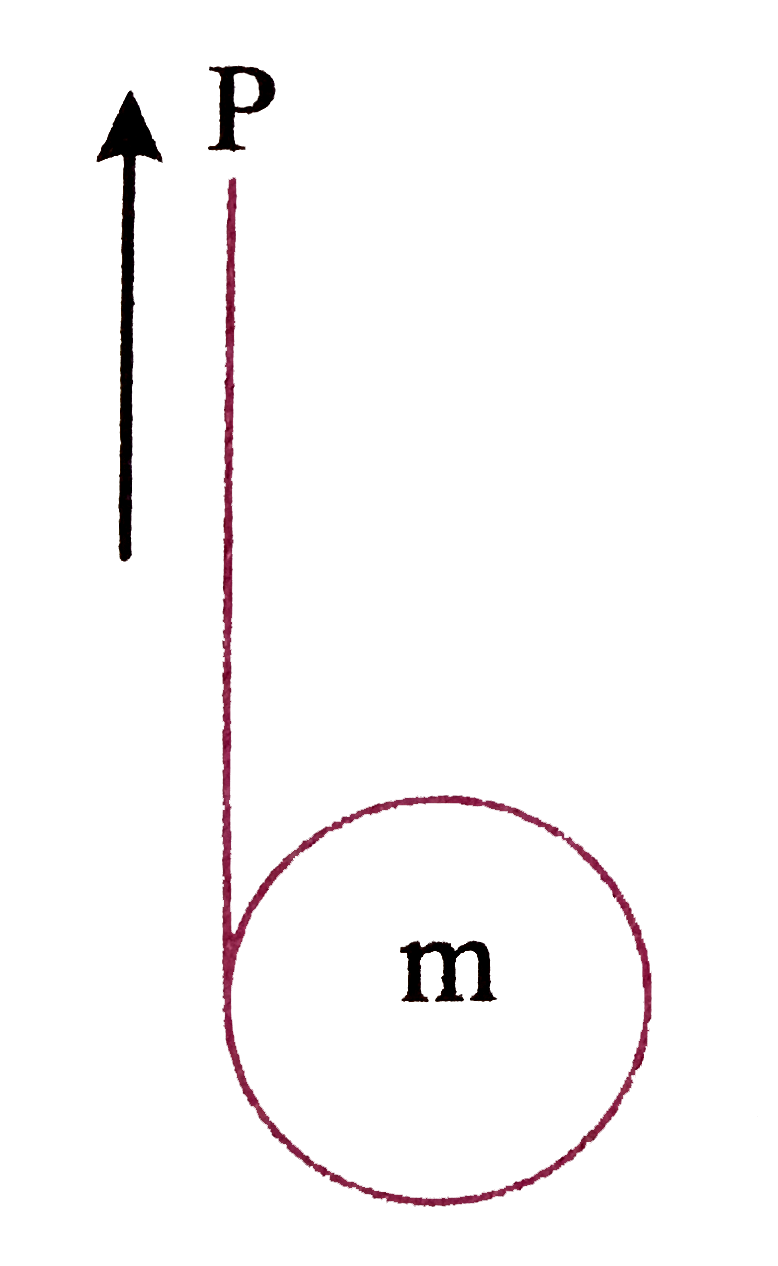
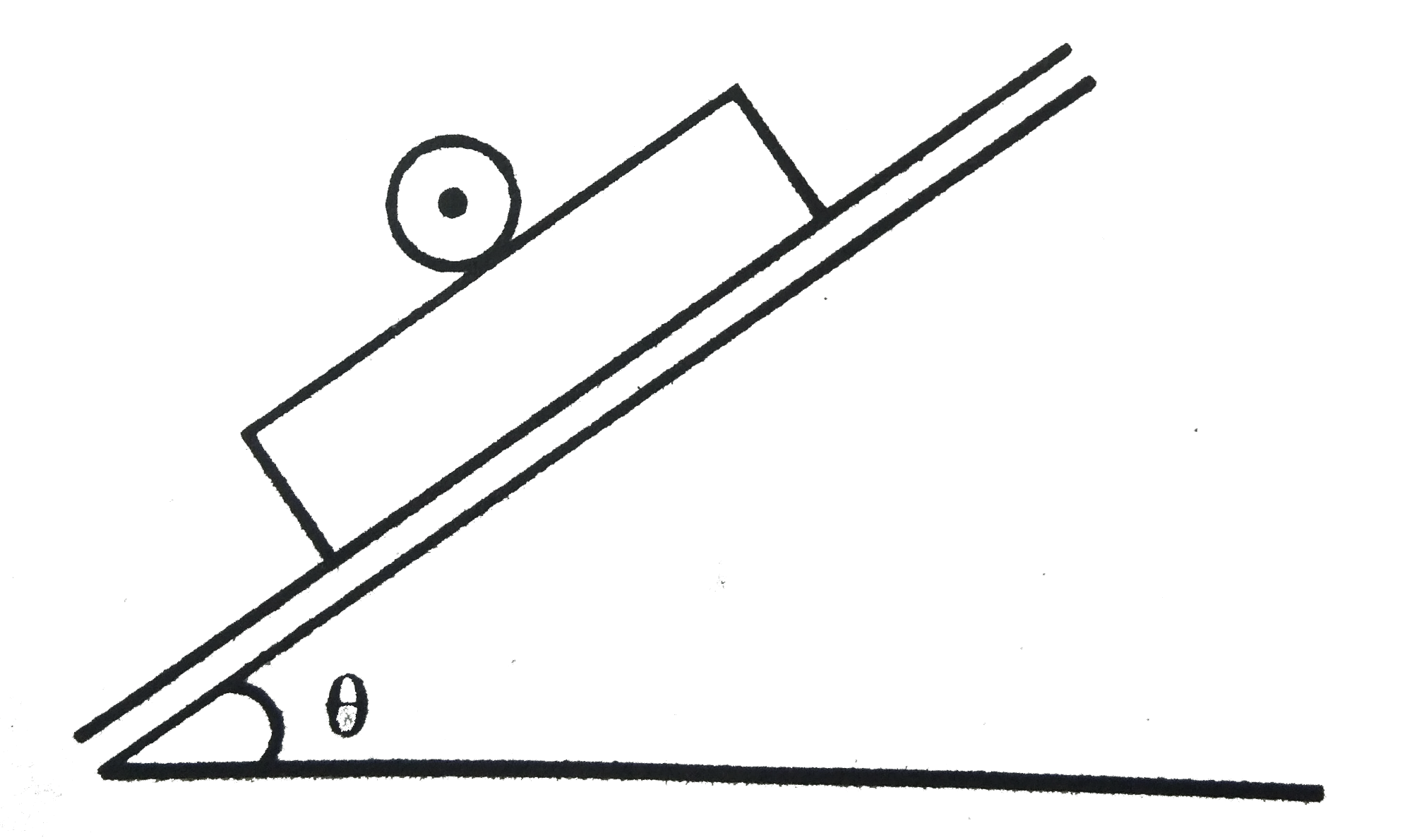
View SolutionA plank of mass `M` is placed over smooth inclined plane and sphere is also placed over the plank. Friction is sufficient between sphere and plank. If plank and sphere are released from rest, the frictional force on sphere is -
 .
.
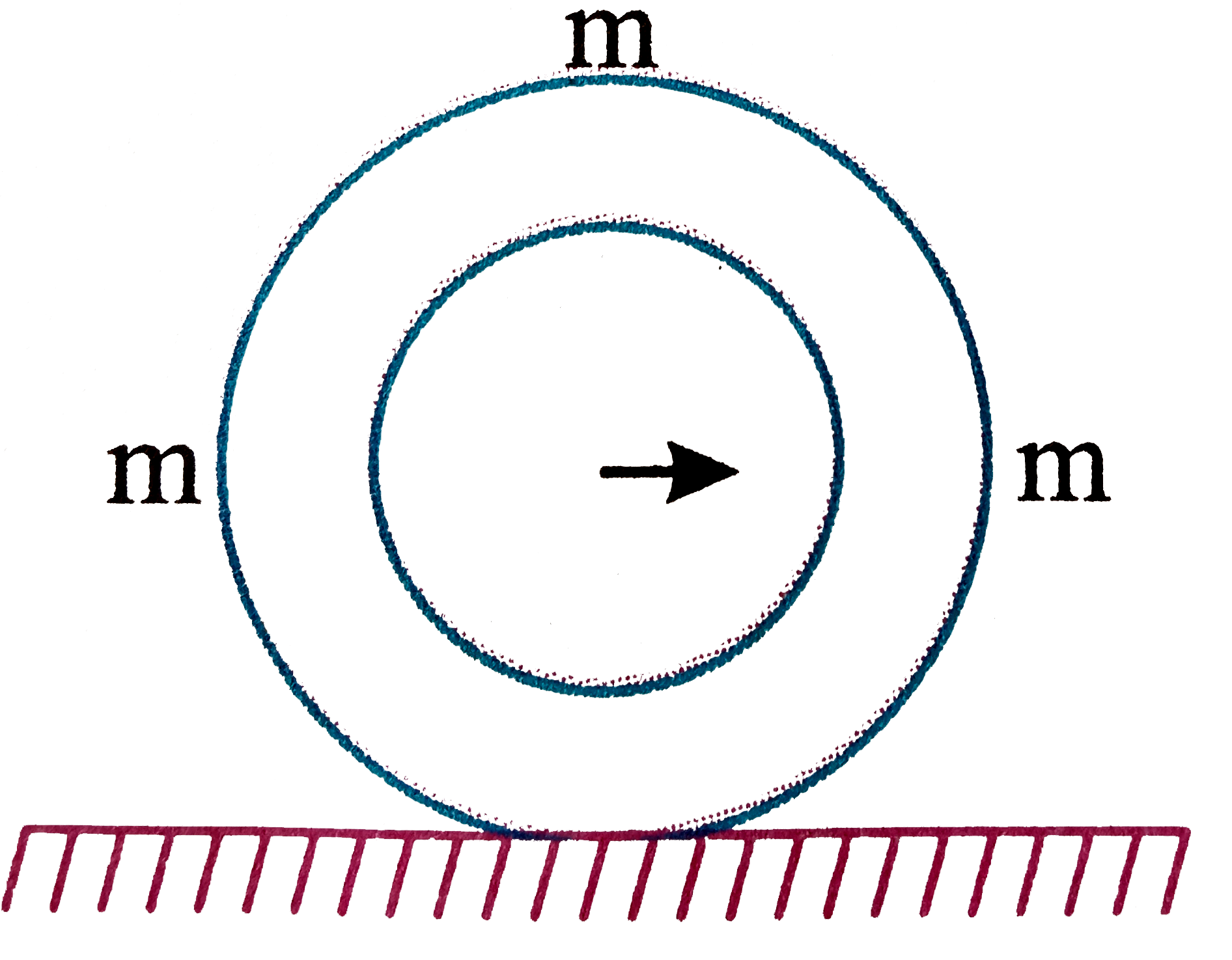
View SolutionFour beads each of mass `m` are glued at the top, bottom and the ends of the horizontal diameter of a ring of mass`m`. If the ring rolls without sliding with the velocity `v` of its, the kinetic energy of the system (beads+ring) is
View SolutionA rolling body is connected with a trolley car by a spring of stiffness `k`. It does not slide and remains in equilibrium relative to the acceleration trolley car. If the trolly car is stopped after a time `t=t_(0)`. (the rolling body touches the trolly)
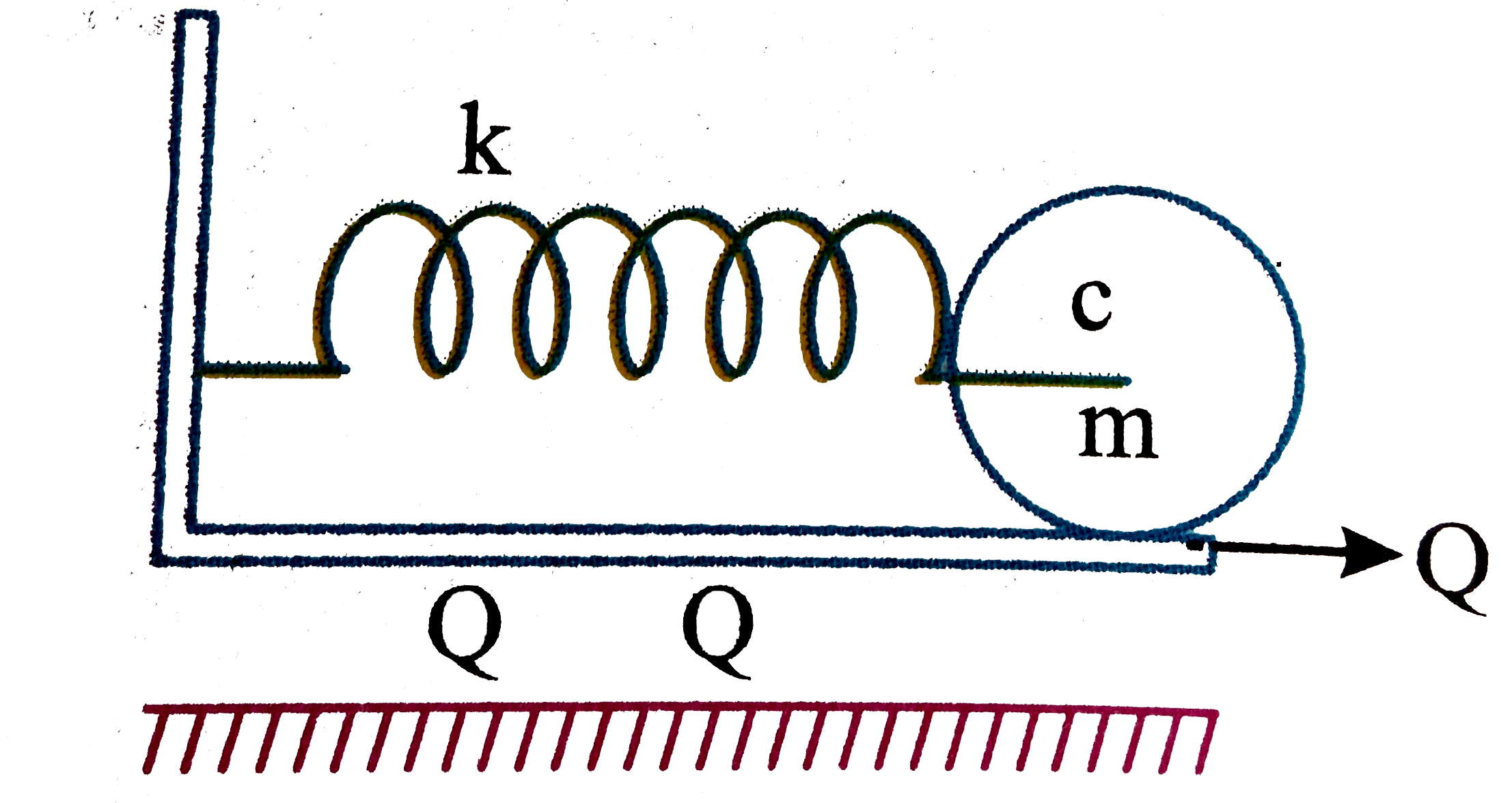
View SolutionA linear impulse `int Fdt` acts at a point `C` of the smooth rod `AB`. The value of `x` is so that the end `A` remains stationary just after the impact is

View SolutionTwo light vertical springs with equal natural length and spring constants `k_(1)` and `k_(2)` are separated by a distance`l`. Their upper end the ends `A` and `B` of a light horizontal rod `AB`. A vertical downwards force `F` is applied at point `C` on the rod. `AB` will remain horizontal in equilibrium if the distance `AC` is
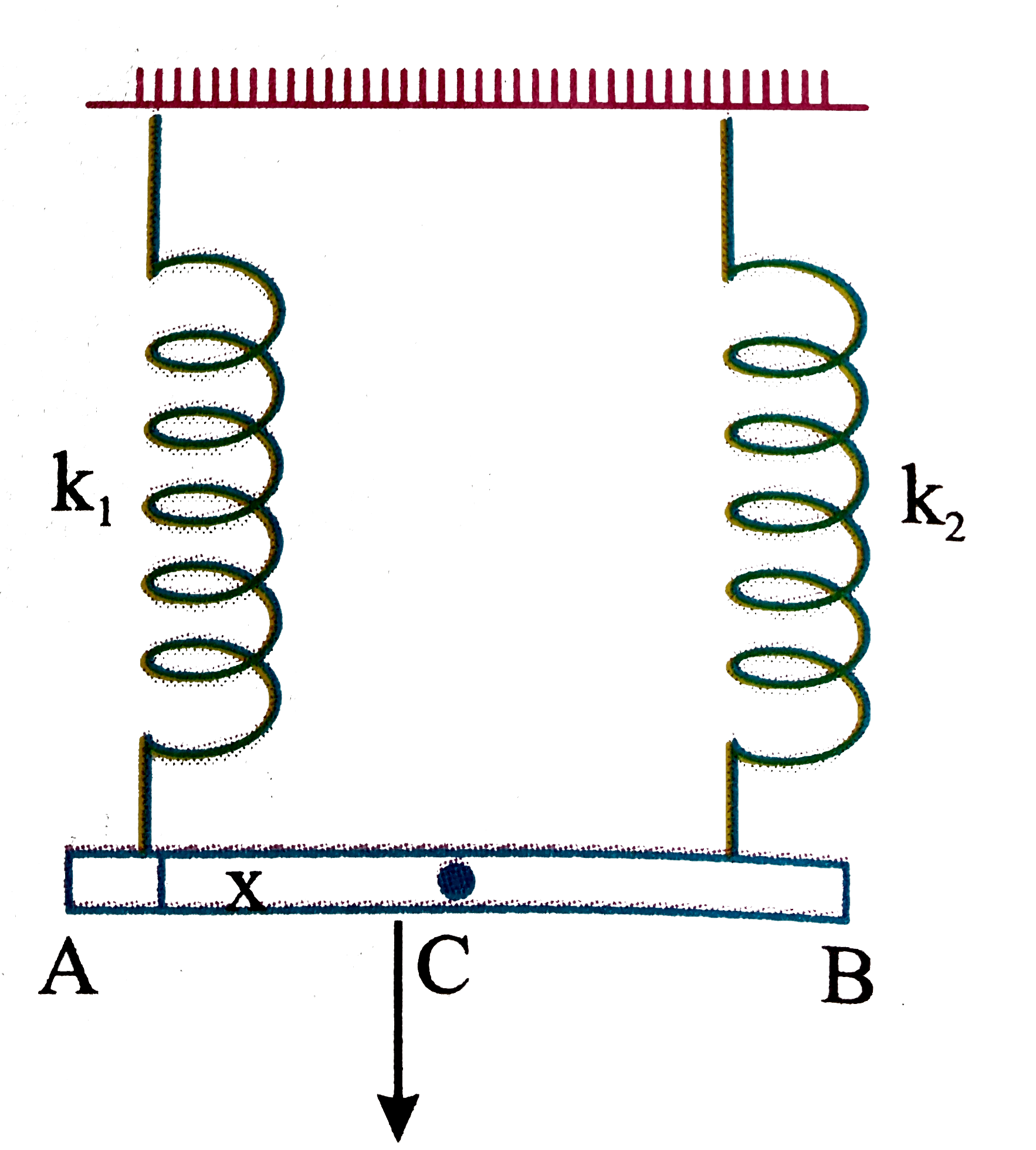
View SolutionLer l be the moment of inertia of a uniform square plate about an axis AB that passes through its centre and is parallel to two of its sides. CD is a line in the plane of the plate that passes through the centre of the plate and makes an angle `theta` with AB. The moment of inertia of the plate about the axis CD is then equal to
View SolutionTwo point masses `A` of mass `M` and `B` of mass of `4M` are fixed at the ends of a rod of length `l` and of negligible mass. The rod is set rotation about an axis perpendicular to its length with a uniform angular speed. The work required for rotating the rod will be minimum when the distance of axis of rotation from the mass `A` is at
View SolutionA conical pendulum consists of a mass `M` suspended from a string of length `l`. The mass executes a circle of radius `R` in a horizontal plane with speed `v`. At time `t`, the mass is at position `Rhat i` and has velocity `v hat j`. At time `t`, the angular momentum vector of the mass `M` about the point from which the string suspended is

View SolutionA ring of mass `m` and radius `R` is rolling down on a rough inclined plane of angle `theta` with horizontal. Plot the angular momentum of the ring about the point of contact of ring and the plane as a function of time
View SolutionA ring of mass `M` and radius `R` lies in `x-y` plane with its centre at origin as shown. The mass distribution of ring is non uniform such that, at any point `P` on the ring, the mass per unit length is given by `lamda = lamda_0 cos^2 theta` (where `lamda_0` is a positive constant). Then the moment of inertia of the ring about z-axis is :
 .
.
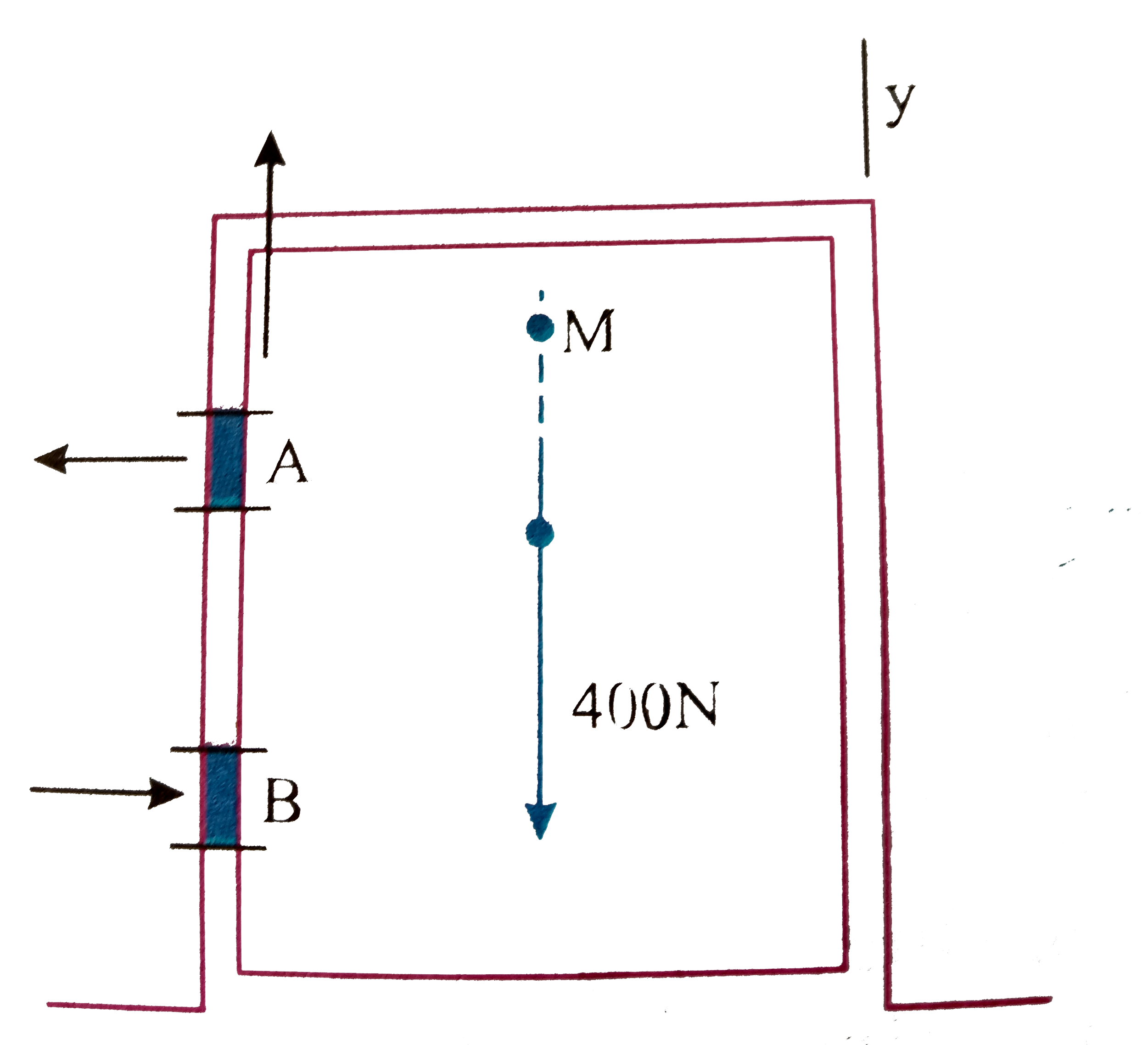
View SolutionAs shown in figure, the hinges `A` and `B` hold a uniform `400N` door in place. The upper hinge supports the entire weight of the door. Find the resultant force exerted on the door at the hinges, the width of the door is `h/2`, where `h` is the distance between the hinges.
View SolutionFind minimum height of the obstacle so that the shpere can stay in equilibrium

View SolutionIn the figure shown, suppose the compound pulley and the disc have the same angular acceleration, in clockwise direction. If `a_1` is the upward acceleration of the compound pulley's centre (inner radius `r`, outer radius `3r`), `a_2` is the downward acceleration of the while `a_3` is the upward acceleration of the centre of the disc (radius `2r`). From kinematic constraints of the thread, the relation between them is:
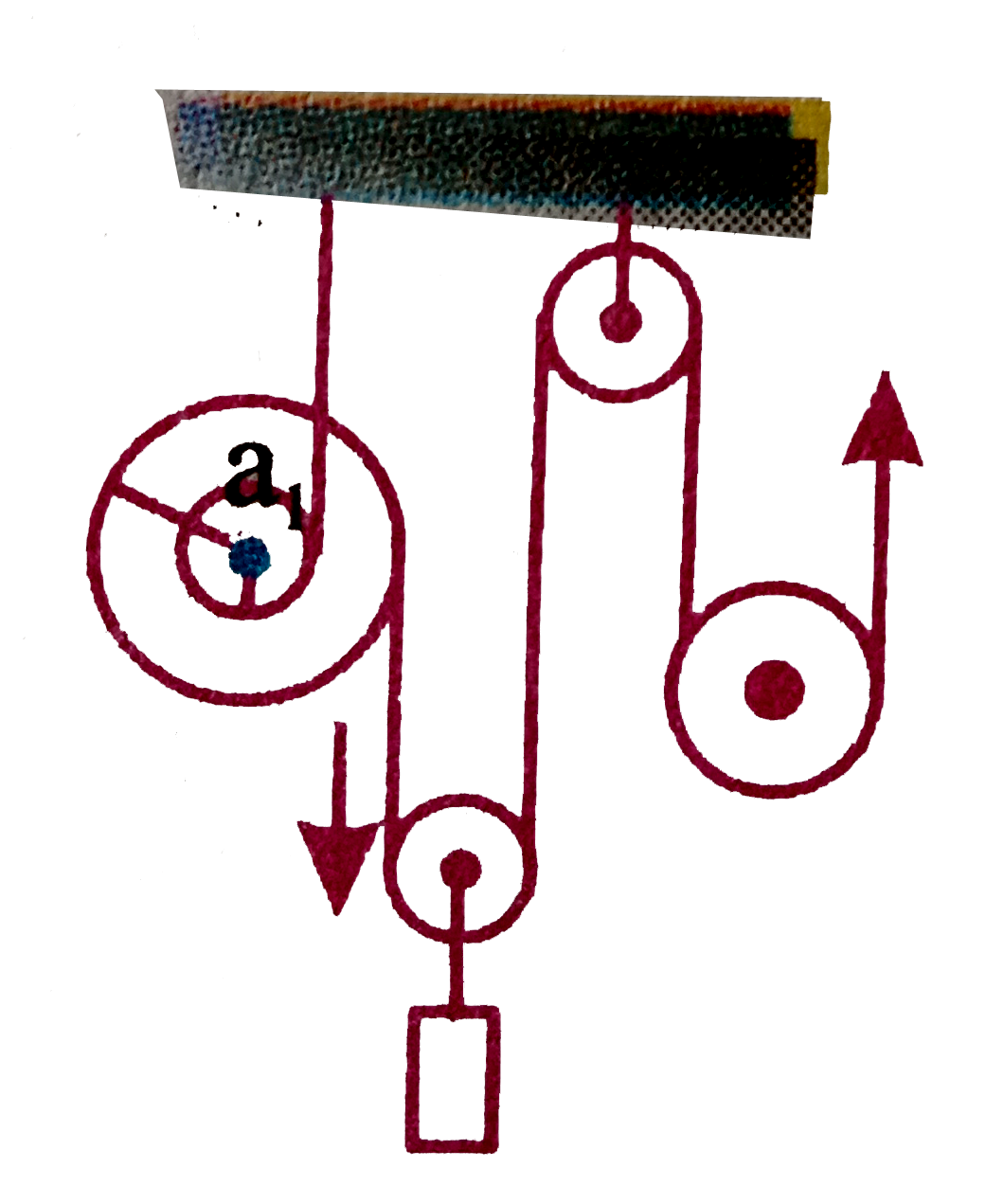
View SolutionTwo identical rings A and B are acted upon by torques `tau_(A)` and `tau_(B)` respectively. A is rotating about an axis passing through the centre of mass and perpendicular ot the plane of the ring. B is rotating about a chord at a distance `1/(sqrt(2))` times the radius of the ring. If the angular acceleration of the ring is the same, then
View SolutionA uniform solid sphere of radius `r` is rolling on a smooth horizontal surface with velocity `v` and angular velocity `omega = (v=omega r)`. The sphere collides with a sharp edge on the wall as shown in figure. The coefficient of friction between the sphere and the edge `mu=1//5`. Just after the collision the angular velocity of the sphere becomes equal to zero. The linear velocity of the surface just after the collision is equal to

View SolutionAngular acceleration of the cylinder `C` shows in the figure is (all strings and the pulley are ideal)

View SolutionA particle of mass `m` is released from rest at point `A` in the figure falling freely under gravity parallel to the vertical `Y`-axis. The magnitude of angular momentum of particle about point `O` when it reaches `B` is (where `OA=b` and `AB=h`)

View Solution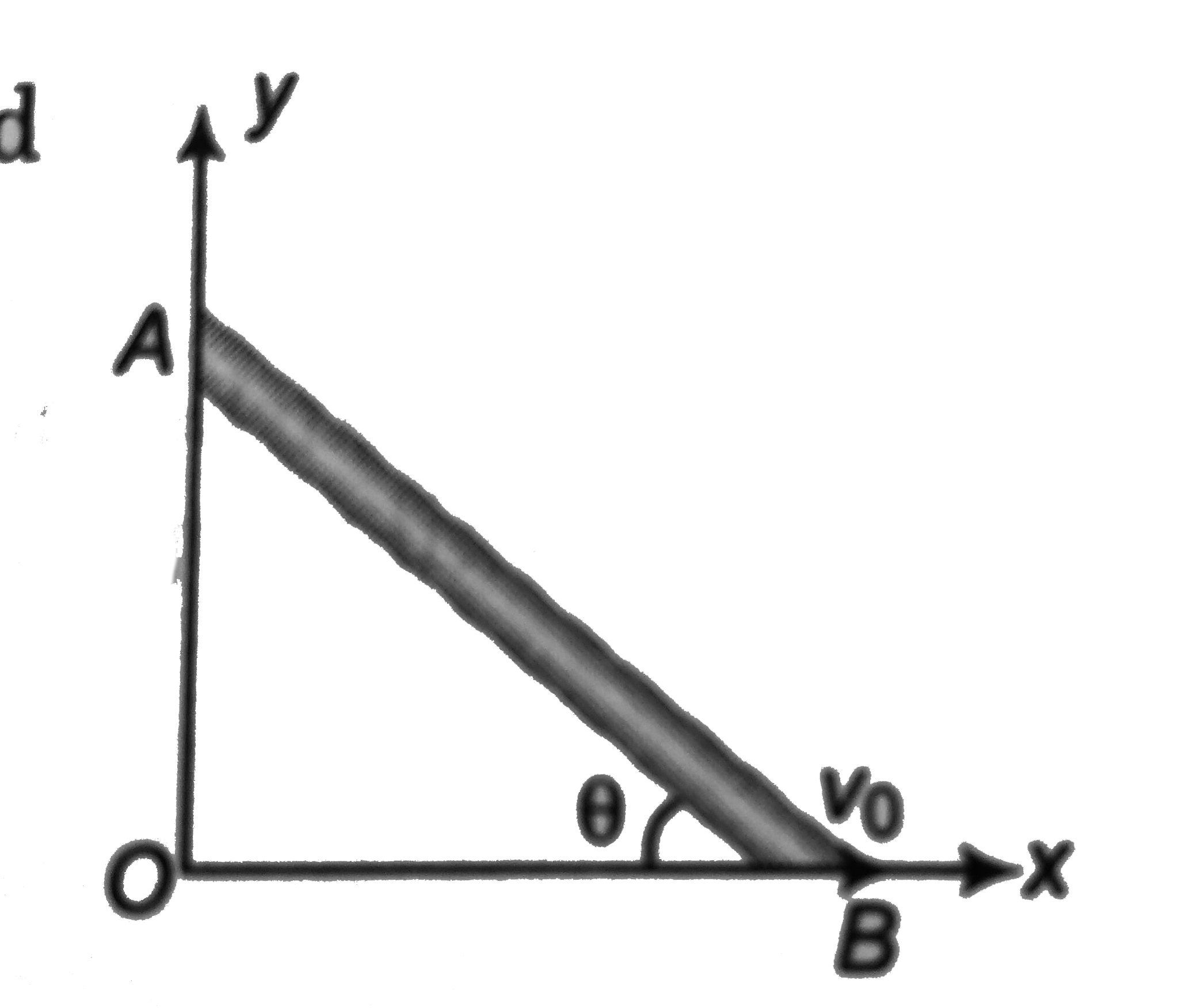
The end B of the rod AB which makes angle `theta` with the floor is being pulled with a constant velocity `v_(v)` as shown. The length of the rod is `l`.
View SolutionA block having equilateral triangular cross-section of side a and mass `m` is placed on a rough inclined surface, so that it remains in equilibrium as shown in figure. The torque of normal force acting on the block about its centre of mass is

View SolutionA thin horizontal uniform rod `AB` of mass `m` and length `l` can rotate freely about a vertical axis passing through its end `A`. At a certain moment, the end `B` starts experiencing a constant force `F` which is always perpendicular to the original position of the stationary rod and directed in a horizontal plane. The angular velocity of the rod as a function of its rotation angle `theta` measured relative to the initial position should be.
View SolutionA block mass `m` moves on a horizontal circle against the wall of a cylinderical room of radius `R`. The floor of the room, on which the block moves, is smooth but the friction coefficient between the wall and the block is `mu`. The block is given an initial speed `V_(0)`. the power developed by the resultant force acting on the block as a function of distance travelled `s` is
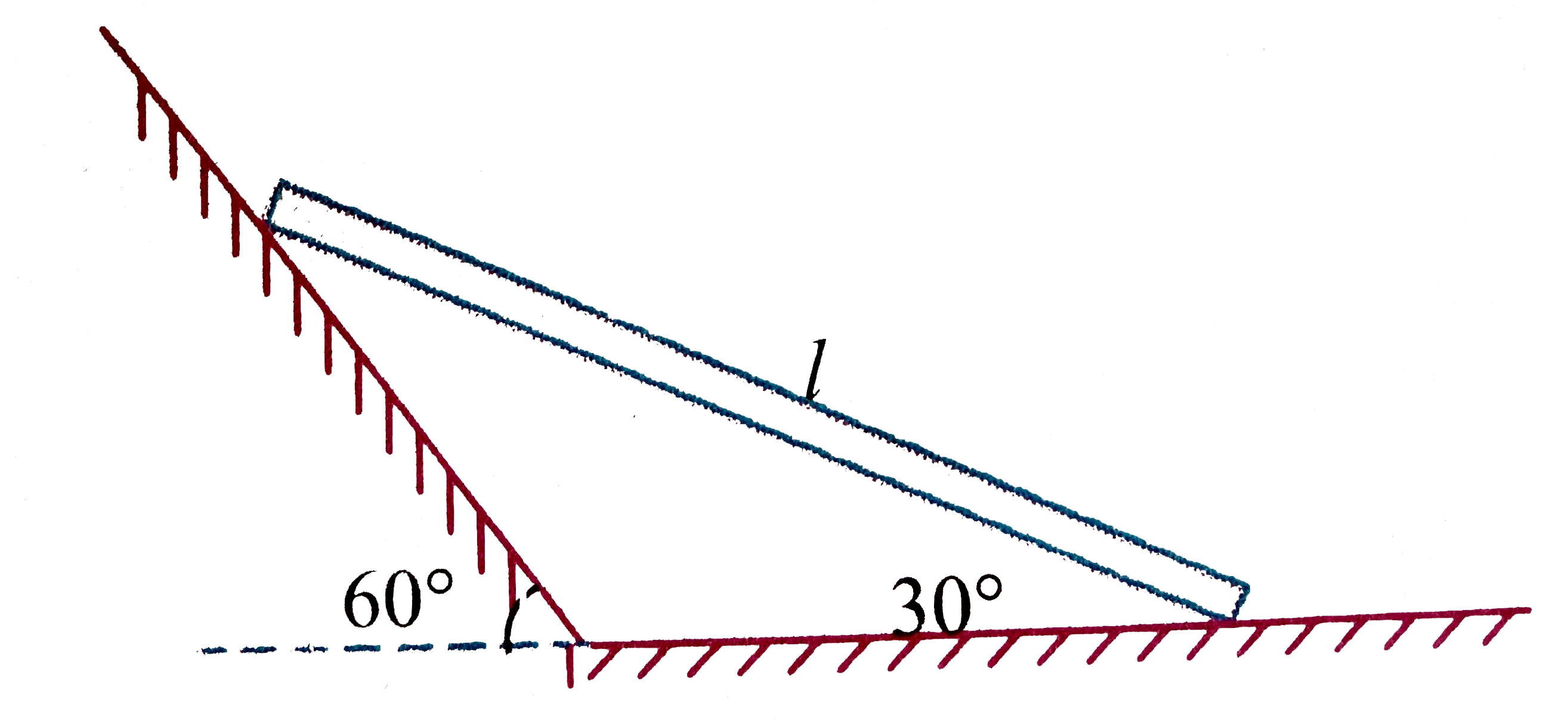
View SolutionA uniform rod of length `l` is released from the position shown in the figure. The acceleration due to gravity is `g`. There is no friction at any surface. Find the initial angular acceleration of the rod.
View SolutionConsider an arrangement shown in the figure. The pulley `P` is frictionless and the threads are massless. The mass of the spools is `m` and moment of inertia of the spool is `1/2 mR^(2)`. The mass of the disc of radius `R` is also `m`. The surface below the spool is rough to ensure pure rolling of spool. the mass of the block is `m` and the surface below the block is smooth. find the initial acceleration of the block when the system is released from rest.

View SolutionFind the moment of inertia of a hemisphere of mass `M` and radius `R` shown in the figure, about an axis `A A'` tangential to the hemisphere.

View SolutionA wheel rolls purely between a rough horizontal surface below it and a horizontal plank above it under the action of a horizontal force `F` applied on the plank. If at any time `vec(v)_(p)` and `vec(v)_(c)` represent velocity of plank and velocity and `vec(a)_(p)` and `vec(a)_(c)` represent acceleration of plank and acceleration of centre of mass of wheel respectively then which of the following is `//` are correct.

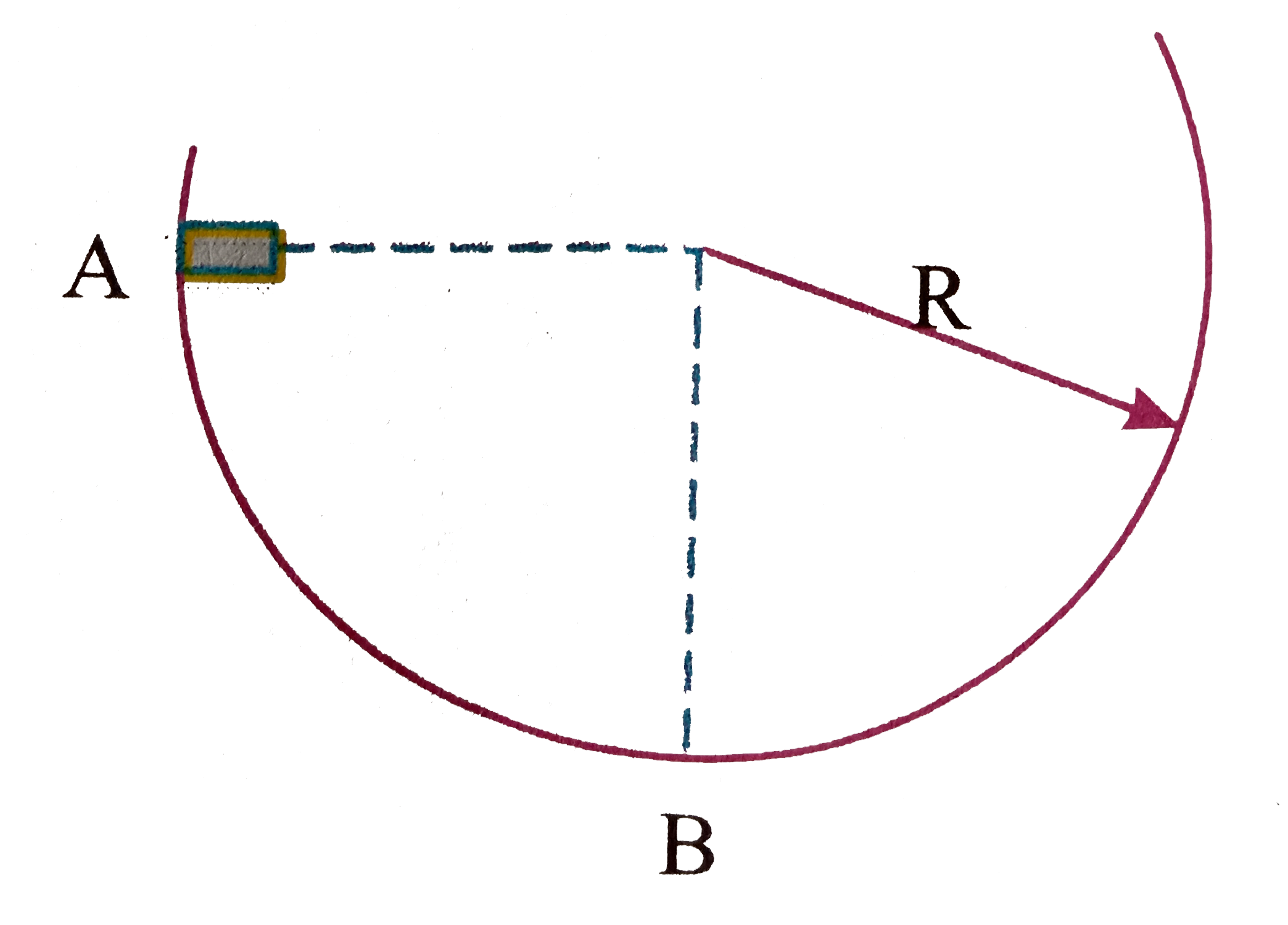
View SolutionA small block of mass `m` is released from rest from position `A` inside a smooth hemispherical bowl of radius `R` as shown in figure. Choose the wrong option (s)
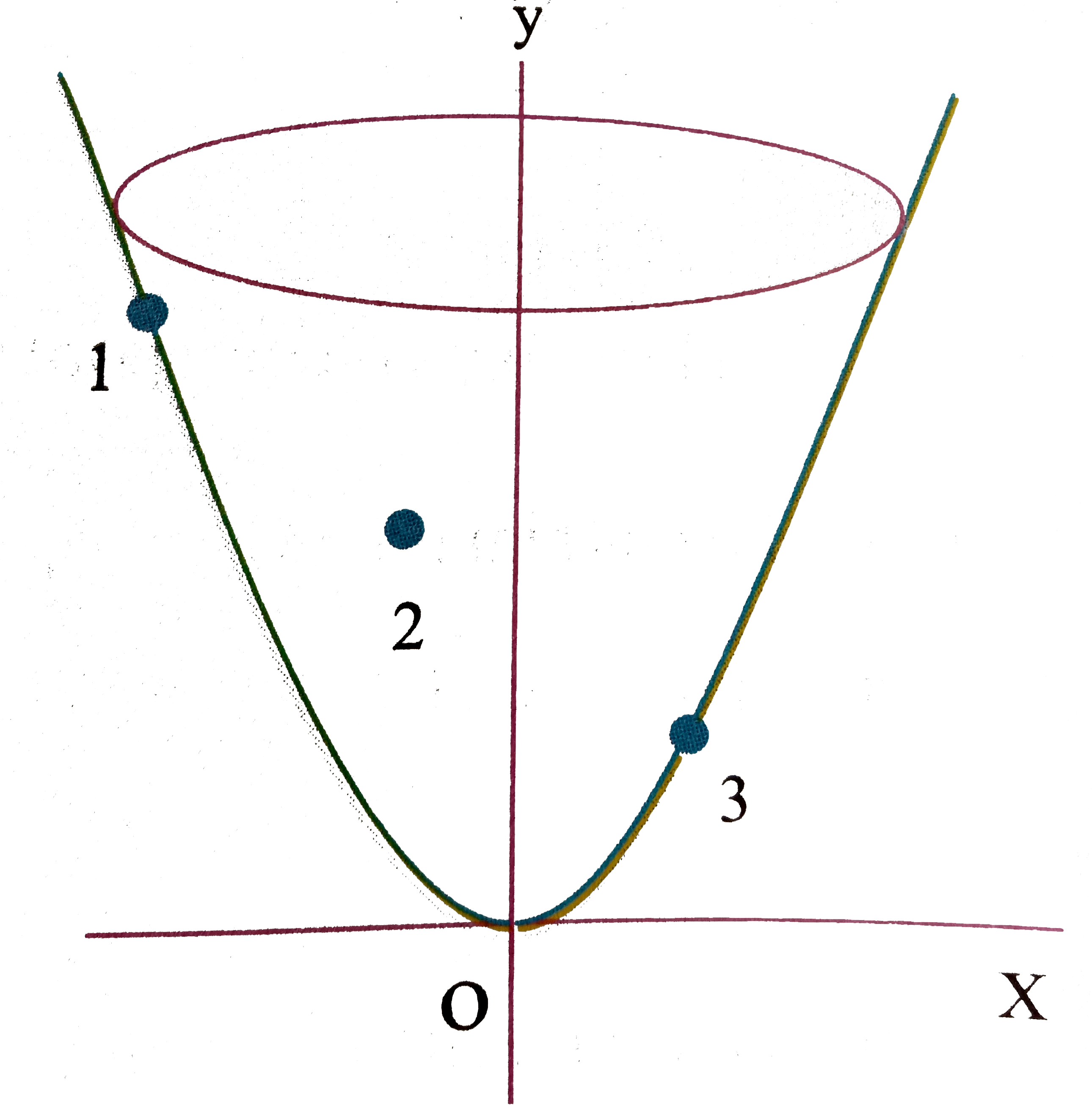
View SolutionThree particles, each of mass `m` are placed an the points `(x_(1),y_(1),z_(1)),(x_(2),y_(2),z_(2))` and `(x_(3),y_(3),z_(3))` on the inner surface of a paraboloid of revolution obtained by rotating the parabola `x^(2)=4ay` about the `y`-axis. Neglected the mass of the paraboloid. (`y`-axis. is along the vertical (a) the moment of inertia of the system about the axis of the paraboloid is `I=4ma(y_(1)+y_(2)+y_(3))`
View SolutionA massless spool of inner radius `r` outer radius `R` is placed against a vertical wall and a titled split floor as shown. A light inextensible thread is tightly wound around the spool through which a mass `m` is hainging. There exists no friction at point `A`, while the coefficient of friction between the spool and point `B` is `mu`. The angle between the two surface is `theta`

View SolutionTwo particles of masses `m_(1)` and `m_(2)` are connected with a rigid rod of length `l`. If a force `F` acts perpendicular to the rod then (`a_(1) & a_(2)` are instantaneous of `m_(1) & m_(2)`)

View SolutionA uniform solid of mass `m` is placed on a sheet of paper on a horizontal surface. The coefficient of friction between paper and sphere is `mu`. If the paper is pulled horizontally with an acceleration
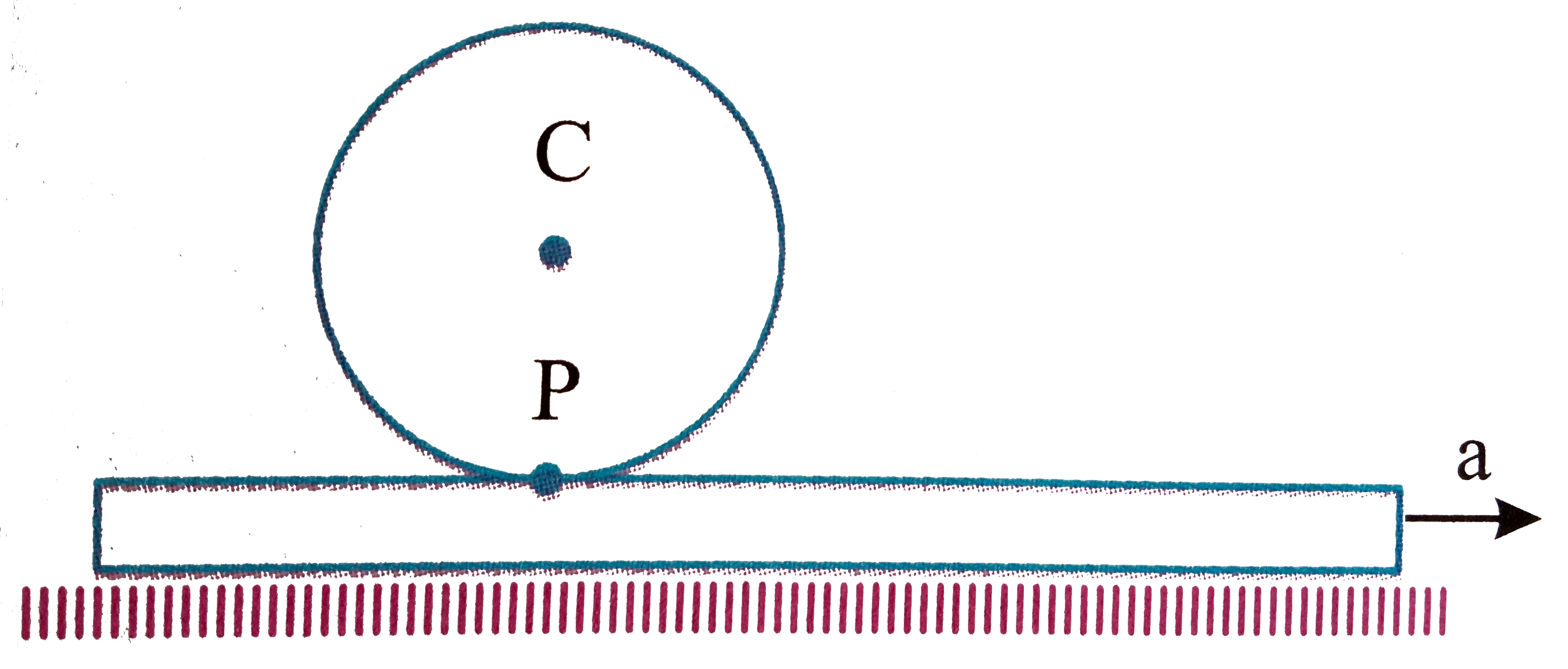
View SolutionA rigid body is in pure rotation, that is, undergoing fixed axis rotation. Then which of the following statement(s) are true?
View SolutionA rough disc of mass `m` rotates freely with an angular velocity `omega`. If another rough disc of mass `m/2` and same radius but spinning in opposite sense with angular speed `omega` is kept on the first disc. Then:
View SolutionIn the figure, the disc `D` does not slip on the surface `S`, the pulley `P` has mass and the string does not slip on it. The string is wound around the disc.

View SolutionA triangular block `ABC` of mass `m` and side `2a` lies on a smooth horizontal plane is shown. There point masses of the `m` each strikes the block at `A, B` and `C` with speed as shown. After the collision the particle come to rest. Then
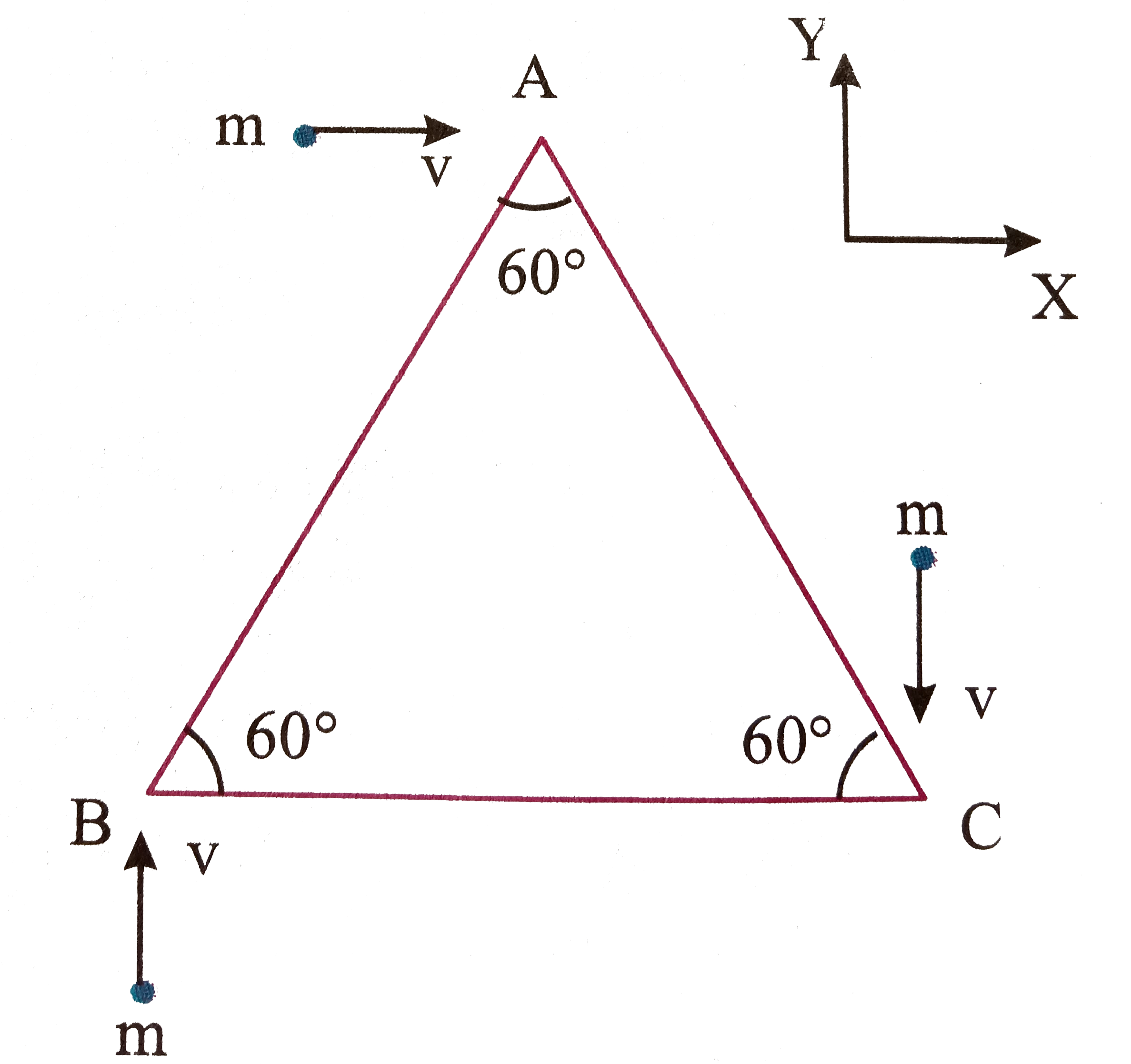
View SolutionA rod leans against a stationary cylindrical body as shown in figure, and its right end sides to the right on the floor with a constant speed `v`. Choose the correct option (s)

View SolutionThe uniform `120 N` board shown in figure is supported by two ropes. A `400 N` weight is suspended one-fourth of the way from the left end. Choose the correct options
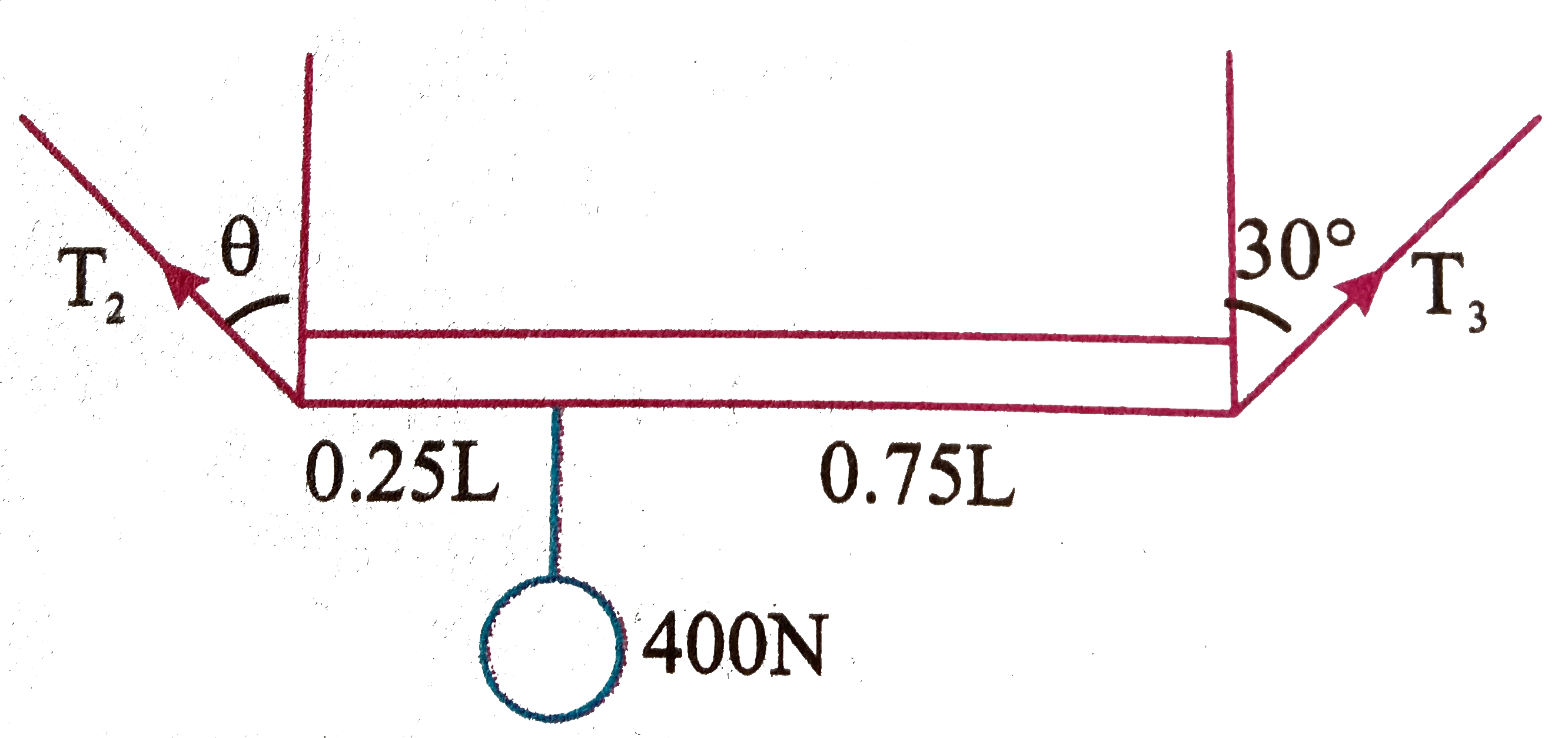
View SolutionThe `KE` and moment of inertia about the given end point of a rod of mass `m` and length `l` and cross sectional area `A` which is rotating with `omega=sqrt(g/l)` as shown in figure. Will be [density of the rod varies as `rho=rho_(0)(1+x/l),x` is the distance measured from `O`)n ]
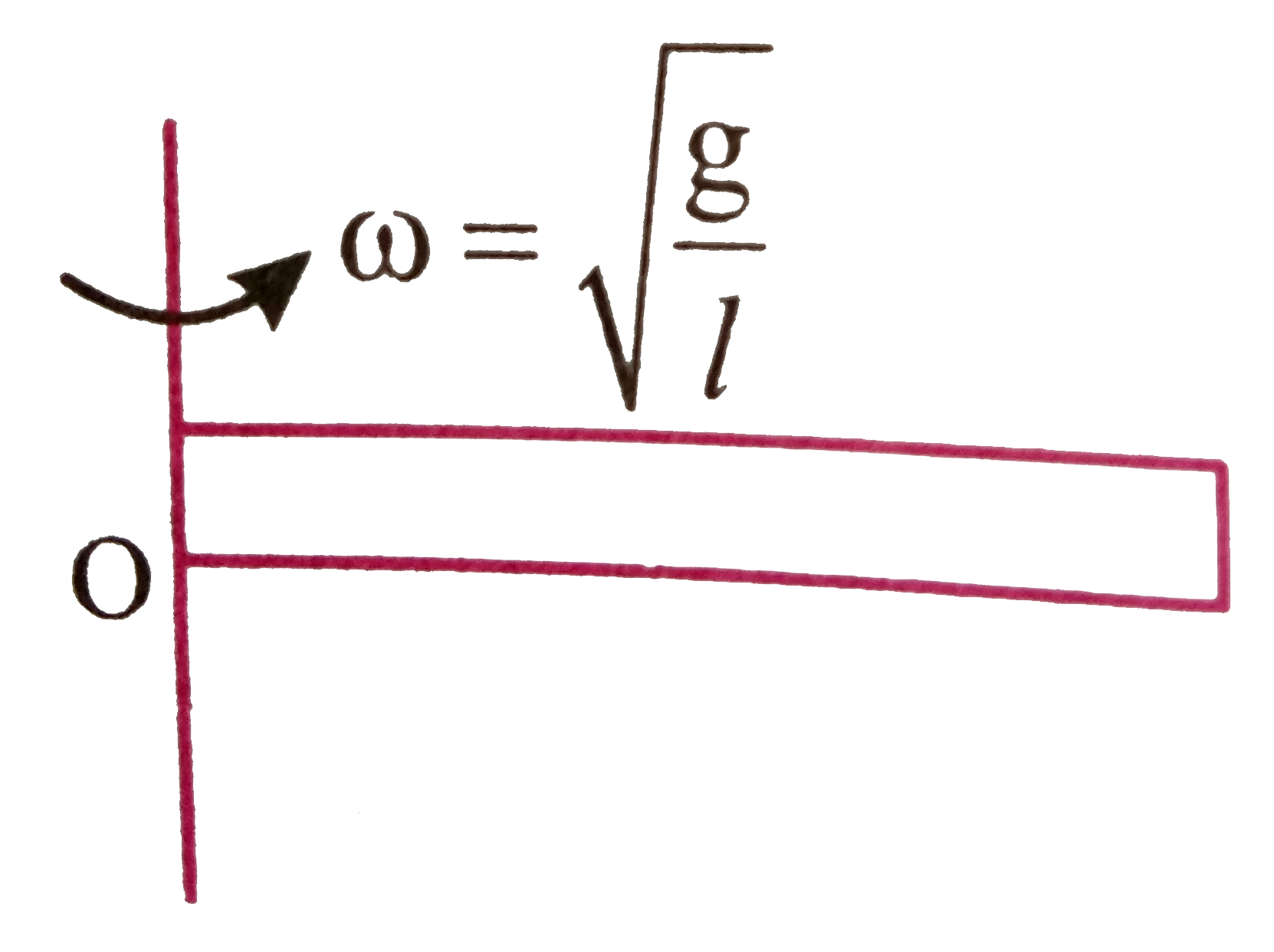
View SolutionThe torque `tau` on a body about a given point is found to be equal to AxxL where A is a constant vector, and L is the angular momentum of the body about that point. From this it follows that
View SolutionConsider a sphere of mass 'm' radius 'R' doing pure rolling motion on a rough surface having velocity `vec(v)_(0)` as shown in the figure. It makes an elastic impact with the smooth wall and moves back and starts rolling after some time again.

View SolutionIf a cylinder is rolling down the incline with sliding -
View Solutionwhich of the following statements are correct.
View SolutionA small particle of mass `m` is given an initial velocity `v_(0)` tangent to the horizontal rim of a smooth cone at a radius `r_(0)` from the vertical slides to point `B`, a vertical distance `h` below `A` and a distance `r` from the vertical centreline, its velocity `v` makes an angle `theta` with the horizontal tangent to the cone through `B`.
The value of `theta` is
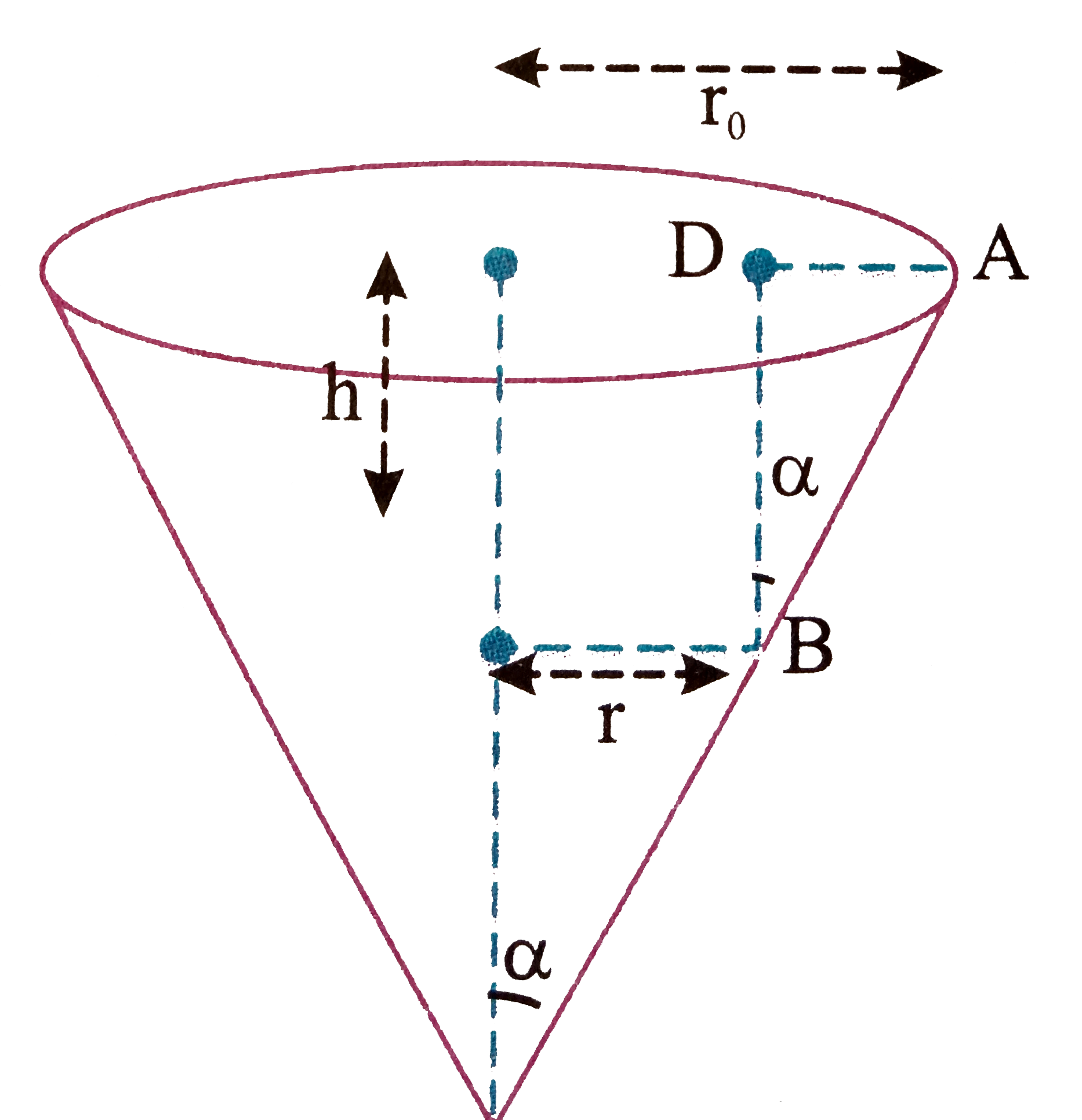
View SolutionA small particle of mass `m` is given an initial velocity `v_(0)` tangent to the horizontal rim of a smooth cone at a radius `r_(0)` from the vertical slides to point `B`, a vertical distance `h` below `A` and a distance `r` from the vertical centreline, its velocity `v` makes an angle `theta` with the horizontal tangent to the cone through `B`.
The speed of particle at point `B`

View SolutionA small particle of mass `m` is given an initial velocity `v_(0)` tangent to the horizontal rim of a smooth cone at a radius `r_(0)` from the vertical slides to point `B`, a vertical distance `h` below `A` and a distance `r` from the vertical centreline, its velocity `v` makes an angle `theta` with the horizontal tangent to the cone through `B`.
The minimum value of `v_(0)` for which particle will be moving in a horizontal circle of radius `r_(0)`.
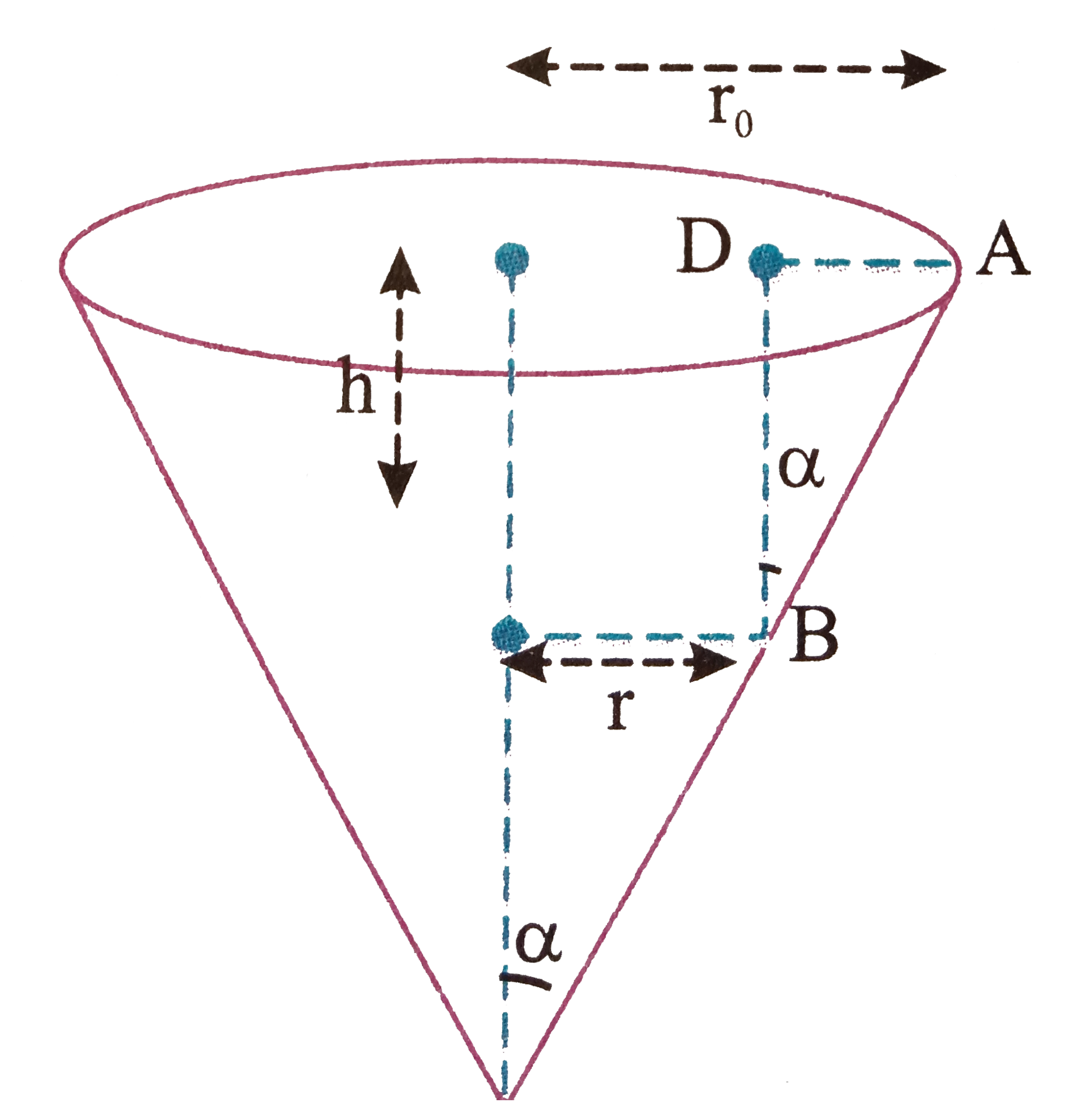
View SolutionA rod `AB` of mass `3m` and length `4a` is falling freely in a horizontal position and `c` is a point distance a from `A`. When the speed of the rod is `u`, the point `c` collides with a particle of mass `m` which is moving vertically upwards with speed `u`. if the impact between the particle and the rod is perfectely elastic find

The velocity of the particle immediately after the impact
View SolutionA rod `AB` of mass `3m` and length `4a` is falling freely in a horizontal position and `c` is a point distance a from `A`. When the speed of the rod is `u`, the point `c` collides with a particle of mass `m` which is moving vertically upwards with speed `u`. if the impact between the particle and the rod is perfectely elastic find
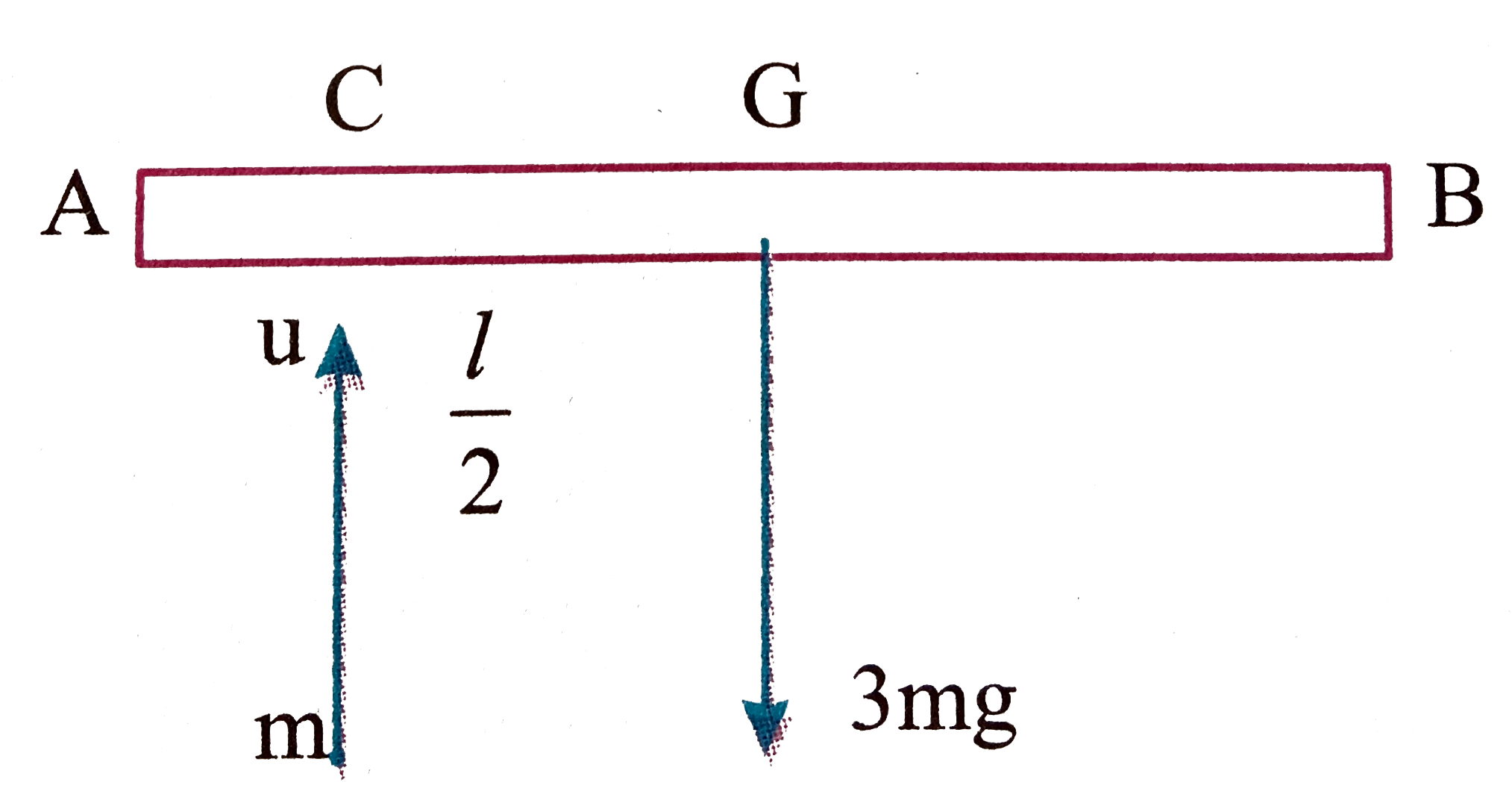
The angular velocity of the rod immediately after the impact
View SolutionA rod `AB` of mass `3m` and length `4a` is falling freely in a horizontal position and `c` is a point distance a from `A`. When the speed of the rod is `u`, the point `c` collides with a particle of mass `m` which is moving vertically upwards with speed `u`. if the impact between the particle and the rod is perfectely elastic find
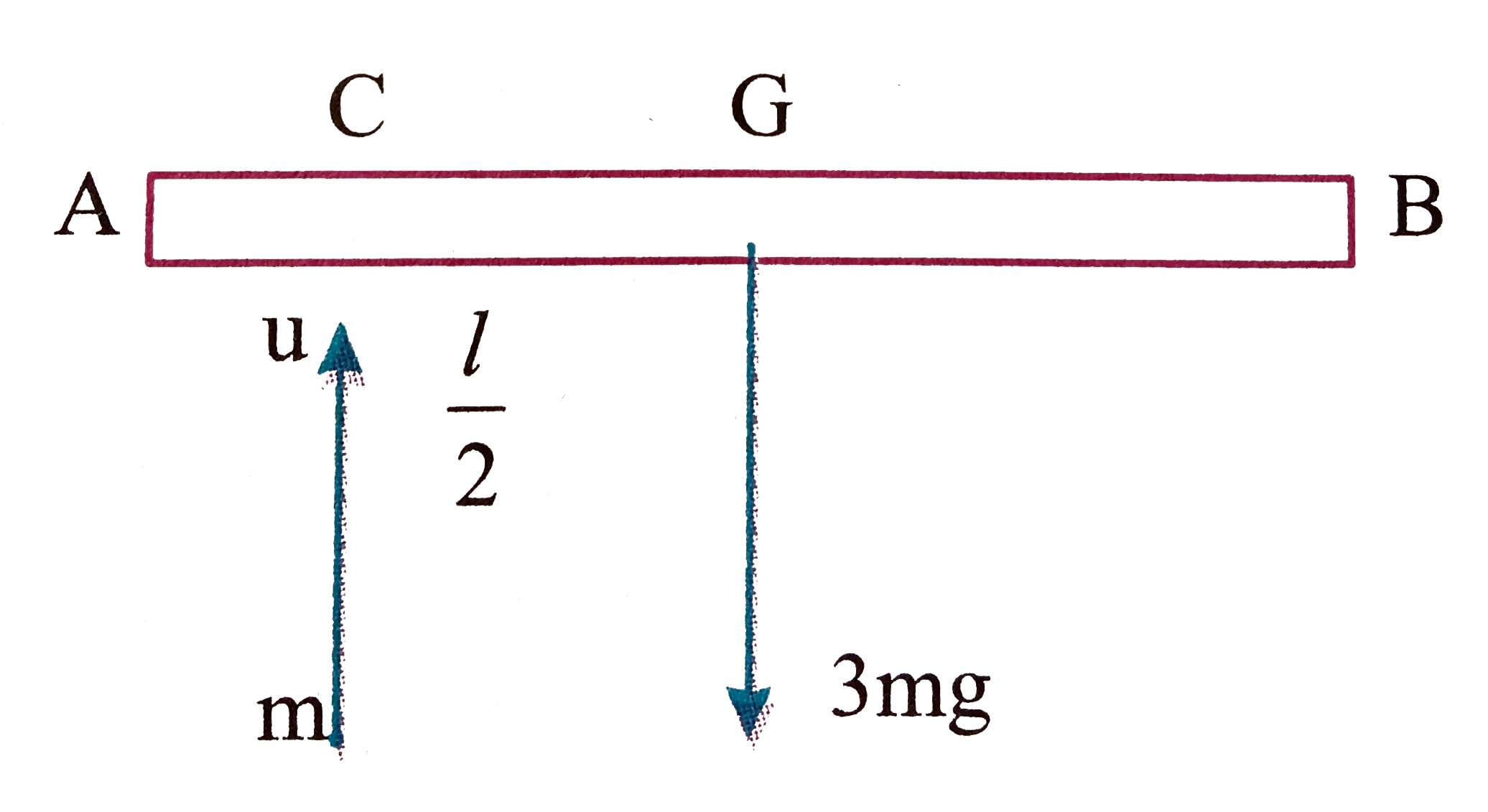
The speed of `B` immediately after the impact is
View SolutionAn uniform rod of mass `m=30 kg` and length `l=0.80 m` is free to rotate about a horizontal axis `O` passing through its centre. A particle `P` of mass `M=11.2 kg` falls vertically through a height `h=36/245 m` and collides elastically with the rod at a distance `l/4` from `O`. at the instant of collision the rod was stationary and was at angle `alpha=37^(@)` with horizontal as shown in figure
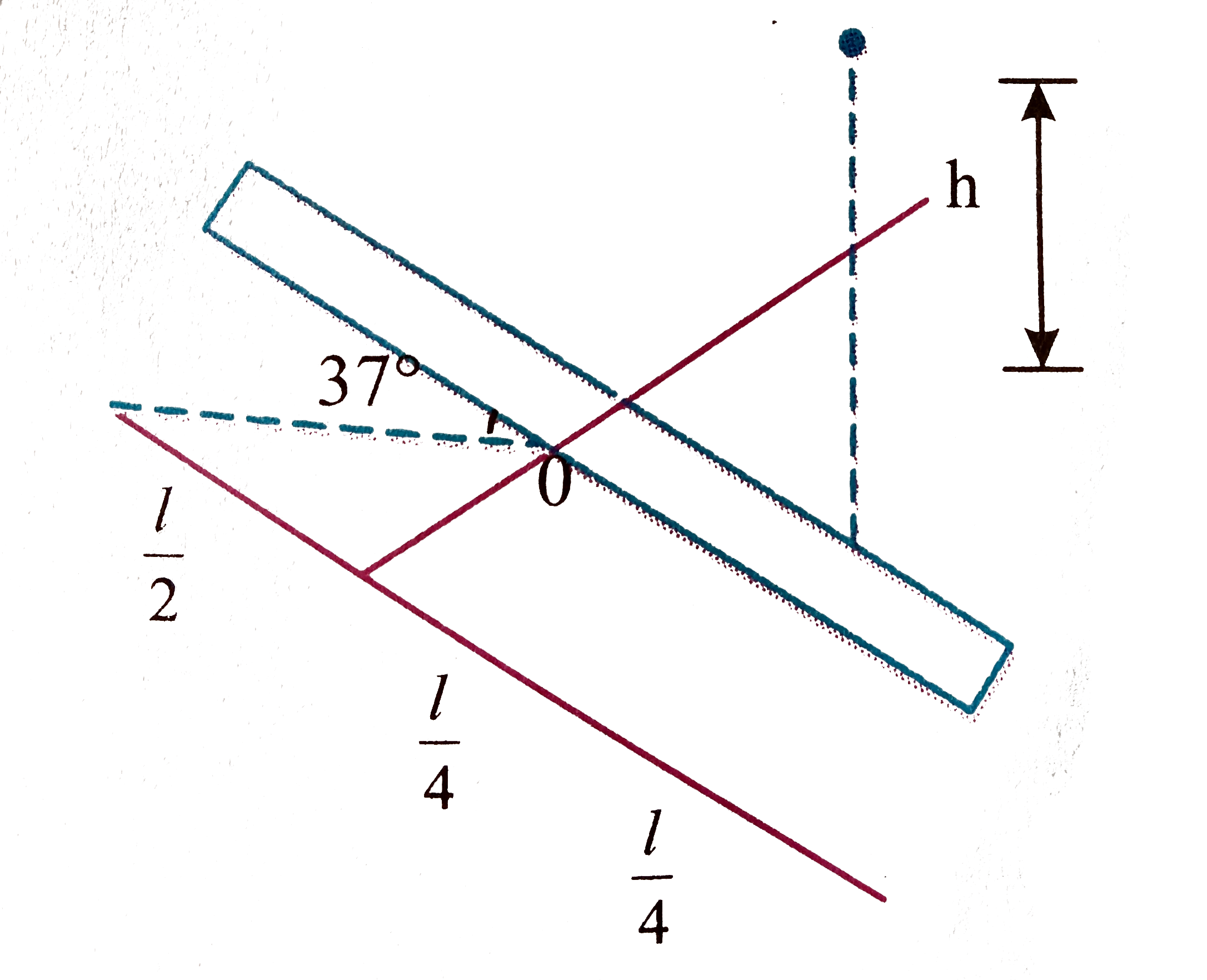
Calculate velocity of the rod just after collision is
View SolutionAn uniform rod of mass `m=30 kg` and length `l=0.80 m` is free to rotate about a horizontal axis `O` passing through its centre. A particle `P` of mass `M=11.2 kg` falls vertically through a height `h=36/245 m` and collides elastically with the rod at a distance `l/4` from `O`. at the instant of collision the rod was stationary and was at angle `alpha=37^(@)` with horizontal as shown in figure
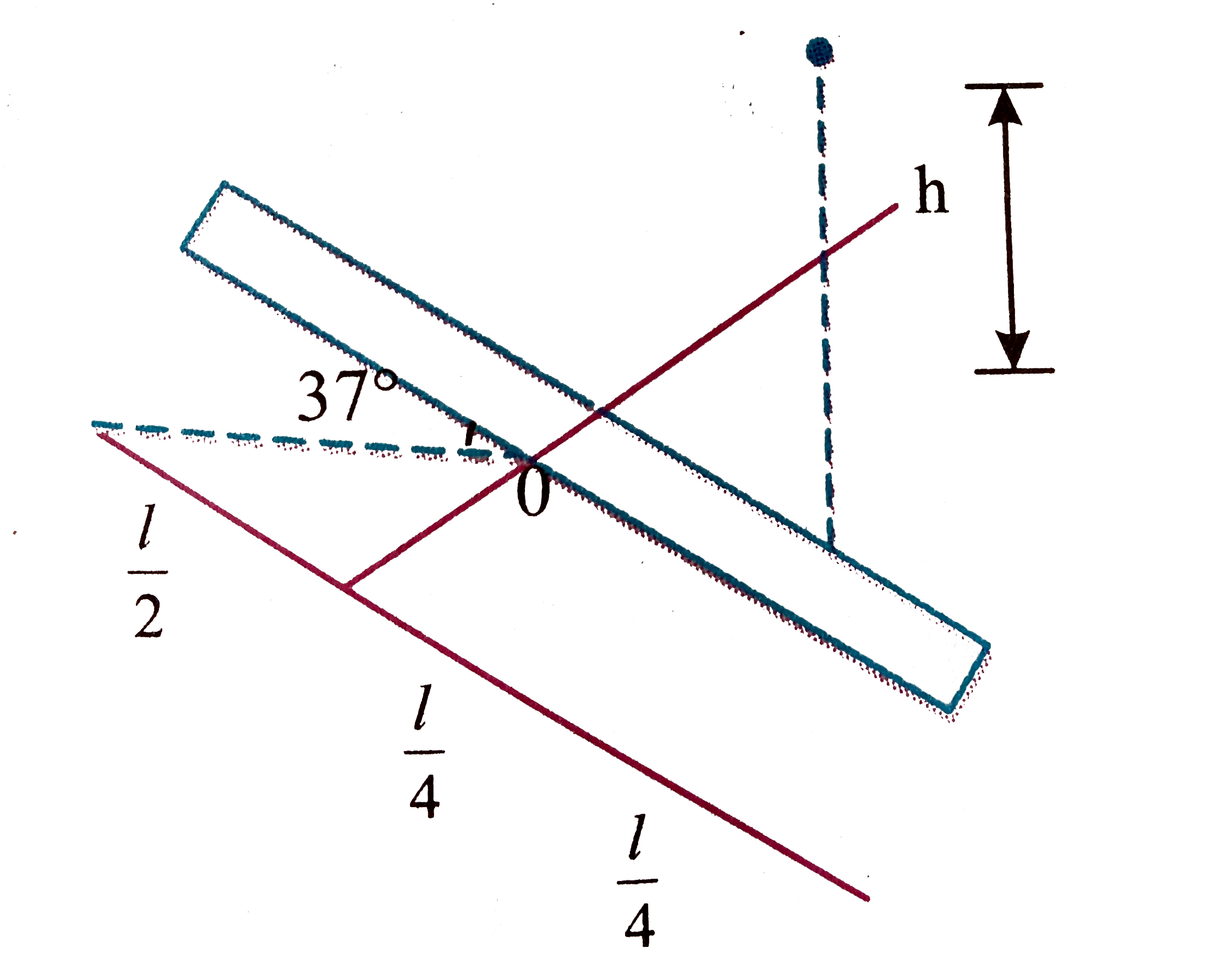
Velocity of particle `P` after collision `(g=10ms^(-2))`
View SolutionA uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity `vecV_0 = vacV_0hati.` The coefficinet of friction is `mu.`
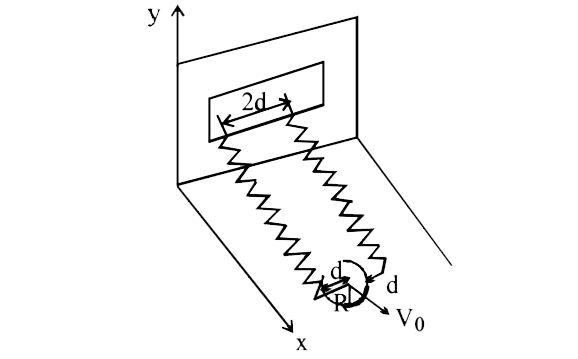
The net external force acting on the disk when its centre of mass is at displacement x with respect to its equilibrium position is.
View SolutionA uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity `vecV_0 = vacV_0hati.` The coefficinet of friction is `mu.`
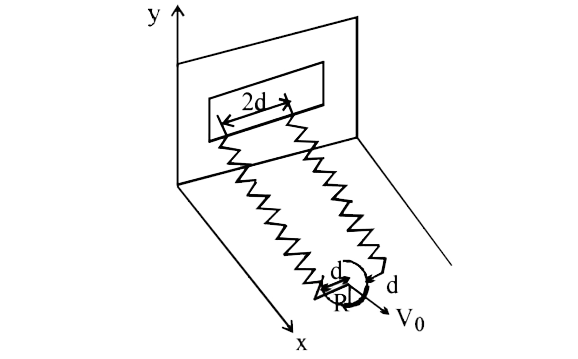
The centre of mass of the disk undergoes simple harmonic motion with angular frequency `omega` equal to -
View SolutionA uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity `vecV_0 = vacV_0hati.` The coefficinet of friction is `mu.`

The maximum value of `V_0` for whic the disk will roll without slipping is-
View SolutionA wheel of radius `R`, mass `m` with an axle of radius `r` is placed on a horizontal surface. Its moment of inertia is `I=mR^(2)`. Unwinding a rope from its axel a force `F` is applied to pull it along a horizontal surface. The friction is sufficient enough for its pure rolling `(angletheta=0^(@))`

Find the linear acceleration of the wheel
View SolutionA wheel of radius `R`, mass `m` with an axle of radius `r` is placed on a horizontal surface. Its moment of inertia is `I=mR^(2)`. Unwinding a rope from its axel a force `F` is applied to pull it along a horizontal surface. The friction is sufficient enough for its pure rolling `(angletheta=0^(@))`

Find the condition for which frictional force acts in backward direction
View SolutionA wheel of radius `R`, mass `m` with an axle of radius `r` is placed on a horizontal surface. Its moment of inertia is `I=mR^(2)`. Unwinding a rope from its axel a force `F` is applied to pull it along a horizontal surface. The friction is sufficient enough for its pure rolling `(angletheta=0^(@))`

Find the condition for which frictional force acts in forward direction
View SolutionConsider a cylinder of mass `M=1 kg` and radius `R=1 m`lying on a rough horizontal plane. It has a plank lying on its stop as shown in the figure.
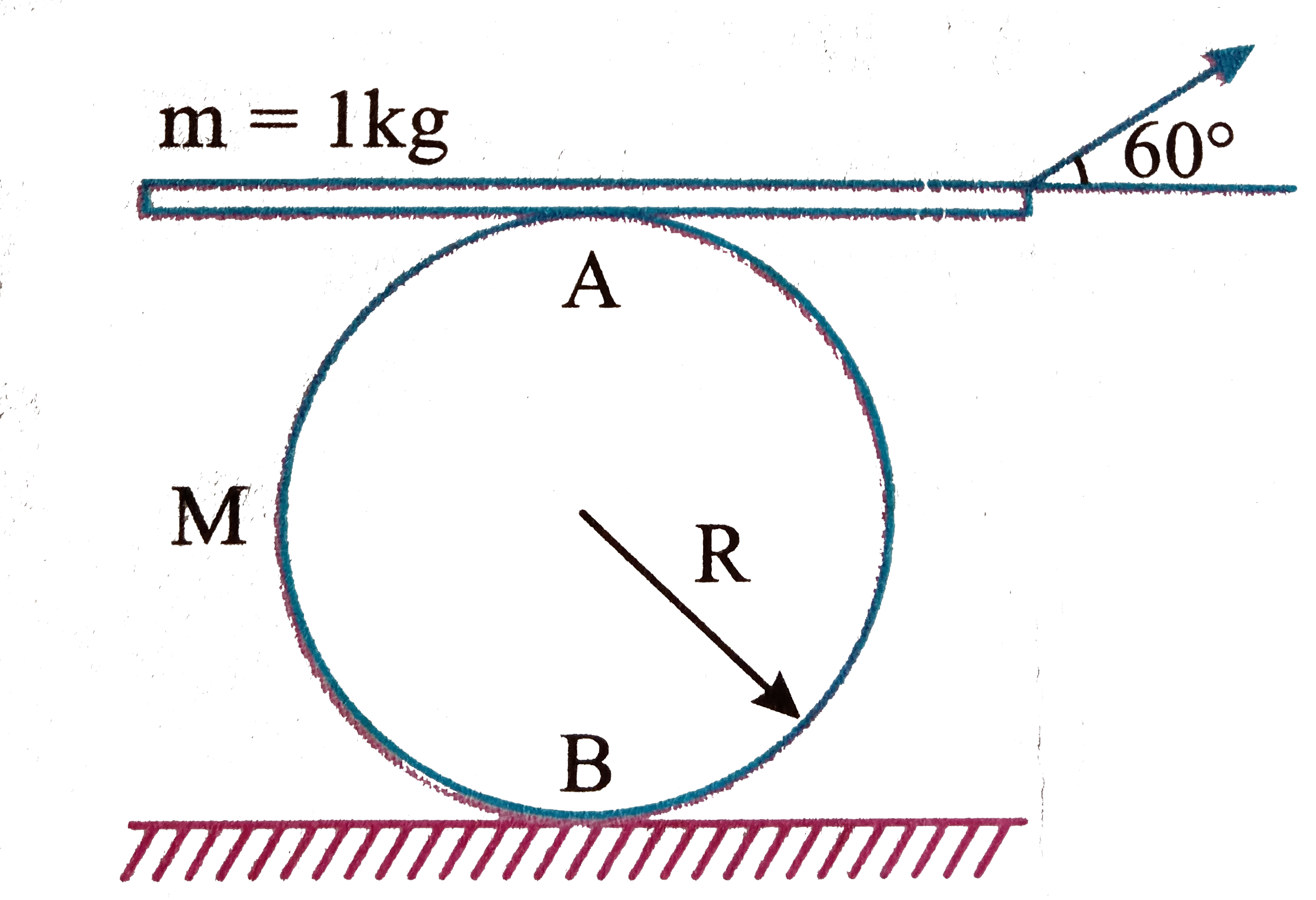
A force `F=55N` is applied on the plank moves and causes the cylinder to roll. The plank always remains horizontal. there is no slipping at any point of contact.
The acceleration of cylinder is
View SolutionConsider a cylinder of mass `M=1 kg` and radius `R=1 m`lying on a rough horizontal plane. It has a plank lying on its stop as shown in the figure.

A force `F=55N` is applied on the plank moves and causes the cylinder to roll. The plank always remains horizontal. there is no slipping at any point of contact.
The value of frictional force at `A` is
View SolutionConsider a cylinder of mass `M=1 kg` and radius `R=1 m`lying on a rough horizontal plane. It has a plank lying on its stop as shown in the figure.

A force `F=55N` is applied on the plank moves and causes the cylinder to roll. The plank always remains horizontal. there is no slipping at any point of contact.
The value of frictional force at `B` is
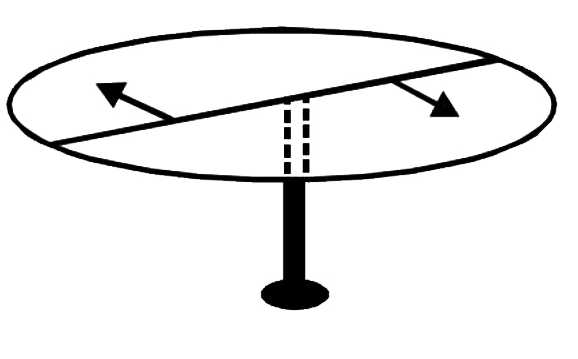
View SolutionA uniform rod is fixed to a rotating turntable so that its lower end is on the axis of the turntable and it makes an angle of `20 %` to the vertical. (The rod is thus rotating with uniform angular velocity about a vertical axis passing through one end.) If the turntable is rotating clockwise as seen from above.
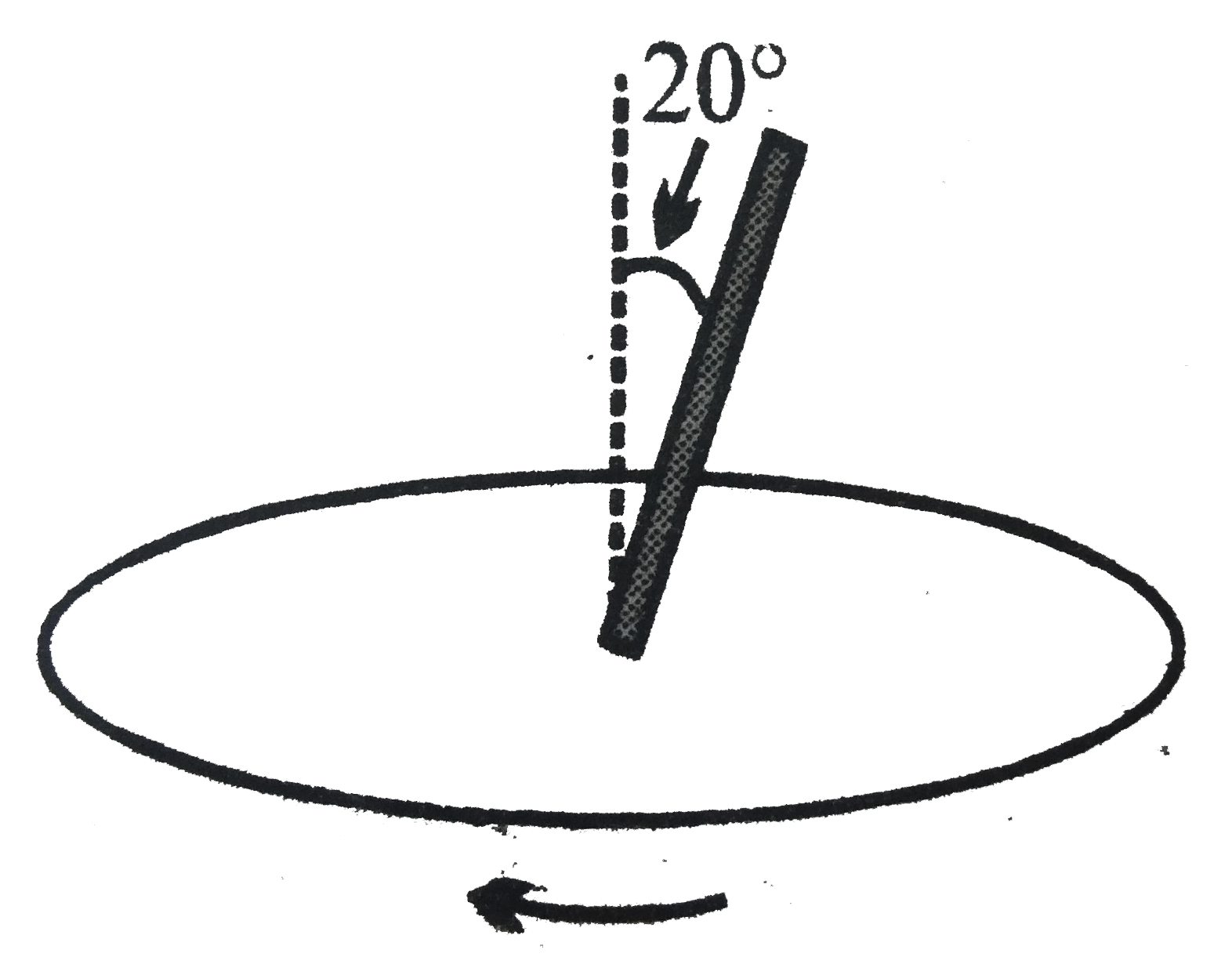 .
.
What is the direction of the rod's angular momentum vector (calculated about its lower end) ?
View SolutionA uniform rod is fixed to a rotating turntable so that its lower end is on the axis of the turntable and it makes an angle of `20 %` to the vertical. (The rod is thus rotating with uniform angular velocity about a vertical axis passing through one end.) If the turntable is rotating clockwise as seen from above.
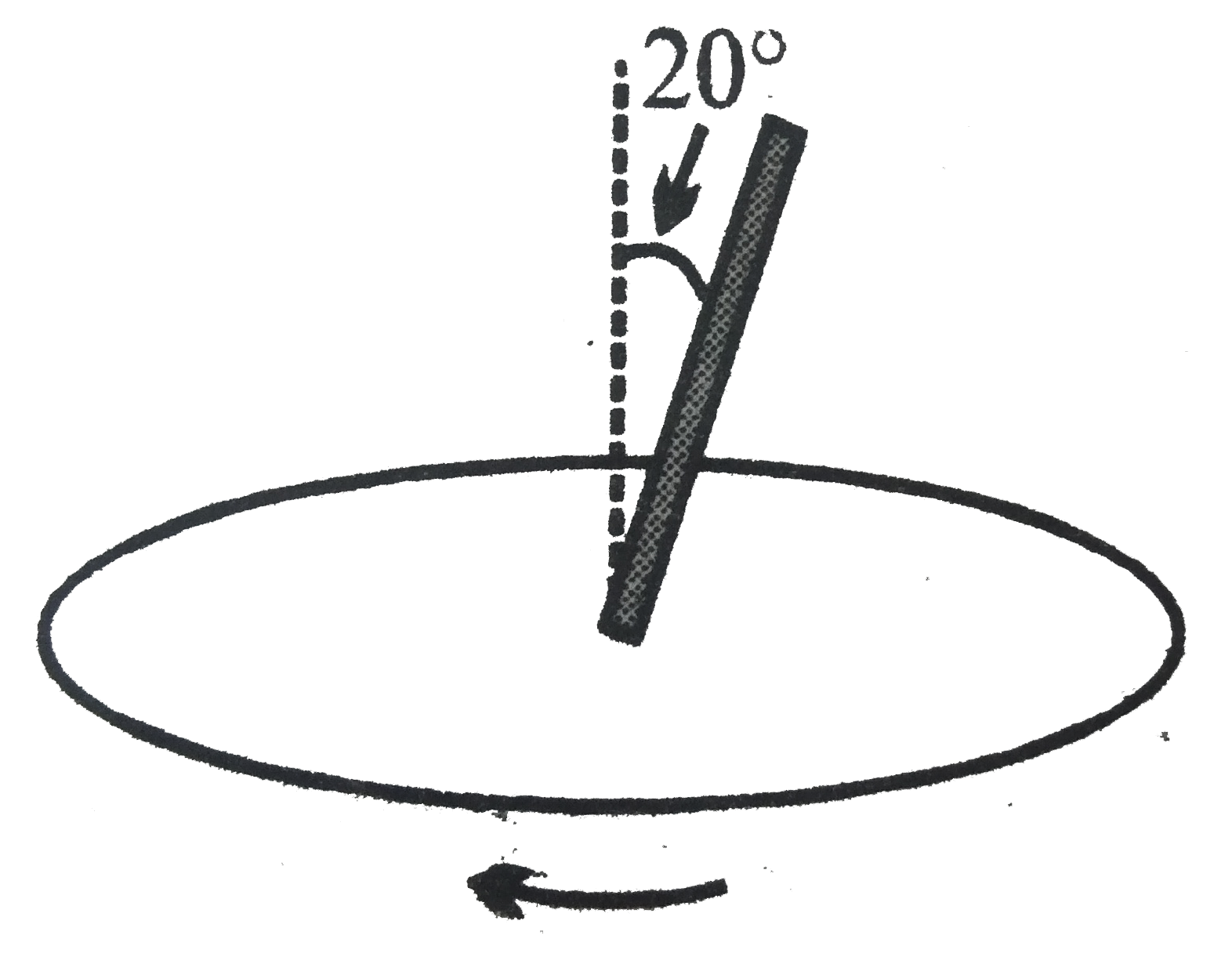 .
.
Is there a torque acts on it, and it so in what direction ?
View SolutionA disc of a mass `M` and radius `R` can rotate freely in vertical plane about a horizontal axis at `O`. Distant `r` from the centre of disc as shown in the figure. The disc is released from rest in the shown position.

The angular acceleration of disc when `OC` rotates by an angles of `37^(@)` is
View SolutionA disc of mass `M` and radius `R` can rotate freely in a vertical plane about a horizontal axis at `O` distance `r` from the centre of the disc as shown in Fig. The disc is released from rest in the shown position. Answer the following questions based on the above information
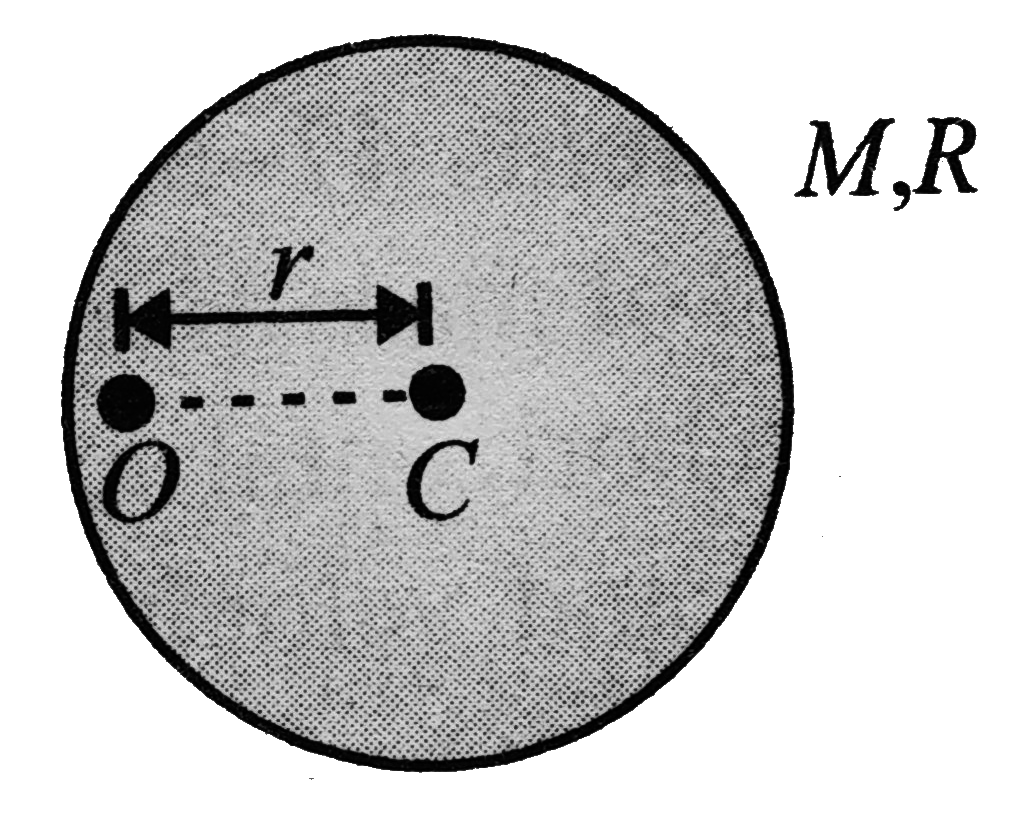
The angular velocity of the disc when `OC` rotates by an angle of `37^@`
View SolutionA disc of mass `M` and radius `R` can rotate freely in a vertical plane about a horizontal axis at `O` distance `r` from the centre of the disc as shown in Fig. The disc is released from rest in the shown position. Answer the following questions based on the above information

Reaction force exerted by the hinge on the disc at the instant when disc rotates by an angle of `37^@`is
View SolutionA plank of mass `m_(1)` with a uniform solid sphere of mass `m_(2)` placed on it rests and a force `F` is applied to the plank. The acceleration of the plank provided there is no sliding between the plank and the sphere is `(F/(m_(1)+n/7m_(2)))` then the value of `n` is

View SolutionA uniform cylinder of radius `R` is spinned about it axis to the angular velocity `omega_(0)` and then placed into a corner,. The coeficient of friction between the corner walls and the cylinder is `mu_(k)` How many turns will the cylinder accomplish before it stops?

View SolutionThe pulley shown in figure has a radius 10 cm and moment of inertia 0.5 kg-m^2 about its axis. Assuming the inclined planes to be frictionless, calculate the acceleration of the 4.0 kg block.
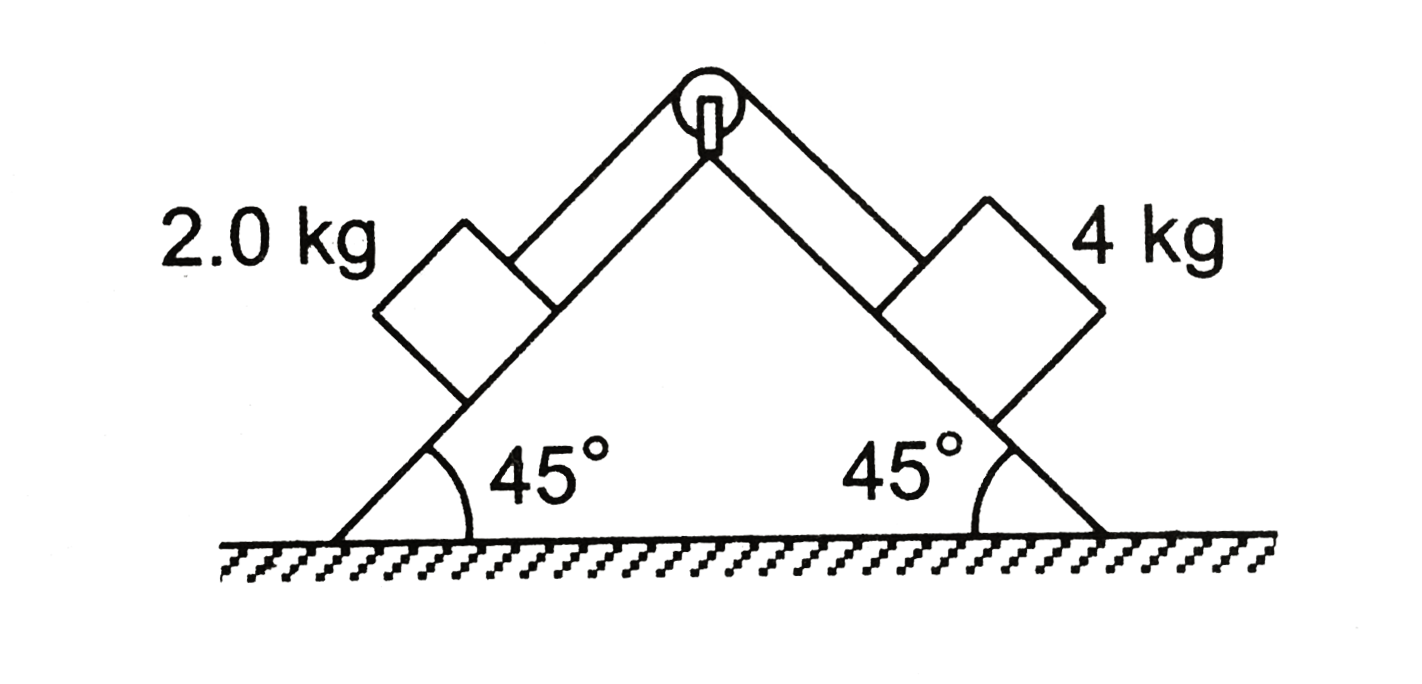
View SolutionTwo solid semi-circular disks fo equal masses `m=10 kg` collide and stick together. Their initial velocities are shown initially not rotating. The combined object is a circular disk of radius `0.1 m` it is spinning with an angular velocity `omega=10rad//s`. how much mechanical energy (in `J`) is lost in collision ?

View SolutionA ball of radius `R=20 cm` has mass `m=0.75 kg` and moment of inertia (about its diameter) `I=0.0125 kg m^(2)`. The balls rolls with velocity `V_(0)=10 ms^(-1)` towards a smooth vertical wall. If coefficient of restitution between the wall and the ball is `e=0.7`, velocity `V` of the ball after the collision is `(g=0ms^(-2))`
View SolutionA uniform square plate of mass 'm'is supported as shown. If the cable suddenly breaks, assuming centre of mass is on horizontal line passing through `A` determine, the reaction at `A` is `(mg)/n` that `n` is
View SolutionIn the figure shown there is a fixed wedge 'W' of inclination `theta`. `A` is a block, `B` is a disc and 'C' is a solid cylinder. `A,B,C` each has mass 'm'. Assuming there is no sliding anywhere and string to be of negligible mass find :
The fricition force acting on the cylinder due to the wedge is `(mg)/15(1+n sin theta)` that `n` is
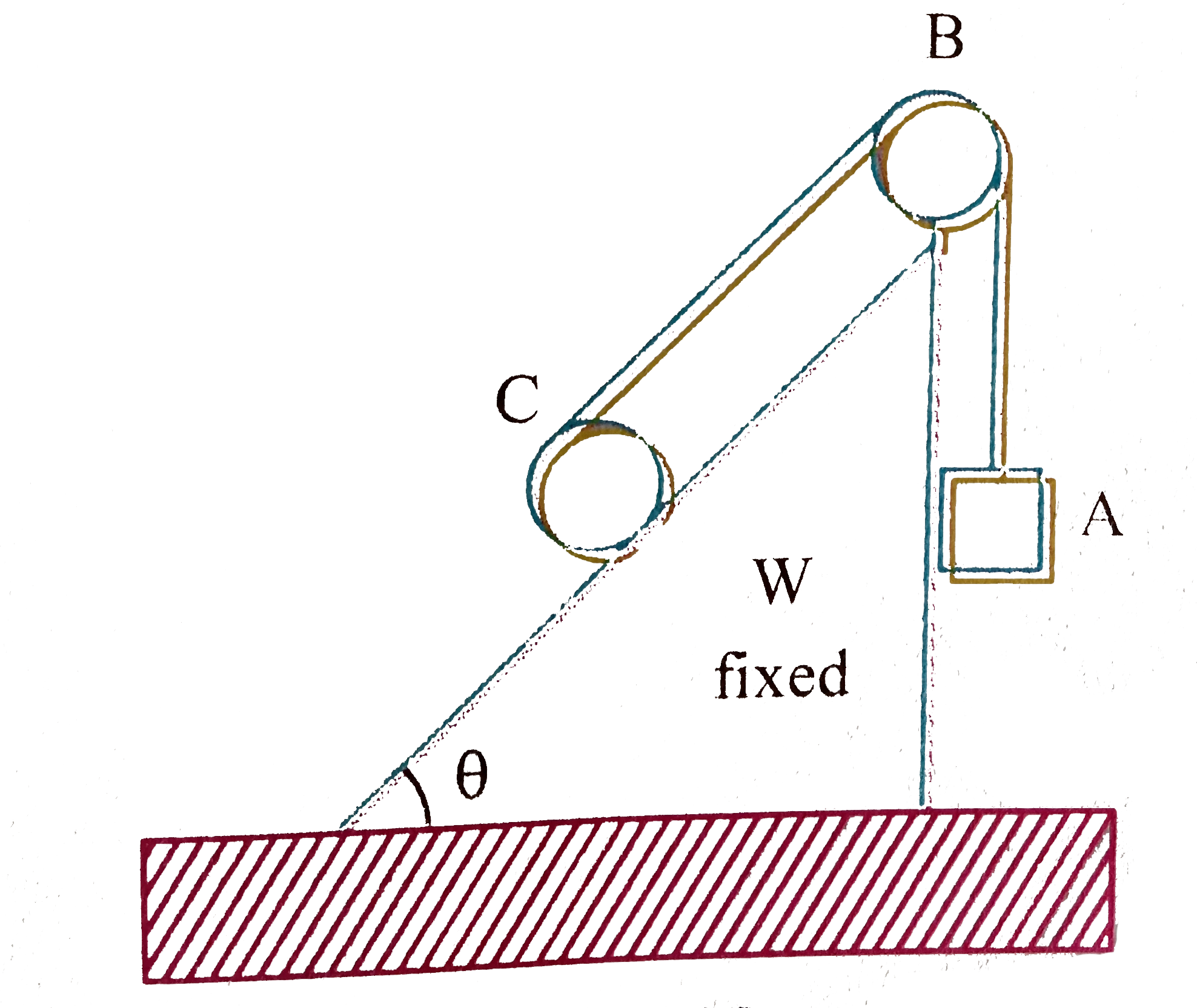
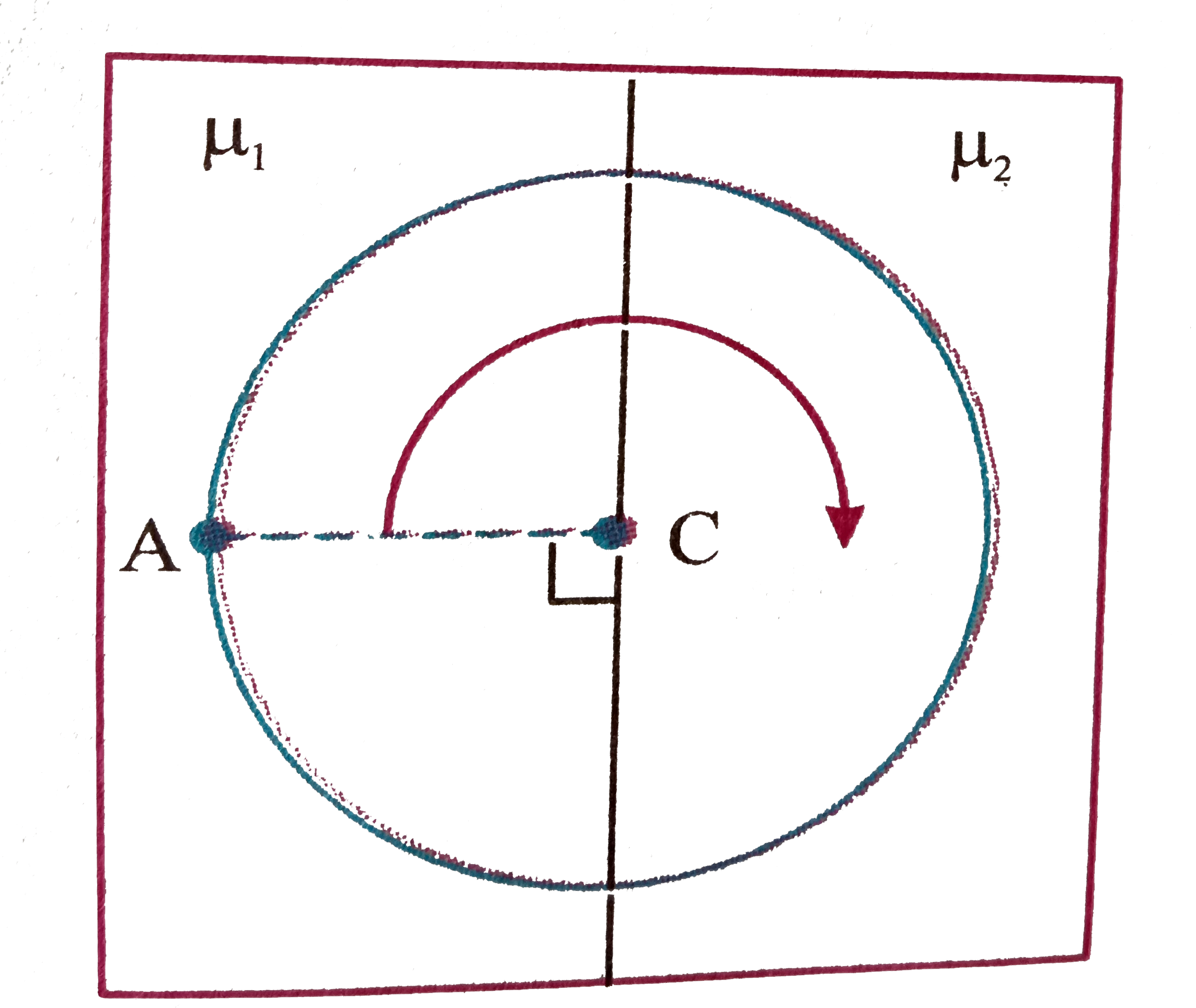
View SolutionIn the figure shown a uniform ringh of mass `m` placed on arough horizontal fixed surface. The coefficient of friction between left half of ring and table is `mu_(1)` whereas between right half and table is `mu_(2)` at the moment shown. The ring has angular velocity in clockwise sence in the figure shown. at this moment find the magnitude of acceleration ( in `m//s^(2)`) of centre `C` of ringe. [Given `g=10 m//s^(2)`]
View SolutionA thin rod of mass `m` and length `2l` is placed horizontally and perpendicular to a horizontal rough nail, as shown in figure and set free. The point of contanct of the rod with the nails is `l//3` distance away form the centre of rod. If the rod starts slipping when it forms an angle `theta` with the horizontal and the coefficient of friction of rod with nails is `mu`, then find `(mu)/(tan theta)`.

View SolutionFigure shows an arrangements of masses hanging from a ceilling. In equilibrium each rod is horizontal, has negligible mass and extends three times as far to the right of the wire supporting is as to the left. If mass `m_(4)` is `48 kg,` then `(m_(3))/(m_(2))` is
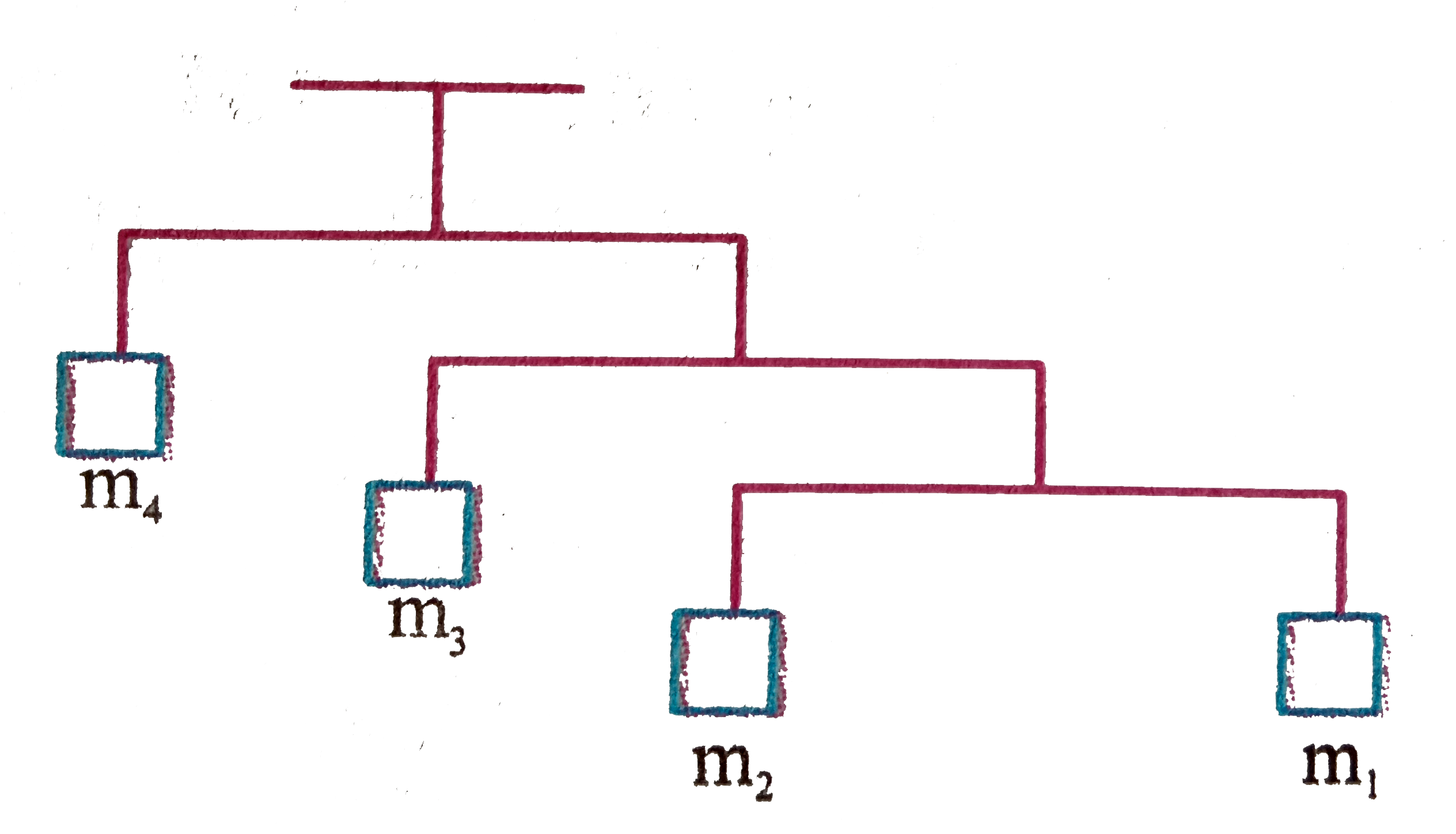
View SolutionA right triangular plate `ABC` of mas `m` is free to rotate in the vertical plane about a fixed horizontal axis through `A`. It is supported by a string such that the side `AB` is horizontal. The reaction at the support `A` is :
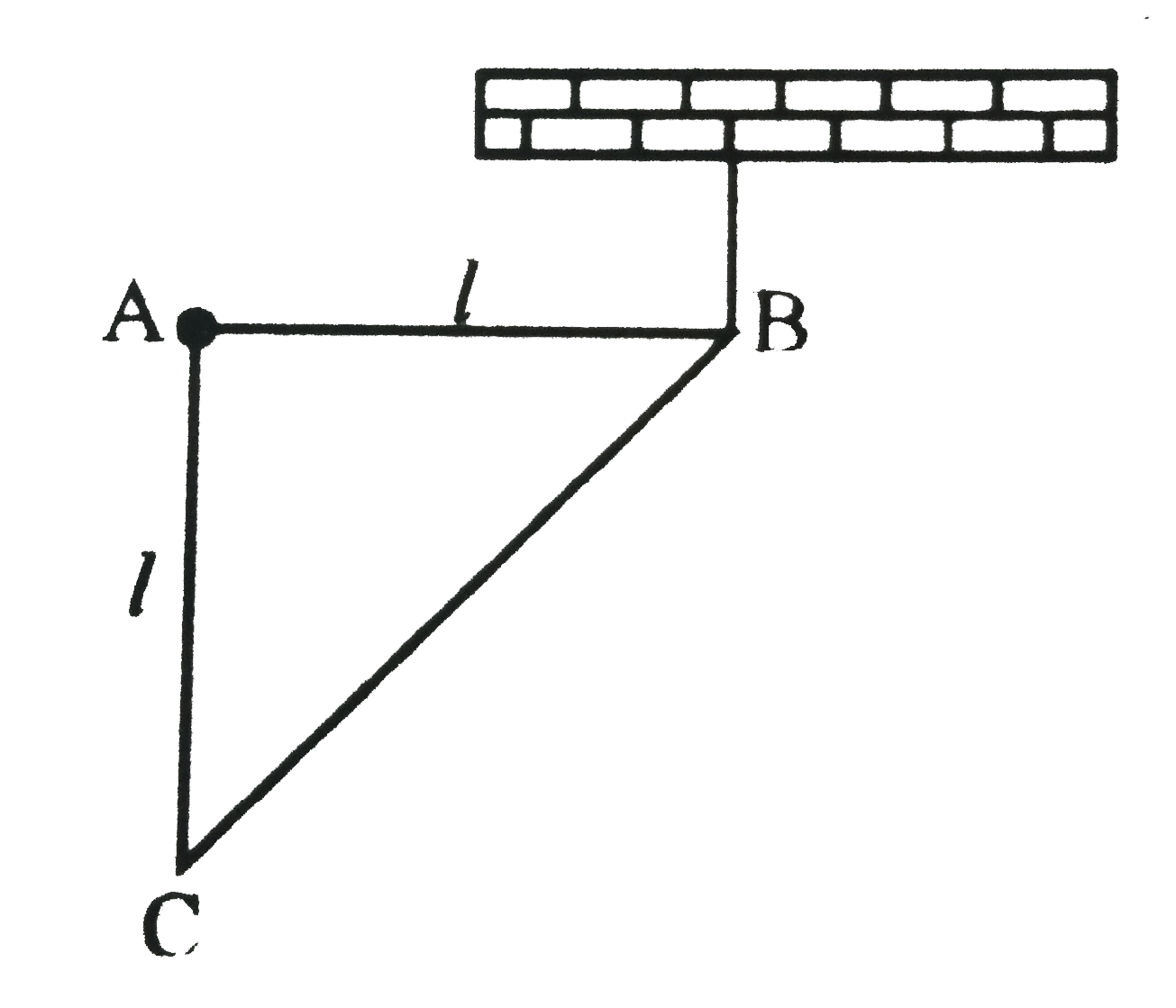 .
.
View SolutionThe densitis of two solid spheres A and B of the same radii R very with radial distance `r as p_A(r ) = k ((r )/(R )) and p_B(r ) = k((r )/(R )^5,` respectively, where k is a constant . The moments of inertia of the inividual spheres about axes passing throgh their centres are `I_A and I_B` respectively. if `(I_B)/(I_A) = (n)/(10),` the value of n is
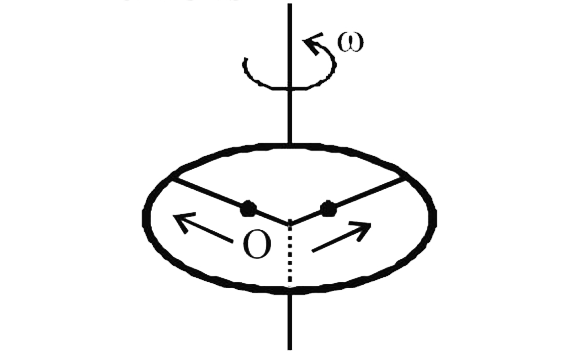
View SolutionA horizontal circular platform of radius 0.5 m and mass axis. Two massless spring toy-guns, each carrying a steel ball of mass 0.05 kg are attached to the platform at a distance 0.25m from the centre on its either sides along its diameter (see figure). Each gun simultaneously fires the balls horizontally and perpendicular to the diameter in opposite directions. After leaving the platform, the balls have horizontal speed of `9ms^(-1)` with respect to the ground. The rotational speed of the platform in `rad s^(-1)` after the balls leace the platform is
View SolutionA ring of mass M and radius R is rotating with angular speed `omega` about a fixed vertical axis passing through its centre O with two point masses each of mass `(M)/(8)` at rest at O. These masses can move radially outwards along two massless rods fixed on the ring as shown in the figure. At some instant the angular speed of the system is `(8)/(9) omega` and one fo the masses is at a distance of `(3)/(5) R` from O. At this instant the distance of the other mass from O is
View Solution
Level-VI questions and complete solutions for chapter SYSTEM OF PARTICLES of NARAYANA PHYSICS (HINGLISH) of Class 11