Complete Solutions to Level -I(H.W) of chapter SYSTEM OF PARTICLES of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SYSTEM OF PARTICLES |
| NARAYANA | Level -I(H.W) |
| Number Of Questions | 58 |
| Academic Year | 2023-24 |
The distance of centre of mass from `O` is
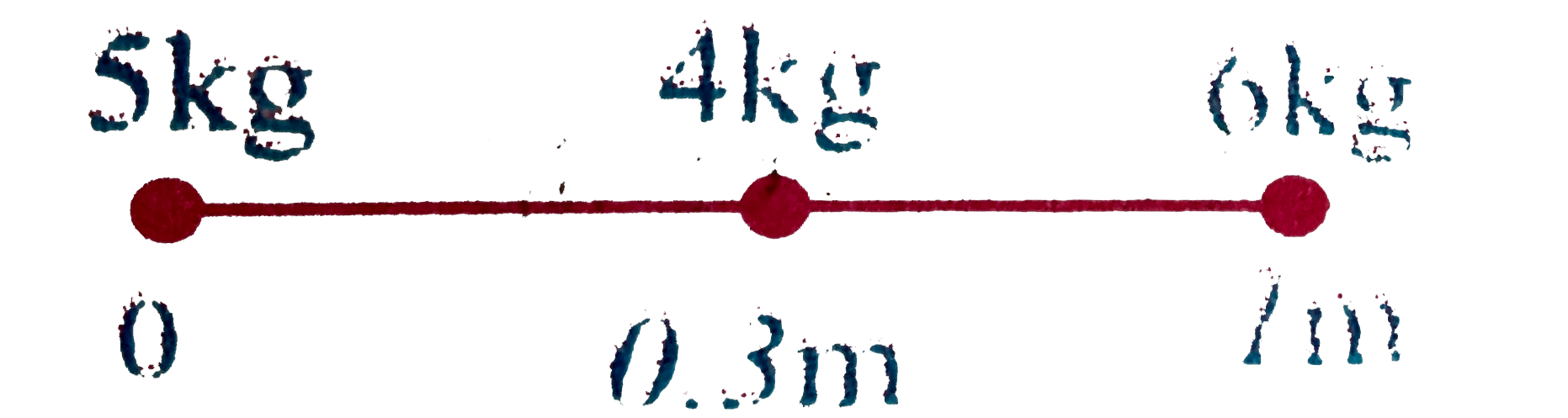
View SolutionFour bodies of masses `1,2,3,4 kg` respectively are placed at the comers of a square of side `a`. Coordinates of centre of mass are (take `1kg` at the origin,`2kg` on X-axis and `4kg` on Y-axis)
View SolutionA uniform rod o length one meter is bent at its midpoint to make `90^@`. The distance of centre of mass from the centre of rod is (in `cm`)
View SolutionParticles of masses `1kg` and `3kg` are at `2i + 5j + 13k)m` and `(-6i + 4j - 2k)m` then instantaneous position of their centre of mass is
View SolutionA boat of mass `50kg` is at rest. A dog of mass `5kg` moves in the boat with a velocity of `20m//s`. What is the velocity of boat?
View SolutionTwo bodies of masses `5kg` and `3kg` are moving towards each other with `2ms^(-1)` and `4ms^(-1)` respectively. Then velocity of centre of mass is
View SolutionA circular disc of radius `20cm` is cut from one edge of a larger circular disc of radius `50cm`. The shift of centre of mass is
View SolutionTwo particles of masses `4kg` and 6kg` are separated by a distance of `20cm` and are moving towards each other under mutual force of attraction, the position of the point where they meet is
View SolutionA uniform metre rod is bent into `L` shape with the bent arms at `90^@` to each other. The distance of the centre of mass from the bent point is
View SolutionTwo objects of masses `200g` and `500g` have velocities of `10i m//s` and `(3i + 5j) m//s` respectively. The velocity of their centre of mass is
View SolutionThe position of a particle is given by `vec r = hat i + 2hat j - hat k` and its momentum is `vec p = 3 hat i + 4 hat j - 2 hat k`. The angular momentum is perpendicular to
View SolutionA uniform sphere has radius `R`. A sphere of diameter `R` is cut from its edge as shown. Then the distance of centre of mass of remaining portion from the centre of mass of the original sphere is

View SolutionThe are of the parallelogram whose adjacent sides are `P=3hat i + 4 hat j, Q = -5 hat i + 7hat j` is (in sq. units)
View SolutionIf `vec A= 3i + j +2k` and `vec B = 2i - 2j +4k` and `theta` is the angle between the two vectors, then `sin theta` is equal to
View SolutionA particle is moving with uniform speed `0.5 m//s` along a circle of radius `1m` then the angular velocity of particle is (in `rad s^(-1)`)
View SolutionThe angular velocity of the seconds hand in a watch is
View SolutionThe angular displacement of a particle is given by `theta = t^3 + 2t +1`, where `t` is time in seconds. Its angular acceleration at `t=2s` is
View SolutionA circular disc is rotating about its own axis at a uniform angular velocity `omega`. The disc is subjected to uniform angular retardation by which its angular velocity is decreased to `omega/2` during `120` rotations. The number of rotations further made by it before coming to rest is
View SolutionThe handle of a door is at a distance `40cm` from axis of rotation. If a force `5N` is applied on the handle in a direction `30^@` with plane of door, then the torque is
View SolutionA door can just be opened with `10N` force on the handle of the door. The handle is at a distance of `50cm` from the hinges. Then, the torque applied on the door (in `Nm`) is
View SolutionA particle of mass m is projected with speed u at an angle `theta` with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View SolutionA uniform rod is `4m` long and weights `10kg`. If it is supported on a kinetic edge at one meter from the end, what weight placed at that end keeps the rod horizontal.
View SolutionThe ratio of moments of inertia of solid sphere about axes passing through its centre and tangent respectively is
View SolutionIf `I` moment of inertia of a thin circular plate about an axis passing through tangent of plate in its plane. The moment of inertia of same circular plate about an axis perpendicular to its plane and passing through its centre is
View SolutionThe moment of inertia of a solid sphere about an axis passing through its centre is `0.8kgm^2`. The moment of inertia of another solid sphere whose mass is same as mass of first sphere, but the density is `8` times density of first sphere, about an axis passing through its centre is
View SolutionMoment of inertia of a hoop suspended from a peg about the peg is
View SolutionFour particles each of mass `1kg` are at the four corners of square of side `1m`. The M.I. of the system about a normal axis through centre of square is
View SolutionThree identical masses, each of mass `1kg,` are placed at the corners of an equilateral triangle of side `l`. Then the moment of inertia of this system about an axis along one side of the triangle is
View SolutionA wire of mass `m` and length `l` is bent in the form of circular ring. The moment of inertia of the ring about its axis is
View SolutionThe moment of inertia of a thin uniform rod of mass `M` and length `L` about an axis perpendicular to the rod, through its centre is `I`. The moment of inertia of the rod about an axis perpendicular to rod through its end point is
View SolutionFour point size bodies each of mass `m` are fixed at four corners of light square frame of side length `1m`. The radius of gyration of these four bodies about an axis perpendicular to the plane of frame passing through its centre is
View SolutionUniform square plate of mass `240` gram is made to rotate about an axis passing through any diagonal of plate. If its moment of inertia is `2xx10^(-4) kgm^2` then its side length is
View SolutionTwo objects of masses `1kg` and `2kg` separated by a distance of `1.2m` are rotating about their centre of mass. Find the moment of inertia of the system
View SolutionThe radius of gyration of a body about an axis at a distance of `4cm` from its centre of mass is `5cm`. The radius of gyration about a parallel axis through centre of mass is
View SolutionThe M.I. of a thin rod about a normal axis through its centre is `I`. It is bent at the centre suh that the two parts are perpendicular to each other and perpendicular to the axis. The M.I. Of the sytem about the same axis will be
View SolutionThe moment of inertia of two spheres of equal masses about their diameters are the same. One is hollow, then ratio of their diameters
View SolutionA circular disc of mass `4kg` and of radius `10cm` is rotating about its natural axis at the rate of `5 rad//sec`. Its angular momentum is
View SolutionIf the mass of earth and radius suddenly become `2` times and `1//4th` of the present value, the length of the day becomes
View SolutionA child is standing with folded hands at the center of a platform rotating about its central axis. The kinetic energy of the system is `K`. The child now stretches his arms so that the moment of inertia of the system doubles. The kinetic energy of the system now is
View SolutionIf radus of earth shrinks by `0.1%` without change in its mass, the percentage change in the duration of one day
View SolutionA ballet dancer spins about a vertical axis at 60 rpm with his arms closed. Now he stretches his arms such that M.I. Increases by `50%`. The new speed of revolution is
View SolutionA metallic circular wheel is rotating about its own axis without friction. If the radius of wheel expands by `0.2%`, percentage change in its angular velocity
View SolutionA uniform circular disc of radius `R` is rotating about its own axis with moment of inertia `I` at an angular velocity `omega` if a denser particle of mass `m` is gently attached to the rim of disc than its angular velocity is
View SolutionA particle of mass `m` is moving in a plane along a circular path of radius `r`. Its angular momentum about the axis of rotation is `L`. The centripetal force acting on the particle is.
View Solution`vecF = a hat i + 3hat j+ 6 hat k` and `vec r = 2hat i-6hat j -12 hat k`. The value of `a` for which the angular momentum is conserved is
View SolutionWhat will be the duration of the day, if the earth suddenly shrinks to `1//64 th` of its original volume, mass remaining unchenged ?
View SolutionA mass is whirled in a circular path with an angular momentum `L`. If the length of string is now halved keeping the angular velocity same, the new angular momentum is
View SolutionA disc rotates with angular velocity `omega` and kinetic energy `E`. Then its angular momentum
View SolutionA wheel at rest has M.I. `2/(pi^2) kgm^2`. It is rotated by a `60W` motor for one minute. The number of rotations made by the wheel in one minute is
View SolutionThe shaft of a motor is making 1260rpm. The torque supplied by the motor is `100Nm`. The power of motor is (in `KW`)
View SolutionAn electric motor rotates a wheel at a constant angular velocity `10rps` while opposing torque is `10Nm`. The power of that electric motor is
View SolutionThe work done in increasing the angular frequency of a circular ring of mass `2kg` and radius `25cm` from 10rpm to 20rpm about is axis
View SolutionA ring is allowed to roll down on an incline of `1` in `10` without slipping. The acceleration of its centre of mass is
View SolutionA cylinder is released from rest from the top of an incline of inclination `theta` and length `l`. If the cylinder roles without slipping, its speed at the bottom
View SolutionFor a body rolling along a level surface, without slipping the translational and rotational kinetic energies are in the ratio `2:1`. The body is
View SolutionA solid sphere and a spherical shell roll down an incline from rest from same height. The ratio of times taken by them is
View SolutionWhen a solid sphere is rolling along level surface the percentage of its total kinetic energy that is translational is
View SolutionA thin ring of mass `1kg` and radius `1m` is rolling at a speed of `1ms^(-1)`. Its kinetic energy is
View Solution
Level -I(H.W) questions and complete solutions for chapter SYSTEM OF PARTICLES of NARAYANA PHYSICS (HINGLISH) of Class 11