Complete Solutions to MULTIPLE CHOICE QUESTIONS of chapter GRAVIATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | GRAVIATION |
| PRADEEP | MULTIPLE CHOICE QUESTIONS |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Two satellite of mass `m` and `9 m` are orbiting a planet in orbits of radius `R`. Their periods of revolution will be in the ratio of
View SolutionThe value of `g` at a particular point is `10 m s^(-2)`. Suppose the earth shrinks uniformly to half of its present size without losing any mass. The value of `g` at the same point (assuming that the distance of the point from the centre of the earth does not change) will now be
View SolutionRead the following statements :
`S_(1)` : An object shall weigh more at pole than at equator when weighed by using a physical balance.
`S_(2)` : It shall weigh the same at pole and equator when weighed by using a physical balance.
`S_(3)` : It shall weigh the same at pole and equator when weighed by using a spring balance.
`S_(4)` : It shall weigh more at the pole than at equator when weighed using a spring balance.
Which of the above statements is/are correct ?
View SolutionThe height at which the acceleration due to gravity becomes `(g)/(9)` (where g =the acceleration due to gravity on the surface of the earth) in terms of R, the radius of the earth, is :
View SolutionEnergy required to move a body of mass m from an orbit of radius 2R to 3R is
View SolutionA man standing on an international space sattion, which is orbiting earth at an altitude `520 km` with a constant speed `7.6 km//s`. If the man's weight is `50 kg`, this acceleration is (radius of earth is `6400 km` and value of `g` on earth is `9.8 m//s^(2))`.
View SolutionThe acceleration due to gravity at a height `1km` above the earth is the same as at a depth `d` below the surface of earth. Then :
View SolutionIf `g` denotes the value of acceleration due to gravity at a point distance `r` from the centre of earth of radius `R`. If `r lt R`, then
View SolutionThe time period of a sceond's pendulum in a satellite is
View SolutionStatement-1 : The escape velocity from the earth is `upsilon_(e)`. The esacpe velocity from a planet whose radius is twice that of the earth and mean density is same as that of the earth is `2 upsilon_(e)`.
Statement-2 : `upsilon_(e) = sqrt(g R)`
View SolutionAs observed from the earth, the sun appears to move an approx. circular orbit. For the motion of another planet like mercury as observed from the earth, this would
View SolutionDifferent points in the earth are at slightly different distance from the sun and hence experience different force due to gravitation. For a rigid body, we know that if various forces act at various points in it, the resultant motion is as if a net force acts on the `CM` (centre of mass) causing translation and a net torque at the `CM` causing rotation around an axis through the `CM`. for the earth-sun system (approximating the earth as a uniform density sphere).
View SolutionSatellites orbiting the earth have finite life and sometimes debris of satellites fall to the earth. This is because,
View SolutionBoth earth and moon are subjected to the gravitational force of the sun. as observed from the sun, the orbit of the moon
View SolutionIn our solar system, the inter-planetery region has chunks of matter (much smaller in size compared to planets) called asteriods. They
View SolutionChoose the wrong option.
View Solutionparticles of masses 2M m and M are resectively at points A , B and C with ` AB = (1)/(2) (BC)` m is much - much smaller than M and at time ` t=0` they are all at rest as given in figure . As subsequent times before any collision takes palce .
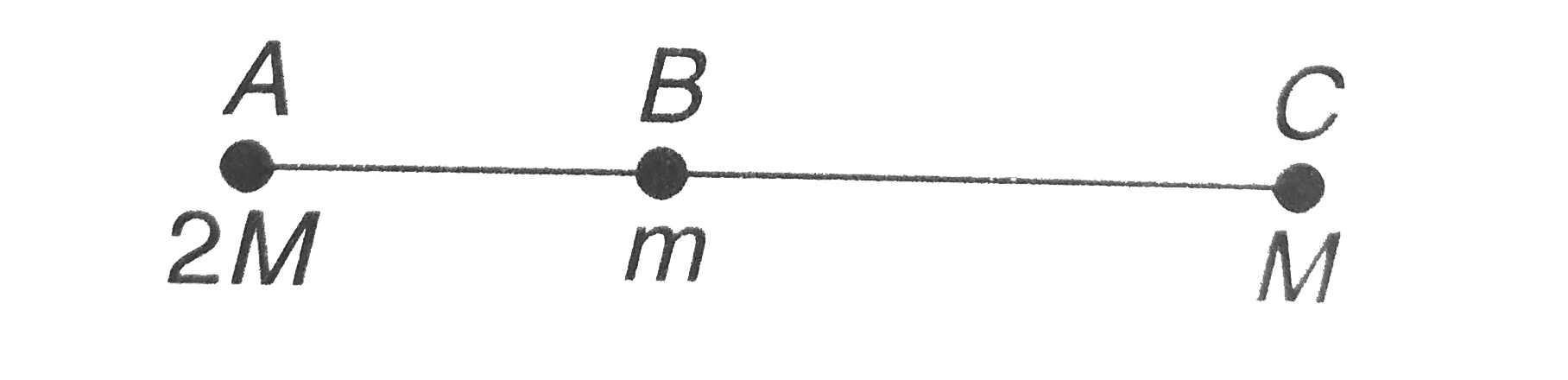
View SolutionIf the law of gravitational, instead of being inverse-square law, becomes an inverse-cube law
View SolutionIf the mass of the sun were ten times smaller and the universal gravitational constant were ten times larger in magnitude, which of the following is not correct?
View SolutionIf the sun and the planets carried huge amounts of opposite charges
View SolutionThere have been suggestions that the value of the gravitational constant `G` becomes smaller when considered over very large time period (in billions of years) in the future. If that happens, for our earth
View SolutionSupposing Newton's law of gravitation for gravitation force `F_(1)` and `F_(2)` between two masses `m_(1)` and `m_(2)` at positions `r_(1)` and `r_(2)` read `F_(2)=-F_(2)=(r_(12))/(r_(12)^(3))GM_(0)^(2)((m_(1)m_(2))/(M_(0)^(2)))^(n)` where `M_(0)` is a constant dimension of mass, `r_(12)=r_(1)-r_(2)` and `n` is number. In such a case.
View SolutionWhich of the following are true?
View SolutionThe centre of mass of a body
View SolutionThe largest and the shortest distance of the earth from the sun are `r_(1)` and `r_(2)`, its distance from the sun when it is at the perpendicular to the major axis of the orbit drawn from the sun
View SolutionA satellite is launched into a circular orbit of radius `R` around the earth. While a second is lunched into an orbit of radius `1.01R` The period of the second satellite is longer than the first one by approximately:
View SolutionA geo-stationary stellite orbits around the earth in a circular orbit of radius 36,000km. Then, the time period of a spy stellite orbitting a few hundred km above the earth's surface `(R_(earth) = 6400km)` will approximately be
View SolutionTwo small satellies move in a circular orbits around the earth, at disatnce `r` and `(r + dr)` from the centre of the earth. Their time periods of rotation ate `T` and `T + dT (Delta r lt lt b r, DeltaT lt lt T)`. Then
View SolutionA system of binary stars of mass `m_(A)` and `m_(B)` are moving in circular orbits of radii `r_(A)` and `r_(B)` respectively. If `T_(A)` and `T_(B)` are at the time periods of masses `m_(A)` and `m_(B)` respectively then
View SolutionA geostationary satellite is orbiting the earth at a height of `5R` above the surface of the earth, `2R` being the radius of the earth. The time period of another satellite in hours at a height of `2R` form the surface of the earth is
View SolutionA satellite moves in a circle around the earth. The radius of this circle is equal to one half of the radius of the moon's orbit. The satellite completes one revolution is :
View SolutionA geostationary satellite orbits around the earth in a circular orbit of radius `3600 km`. Then the time period of satellite orbiting `= 2600 km` above the earth's surface `(R_(earth) = 6400 km)` will appoximetely be
View SolutionIf the distance between the earth and the sun were half its present value, the number of days in a year would have been
View SolutionA U-tube with both ends open to the atmosphere is partially filled with water. Oil, which is immiscible with water. Is poured into one side until it stands at a distance of `10 mm` above the water level on the other side. Meanwhile the water rises by `65mm` from its original level (see diagram). The density of the oil is:

View SolutionA solid sphere of uniform density and radius `R` applies a gravitational force of attraction equal to `F_(1)` on a particle placed at `P`, distance `2R` from the centre `O` of the sphere. A spherical cavity of radius `R//2` is now made in the sphere as shown in figure. The particle with cavity now applies a gravitational force `F_(2)` on same particle placed at `P`. The radio `F_(2)//F_(1)` will be
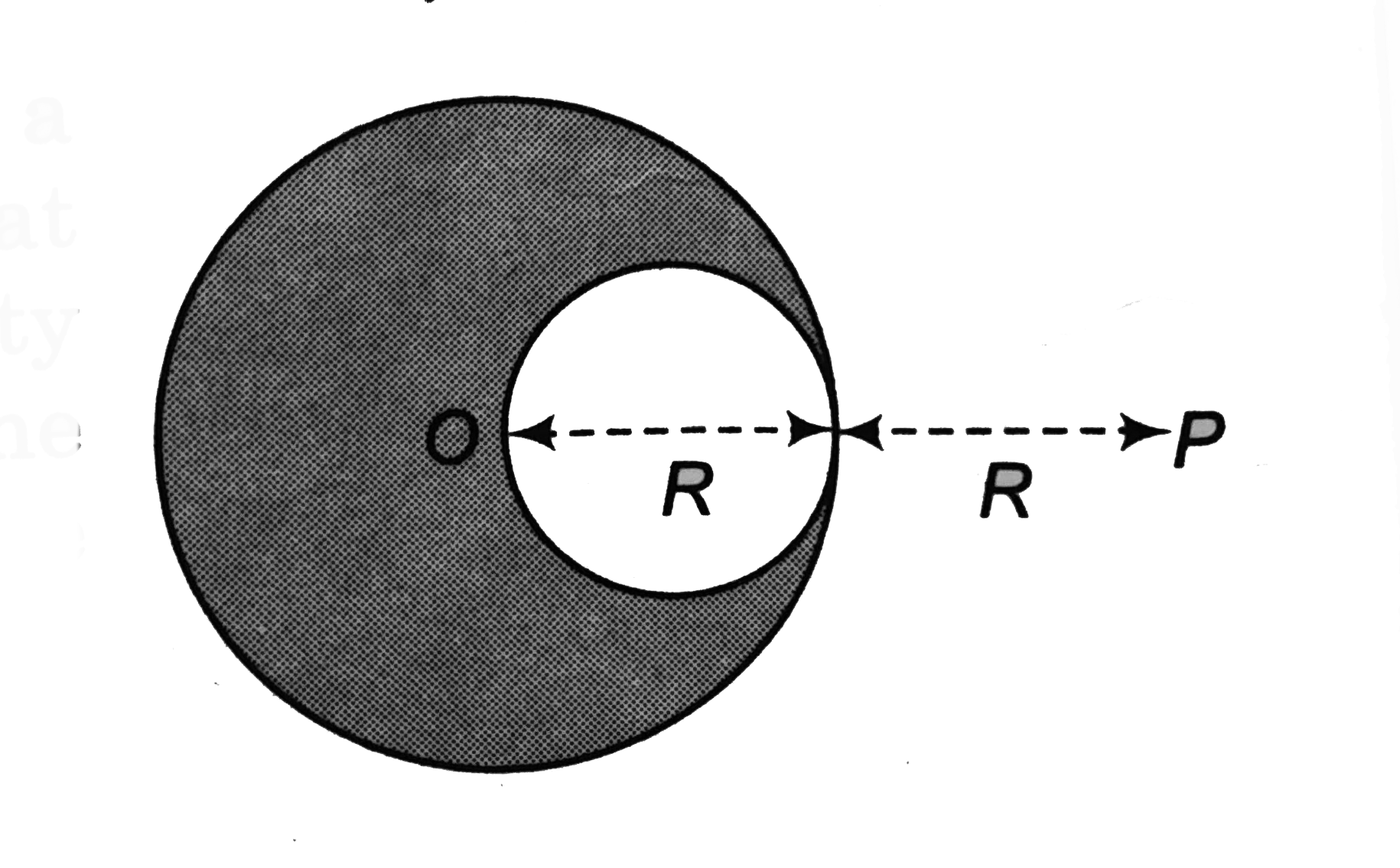
View SolutionA solid sphere of uniform density and radius `R` applies a gravitational force of attraction equal to `F_(1)` on a particle placed at `P`, distance `2R` from the centre `O` of the sphere. A spherical cavity of radius `R//2` is now made in the sphere as shown in figure. The particle with cavity now applies a gravitational force `F_(2)` on same particle placed at `P`. The radio `F_(2)//F_(1)` will be

View SolutionIn the above question, if the soild sphere is a large rock, what is the gravitational acceleration at a point on the surface of the rock at a point just above the cavity ?
View SolutionSuppose the acceleration due to gravity at earth's surface is `10ms^-2` and at the surface of Mars it is `4.0ms^-2`. A passenger goes from the to the mars in a spaceship with a constant velocity. Neglect all other object in sky. Which part of figure best represent the weight (net gravitational force) of the passenger as a function of time?
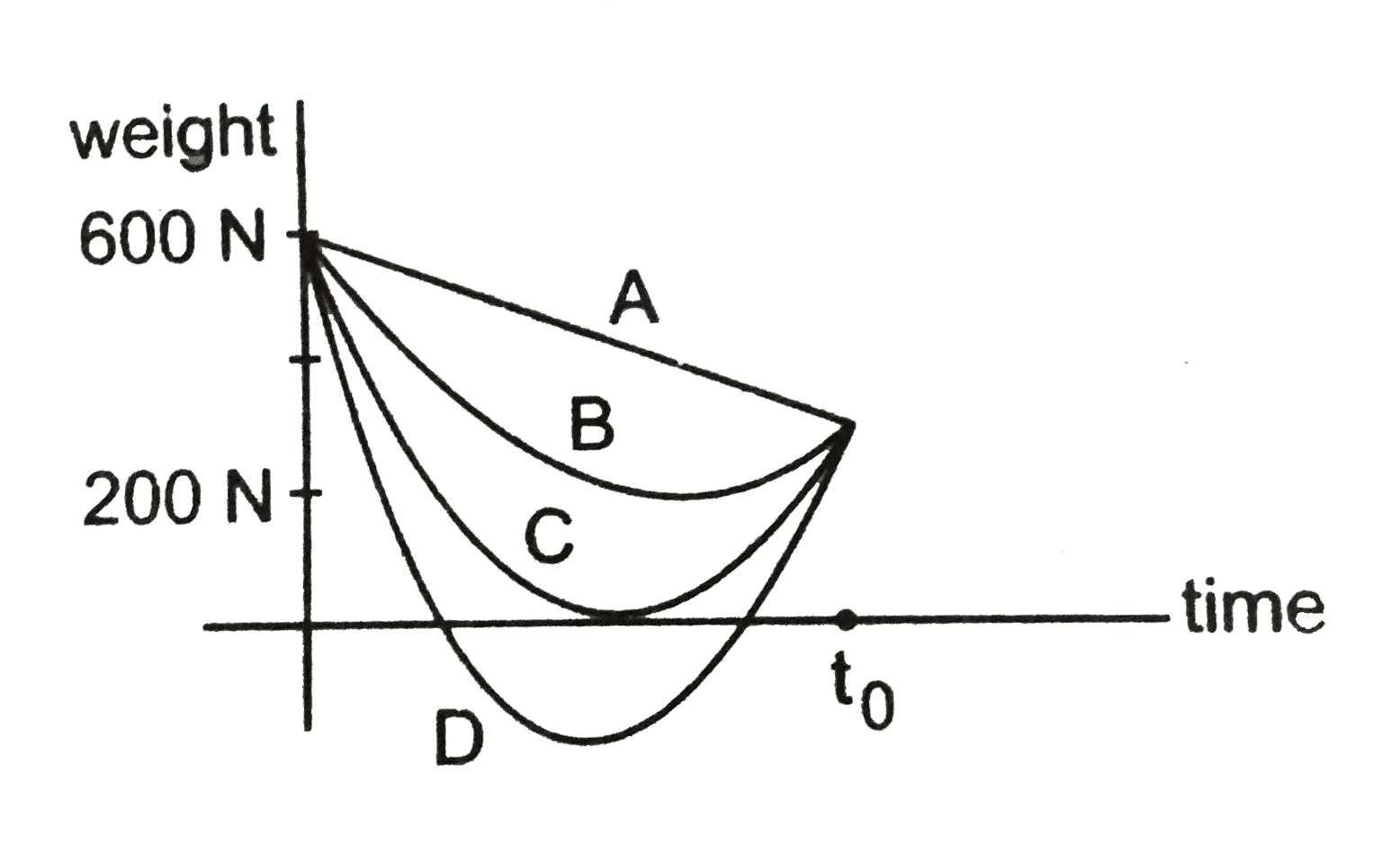
View SolutionA mass m is at a distance a from one end of a uniform rod of length l and mass M. Find the gravitational force on the mass due to the rod.

View SolutionA larger spherical mass M is fixed at one position and two identical point masses m are kept on a line passing through the centre of M. The point masses are connected by rigid massless rod of length l and this assembly is free to move along the line connecting them. All three masses interact only throght their mutual gravitational interaction. When the point mass nearer to M is at a distance r =3l form M, the tensin in the rod is zero for `m =k((M)/(288)).` The value of k is
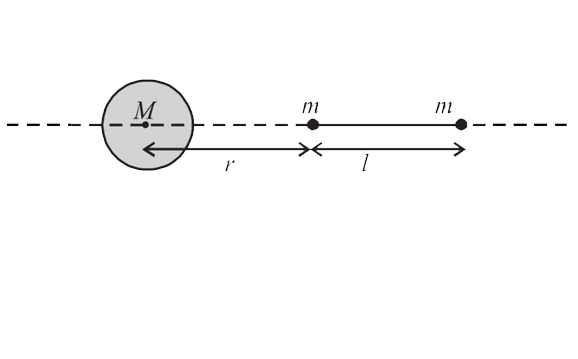
View SolutionFor particles of equal masses M that move along a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
View SolutionTwo spherical bodies of mass M and 5M & radii R & 2R respectively are released in free space with initial separation between their centres equal to 12R. If they attract each other due to gravitational force only, then the distance covered by the smallar body just before collision is
View SolutionA body weighs `700gm` wt on the surface of the earth. How much will it weigh on the surface of a planet whose mass is `1/7` and radius is half that of the earth
View SolutionMass remaining constant, the radius of the earth shrinks by 1%. The acceleration due to gravity on the earth's surface would
View SolutionThe density of a newly discovered planet is twice that of earth. The acceleration due to gravity at the surface of the planet is equal to that at the surface of the earth. If the radius of the earth is `R`, the radius of the planet would be
View SolutionThe dependence of acceleration due to gravity `g` on the distance `r` from the centre of the earth, assumed to br a sphere of radius `R` of uniform density is as shoen in Fig. below:

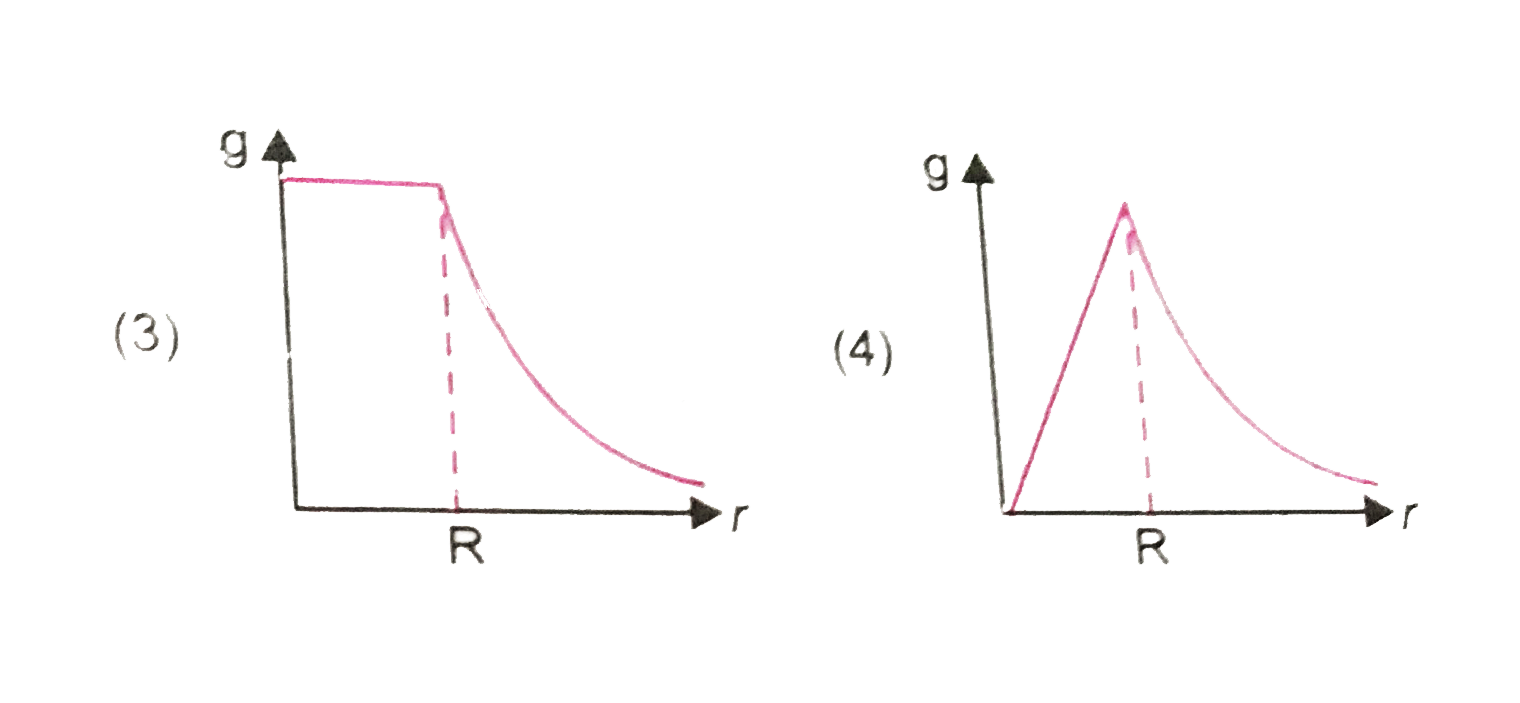
The correct figure is
View SolutionA planet of radius `R=(1)/(10)xx(radius of Earth)` has the same mass density as Earth. Scientists dig a well of depth`(R )/(5)` on it and lower a wire of the same length and a linear mass density `10^(-3) kg m(_1)` into it. If the wire is not touching anywhere, the force applied at the top of the wire by a person holding it inplace is (take the radius of Earth`=6xx10^6m` and the acceleration due to gravity on Earth is `10ms^(-2)`
View SolutionA particle hanging from a spring stretches it by 1 cm at earth's surface. How much will the same particle stretch the spring at a place 800 km above the earth's surface/ Radius of the earth=6400 km.
View SolutionWhat is the percentage change in the value of `g` as we shift from equator to pole on the surface of earth ? (Given equatorial radius of earth is greater than polar radius by `21 km` and mean radius of earth is `6300 km`).
View SolutionA body weights 98 N on a spring balance at the north pole. What will be its weight recorded on the same scale if it is shifted to te equator? Use g=`GM/R^2=9.8m/s^2` and the radius of the earth R=6400 km.
View SolutionThe ratio of radii of earth to another planet is `2//3` and the ratio of their mean densities is `4//5`. If an astronaut can jump to a maximum height of `1.5 m` on the earth, with the same effort, the maximum height he can jump on the planet is
View SolutionA body is weighed with a spring balance in a train at rest, shown a weight `W`. When the train begins to move with a velocity `upsilon` around the equator from west to east and if the angular velocity of the train is `omega` then the weight shown by spring balance is
View SolutionA spherically symmetric gravitational system of particles has a mass density` rho={(rho_0,for, r,lt,R),(0,for,r,gt,R):}` where`rho_0` is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed v as a function of distahce `r(0ltrltOO)` form the centre of the system is represented by
View SolutionThe gravitational field due to a mass distribution is given by `E=K/x^3` in X-direction. Taking the gravitational potential to be zero at infinity, find its value at a distance x.
View SolutionTwo concentric spherical shells `A` and `B` of radii `R` and `2R` and mases `4M`, and `M`, respectively are placed in space as shown in Fig. The gravitational potential at `P` at a distance `r(R lt r lt 2R)`from the centre of shells is

View SolutionAt what height from the surface of earth the gravitation potential and the value of `g` are `- 5.4 xx 10^(7) J kg^(-2)` and `6.0 ms^(-2)` respectively ? Take the radius of earth as `6400 km`:
View SolutionFrom a solid sphere of mass M and radius R, a spherical portion of radius R/2 is removed, as shown in the figure Taking gravitational potential `V =0at r = oo,` the potential at (G = gravitational constant)

View SolutionA uniform rod of mass `m` and length `l` is taken. Find the gravitational field intensity at point `P` at distance `d` which is on the perpendicular bisector of the rod as shown in Fig.
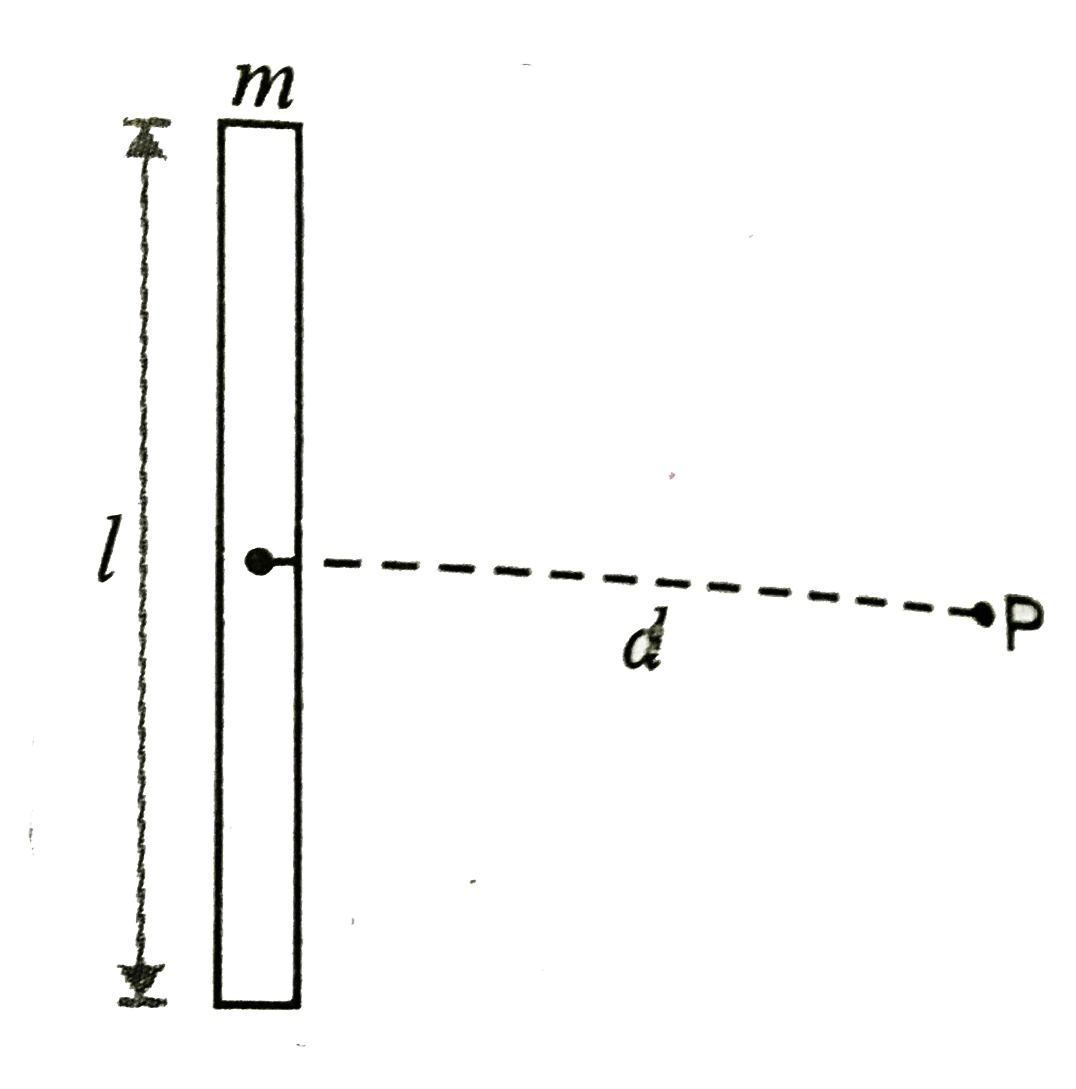
View SolutionA point `P` lies on the axis of a fixed ring of mass `M` and radius `a`, at a distance `a` from its centre `C`. A small particle starts from `P` and reaches `C` under gravitational attraction only. Its speed at `C` will be.
View SolutionInfinite number of masses, each of `1 kg`, are placed along the x-axis at `x = +- 1m, +- 2m, +-4m, +- 8m, +- 16m`.. The gravitational of the resultant gravitational potential in term of gravitaitonal constant `G` at the origin `(x = 0)` is
View SolutionDependence of intensity of gravitational field `(E)` of earth with distance `(r)` from centre of earth is correctly represented by
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance `a/2` from the centre.
View SolutionA person brings a mass of 1 kg from infinity to a point . Initally the mass was at rest but it moves at a speed of 2 `ms^-1` as it reaches A. The work done by the person on the mass is -3J. The potential at A is
View SolutionThe change in the gravitational potential energy when a body of a mass `m` is raised to a height `nR` above the surface of the earth is (here `R` is the radius of the earth)
View SolutionFour particles each of mass m are placed at the vertices of a square of side l. the potential at the centre of square is
View SolutionA satellite of mass `m` is in a circular orbit of radius `2R_(E)` about the earth. The energy required to transfer it to a circular orbit of radius `4R_(E)` is (where `M_(E)` and `R_(E)` is the mass and radius of the earth respectively)
View SolutionA body is projected vartically upwards from the bottom of a crater of moon of depth `( R)/(100)` where R is the radius of moon with a velocity equal to the escape velocity on the surface of moon. Calculate maximum height attained by the body formt eh surface of the moon.
View SolutionA body is released from a point of distance `R'` from the centre of earth. Its velocity at the time of striking the earth will be `(R’gtR_(e))`
View SolutionA rocket is launched vertically from the surface of earth with an initial velocity `v`. How far above the surface of earth it will go? Neglect the air resistance.
View SolutionIf a body is to be projected vertically upwards from earth's surface to reach a height of `10R` where `R` is the radius of earth. The velocity required to be si is
View SolutionA body is projected vertically upwards from the surface of a planet of radius `R` with a velocity equal to hall the escape velocity for that planet. The maximum height attained by the body is
View SolutionThe earth is assumed to be a sphere of raduis `R`. A plateform is arranged at a height `R` from the surface of the `fv_(e)`, where `v_(e)` is its escape velocity form the surface of the earth. The value of `f` is
View SolutionWhat is the minimum energy required to launch a satellite of mass m from the surface of a planet of mass M and radius R in a circular orbit at an altitude of 2R?
View SolutionA body of mass `m` is lifted up from the surface of earth to a height three times the radius of the earth `R`. The change in potential energy of the body is
View SolutionA thin uniform disc (see figure) of mass M has outer radius 4R and inner radius 3R. The work required to take a unit mass for point P on its axis to infinity is

View SolutionWhich one of the following plots represents the variation of the gravitational field on a particle with distance `r` due to a thin spherical shell of raduis `R`? (`r` is measured from the centre of the spherical shell).
View SolutionKepler's third law states that square of period revolution `(T)` of a planet around the sun is proportional to third power of average distance `i` between sun and planet i.e. `T^(2)=Kr^(3)`
here `K` is constant
if the mass of sun and planet are `M` and `m` respectively then as per Newton's law of gravitational the force of alteaction between them is `F=(GMm)/(r^(2))`, here `G` is gravitational constant. The relation between `G` and `K` is described as
View SolutionSuppose the gravitational force varies inversely as the nth power of distance. Then the time period of a planet in circular orbit of radius 'R' around the sun will be proportional to
View SolutionWhich of the following statement is correct about satellites?
View SolutionA rocket is launched normal to the surface of the earth, away from the sun, along the line joining the sun and the earth. The sun is `3 xx 10^(5)` times heavier than the earth and is at a distance `2.5 xx 10^(4)` times larger than the radius of the earth. the escape velocity from earth's gravitational field is `u_(e) = 11.2 ms^(-1)`. The minmum initial velocity `(u_(e)) = 11.2 ms^(-1)`. the minimum initial velocity `(u_(s))` required for the rocket to be able to leave the sun-earth system is closest to (Ignore the rotation of the earth and the presence of any other planet
View SolutionA satellite orbits around the earth in a circular orbit with a speed `upsilon` and orbital radius `r`. If it loses some energy, then `upsilon` and `r` chsnges as
View SolutionA satellite in a force-free space sweeps stationary interplantary dust at a rate `(dM)/(dt) = beta upsilon`, where `upsilon` is the speed of escaping dust w.r.t. satellite and `M` is the mass of saetllite at that instant. The acceleration of satellite is
View SolutionA satellite is moving around the earth's with speed `v` in a circular orbit of radius `r`. If the orbit radius is decreases by `1%` , its speed will
View SolutionIf a satellites is revolving close to a planet of density `rho` with period `T`, show that the quantity `rho T^(2)` is a universal constant.
View SolutionThe radii of circular orbits of two satellite `A` and `B` of the earth are `4R` and `R`, respectively. If the speed of satellite `A` is `3v`, then the speed of satellite `B` will be
View SolutionEscape velocity of a body `1 kg` mass on a planet is `100 ms^(-1)`. Gravitational potential energy of the body at that planet is
View SolutionTwo bodies, each of mass M, are kept fixed with a separation 2L. A particle of mass m is projected from the midpoint of the line joining their cehntres, perpendicualr to the line. The gravitational constant is G. The correct statement (s) is (are)
View SolutionA satellite is moving with a constant speed 'V' in a circular orbit about the earth. An object of mass 'm' is ejected from the satellite such that it just escapes form the gravitational pull of the earth. At the tme of its ejection, the kinetic energy of the object is
View SolutionThe ratio of escape velocity at earth `(v_(e))` to the escape velocity at a planet `(v_(y))` whose radius and density are twice
View SolutionA satellite S is moving in an elliptical orbit around the earth. The mass of the satellite is very small compared to the mass of the earth.
View SolutionA satellite is revolving in a circular orbit at a height 'h' from the earth's surface (radius of earth R, h ltltR). The minimum increase in its orbital velocity required, So that the satellite could escape from the erth's gravitational field, is close to :(Neglect the effect of atomsphere.)
View SolutionA particle is fired vertically from the surface of the earth with a velocity `kupsilon_(e)`, where `upsilon_(e)` is the escape velocity and `klt1`. Neglecting air resistance and assuming earth's radius as `R_(e)`. Calculated the height to which it will rise from the surface of the earth.
View SolutionA black hole is an object whose gravitational field is so strong that even light cannot escape from it. To what approximate radius would earth (mass `=5.98xx10^(24)kg`) have to be compresed to be a black hole?
View SolutionA bullet is fired vertically upwards with a velocity `upsilon` from the surface of a spherical planet when it reaches its maximum height, its acceleration due to the planet's gravity is `(1)/(4)th` of its value at the surface of the planet. If the escape velocity from the planet is `V_("escape") = upsilon sqrt(N)`, then the value of `N` is : (ignore energy loss due to atmosphere).
View SolutionWhich of the following is true for a satellite in an orbit
View SolutionWhich of the following statements are true about acceleration due to gravity
View SolutionWhich of the following statements are correct about a planet rotating around the sun in an elleptical orbit
View SolutionIf two satellites of different masses are revolving in the same orbit, they have the same
View SolutionChoose the correct statement`//(s)`
View SolutionThe escape velocity of an object projected from the surface of a given planet is independent of
View Solution
MULTIPLE CHOICE QUESTIONS questions and complete solutions for chapter GRAVIATION of PRADEEP PHYSICS (HINGLISH) of Class 11
All Exercises from PRADEEP Class 11 PHYSICS GRAVIATION
- ADDITIONAL EXERCISES
- ADVANCED PROBLEMS FOR COMPETITIONS
- Assertion-Reason Type Questions
- CONCEPTUAL PROBLEMS
- CONCEPTUAL PROBLEMS I.
- CONCEPTUAL PROBLEMS II.
- CONCEPTUAL PROBLEMS III.
- CONCEPTUAL PROBLEMS IV.
- CONCEPTUAL PROBLEMS V.
- CURIOSITY QUESTION
- FILL IN THE BLANKS
- FOCUS Multiple Choice questions I.
- Integer Type Questions
- LONG ANSWER QUESTIONS
- MULTIPLE CHOICE QUESTIONS
- MULTIPLE CHOICE QUESTIONS -II
- Multiple Choice questions II.
- Multiple Choice questions III.
- Multiple Choice questions IV.
- Multiple Choice questions V.
- NCERT
- NCRET MULTIPLE CHOICE QUESTIONS -I
- PROBLEMS FOR PRACTIVE
- PROBLEMS FOR PRACTIVE A
- PROBLEMS FOR PRACTIVE B
- PROBLEMS FOR PRACTIVE C
- PROBLEMS FOR PRACTIVE D
- PROBLEMS FOR PRACTIVE E
- PROBLEMS FOR PRACTIVE F
- PROBLEMS FOR PRACTIVE G
- PROBLEMS FOR PRACTIVE H
- PROBLEMS FOR PRACTIVE I
- PROBLEMS FOR PRACTIVE J
- PROBLEMS FOR PRACTIVE K
- QUESTIONS
- Sample Problem
- SHORT ANSWER QUESTIONS
- SHORT ANSWER QUESTIONS I.
- SHORT ANSWER QUESTIONS II.
- SHORT ANSWER QUESTIONS III.
- SHORT ANSWER QUESTIONS IV.
- SHORT ANSWER QUESTIONS V.
- SOLVED EXAMPLES
- SOLVED EXAMPLES TYPE A
- SOLVED EXAMPLES TYPE B
- SOLVED EXAMPLES TYPE C
- SOLVED EXAMPLES TYPE D
- SOLVED EXAMPLES TYPE E
- SOLVED EXAMPLES TYPE F
- SOLVED EXAMPLES TYPE G
- SOLVED EXAMPLES TYPE H
- SOLVED EXAMPLES TYPE I
- SOLVED EXAMPLES TYPE J
- SOLVED EXAMPLES TYPE K
- VALUE BASED QUESTIONS
- VERY SHORT ANS. QUESTIONS
- VERY SHORT ANS. QUESTIONS I.
- VERY SHORT ANS. QUESTIONS II.
- VERY SHORT ANS. QUESTIONS III.
- VERY SHORT ANS. QUESTIONS IV.
- VERY SHORT ANS. QUESTIONS V.
- VERY SHORT ANSWER QUESTIONS