Complete Solutions to Long Answer questions of chapter PROPERTIES OF BULK MATTER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | PROPERTIES OF BULK MATTER |
| PRADEEP | Long Answer questions |
| Number Of Questions | 33 |
| Academic Year | 2023-24 |
Explain modulus of elasticity and its various forms.
View SolutionDiscuss atleast three important applications of elasticity.
View SolutionExplain the working of (i) hydraulic lift (ii) hydraulic breaks.
View SolutionShow that atmosphere exerts pressure and describe Torricelli's experiment to study the atmospheric pressure.
View SolutionDefine the terms molecular range, sphere of influence and surface film.
View SolutionExplain surface tension. Discuss molecular theory of surface tension.
View SolutionDerive an expression for the excess pressure (i) inside a liquid drop (ii) inside a soap bubble.
View SolutionDefine Capillarity and angle of contact. Derive an expression for the ascent of a liquid in a capillary tube.
View SolutionExpalin streamline flow, laminar flow and turbulent flow.
View SolutionWhat are different forms of energy possessed by a flowing liquid? Write expression of them.
View SolutionState and prove Bernoulli's theorem.
View SolutionDefine three coefficeints of thermal expansion. Establish relation between them.
View SolutionExplain what is meant by specific heat of a substance. What are its units? How is molar specific heat different from specific heat?
View SolutionDefine two principal specific heats of a gas. Which is greater and why?
View SolutionWhat do you mean by change of state of a substance?
View SolutionExplain the three modes of transfer of heat with illustrations.
View Solutionwhat is meant by thermal conductivity and its coefficient . What are its SI units and cgs units.
View SolutionState and explain Newton's law of cooling. Also discuss its experimental verification.
View SolutionConsider a long steel bar under a tensile stress due to forces F, acting at the edges along the length of the bar

Consider a plane making an angle `theta` with the length. What are the tensile and shering stresses on this plane ? (a) For what angle is the tensile stress a maximum ? (b) For what angle is the shearing stress a maximum ?
View SolutionA steel wire of mass `mu` per unit length with a circular cross-section has a radius of `0.1cm`. The wire is of length `10m` when measured lying horizontal, and hangs from a hook on the wall. A mass fo `25kg` is hung from the free end of the wire. Assume the wire to be uniform and laterla strain `lt lt` logitudinal strain. If density of steel is `7860 kg m^(-3)` and Young's modulus is `2xx10^(11) N//m^(2)` then the extension in the length fo the wire is
View SolutionA steel rod of length 2l cross-sectional area A and mass M is set rotating in a horizontal plane about an axis passing through its centre and perpendicular to its length with constant angular velocity `omega`. If Y is the Young's modulus for steel, find the extension in the length of the rod. (Assume the rod is uniform.)
View SolutionAn equilateral triangle ABC if formed by two Cu rods AB and BC and one Al rod

it is heated in such a way that temperature of each rod increases by `Delta T.` Find change in the angle ABC. [Coeff. Of linear expansion for Cu. is `alpha_1,` Coeff. of linear expansion for Al is `alpha_2]`
View SolutionIn nature, the failure of structural members usually result from large torque because of twisting or bending rather than due to tensile or compressive strains. This process of structural breakdown is called buckling and in cases of tall cylindrical structures like trees, the torque is caused by its own weight bending the structure. Thus, the vertical through the centre of gravity does not fall within the base. The elastic torque caused because of this bending about the central axis of the tree is given by `(Ypir^(4))/(4R)`. Y is the Young's modulus, r is the radius of the trunk and R is the radius of curvature of the bent surface along the height of the tree containing the centre of gravity (the neutral surface). Estimate the critical height of a tree for a given radius of the trunk.
View SolutionA stone of mass m is tied to an elastic string of negligble mass and spring constant k. The unstretched length of the string is L and has negligible mass. The other end of the string is fixed to a nail at a point p. Initially the stone is at the same level as the point P. The stone is dropped vertically from point P.
(a) Find the distance y from the top when the mass comes to rest for an instant, for the first time.
(b) What is the maximum velocity attained by the stone in this drop?
(c) What shall be the nature of the motion after the stone has reached its lowest point?
View Solution(a) Pressure decreases as one ascends the atmosphere. If the density of air is `rho,` What is the change in pressure dp over a differential height dh ? (b) Considering the pressure p to be proportional to the density, find the pressure p at a height h if the pressure on the sureface of the earth is `p_0.` (c ) If `p_0 = 1.03 xx 10^5 Nm^(-2), rho_0 = 1.29kg m^(-3) and g = 9.8 ms^(-2), ` at what height will the pressure drop to `(1//10)` the value at the surface of the earth ? (d) This model of the atmosphere works for relatively small distance. Identify the underlying assumption that limits the model.
View SolutionSurface tension is exhibited by liquids due to force of attraction between molecules of the liquid. The surface tension decreases with increase in temperature and vanishes at boiling point. Given that the latent heat o vaporisation for water `L_(v)=540 "k cal kg"^(-1)`, the mechanical equivalent of heat `J. 4.2 "J cal"^(-1)` , density of water `rho_(w)=10^(3) kg l^(-1)` , Avagardro's number `N_(A)=6.0xx 10^(26)K "mole"^(-6)` and the molecular weight of water `M_(A)=10` kg for 1 k mole.
(a) Estimate the energy required for one molecules of water to evaporate.
(b) Show that the inter-molecular distance for water is `d=[(M_(A))/(N_(A))xx(1)/(rho_(w))]^(1//3)` and find its values.
(c) 1 g of water in the vapour state at 1 atm occupies `1601 cm^(3)` . Estimate the inter-molecules distance at boiling point, in the vapour state.
(d) During vaporisation a molecules overcomes a force F, assumed constant, to go from an inter-molecules distance d to d'. Estimate the value of F.
(e) Calculate F/d , which is a measure of the surface tension.
View SolutionA hot air balloon is a sphere of radius 8 m . The air inside is at a temperature of `60^@C.` How large a mass can the balloon lift when the outside temperature is `20^@C ?` (Assume air is an ideal gas `R = 8.314 J mol e ^(-1) K^(-1), 1 atm. = 1.013 xx 10^5 Pa` , the membrane tension is `5 Nm^(-1))`
View SolutionWe would like to perpare a scale whose length does not change with temperature. It is proposed to prepare a unit scale f this type whose length remains, say 10 cm. We can use a bimetallic strip made of brass and iron each of different length (both components) would change in such a way that differnece between theri lenght rermain constant. If `alpha_(iron) = 1.2 xx 10^(-5)//K and alpha_(brass) = 1.8 xx 10^(-5)//K,` what should we take as lenght of each strip ?
View SolutionWe would like to make a vessel whose volume does not change with temperature (take a hing from the problem aobve). We can use brass and iron `(beta_(brass) = 6 xx10^(-5) // K and beta_(iron) = 3.55 xx 10^(-5)//K)` ot create a volume of 100 c c. How do you think you can achieve this.
View SolutionCalculate the stress developed inside a tooth cavity filled with copper when hot tea at temperature of `57^(@)C` is drunk. You can take body (tooth) temperature to be `37^(@)C` and `alpha_(Cu) = 1.7 xx 10^(-5)//^(@)C` bulk modulus for copper `B_(Cu) = 140 xx 10^(9) N//m^(2)`.
View SolutionA rail track made of steel having length 10 m is clamped on a railway line at its two ends
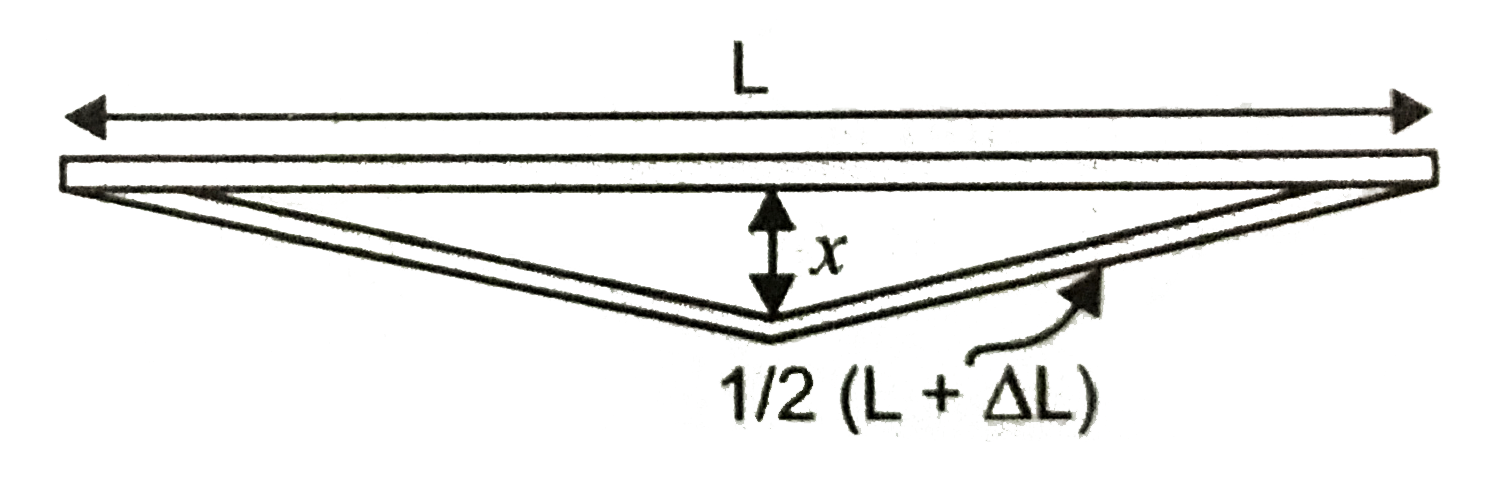
on a summer day due to rise in temperature by `20^@C,` it is deformed as shown in fig. Find x (displacement of the centre) if `alpha_(steel) = 1.2 xx 10^(-5)//^@C.`
View SolutionA thin rod, length `L_(0)` at `0^(@)C` and coefficient of linear expansion `alpha` has its two ends mintained at temperatures `theta_(1)` and `theta_(2)` respectively Find its new length .
View SolutionAc cording to Stefan' law of radiation, a black body radiates energy `sigma T^4` from its unit surface area every second where T is the surface temperature of the black body and `sigma = 5.67 xx 10^(-8) W//m^2 K^4` is known as Stefan's constant. A nuclear weapon may be thought of as a ball of radius 0.5 m When detoneted, it reachs temperature of `10^6 K` and can be treated as a black body. (a) Estimate the power it radiates. (b) if surrounding has water at `30^@C` how much water can 10% of the energy produced evaporate in 1s ? ` [s_w = 4186.0 J//Kg K and L_(upsilon) = 22.6 xx 10^5 J//kg]` (c ) If all this energy U is in the form of radiation, corresponding momentum is ` p = U//c.` How much momentum per unit time does it impart on unit area at a distance of 1 km ?
View Solution
Long Answer questions questions and complete solutions for chapter PROPERTIES OF BULK MATTER of PRADEEP PHYSICS (HINGLISH) of Class 11
All Exercises from PRADEEP Class 11 PHYSICS PROPERTIES OF BULK MATTER
- Advanced problems for competitions
- Asseration - Reason Type Question
- Conceptual Problems
- Curiosity Questions
- Fill in the Blanks A
- Fill in the Blanks B
- Fill in the Blanks C
- Fill in the Blanks D
- Fill in the Blanks E
- Higher Order thinking skells
- Integer Type Questions
- Long Answer questions
- Multiple choice questions
- Multiple choice questions-I
- Multiple choice questions-II
- NCERT Questions
- Problmes for Practice
- Sample problem
- Short Answer Questions
- Solved Examples
- Test Your Grip A
- Test Your grip B
- Test Your Grip C
- Test Your Grip D
- Test Your Grip E
- Value Based Question
- Very short answer questions