Complete Solutions to NCERT Questions of chapter PROPERTIES OF BULK MATTER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | PROPERTIES OF BULK MATTER |
| PRADEEP | NCERT Questions |
| Number Of Questions | 73 |
| Academic Year | 2023-24 |
A steel wire of length `4.7 m` and cross-sectional area `3 xx 10^(-6) m^(2)` stretches by the same amount as a copper wire of length `3.5 m` and cross-sectional area of `4 xx 10^(-6) m^(2)` under a given load. The ratio of Young's modulus of steel to that of copper is
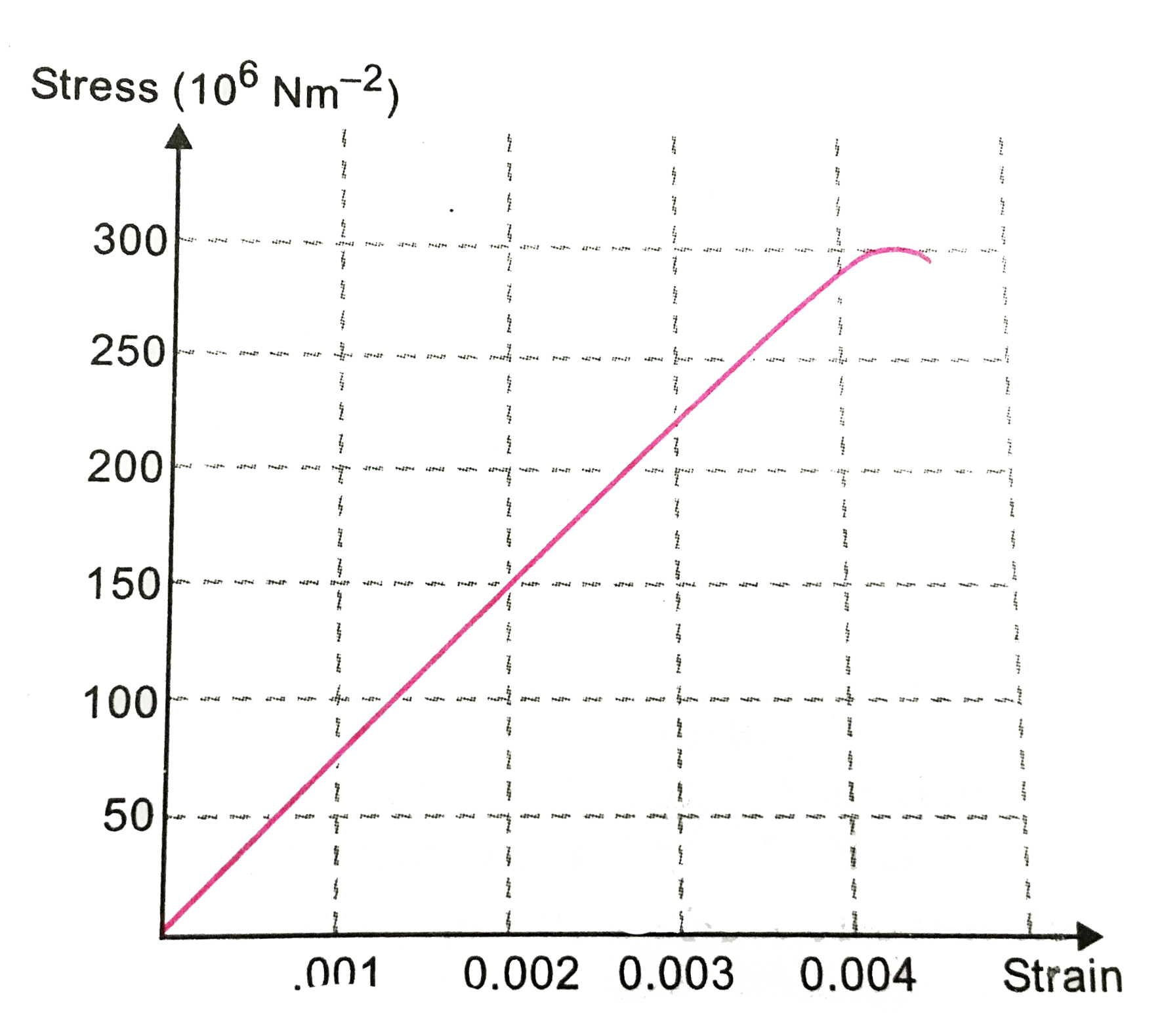
View SolutionFig., shows the stress-strain curve for a given materal. What are (a) Young's modulus and (b) approximate yield strength for this material?
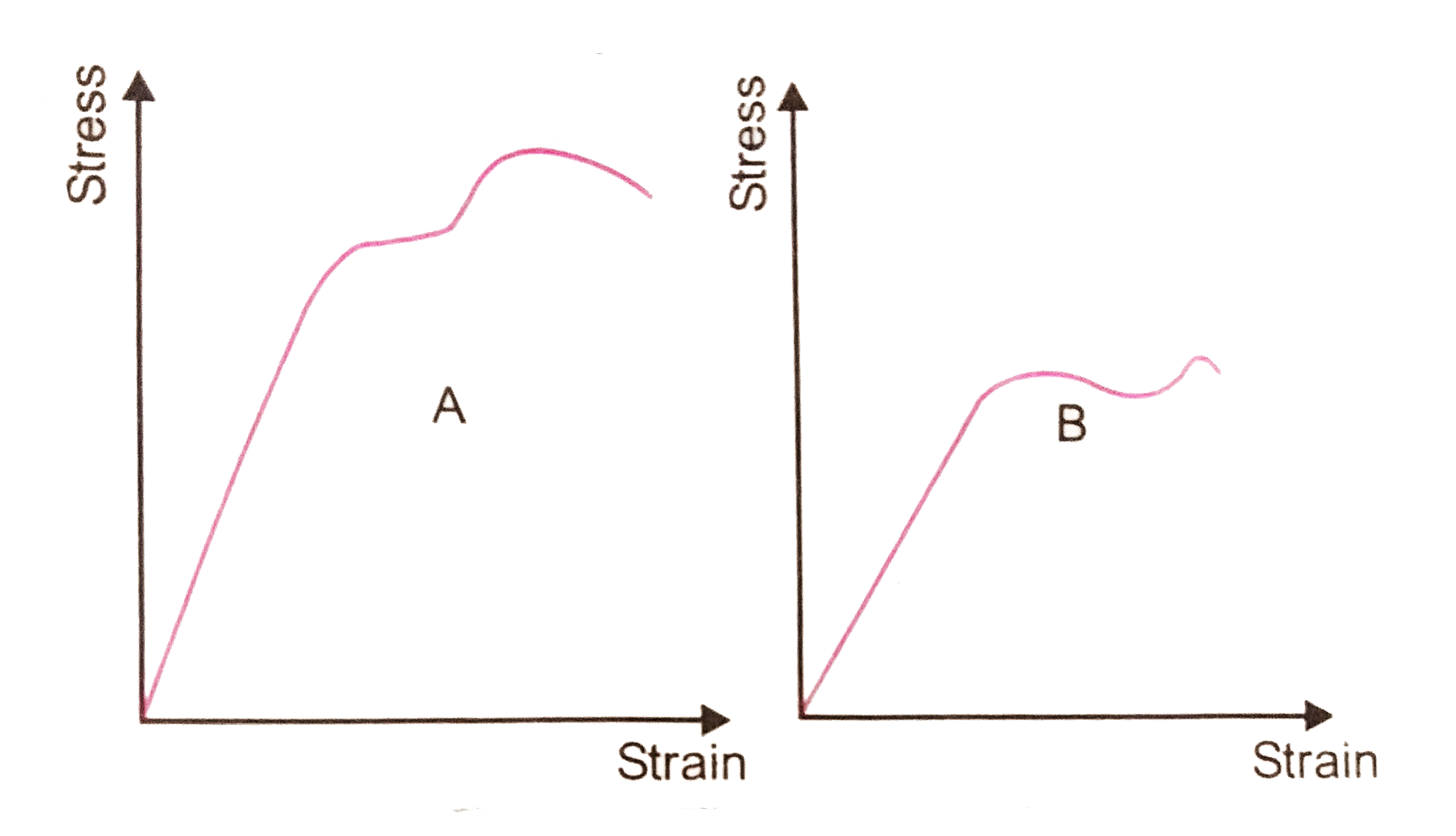
View SolutionThe stress versus strain graph for two materials A and B are shown in fig. the graph are on the same scale. ltbr. (a) Which materail has greater Young's modulus?
(b) which of the two is stronger materail?
View SolutionRead each of the statement below carefully and state, with reasons, if it is true or false.
(a) The modulus of elasticity of rubber is greater than that of steel.
(b) the stretching of a coil is determined by its shear modulus.
View SolutionTwo wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in figure. The unloaded length of steel wire is 1.5 m and that of brass wire is 1.0 m. Compute the elongations of the steel and the brass wires .Young's modulus of steel is `2.0 xx 10^(11)`Pa and that of brass is `9.1 xx 10^(11)` Pa.
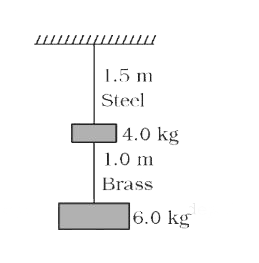
View SolutionThe edges of an aluminum cube are `10 cm` long. One face of the cube is firmly fixed to a vertical wall. A mass of `100 kg` is then attached to the opposite face of the cube. Shear modulus of aluminum is `25 xx 10^(9) Pa`, the vertical deflection in the face to which mass is attached is
View SolutionFour identical hollow cylindrical cloumns of steel support a big structure of mass 50.000 kg. the inner and outer radii of each column are 30 cm and 60 cm respectively. Assume the load distribution to be uniform , calculate the compressional strain of each column. the Young's modulus of steel is `2.0 xx 10^(11) Pa`.
View SolutionA piece of copper having a rectangular cross section of `15.2 xx 19.1 mm` is pulled in tension with 45,500N, force producing only elastic deformation. Calculate the resulting strain. Shear modulus of elasticity of copper is `42 xx 10^(9)Nm^(-2)`.
View SolutionA steel cable with a radius of 1.5 cm support a chairlift at a ski area.if the maximum stress is not to exceed `10^(8) Nm^(-2)`, what is the maximum load the cable can support?
View SolutionA rigid bar of mass 15 kg is supported symmetrically by three wires each 2 m long. Those at each end aer of copper and middle one is of iron. Determine the ratio of their diameters if each is to have the same tensoin. Young's modulus of elasticity for copper and steel are `110 xx 10^(9)Nm^(-2)` and `190 xx 10^(9)Nm^(-2)` respectively.
View SolutionA 14.5 kg mass, fastened to the end of a steel wire of unstretched length 1m, is whirled in a vertical circle with an angular velocity of `2 rev.//s` at the bottom of the circle. The cross-sectional area of the wire is `0.065 cm^(2)` . Calculate the elongation of the wire when the mass is at the lowest point of its path `Y_(steel) = 2 xx 10^(11) Nm^(-2)`.
View SolutionCompute the bulk modulus of water from the following data : initial volume = 100.0 litre, pressure increase = 100.0 atmosphere. Final volume - 100.5 litre . (1 atmosphere = `1.013 xx 10^(5) Pa)`. Compare the ulk modulus of water that of air (at constant temperature). explain in simple terms why the ratio is so large.
View SolutionWhat is the density of ocean water at a depth, where the pressure is 80.0 atm, given that its density at the surface is `1.03 xx 10^(3) kg m^(-3)`? Compressibilty of water `= 45.8 xx 10^(-11) Pa^(-1)`. Given 1 atm. =`1.013 xx 10^(5) Pa`.
View SolutionCompute the fractional change in volume of a glass slab, when subjicted to a hydrautic pressure of 10 atmosphere. Bulk modulus of elasticity of glass = `37 xx 10^(9) Nm^(-2)` and 1 atm = `1.013 xx 10^(5)Pa`.
View SolutionThe volume change of a solid copper cube 20 cm on an edge, when subjected to a pressure of 14 MPa is
(Bulk modulus of copper 140 GPa)
View SolutionHow much should the pressure on a litre of water be changed to compress it by 0.10%? Bull modulus of elasticity of water = `2.2 xx 10^(9) Nm^(-2)`.
View SolutionAnvils made of single crystal of diamond , with shape as shown in fig. are used to investigate behaviour of materials under very high pressure. Flat faces at the narrow end of the anvil have a diameter of 0.5 mm, and the wide ends are subjected to a compressional force of 50,000 N. What is the pressure at the tip of the anvil?

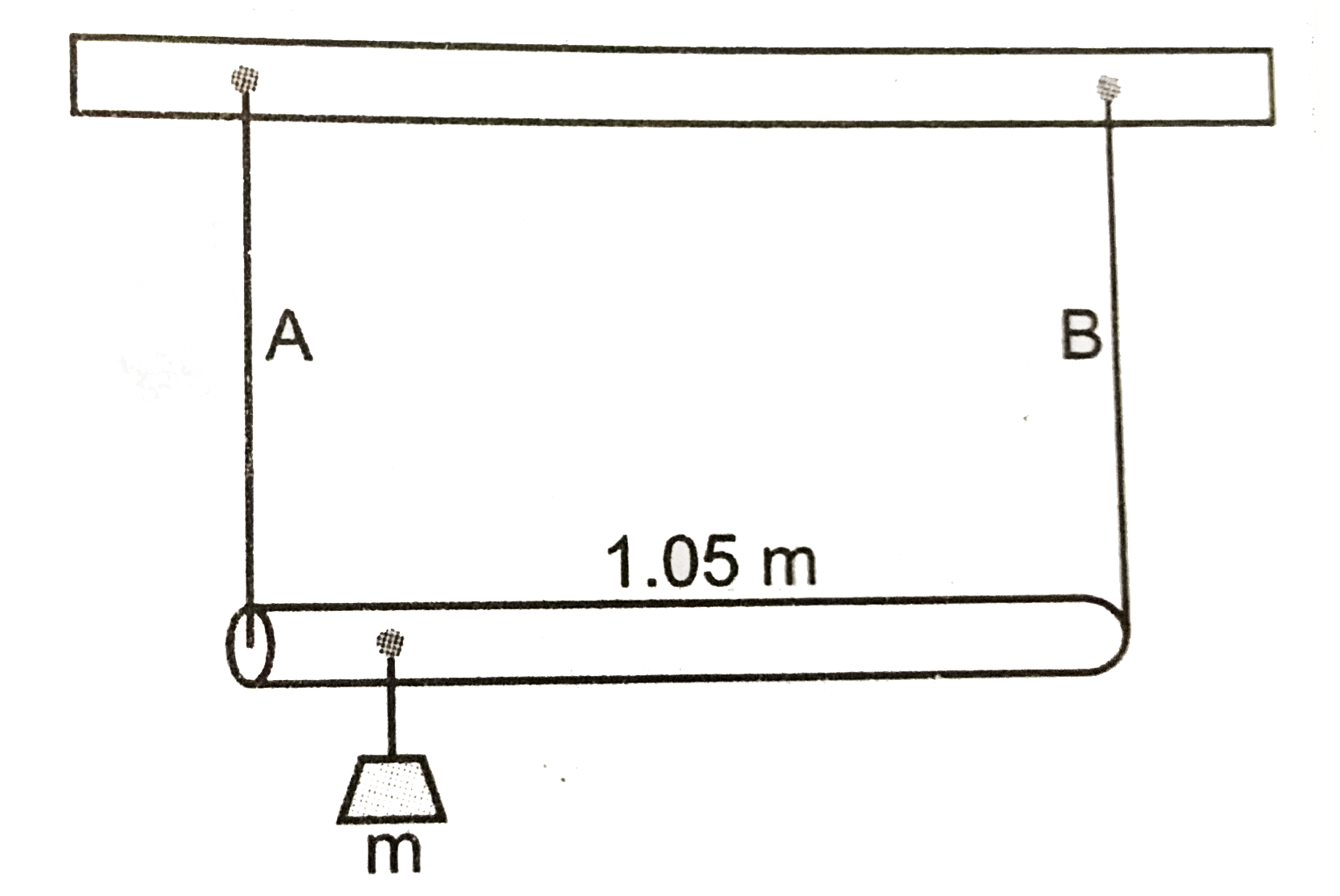
View SolutionA rod of length 1.05 m having negliaible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in fig. The cross-sectional area of wire A and B are `1 mm^(2)` and 2` mm^(2)`, respectively . At what point along the rod should a mass m be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires. Given,
`Y_(steel) = 2 xx 10^(11) Nm^(-2) and Y-(alumi n i um) = 7.0 xx 10^(10)N^(-2)`
View SolutionA mild steel wire of length 1.0 m and cross-sectional are `0.5 xx 10^(-20)cm^(2)` is streached, well within its elastic limit, horizontally between two pillars. A mass of 100 g is suspended from the mid point of the wire, calculate the depression at the mid point.
`g = 10ms^(-2), Y=2 xx 10^(11)Nm^(-2`.
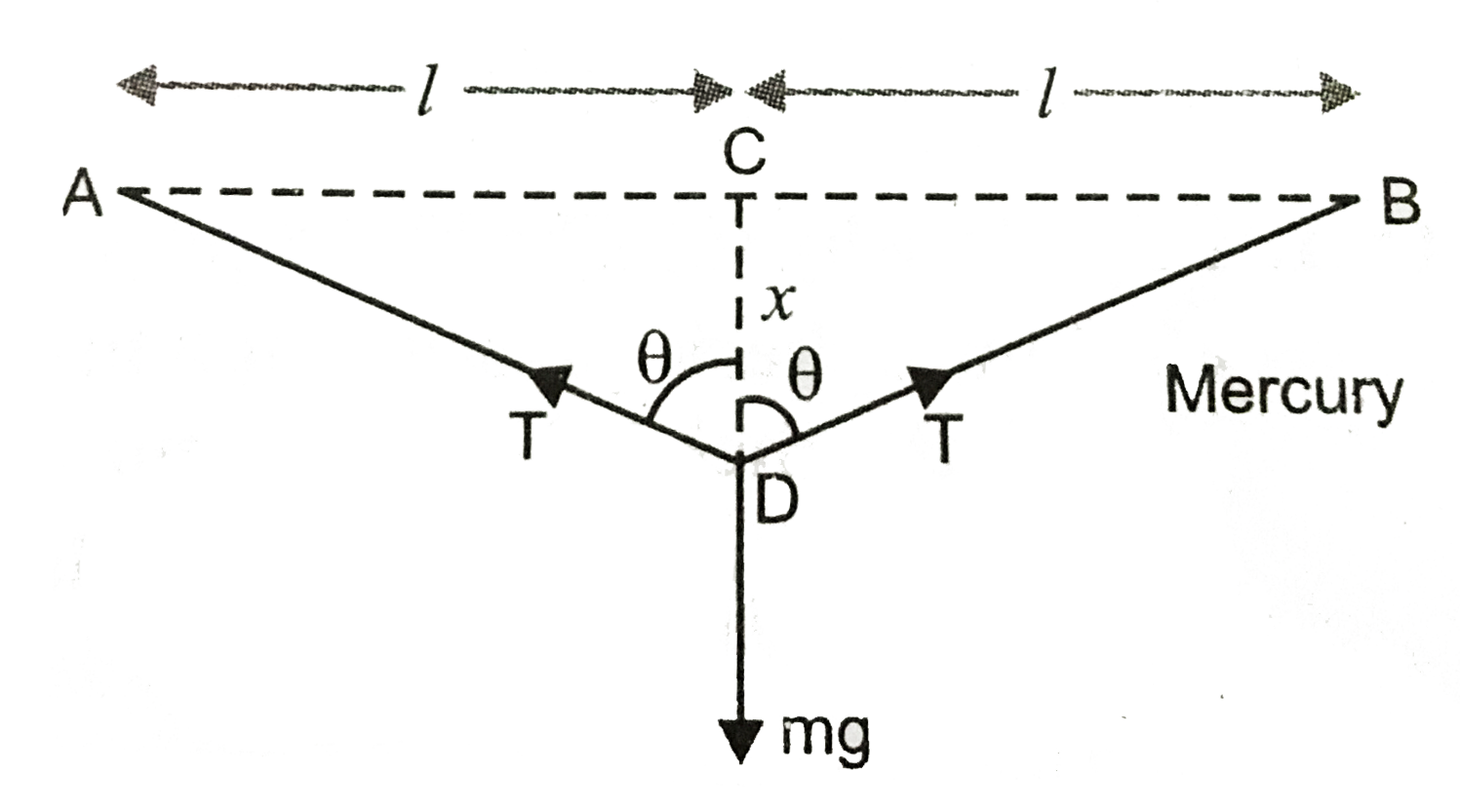
View SolutionTwo strips of metal are riveted together at their ends by four rivets, each of diameter 6mm. What is the maximum tension that can be exterted by the riveted strip if the shearing stress on the rivet is not to exceed `6.9 xx 10^(7) Pa`? Assume that each rivet is to carry one quarter of the load .
View SolutionThe marina Trench is located in the pacific ocean, and at one place it is nearly eleven km beneath the surface of water. The water pressure at the bottom of the Trench is about `1.1 xx 10^(8) Pa`. A steel ball of initial volume `0.32 m^(3)` is dropped into the ocean and falls to the bottom of the Trench. what is the change in the volume of the ball when it reaches to the bottom? Bulk modulus for steel =`1.6 xx 10^(11) Nm^(-2)`.
View SolutionExplain why (a) the blood pressure is humans is greater at the feet than at the brain.
(b) Atmospheric pressure at a height of about 6 km decreases to nearly half its value at the sea level through the 'height' of the atmospheric is more than 100 km.
(c) Hydrostatic pressure is a scalar quantity even though pressure is force divded by area , and force is a vector.
View SolutionExplain why
(a). The angle of contact of mercury with galss is obtuse, while that of water with glass is acute.
(b). Water on a clean glass surface tends to spread out while mercury on the same surface tends to form drops. (Put differently, water wets glass while mercury does not).
(c). Surface tension of a liquid is independent of the area of the surface
(d). Water with detergent disolved in it should have small angles of contact.
(e). A drop of liquid under no external forces is always spherical in shape.
View SolutionFind in the blanks using the word (s) from the test appended with each statement.
(a) Surface tension of liquid generally …..with temperatures (increase//decreases).
(b) Viscosity of gases ….. With temperature, whereas viscosity of liquids ……with temperature. (increases//decreases)/
(c) For solids with elastic modulus of rigidity, the shearing force is proportional to .....while for fluids it is proportional to ....(shear strain//rate of shear strain).
(d) For a dluid in a steady flow, from .....(conservation of mass// Bernoulli's principle)
(e ) For the model of a plane in a wind tunnel, turbulence oc curs at a ...... speed for turbulence for an actual plane (greater//smaller)/
View SolutionExplain why
(a). To keep a piece of paper horizontal, you should blow over, not under, it
(b). When w try to close a water tap with our fingers, fast jets of water gush through the openings between our fingers
(c). The size of the needle of a syringe controls flow rate better than the thumb pressure exerted by a doctor while administering an injection
(d). A fluid flowing out of a small hole in a vessel results in a backward thrust on the vessel
(e). A spinning cricket ball in air does not follow a parabolic trajectory.
View SolutionA 50 kg. girl wearing high heel shoes balance on a single heel. The heel is circular with a diameter 1 cm. what is the pressure exerted by the heel on the horizontal floor?
View SolutionTorricelli's barometer used mercury. Pascal duplicated it using French wine of density `984 kg m^(-3)`. Determine the height of the wine column for normal atmospheric pressure.
View SolutionA vertical off-shore structure is built to withstand a a maximum stress of `10^(9)Pa`. Is the structure suitabel for putting upon top of an oil well in bombay high? Take the depth of the sea to be roughly 3 km, and ignore oceam currents.
View SolutionA hydraulic automobile lift is designed to lift cars with a maximum mass of 300 kg. the area of cross-section of the piston carrying the load is `425cm^(3)`. What maximum pressure would smaller piston have to bear?
View SolutionA U tube contains water and methylated spirts separated by mercury columns in the two arms are in level with 10.0cm of water in one arm and 12.5 cm of spirit in the other. What is the relative density of spirit?
View Solutionin previous question, if 15 cm of water and spirit each are further poured into the respective arms of the tube. Difference in the level of mercury in the two arms is (Take, relvative density of mercury = 13.6)
View SolutionCan Bernoulli's equation be used to describe the flow of water through a rapid in a river? Explain.
View SolutionDoes it matter if one uses gauge instead of absolute pressures in applying Bernoulli's equation. Explain.
View SolutionGlycerine flows steadily through a horizontal tube of length 1.5m and radius 1.0 cm. if the amount of glycerine collected per second at one end is `4.0 xx 10^(-3) kg s^(-1)`, what is the pressuer difference between the two ends of the tube? (density of glycerine = `1.3xx10^(3)kgm^(-3)` and viscosity of glycerine =`0.83Ns m^(-2)`).
View SolutionIn a test experiment on a model aeroplane in a wind tunnel, the flow speeds on the upper and lower surface of the wing are `70 ms^(-1) and 63 ms^(-1)` respectivley. What is the lift on the wing if its area is `2.5 m^(2)`? Take the density of air is `1.3 kg m^(-3)`.
View SolutionThe steady flow of (non-viscous) liquid. Which of the two figure is incorrect?why?
View SolutionThe cylinderical tube of a spray pump has a cross-section of `8.0cm^(2)` one end of which has 40 fine holes each of diameter 1.0mm. If the liquid flow inside the tube is 1.5 m per minute, what is the speed of ejection of the liquid through the holes?
View SolutionA U-shaped wire is dipped in a soap solution, and removed. A thin soap film formed between the wire and a light slider supports a weight of `1.5xx10^(-2)N` (which includes the small weigh of the slider). The length of the slider is 30cm. What is the surface tension of the film?
View SolutionFig, shown a thin film supporting a small weight = `4.5xx10^(-2)N`. What is the weight supported by a film of the same liquid at the same temperature in fig. explain your answer physically.
 .
.
View SolutionWhat is the pressure inside a drop of mercury of radius 3.0mm at room temperature? Surface tension of mercury at that temperature `(20^(@)C)` is `4.65xx10^(-1)Nm^(-1)`. The atmospheric pressure is `1.01xx10^(5)Pa`. Also give the excess pressure inside the drop.
View SolutionWhat is the excess pressure inside a bubble of soap solution of radius 5.00mm, given that the surface tension of soap solution at the temperature `(20^(@)C)` is `2.50xx10^(-2)Nm^(-1)`? If an air bubble of the same dimension were formed at a depth of 40.0 cm inside a container containing the soap solution (of relative density 1.20), what would be the pressure inside the bubble? (1atm. is 1.01 xx 10^(5)Pa`).
View SolutionA tank with a square base of area `1.0m^(2)` is divided by a vertical parition in the middle. The bottom of the partition has a small hinged door of area `20cm^(2)`. The tank is filled with water and an acid (of relative density 1.7) in the other, both to a height of `4.0m`. Compute to force necessary the force nec cessary to keep the door closed.
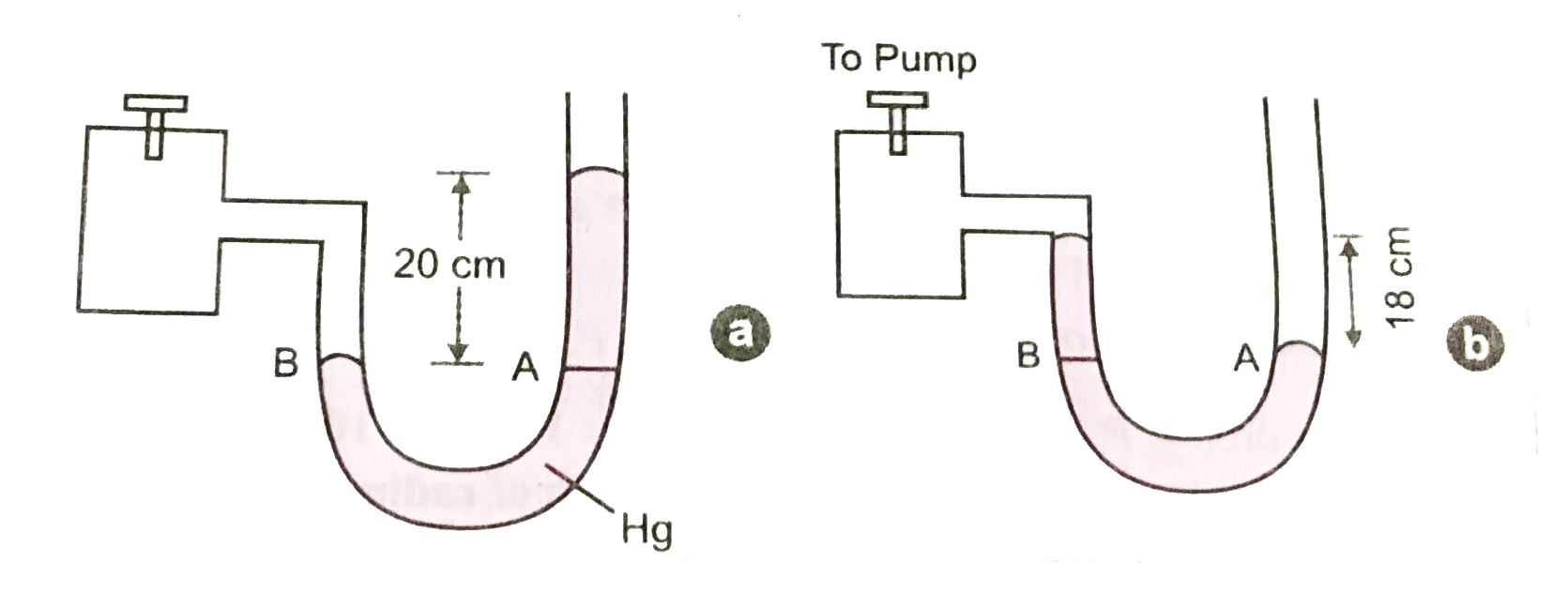
View SolutionA manometer reads the pressure of a gas in an encloure as shown in fig. when some of the gas is removed by the pump, the manometer reads as in fig. the liquid used in mano-meters is mercury and the atmospheric pressure is 76 cm of mercury.
(i) Given the absolute and gauge pressure of the gas in the two cases (in units of cm. of mercury).
(ii) How would the levels change in case(b) if `13.6cm` of water are poured into the right limb of manometer? (Ignore the change in volume of the gas).
View SolutionTwo vessels have the same base area but differnent shapes. The first vessel takes twice the vloume of water that the second vessel requires to fill up to a paricular common height . Is the force exerted by water on the base of the vessel the same in the two case? If so, why do the vessels filled with water to that same height give different reading on a weighting scale ?
View SolutionDuring blood transfusion the needle is inserted in a vein where the gauge pressure is `2000Pa` . At what height must the blood container be placed so that blood may just enter the vein? Density of whole blood = `1.06xx10^(3)Kg//m^(3)`.
View SolutionIn deriving Bernoulli's equation , we equated the workdone on the fluid in the tube to its change in the potential and kinetic energy (a) How does the pressure change as the fluid moves along the tube if dissipative forces are present ? (b) Do the dissipative forces becomes more important as the fluid velocity increase? Discuss qualitatively.
View Solution(a) What is the largest average velocity of blood flow in an artery of radius `2xx10^(-3)m` if the flow must remian laminar?
(b) What is the corresponding flow rate? Take viscosity of blood to be `2.084xx10^(-3)Pa-s`. Density of blood is `1.06xx10^(3)kg//m^(3)`.
View SolutionA plane is in level flight at constant speed and each of its wings has an area of `25m^(2)`. If the speed of the air is `180km//h` over the upper wing surface, determine the plane's mass . (Take air density to be `1 kg//m^(3)`). `g=9.8m//s^(2)`.
View SolutionIn Millikan's oil experiment, what is the terminal speed of a speed of a drop of radius `2.0 xx 10^(5)m` and density `1.2xx10^(3)m^(-3)`? Take the viscosity of air at the temperature of the expermental to be `1.8xx10^(-5)Nsm^(2)`. How much is the viscous force on the drop at that speed? Neglect buoyancy of the drop due to air.
View SolutionMercury has an angle of contact equal to `140^(@)` with soda lime galss. A narrow tube of radius `1.00mm` made of this glass is dipped in a through containing mercury. By what amount does the mercury dip down in the tube relative to the mercury surface outside? Surface tension of mercury at the temperature of the experiment is `0.465 Nm^(-1)`. Density of mercury = `13.6xx10^(3) kg m^(-3)`.
View SolutionTwo narrow bores of diameters 3.0mm and 6.0 mm are joined together to form a U-shaped tube open at both ends. If th U-tube contains water, what is the difference in its levels in the two limbs of the tube? Surface tension of water at the temperature of the experiment is `7.3xx10^(-2)Nm^(-1)`. Take the angle of contact to be zero. and density of water to be `1.0xx10^(3)kg//m^(3)`.
`(g=9.8 ms^(-2))`
View Solution(a). It is known that density `rho` of air decreases with height y as
`rho=rho_(0)e^(-y//y(_o))` ltb rgt where `p_(o)=1.25kgm^(-3)` is the density at sea level, and `y_(o)` is a constant. This density variation is called the law of atmospheres. Obtain this law assuming that the temperature of atmosphere remains a constant (isothermal conditions). Also assume that the value of g remains constant
(b). A large He balloon of volume `1425m^(3)` is used to lift a payload of 400 kg. Assume that the balloon maintains constant radius as it rises. How high does it rise?
[take `y_(o)=8000m and rho_(He)=0.18kgm^(-3)`]
View SolutionThe triple point of neon and carbon dioxide are `24.57K` and `216.55K` respectively. Express these temperature on the Celsius and Fahreaheit scales.
View SolutionTwo absolute scales `A` and `B` have triple points of water defined to be `200A` and `350B`. What is the relation between `T_(A)` and `T_(B)`?
View SolutionThe electrical resistance in ohms of a certain thermometer varies with temperature ac cording to the approximate law: `R =R_(0)[1+alpha(T-T_(0))]`
The resistances is `101.6 Omega` at the triple-point of water `273.16K`, and `165.5 Omega` at the normal melting point of lead `(600.5K)`. What is the temperature when the resistance is `123.4 Omega`?
View SolutionAnswer the following :
(a) The triple-point of water is a standard fixed point in modern thermometry. Why ? What is wrong in taking the melting point of ice and the boiling point of water as standard fixed points (as was originally done in the Celsius scale) ?
(b) There were two fixed points in the original Celsius scale as mentioned above which were assigned the number `0^(@)C" and "100^(@)C` respectively. On the absolute scale, one of the fixed points is the triple-point of water, which on the Kelvin absolute scale is assigned the number 273.16 K. What is the other fixed point on this (Kelvin) scale ?
(c ) The absolute temperature (Kelvin scale) T is related to the temperature `t_(c)` on the Celsius scale by
`t_(c)=T-273.15`
Why do we have 273.15 in this relation, and not 273.16 ?
(d) What is the temperature of the triple-point of water on an absolute scale whose unit interval size is equal to that of the Fahrenheit scale ?
View SolutionTwo ideal gas thermometer `A` and `B` use oxygen and hydrogen respectively . The following observations are made:
Temperature, Pressure therometer A, Pressure therometer B
Triple point of water, `1.250xx10^(5)Pa`, `0.200xx10^(5)Pa`
Normal melting point of sulphur, ` 1.797xx10^(5)Pa`, `0.287xx10^(5)Pa`
(a) What is the absolute temperature of normal melting point of sulphur as read by thermometers `A` and `B` ?
(b) What do you think is the reason for the slightly different answers from `A` and `B` ? (The thermometers are not faulty). what further procedure is needed in the experiment to reduce the discrepancy between the two readings.
View SolutionA steel tape 1m long is correctly calibrated for a temperature of `27^(@)C`. The length of a steel rod measured by this tape is found to be `63.0cm` on a hot day when the temperature is `45.0^(@)C`. What is the acutual length of the steel rod on that day? what is the length of the same steel rod on a day when the temperature is `27.0^(@)C` ? coefficient of linear expansion of steel ` = 1.20xx10^(-5) .^(@)C^(-1)`.
View Solutiona large steel wheel is to be fitted on to a shaft of the same material. At `27^(@)C`, the outer diameter of the shaft is `8.70cm` and the diameter of the central hole in the wheel is `8.69cm` . The shaft is cooled using 'dry ice' , At what temperature of the shaft does the wheel slip on the shaft? Assume coefficient of linear expansion of the steel to be constant over the required temperature range: `alpha_(steel) = 1.20xx10(-5)K^(-1)`.
View SolutionA hole is drilled in a copper sheet. The diameter of the hole is `4.24 cm` at `27.0^(@)C`. What is the change in the diameter of the hole when the sheet is heated to `227^(0)C`? `alpha` for copper `= 1.70 xx 10^(-5)K^(-1)`
View SolutionA brass wire `1.8 m` long at `27^(@)C` is held taut with little tension between two rigid supports. If the wire cooled to a temperature of `-39^(@)C`, what is the tension developed in the wire, if its diameter is `2.0 mm`? Coefficient of linear expansion of brass `= 2.0 xx 10^(-5)//^(@)C`, Young's modulus of brass `= 0.91 xx 10^(11) Pa`.
View SolutionA brass rod length 50 cm and diamteer 3.0 mm is joined to a steel rod of the same length and diameter. What is the change in length of the combined rod at `250^(@)C` if the original length are at `40^(@)C` ? Coefficient of linear expansion of brass and steel are `2.10xx10^(-5) .^@C^(-1)` and `1.2 xx 10^(-5) ^(@)C^(-1)` respectively.
View SolutionThe coefficient of volume expansion of glycerine is `49 xx 10^(-5)//^(@)C`. What is the fractional change in its density (approx.) for `30^(@)C` rise in temperature?
View SolutionA `10 kW` drilling machine is used to drill a bore in a small aluminium block of mass `8.0 kg`. How much is the rise in temperature of the block in `2.5` minutes, assuming `50%` of power is used up in heating the machine itself or lost to the surrounding? Specific heat of aluminium `= 0.91 J//g^(@)C`.
View SolutionA copper block of mass `2.5 kg` is heated in a furnace to a temperature of `500^(@)C` and then placed on a large ice block. What is the maximum amount (approx.) of ice that can melt? (Specific heat copper `= 0.39 J//g^(@)C` heat of fusion of water `= 335 J//g`).
View SolutionIn an experiment to determine the specific heat of a metal,a `0.20 kg` block of the metal at `150 .^(@) C` is dropped in a copper calorimeter (of water equivalent `0.025 kg`) containing `150 cm^3` of water at `27 .^(@) C`. The final temperature is `40.^(@) C`. The specific heat of the metal is.
View SolutionAnswer the following question beased on tbhe P-T phase diagram of carbon dioxide.

(a) At what temperature and pressure can the solid, liquid and vapour phases of `CO_2` co-exist is equilibrium ? (b) What is the effect of decrease of pressure on the fusion and bolling point of `CO_2` ? (c ) What are the critical temperature and pressure for `CO_2` ? What is their significane ? (d) Is `CO_2` solid, liquid or gas at (a) ` -70^@C` under 1 atm, (b) `-60^@C` under 10 atm, (c) `15^@C` under 56 atm ?
View SolutionAnswer the following questions based on the P – T phase diagram of `CO_(2)`:
(a) `CO_(2)` at 1 atm pressure and temperature` – 60^(@)C` is compressed isothermally. Does it go through a liquid phase ?
(b) What happens when `CO_(2)` at 4 atm pressure is cooled from room temperature at constant pressure ?
(c) Describe qualitatively the changes in a given mass of solid `CO_(2)` at 10 atm pressure and temperature `–65^(@)C` as it is heated up to room temperature at constant pressure.
(d) `CO_(2)` is heated to a temperature `70^(@)C` and compressed isothermally. What changes in its properties do you expect to observe ?
View SolutionA child running a temperature of `101^F` is given and antipyrin (i.e. a madicine that lowers fever) which cause an increase in the rate of evaporation of sweat from his body. If the fever is brought down to `98^@F` in 20 min., what is the averatge rate of extra evaporation caused, by the drug ? Assume the evaporation mechanism to the only way by which heat is lost. The mass of the child is 30 kg. The specific heat of human body is approximately the same as that of water and latent heat of evaporation of water at that temperature is about `580 cal. g^(-1).`
View SolutionA cubical thermocol ice box of side length `30cm` has thickess of `5.0cm` If `4.0kg` of ice is put in the box estimate the amount of ice remaining after `6hr` The outside temperature is `45^(@)C` and co-efficient of the thermal conductivity of the thermocol is `0.01 J s^(-1) m^(-1) K^(1)` (Latent Heat of fusion of water `=335 xx 10^(3) Jkg^(-1))` .
View SolutionA brass boiler has a base area of `0.15 m^2` and thickness 1.0 cm it bolis water at the rate of 6.0 kg/min, when placed on a gas stove. Estimate the temperature of the part of the flame in contact with the bolier. Thermal conductivity of brass ` =609 J s^(-1) .^@C^(-1).` Heat of vaporisation of water ` =2256 xx 10^3 J g^(-1)`
View SolutionExplain why : (a) A body with large reflectivity is a poor emitter. (b) A brass tumbler feels much colder then a wooden tray on a chilly day. (c ) an optical pyrometer (for measuring high temperatures) calibrated for an ideal black body correct value for the temperature when the same piece is in the furnace. (d) The earth without its atmosphere would be inshospitably cold. (e ) Heating system based on circulation of steam are more effecient in warming a building than those based on circulation of hot water.
View SolutionA body cools from `80^(@)C` to `50^(@)C` in 5 min-utes Calculate the time it takes to cool from `60^(@)C` to `30^(@)C` The temperature of the surroundings is `20^(@)C` .
View Solution
NCERT Questions questions and complete solutions for chapter PROPERTIES OF BULK MATTER of PRADEEP PHYSICS (HINGLISH) of Class 11
All Exercises from PRADEEP Class 11 PHYSICS PROPERTIES OF BULK MATTER
- Advanced problems for competitions
- Asseration - Reason Type Question
- Conceptual Problems
- Curiosity Questions
- Fill in the Blanks A
- Fill in the Blanks B
- Fill in the Blanks C
- Fill in the Blanks D
- Fill in the Blanks E
- Higher Order thinking skells
- Integer Type Questions
- Long Answer questions
- Multiple choice questions
- Multiple choice questions-I
- Multiple choice questions-II
- NCERT Questions
- Problmes for Practice
- Sample problem
- Short Answer Questions
- Solved Examples
- Test Your Grip A
- Test Your grip B
- Test Your Grip C
- Test Your Grip D
- Test Your Grip E
- Value Based Question
- Very short answer questions