Complete Solutions to JEE Main And Advanced of chapter SIMPLE HARMONIC MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SIMPLE HARMONIC MOTION |
| SUNIL BATRA | JEE Main And Advanced |
| Number Of Questions | 69 |
| Academic Year | 2023-24 |
An object of mass `0.2 kg` executes simple harmonic oscillation along the `x - axis`with a frequency of `(25//pi) Hz`. At the position `x = 0.04`, the object has Kinetic energy of `0.5 J` and potential energy `0.4 J. The amplitude of oscillations is……m.
View SolutionTwo bodies M and N of equal masses are suspended from two separate massless springs of spring constants `k_1` and `k_2` respectively. If the two bodies oscillate vertically such that their maximum velocities are equal, the ratio of the amplitude of vibration of M to the of N is.
View SolutionA particle free to move along the (x - axis) hsd potential energy given by `U(x)= k[1 - exp(-x^2)] for -o o le x le + o o`, where (k) is a positive constant of appropriate dimensions. Then.
View SolutionThe period of oscillation of a simple pendulum of length (L) suspended from the roof of a vehicle which moves without friction down an inclined plane of inclination (prop), is given by.
View SolutionA particle executes simple harmonic motion between `x = -A and x = + A`. The time taken for it to go from 0 to `A//2` is `T_1` and to go from `A//2` to (A) is `T_2`. Then.
View SolutionFor a particle executing (SHM) the displacement (x) is given by `(x = A) cos (omega) t`. Identify the graph which represents the variation of potential energy (PE) as a function of time (t) and displacement (x).
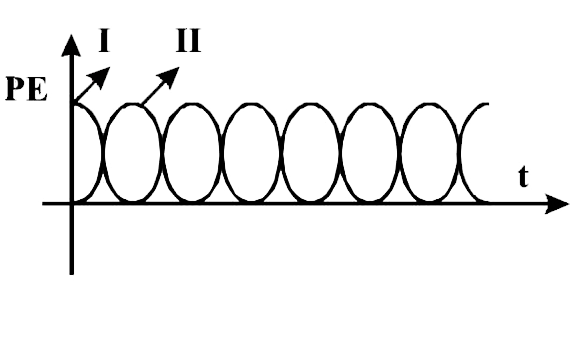 ,
, 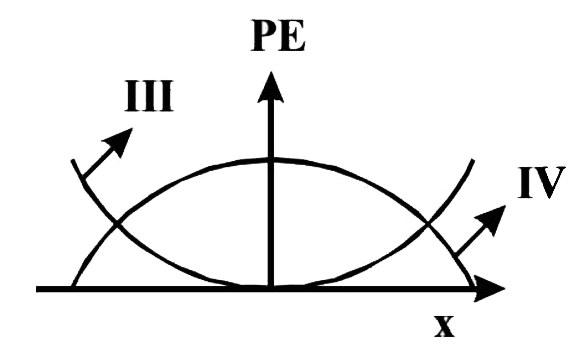 .
.
View SolutionA simple pendulum has time period `T_1`. The point of suspension is now moved upward according to the relation `y = K t^2, (K = 1 m//s^2)` where (y) is the vertical displacement. The time period now becomes `T_2`. The ratio of `(T_1^2)/(T_2^2)` is `(g = 10 m//s^2)`.
View SolutionThe (x - t) graph of a particle undergoing simple harmonic motion is shown below. The acceleration of the particle at `t = 4//3 s` is
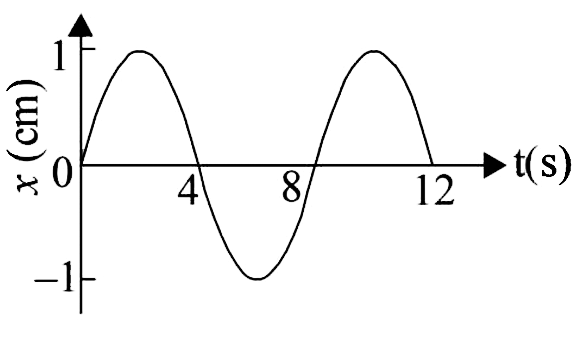 .
.
View SolutionA uniform rod of length L and mass M is pivoted at the centre. Its two ends are attached to two springs of equal spring constants k. The springs are fixed to rigid supports as shown in the figure, and the rod is free to oscillate in the horizontal plane. The rod is free to oscillate in the horizontal plane. The rod is gently pushed through a small angle `(theta)` in one direction and released. The frequency of oscillation is. ?
 .
.
View SolutionThe mass M shown in the figure oscillates in simple harmonic motion with amplitude A .The amplitude of the point P is
 .
.
View SolutionA point mass is subjected to two simultaneous sinusoidal displacements in `x - direction, x_1 (t) = A sin (omega)t and x_2 (t) = A sin ((omega t + (2 pi)/(3))`. Adding a third sinusoidal displacement `x _3 (t) = B sin (omega t + phi)` brings the mas to a complete rest. The values of (B) and (phi) are.
View SolutionA small block is connected to one end of a massless spring of un - stretched length `4.9 m`. The other end of the spring (see the figure) is fixed. The system lies on a horizontal frictionless surface. The block is stretched by `0.2 m` and released from rest at `t = 0`. It then executes simple harmonic motion with angular frequency `(omega) = (pi//3) rad//s`. Simultaneously at `t = 0`, a small pebble is projected with speed (v) from point (P) at an angle of `45^@` as shown in the figure. Point (P) is at a horizontal distance of `10 m from O`. If the pebble hits the block at `t = 1 s`, the value of (v) is `(take g = 10 m//s^2)`.
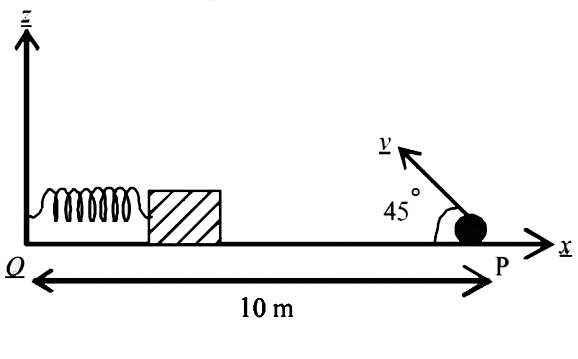 .
.
View SolutionA particle executes simple harmonic motion with a frequency f. The frequency with which its kinetic energy oscillates is
View SolutionA linear harmonic oscillator of force constant `2 xx 10^6 N//m` and amplitude (0.01 m) has a total mechanical energy of (160 J). Its.
View SolutionA uniform cylinder of length (L) and mass (M) having cross sectional area (A) is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half - submerged in a liquid of density (rho) at equilibrium position. When the cylinder is given a small downward push and released it starts oscillating vertically with small amplitude. If the force constant of the spring is (k), the prequency of oscillation of the cylindcer is.
View SolutionA highly rigid cubical block A of small mass `M` and slide `L` is fixed rigidly on to another cubical block B of the same dimensions and of low modulus of rigidity `η` such that the lower face of A completely covers the upper face of B. The lower face of B is rigidly held on a horizontal surface. A small force `F` is applied perpendicular to one of the sides faces of A. After the force is withdrawn, block A executes small oscillations the time period of which is given by.
View SolutionOne end of a long metallic wire of length (L) is tied to the ceiling. The other end is tied to a massless spring of spring constant . (K.A) mass (m) hangs freely from the free end of the spring. The area of cross- section and the Young's modulus of the wire are (A) and (Y) respectively. If the mass is slightly pulled down and released, it will oscillate with a time period (T) equal to :
View SolutionA particle of mass (m) is executing oscillations about the origin on the (x) axis. Its potential energy is `V(x) = k|x|^3` where (k) is a positive constant. If the amplitude of oscillation is a, then its time period (T) is.
View SolutionThree simle harmionic motions in the same direction having the same amplitude (a) and same period are superposed. If each differs in phase from the next by `45^@`, then.
View SolutionThe function `x = A sin^2 (omega)t + B cos^2 (omega)t + Csin (omega)t cos (omega)t` represent (SHM) for which of the option(s).
View SolutionA metal rod of length 'L' and mass 'm' is pivoted at one end. A thin disc of mass 'M' and radius R `ltL` is attached at its center to the free end of the rod. Consider two ways the disc is attached : (case A). The dise is not free to rotate about its centre and (case B) the disc is free to rotate about its centre. The rod disc system perfoms (SHM) in vertical plane after being released from the same displacement position. Which of the following statement (s) is (are) true ?
 .
.
View SolutionTwo independent harmonic oscillators of equal mass are oscillating about the origin with angular frequencies `(omega_1) and (omega_2)` and have total energies `E_1 and E_2`, respectively. The variations of their momenta (p) with positions (x) are shown (s) is (are).
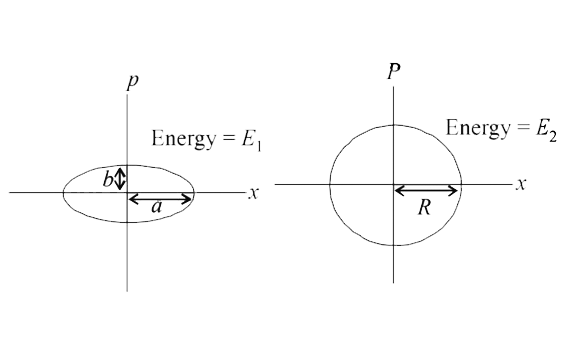
View SolutionA block with mass (M) is connected by a massless spring with stiffness constant (k) to a rigid wall and moves without friction on a horizontal surface. The block oscillates with small amplitude A about an equilibrium position (x_0). Consider two cases : (i) when the block is at (x_0) , and (ii) when the block is at `x = x_0 + A`. In both the cases, a particle with mass m(lt M) is softly placed on the block after which they strick to each other. Which of the following statement (s) is (are) true about the motion after the mass (m) is placed on the mass (M) ?
View SolutionA mass (M) attached to a spring, oscillates with a period of (2 sec). If the mass in increased by (2 kg) the period increases by one sec. Find the initial mass (M) assuming that Hook's Law is obeyed.
View SolutionTwo masses (m_1) and (m_2) are suspended together by a massless spring of spring constant (k). When the masses are in equilibrium, (m_1) is removed without disturbing the system. Find the angular frequency and amplitude of oscillation of (m_2).
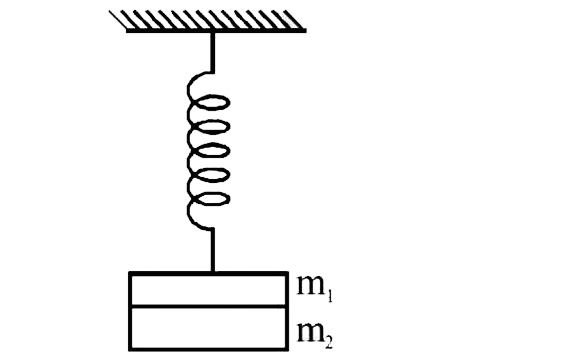 .
.
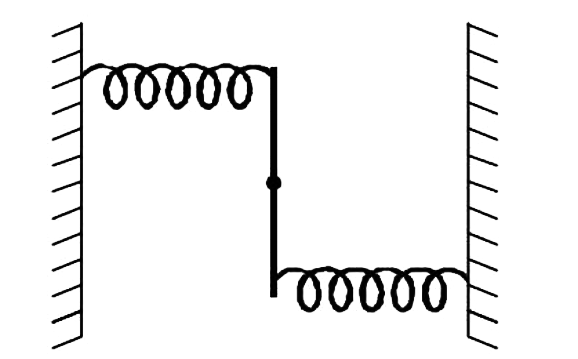
View SolutionTwo light springs of force constants `(k_1 and k_2)` and a block of mass (m) are in one line (AB) on a smooth horizontal table such that one end of each spring is fixed on rigid supports and the other end is free as shown in the figure. The distance (CD) between the free ends of the springs is (60 cms). If the block moves along (AB) with a velocity (120 cm//sec) in between the springs, calculate the period of oscillation of the block `k_1 = 1.8 N//m, k_2 = 3.2 N//m, m = 200 gm)`.
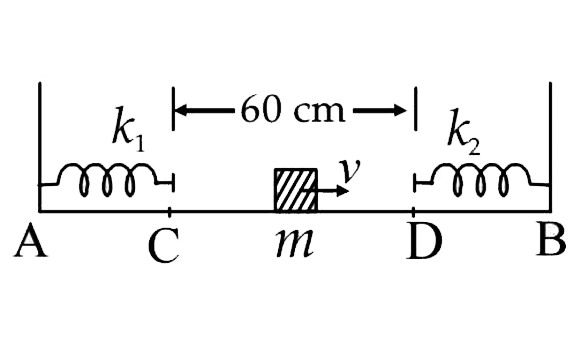 .
.
View SolutionTwo non - viscous, incompressible and immiscible liquids of densities (rho) and (1.5 rho) are poured into the two limbs of a circular tube of radius ( R) and small cross section kept fixed in a vertical plane as shown in fig. Each liquid occupies one fourth the cirumference of the tube.
 .
.
(a) Find the angle (theta) that the radius to the interface makes with the verticles in equilibrium position.
(b) If the whole is given a small displacement from its equilibrium position, show that the resulting oscillations are simple harmonic. Find the period of these oscillations.
View SolutionTwo identical balls (A) and (B) each of mass (0.1 kg), are attached to two identical massless springs. The spring - mass system is constrained to move inside a riged smooth pipe bant in the form of a circle as shown in Fig. The pipe is fixed in a horizontal plane.
The centres of the balls can move in a circle of radius (0.06 pi) meter. Each spring has a natural length z of `0.06 pi` meter and spring spring constant5 `0.1 N//m`. Initially, both the balls are displaced by an angle `theta = pi// 6` radian with respect to the diameter (pQ) of the circle (as shown in Fig.) and released from, rest.
 .
.
(i) Calculate the frequency of oscillation of ball (B).
(ii) Find the speed of ball (A) when (A) and (B) are at the two ends of the diameter (PQ).
(iii) What is the total energy of the system.
View SolutionA thin rod of length (L) and area of cross - section (S) is pivoted at its lowest point (P) inside a stationary, homegeneous and non - viscous liquid. The rod is free to ratate in a vertical plane about a horizontal axis passing through (P). The density (d_1) of the material of the rod is smaller than the density (d_2) of the liquid. The rod is displaced by a small angle (theta) from its equilibrium position and then released. Show that the motion of the rod is simple harmonic and determine its angular frequency in terms of the given parameters.
 .
.
View SolutionA small body attached to one end of a vertically hanging spring is performing (SHM) about is mean position with angular frequency (omega) and amplitude (a). If at a height (y*) from the mean position, the body gets detached from the spring, calculate the value of (y*) so that the height (H) attained by the mass is maximum. The body does noy interact with the spring during its subsquent motion after detachment. `(a omega^2 gt g)`.
 .
.
View SolutionWhen a particle of mass m moves on the x-axis in a potential of the form `V(x) =kx^(2)` it performs simple harmonic motion. The correspondubing time period is proprtional to `sqrtm/h`, as can be seen easily using dimensional analusis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of `x=0` in a way different from `kx^(2)` and its total energy is such that the particle does not escape toin finity. Consider a particle of mass m moving on the x-axis. Its potential energy is `V(x)=ax^(4)(agt0)` for |x| neat the origin and becomes a constant equal to `V_(0)` for |x|impliesX_(0)` (see figure).
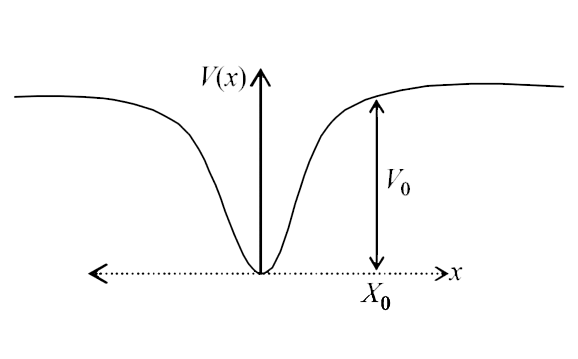
If total energy of the particle is E, it will perform perildic motion only if.
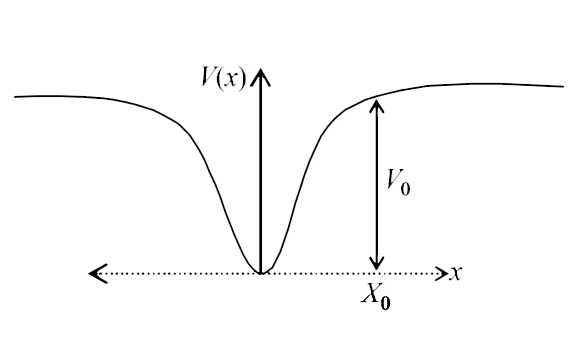
View SolutionWhen a particle of mass m moves on the x-axis in a potential of the form `V(x) =kx^(2)` it performs simple harmonic motion. The correspondubing time period is proprtional to `sqrtm/h`, as can be seen easily using dimensional analusis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of `x=0` in a way different from `kx^(2)` and its total energy is such that the particle does not escape toin finity. Consider a particle of mass m moving on the x-axis. Its potential energy is `V(x)=ax^(4)(agt0)` for |x| neat the origin and becomes a constant equal to `V_(0)` for |x|impliesX_(0)` (see figure).
 .
.
For periodic motion of small amplitude A,the time period (T) of thes particle is proportional to.
View SolutionWhen a particle of mass m moves on the x-axis in a potential of the form `V(x) =kx^(2)` it performs simple harmonic motion. The correspondubing time period is proprtional to `sqrtm/h`, as can be seen easily using dimensional analusis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of `x=0` in a way different from `kx^(2)` and its total energy is such that the particle does not escape toin finity. Consider a particle of mass m moving on the x-axis. Its potential energy is `V(x)=ax^(4)(agt0)` for |x| neat the origin and becomes a constant equal to `V_(0)` for `|x|impliesX_(0)` (see figure).
 .
.
The acceleration of this partile for `|x|gtX_(0)` is
(a) proprtional to `V_(0)`
(b) proportional to.
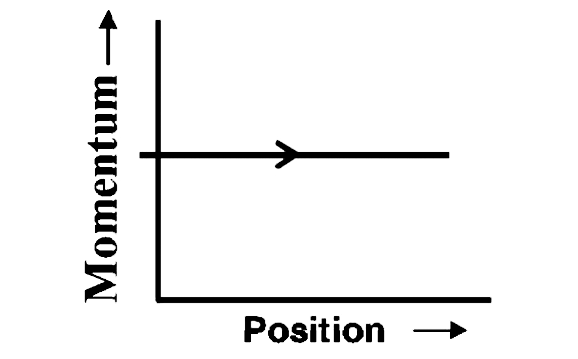
View SolutionPhase space deagrams are useful tools
 .
.
in analyzing all kinds of dynamical problems. They are especially usrful in studying the changes in motion as initial position and momenum are changed. Here we conseder some simple dynamical systems in one dimension. For such systems, phase space is a plane in which position is plotted along horizontal axis and momentum is plotted along vertical axis. The phase space diagram is `x(t) vs. p(t) curve in this plane. The arrow on the curve indicates the time flow. For example, the phase space diagram for a particle moving with constant velocity is a straight line as shown in the figure. We use the sign convention in which positon or momentum upwards (or to right) is poitive and downwards (or to left) is negative.
The phace diagram for a ball thrown vertically up from ground is.
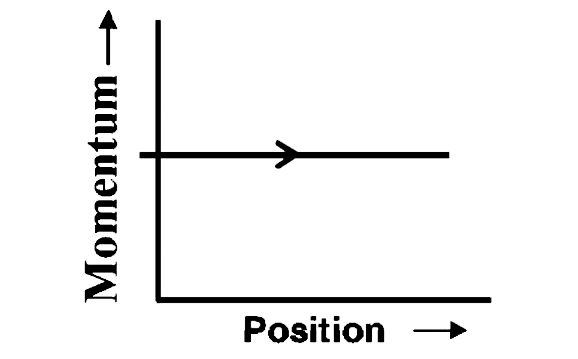
View SolutionPhase space deagrams are useful tools
 .
.
in analyzing all kinds of dynamical problems. They are especially usrful in studying the changes in motion as initial position and momenum are changed. Here we conseder some simple dynamical systems in one dimension. For such systems, phase space is a plane in which position is plotted along horizontal axis and momentum is plotted along vertical axis. The phase space diagram is `x(t) vs. p(t) curve in this plane. The arrow on the curve indicates the time flow. For example, the phase space diagram for a particle moving with constant velocity is a straight line as shown in the figure. We use the sign convention in which positon or momentum upwards (or to right) is poitive and downwards (or to left) is negative.
The plase space deagram for simple harmonic motion is a circle centered at the origin. In the figure, the two circles represent the same oscillator but for different initial condetions, and E_(1) and E_(2) the total mechanical energies respectivey.
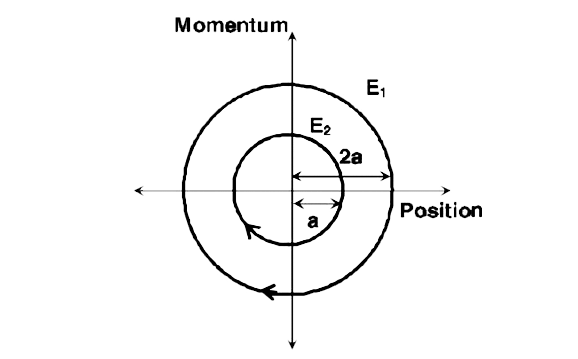 .
.
View SolutionPhase space deagrams are useful tools
 .
.
in analyzing all kinds of dynamical problems. They are especially usrful in studying the changes in motion as initial position and momenum are changed. Here we conseder some simple dynamical systems in one dimension. For such systems, phase space is a plane in which position is plotted along horizontal axis and momentum is plotted along vertical axis. The phase space diagram is `x(t) vs. p(t) curve in this plane. The arrow on the curve indicates the time flow. For example, the phase space diagram for a particle moving with constant velocity is a straight line as shown in the figure. We use the sign convention in which positon or momentum upwards (or to right) is poitive and downwards (or to left) is negative.
Consider the spring-mass system, with mass submerged in water, as shown in the figure. The phase space diagram for one cycle of this system is.
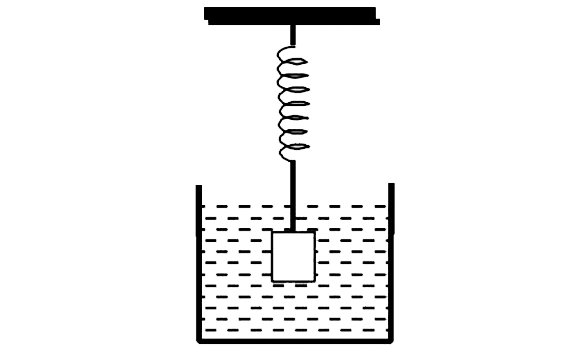 .
.
View SolutionIn a simple harmonic oscillator, at the mean position
View SolutionIf a spring has time period T, and is cut into n equal parts, then the time period of each part will be.
View SolutionA child swinging on a swing in sitting position, stands up, then the time period of the swing will.
View SolutionA mass (M) is suspended from a spring of negligible mass. The spring is pulled a little and then released so that the mass executes SHM of time period T. If the mass is increased by m, the time period becomes `(5T)/3`. Then the ratio of `m/M` is .
View SolutionTwo particles (A) and (B) of equal masses are suspended from two massless spring of spring of spring constant `k_(1)` and `k_(2)`, respectively, the ratio of amplitude of (A) and (B) is.
View SolutionThe length of a simple pendulum executing simple harmonic motion is increased by `21%`. The percentage increase in the time period of the pendulum of increased length is
View SolutionThe disperod of a particle varies according to the relation `x=4 (cos pit+ sinpit)`. The amplitude of the particle is.
View SolutionA body executes simple harmonic motion. The potential energy (P.E), the kinetic energy (K.E) and energy (T.E) are measured as a function of displacement `x`. Which of the following staements is true?
View SolutionThe bob of a simple pendulum executm simple harmonic motion in water with a period t, while the period of oscillation of the bob is `t_(0)` in air. Negleting frictional force of water and given that the density of the bob is (4//3)xx1000 kg//m^(3).
What relationship between t and `t_(0)` is true.
View SolutionA particle at the end of a spring executes S.H,M with a period `t_(2)` If the period of oscillation with two spring in .
View SolutionThe total energy of a particle, executing simple harmonic motion is.
where x is the displacement from the mean position, hence total energy is independent of x.
View SolutionA particle of mass (m) is attached to a spring (of spring constant k) and has a narural angular frequency omega_(0). An external force `R(t)` proportional to cos omegat(omega!=omega)(0) is applied to the oscillator. The time displacement of the oscillator will be proprtional to.
View SolutionIn forced oscillation of a particle the amplitude is maximum for a frequency `omega_(2)` of the force while the energy is maximum for a frequecyomega_(2) of the force, then .
View SolutionTwo simple harmonic are represented by the equation `y_(1)=0.1 sin (100pi+(pi)/3) and y_(2)=0.1 cos pit`.
The phase difference of the velocity of particle 1 with respect to the velocity of particle 2 is.
View SolutionThe function sin^(2) (omegat) represents.
View SolutionThe bob of a simple pendulum is a spherical hollow ball filled with water. A plugged hole near the bottom of the oscillating bob gets suddenly unplugged. During observation, till water is coming out, the time period of lscillation would.
View SolutionIf a simple harmonic motion is erpresented by `(d^(2)x)/(dt^(2))+ax=0`,
its time period is.
View SolutionThe maximum velocity a particle, executing simple harmonic motion with an amplitude 7 mm, 4.4 m//s. The period of oscillation is.
View SolutionStarting from the origin a body osillates simple harmonicall with a period of 2 s. A fter what time will its kinetic energy be 75% of the total energy?
View SolutionTwo springs, of force constants `k_(1)` and commected to a mass (m) as shown. The frequency of oscillation of the mass is (f). If both `K_(2) are made four times their original values, the frequency of oscillation becomes .
View SolutionA particle of mass m executes simple harmonic motion with amplitude a and frequency v. The average kinetic energy during its motion from the position of equilinrium to the end is.
View SolutionThe displacement of an obuect attached to a spring and executing simple harmonic motion is given by `x=2xx100^(-2) cos pit` metre. The time at which the maximum speed first occurs is.
View SolutionA point mass oscillates along the x-axis according to the law `x=x_(0) cos(moegat-pi//4). If the acceleration of the particle is written as `a=A cos(omegat+delta), the .
View SolutionIf x, and a denote the displacement, the velocity and the acceler of a particle executing simple harmonic motion of time period T, then, which of the following does not change with time?
View SolutionTwo particles are executing simple harmonic of the same amplitude (A) and frequency `omega` along the x-axis . Their mean position is separated by distance `X_(0)(X_(0)>A)`. If the maximum separation between them is `(X_(0)+A)`, the phase difference between their motion is:
View SolutionA mass (M), attached to a horizontal spring, executes S.H.M. whith amplitude `A_(1)`. When the mass (M) passes throgh its mean position then shaller mass (m) is placed over it and both of them move together with amplitude `A_(2)`. The ration of.
View SolutionIf a simple pendulum has significant amplitude (up to a factor of 1/e of original) only in the period between t = Os to `t = tau s`, then `tau` may be called the average life of the pendulum. When the spherical bob of the pendulum suffers a retardation (due to viscous drag) proportional to its velocity, with 'b' as the constant of proportionality, the average life time of the pendulum is (assuming damping is small) in seconds:
View SolutionThe amplitude of damped oscillator decreased to `0.9` times its original magnitude is `5s`. In another `10s` it will decrease to `alpha` times its original magnitude, where `alpha` equals.
View SolutionAn ideal gas enclosed in a vertical cylindrical container supports a freely moving piston of mass `M`. The piston and the cylinder have equal cross - section area `A`. When the piston is in equilibrium, the volume of the gas is `(V_0)` and the its pressure is `(P_0)`. The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, Show that the piston executes simple harmonic motion and find the frequency of oscillations.
View SolutionA particle moves with simple harmonic motion in a straight line. In first `taus`, after starting form rest it travels a destance a, and in next `tau s` it travels 2a, in same direction, then:
View SolutionA pendulumd made of a uniform wire of cross sectional area (A) has time T.When an additionl mass (M) is added to its bob, the time period changes to `T_(M). If the Young's modulus of the material of the wire is (Y) then `1/Y` is equal to:
View SolutionFor a simple pendulum, a graph is plotted its kinetic energy (KE) and potential energy (PE) against its displacement d. Which one of the following represents these correctly?
View SolutionA particle performs simple harmonic mition with amplitude A. Its speed is trebled at the instant that it is at a destance
`(2A)/3` from equilibrium position. The new amplitude of the motion is:
View Solution
JEE Main And Advanced questions and complete solutions for chapter SIMPLE HARMONIC MOTION of SUNIL BATRA 41 YEARS IITJEE PHYSICS (HINGLISH) of Class 11