Complete Solutions to EXAMPLE of chapter OSCILLATIONS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | OSCILLATIONS |
| AAKASH INSTITUTE | EXAMPLE |
| Number Of Questions | 21 |
| Academic Year | 2023-24 |
Categorize the motion as periodic or oscillatory motion
(I) Motion of planets around the sun.
(ii) A weighted test tube floating in a liquid pressed down and released
(ii) Motion of hands of a clock.
View SolutionA nurse in a hospital , noted for a patient that heart was beating 75 times a minutes. Find its frequency and time period.
View SolutionWhich of the following functions of time represented (a) periodic and (b) non-periodic motion ? Given the period for each case of periodic motion `( omega` is any positive constant(i)`sin omega t-cos omegat(ii) log ( 2 omega)`
View SolutionCategorise the following function of time `: sin omega t + sin 3 omega t + sin 5 omega t ` as
(a) S.H.M.
(b) Periodic but no S.H.M. .Also give the period.
Hint `:` Find the smallest interval of time after which the sum of 3 terms repeats
View SolutionCategories the following function of time `3 sin ( 2 omegat - (pi)/( 4))` as
(a) SHM , (b) Periodic but not SHM. Also give the period.
View Solution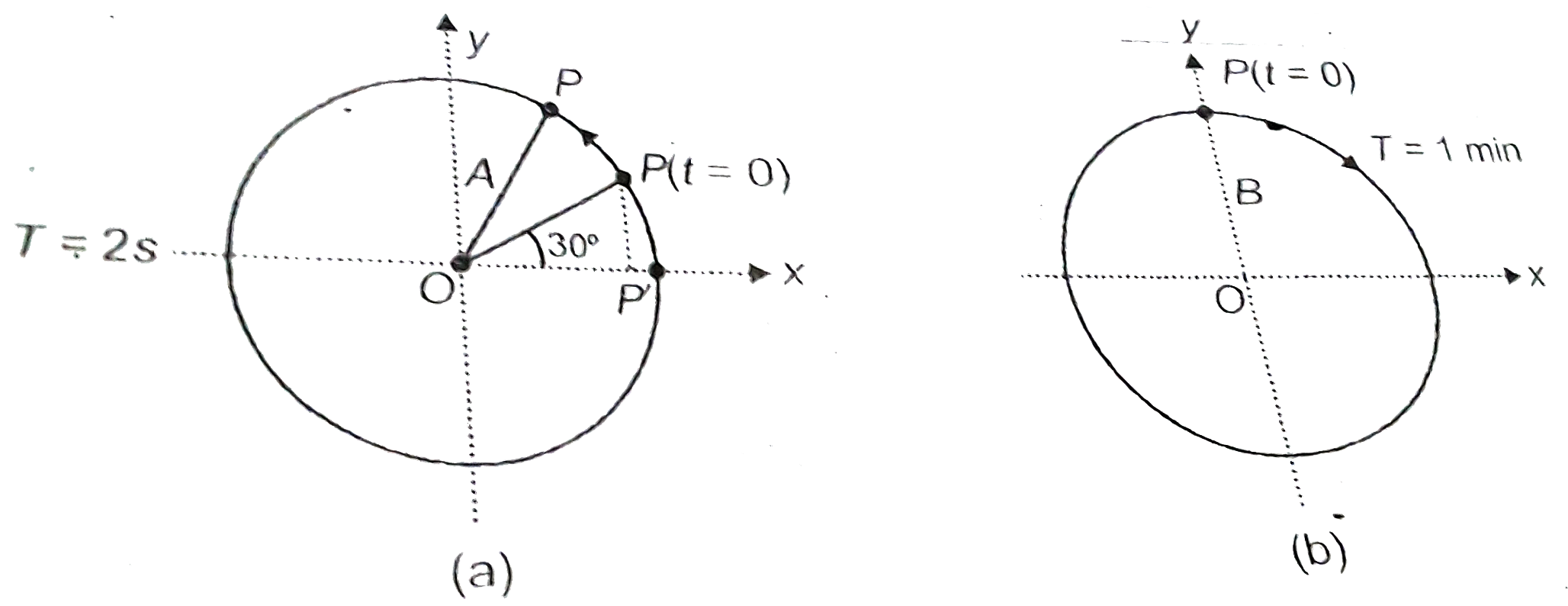
Figure depicts two circular motions. The radius of the circle, the period of revolution, the initial position and the sense of revolution are indicated on the figure. Obtain the SHMs of the x-projection of the radius vector of the rotating particle P in each case.
View SolutionIn the figure, dots and arrows show the position and the velocity of a paritcle executing SHM. What are the phases at the five indicated instants when the position at time t is given by
`x = Asin (omega t + phi)`

View SolutionPlot the corresponding reference circle for given SHM, indicate the initial `( t=0)` position of the paritcle, the radius of the circle , and the angular speed of the rotating paritcle. Consider anticlockwise direction for rotation. `x= - 3 sin ( 2 t + (pi)/(4))` (Express in the form , `x=` Acos ( omega t + phi))`.
View SolutionA particle executes a simple harmonic motion of time period T. Find the time taken by the particle to go directly from its mean position to half the amplitude.
View SolutionA particle executes SHM with a time period of 2s and amplitude 10 cm . Find its (i) Displacement (ii) Velocity (iii) Acceleration after 1/6 s, Starting from mean position.
View SolutionA particle of mass 2 kg executing SHM has amplitude 10 cm and time period is 1 s.Find (i) the angular frequency (ii) the maximum speed (ii) the maximum acceleration (iv) the maximum restoring force (v) the speed when the displacement from the mean position is 8 cm (vi) the speed after `(1)/(12)` s the particle was at the extreme position (vii) the time taken by the particle to go directly from its mean position to half the amplitude (viii) the time taken by the particle to go directly from its exterme position to half the amplitude.
View SolutionThe speed of a particle executing SHM with amplitude of displacement 5 cm is `3 cm //s ` at a distance 2.5 cm from mean position. What will be its speed at a distance `2.5 sqrt(3)` from mean position?
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in Fig. 14.14. Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find the period of oscillations.
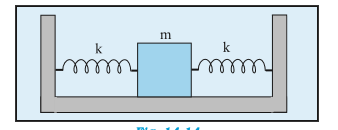
View SolutionHowdoes the huge ball `( 5.4 xx 10^(5) kg )` hanging on the `22^(nd)` floor of one of the world's tallest building ( chapter opening question mentioned in the introduction) counter the sway of the building?
View SolutionA block whose mass is 2 kg is fastened on a spring whose spring constant is 100 `Nm^(-1)` . It is pulled to a distance of 0.1 m from over a frictionless surface and is released at t=0. Calculate the kinetic eneryg of the block when it is 0.05 m away from its mean position.
View SolutionA particle executes SHM with amplitude A and time period T. When the displacement from the equilibrium position is half the amplitude , what fractions of the total energy are kinetic and potential energy?
View SolutionA particle of mass 0.2 kg is excuting SHM of amplitude 0.2 m. When it passes through the mean position its kinetic energy is `64 xx 10^(-3) J` . Obtain the equation of motion of this particle if the initial phase of oscillation is `pi//4`.
View SolutionA 2.5 kg collar is attached to a spring of spring constant `250 Nm^(-1)` . It slides without friction over a horizontal surface . It is displaced from its equilibrium position by 20 cm and releasd. Calculate the period of osciallation and the maximum speed.
View SolutionThe length of the simple pendulum which ticks seconds is
View SolutionIf the length of a simple pendulum of a clock incrreases by `2%` how much loss or gain of second per day will take place ?
View SolutionFor the damped oscillator shown in Figure, the mass m of the block is 400 g, `k=45 Nm^(-1)` and the damping constant b is `80 g s^(-1)`. Calculate .
(a) The period of osciallation ,
(b) Time taken for its amplitude of vibrations to drop to half of its initial value and
(c ) The time taken for its mechanical energy to drop to half its initial value.
View Solution
EXAMPLE questions and complete solutions for chapter OSCILLATIONS of AAKASH INSTITUTE ENGLISH of Class 12
All Exercises from AAKASH INSTITUTE Class 12 PHYSICS OSCILLATIONS
- ASSIGNMENT ( SECTION-E(ASSERTION-REASON TYPE QUESTION) )
- ASSIGNMENT (SECTION -D( Comprehension) )
- ASSIGNMENT (SECTION-B )
- ASSIGNMENT ( SECTION -A)
- ASSIGNMENT ( SECTION-C )
- ASSIGNMENT ( SECTION-F( MATRIX MATCH TYPE QUESTIONS) )
- ASSIGNMENT ( Section-G( Integers Answer Type Question) )
- ASSIGNMENT ( SECTION-H ( MULTIPLE TRUE-FALSE TYPE QUESTIONS) )
- ASSIGNMENT ( SECTION-I(SUBJECTIVE TYPE QUESTIONS) )
- ASSIGNMENT ( SECTION-J )
- Assignment (Section - A) (OBJECTIVE TYPE QUESTIONS)
- Assignment (Section - B) (OBJECTIVE TYPE QUESTIONS)
- Assignment (Section C) (PREVIOUS YEARS QUESTIONS)
- Assignment (Section D) (ASSERTION-REASON TYPE QUESTIONS)
- EXAMPLE
- EXAMPLE 1
- Exercise
- Try Yourself