Complete Solutions to Try Yourself of chapter OSCILLATIONS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | OSCILLATIONS |
| AAKASH INSTITUTE | Try Yourself |
| Number Of Questions | 86 |
| Academic Year | 2023-24 |
Categorize the motion as periodic or oscillatory motion
(i) Motion of Halley 's comet around the sun
(ii) Motion osf the penedulum of a wall clock
(iii) Motion of liquid n a U-tube when liquid is once compresed in one limb and then left to itself
Hint `:` In oscallatory motion, there is to and fro motion about some mean position.
View SolutionIs circular motion an exampleos oscillatory motion ?
Hint `:` Think - is there to and fro motion about some mean position which is the basic concept for oscillatory motion ?
View SolutionFrom the given graph , find time period and frequency for A and B.
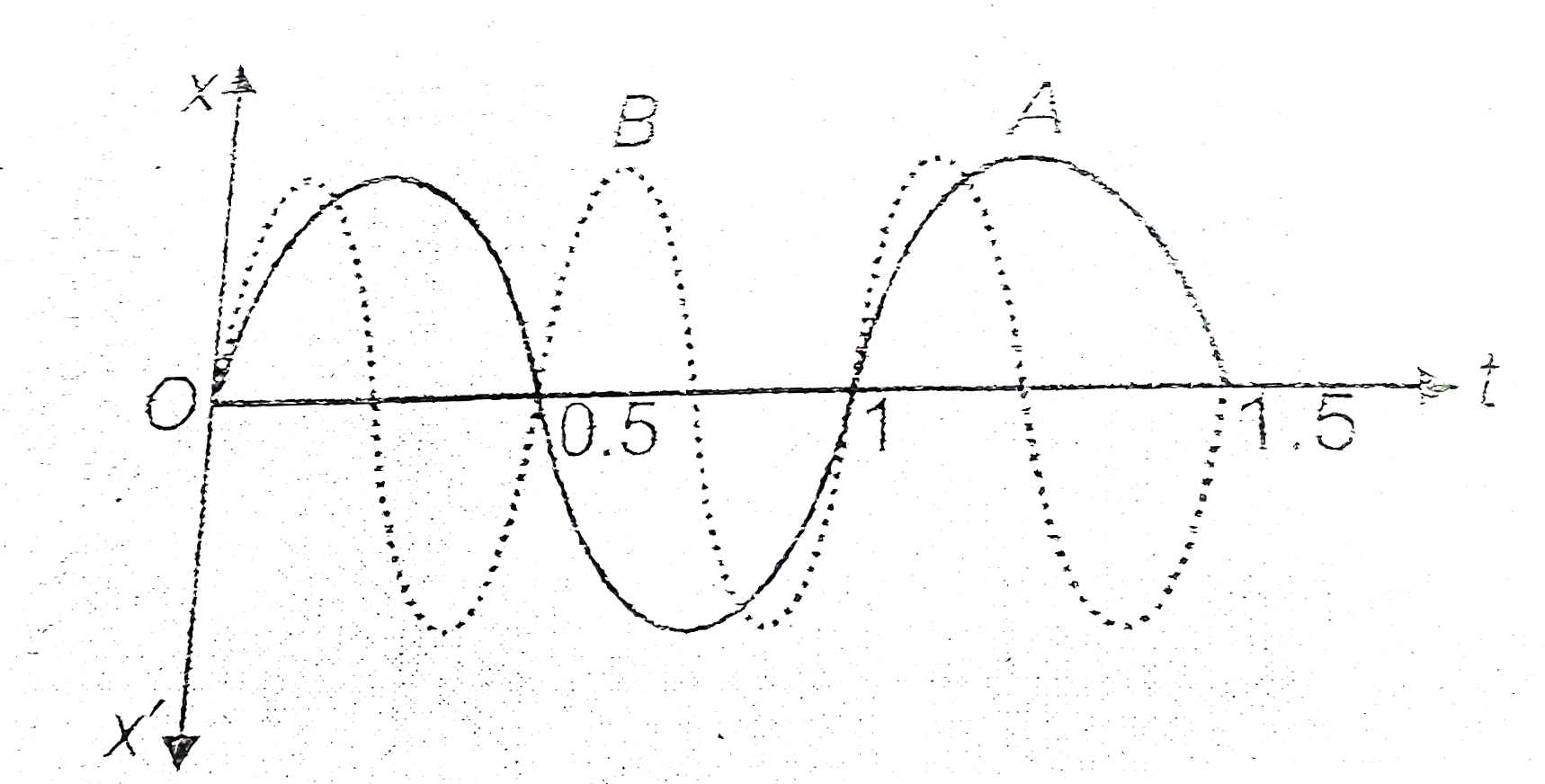
Hint `:` Find the time after which the motion is repeated . This gives time period T. Frequency `v= (1)/(T0`
View SolutionThe beat frequency of heart of a person is 1.35 H z. How many times, does it beat in a minute ? What is the time period ?
Hint `:` Number of oscillations in `1s =1.35`
Find number of oscillations in 60 s , and `T= (1)/(v)`
View SolutionDoes `cos omegat +sin2 omega t +cos 4 omega t ` represent periodic motion ? If yes, then find the period`( omega` is any positive constant) .
Hint `:` ( Each term represents a periodic function with different angular freuency . Find the smallest interval of time after which the sum of three terms repeats ) .
View SolutionDoes `e^(omegat)` represent periodic motion ? Ifyes, then find the period `( omega ` is any positive constant )
Hint `:` (Think , Does it repeat itself)
View SolutionCategorise the following function of time ` : cos^(2) omega t` as
(a) S.H.M.
(b) Periodic but not S.H.M. Also , give the period
Hint `: cos^(2) omegat = (1)/(2) + (1)/(2) cos 2 omegat`
View SolutionCategorise the following function of time `: cos^(3) omega t ` as
(a) S.H.M.
(b) Periodic but not S.H.M. Also find the period.
Hint `:` `cos^(3) omegat= (1)/(4)( 3 cos omegat- cos 3 omegat )`
View SolutionCategorise the following function of time `: sin omega t + sin 5 omega t ` as
(a) S.H.M.
(b) Periodic but no S.H.M. .Also give the period.
Hint `:` Find the smallest interval of time after which the sum of 2 terms repeats
View SolutionCategorise the following function of time `e^(omega^(2)t)` as
(a) S.H.M.
(b) Periodic but not S.H.M. Also , give period if it is periodic motion.
Hint `:` Doest it repeat itself ?
View SolutionObtain the equation of S.H.M. of a particle whose amplitude is 0.02,and whose frequency is 25 Hz. The initial phase is `(pi)/(4)`
Hint `: x= A sin ( omegat +phit)`
`omega = 2pi v`
View SolutionThe shortest distance travelled by a particle executing S.H.M. from mean position in 4 seconds is eual to `(1)/(sqrt(2))` times its amplitude. Find the time period.
Hint `: t=4 s , x = (1)/(sqrt(2)) , T=?`
`x = A sin omega t , omega = ( 2pi)/( T )`
Solve to get T.
View SolutionA harmonic osciallation is represented by `x=0.25 cos ( 6000t + 0.85)` ,where x and t are in mm and second respectively . Deduce (i) amplitude , (ii) frequency (iii) angular frequency
Hint `: ` Compare with `x= A cos ( omega t + phi)` a is amplitude frequency , `v = ( omega)/(2pi) , omega = 6000 rad s^(-1)`
View SolutionFor Question `x= 0.25 cos ( 6000 t + 0.85)` ,find (i) period and (ii) initial phase
View SolutionPlot the corresponding reference circle for given SHM `x = 2 cos ((pi)/(3) -t)` .Indicate the initial `( t- 0)` position of the particle , the radius of the circle and the angular speed of the rotating particle . Consider anticlockwise direction for rotation.
Hint `:` `x = 2 cos ((pi)/(3) -t)=2 cos ( t- (pi)/(3)) ` as ` cos ( - theta) = cos theta` . Compare with `x= A cos ( omegat + phi)`
View SolutionThe corresponding reference circle for a given SHM has been shown in the figure. Given `phi = ( 7pi)/(4)` . Write the corresponding equation of SHM. Consider anticlockwise direction for rotation.

Hint `: x= 2 cos ( 2pit+ (7pi)/( 4))`
`2 cos ((3pi)/( 2) + ( 2pit+(pi)/(4)))`
View SolutionFind the time taken by the particle in going from x = (A)/2) to `x=A` Hint :` Time taken to go from `x=0` to `x =A ` ` Time taken to go from x=0` to`x= (A)/(2)` Required time `= t_(1) - t_(2)`
View SolutionA particle startsits SHM at `t=0` . At a particular instant on its way to extreme position , `x= (A)/(2)` . Find the time taken by the particle to come back to this point after passing through the extreme position.
Hint `: t_(1) = ` time taken to go from `x=0` to `x= (A)/(2)`
`t_(2) =` time taken to go to extreme position and come back to mean position `= (T)/(2)`
Required time `= (T)/(2) - t_(1)`
View SolutionA particle executes SHM on a straight line path. The amplitude of oscialltion is 3 cm. Magnitude of its acceleration is eqal to that of its velocity when its displacement from the mean position is 1 cm. Find the time period of S.H.M.
Hint `: A= 3cm`
When`x=1 cm` , magnitude of velocity `=`magnitude of acceleration
i.e., `omega(A^(2) - x^(2))((1)/(2)) = omega^(2) x`
Find `omega`
`T = ( 2pi)(omega)`
View SolutionFor Question , find maximum velocity and maximum acceleration
Hint `:` Maximum velocity `= Aomega`
Maximum acceleration`= A omega^(2)`
A particle executes SHM on a straight line path. The amplitude of oscillation is 3cm . magnitude of its acceleration is equal to that of its velocity when its displacement from the mean position is 1cm.
View SolutionThe acceleration of a particle performing SHM is`12 cm //s^(2)` at a distance of 3 cm from the mean position . Calculate its time - period .
Hint `: a = omega^(2) x`
`a = 12 cm//s^(2) , x=3cm`
Find `omega`
`T= (pi)/(omega)`
View SolutionA particle executes simple harmonic motion about `x=0` along x-axis. The position of the particle at an instant is given by `x= ( 5 cm) sin pi t`. Find the average velocity and average acceleration for a time interval `0-0.5 s`.
Hint `:` Average velocity `=( x_(2)- x_(1))/(t_(2)-t_(1))`
`x_(1) = 5 sin 0`
`x_(2) = 5 sin ( pi xx 0.5)`
`t_(2) - t_(1) = 0.5`
Average acceleration `= ( v_(2) - v_(1))/( t_(2) - t_(1))`
`v=(dx)/(dt) = 5 pi cos pit`
`implies a _(av) = ( 5 pi cos ( pi xx 0.5) -5 pi cos theta)/(0.5)`
View SolutionIf maximum speed and acceleration of a particle executing SHM be `10 cm //s` and `100 pi cm//s^(2)` respectively ,then find its time period.
Hint `:v_("max") =A omega = 10`
`a_(max) = A omega^(2) = 100pi`
Solve to get `omega`
`T = ( 2pi)/( omega)`
View SolutionA particle of mass 2 kg is moving with SHM. Its greatest velocity is `40 ms^(-1)` and its amplitude is 20m. Find the time period and the force of attraction towards the centre when the particles is at its greates distance.
Hint `:` Maximum velocity ,`A omega = 40ms^(-1) ,A = 20 cm`, find `omega ` .
Then find `T= ( 2pi)/( omega)` Force of attractino towards centre `=` Restoring force `= m omega^(2) A`
View SolutionThe vertical motion of a huge piston in a machine is approximately SHM with a frequency of 1Hz.A block of mass 20 kg is placed on the piston . What is the maximum amplitude of the piston's SHM for the block and the piston to remain together .
Hint `:` `v= (1)/( 2pi)sqrt((k)/(m))`
Find k
For maximum displacement ` x_(max) =A`
For maximum restoring force , `F= - kA = -mg`
`:. A = (mg)/(k) = (mg) /( momega^(2))= (g)/( omega^(2))`
View SolutionThe vertical motion of a huge piston in a machine is approximately SHM. A block of 5 kg is placed on the piston. The maximum amplitude of the piston's SHM for the block and the piston to remains together is 0.99m. Find the frequency .
Hint `:` `v= (1)/( 2pi)sqrt((k)/(m))`
Find k
For maximum displacement ` x_(max) =A`
For maximum restoring force , `F= - kA = -mg`
`:. k= (mg)/( A)`. Put the valeu of K in `v =(1)/( 2pi ) sqrt((k)/(m))` to find v .
View SolutionMany builidings have other types of mass dampersas antisway devices ( Refers of Example 14) some like the Johns Honacock building in Boston,have a larger block oscillating at the end of spring and an a lubricated track. .Suppose the block has `m=5.44 xx 10^(5) kg` and is designed to oscillate at a frequency of`5 sqrt(2)` Hz and with amplitude ` x_(m) = 0.40 m` . Find the total mechanical energy E of the spring block system.
Hint `:K =m omega^(2) = m ( 2pi v ) ^(2)`
`E = K+U = (1)/(2) mv^(2) + (1)/(2) kx^(2)`
View SolutionFor Question , calculate the block's speed asit passes through the equilibrium point ?
View SolutionIf force constant = 100 N/m, find the potential energy of the block at 0.05 m from the mean position
Hint `: P.E. = (1)/(2) kx^(2)`
View SolutionFor examples 15, find the total energy of the block at 0.05 m from the mean position. Also,show that it issame as the P.E.
Hint `:` Total energy `=KE +PE` at maximum displacement , `KE=0` ,hence , total energy `=PE`
View SolutionAt what displacement the kinetic is equal to the potential energy ?
View SolutionFor example , at the time `t=0` , the particle is at its mean position, then at which times, the particle will have potential energy `50%` of its total energy within `t=0` to `t=T` ?
Hint `:` When PE is `50%` of total energy `(1)/( 2) kx^(2) = (1)/(2) . (1)/(2) kA^(2)`
View SolutionIs it possible for a body executing linear SHM to have a velocity of 0.03 `ms^(-1)` when its displacement is 0.04 m and a velocity of `0.04 ms^(-1)` , when its displacement is`0.03 m` ? Given amplitude and period of the oscillation are 0.05 m and 6.284 s.
Hint `: v omega sqrt(A^(2)-x^(2))`
or `v^(2) = omega^(2) ( A^(2) - x^(2))`
`0.03^(2) = omega^(2) ( A^(2) - 0.04 ^(2))` ....(1)
`0.04 ^(2) = omega^(2) ( A^(2) - 0.03^(2))` ......(2)
Solve equation (1) and(2) to find a and `omega . T = ( 2pi)/( omega)` . The values of A and T should be same as given values.
View SolutionFind the total energy of oscillations if mass of the body is 100g
A=1m , `omega`= 2
View SolutionA 10 kg collar is attached to a spring of spring constant `1000 Nm^(-1)` . It slides without friction over a horizontal surface. If is displaced from its equilibrium position by 20 cm and released . Calculate
(a) The period of oscillation (b) The maximum speed
Hint `: T= 2pi sqrt((m)/(k)) , v_(m) = A omega = A sqrt((k)/(m))`
View SolutionA 5kg collar is attached to a spring . It slides without friction over a horizontal surface. It is displaced from its equilibrium position by 10 cm and released , its maximum speed is `1 ms^(-1)` Calculate
(a) Spring constant
(b) The period of oscillation
(c ) Maximum acceleration of the collar
Hint `: m = 5 kg , A= 0.1 m ,k =?, T =? `or `a=? , v_(m) =1 ms^(-1)`
`v_(m) = Aomega =A sqrt((k)/(m))`
Find k,
` T = 2pi sqrt((m)/(k))`
` a_(max) = omega^(2) A = (k)/(m) A`
View SolutionWhat will be the time period of a pendulum which beats seconds ( i.e.,it passes through the mean position after every one second ) it its length is doubled ?
Hint `: T = 2pi sqrt((L)/(g))=2` ....(i)
`T' = 2pi sqrt((2L)/(g)) `
Fin `T'` using equation (i)
View SolutionThe acceleration due to gravity on the surface of earth is `9.8 ms^(-2)`.Time period of a simple pendulum on earth and moon are 3.5 second and 8.4 second respectively. Find the acceleration due to gravity on the moon .
Hint `: T_(e) = 2pi sqrt((L)/(g_(e))) T_(m)= 2pi sqrt((L)/(g_(m)))`
`(T_(e)^(2))/(T_(m)^(2))= (g_(m))/(g_(e))`
`g_(m) = (T_(e)^(2))/(T_(m)^(2))g_(e)`
View SolutionA simple pendulum with a metallic bob has a time period T.The bob is now immersed in a non-viscous liquid and oscillated . If the density of the liuid is `(1)/(4)` that of metal , what will be the time period of the same pendulum?
Hint `:` If the solid bob of the pendulum has relative densty D and has been submerged in a non-viscous liquid of relative density `rho` then effective acceleration due to gravity `g' = g-(g)/(n) ` where `n = (D)/( rho)`
View SolutionCalculate the time period of a simple pendulum whose length is equal to radius of earth.
Hint `: L =R_(e) = 6.4 xx 10^(6) m , g = 9.8 ms^(-2)`
`T ' = 2pi sqrt(( R_(e))/(2g))`
View SolutionIn dampled oscillation , the amplitude of oscillation is reduced to half of its initial value of 5 cm at the end of 25 osciallations. What will be its amplitude when the oscillator completes 50 oscillations ?
Hint `: A= A_(0) e^((-bt)/(2m))` , let T be the time period of oxcillation
Case -I `: (A_(0))/(2) = A_(0)e^(-bx(25T)/(2m))`
or `(1)/(2)= e^(-25(bT)/(2m))` ......(i)
Case -II` A=A_(0)e^(-bxx50(T)/(2m))`
`A _(0)(e^(-25(bT)/(2m)))^(2)`
Use euation (i) to find a .
View SolutionFor the damped oscillator shown in previous figure, `k= 180 Nm^(-1)` and the damping constant b is `40 gs^(-1)` .Period of oscillation is given as 0.3 s, find the mass of the block . (Assume b is much less than `sqrt(km))`.
Hint `: T = 2pi sqrt((m)/(k))`
View SolutionFind the time period of osciallation in the shown arrangement.

View SolutionFind time period of liquid column of length l in the shown tube.

View SolutionCategorize the motion as periodic or oscillatory motion
(i) Motion of Halley 's comet around the sun
(ii) Motion osf the penedulum of a wall clock
(iii) Motion of liquid n a U-tube when liquid is once compresed in one limb and then left to itself
Hint `:` In oscallatory motion, there is to and fro motion about some mean position.
View SolutionIs circular motion an exampleos oscillatory motion ?
Hint `:` Think - is there to and fro motion about some mean position which is the basic concept for oscillatory motion ?
View SolutionFrom the given graph , find time period and frequency for A and B.
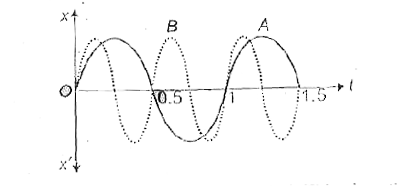
View SolutionThe beat frequency of heart of a person is 1.35 H z. How many times, does it beat in a minute ? What is the time period ?
Hint `:` Number of oscillations in `1s =1.35`
Find number of oscillations in 60 s , and `T= (1)/(v)`
View SolutionDoes `cos omegat +sin2 omega t +cos 4 omega t ` represent periodic motion ? If yes, then find the period`( omega` is any positive constant) .
Hint `:` ( Each term represents a periodic function with different angular freuency . Find the smallest interval of time after which the sum of three terms repeats ) .
View SolutionDoes `e^(omegat)` represent periodic motion ? Ifyes, then find the period `( omega ` is any positive constant )
Hint `:` (Think , Does it repeat itself)
View SolutionCategorise the following function of time ` : cos^(2) omega t` as
(a) S.H.M.
(b) Periodic but not S.H.M. Also , give the period
Hint `: cos^(2) omegat = (1)/(2) + (1)/(2) cos 2 omegat`
View SolutionCategorise the following function of time `: cos^(3) omega t ` as
(a) S.H.M.
(b) Periodic but not S.H.M. Also find the period.
Hint `:` `cos^(3) omegat= (1)/(4)( 3 cos omegat- cos 3 omegat )`
View SolutionCategorise the following function oftime `: sin omega t + cos omega t ` as
(a) Simple harmonic motion
(b) Periodic but not simple harmonic. Also, give the period.
View SolutionCategorise the following function of time `e^(omega^(2)t)` as
(a) S.H.M.
(b) Periodic but not S.H.M. Also , give period if it is periodic motion.
Hint `:` Doest it repeat itself ?
View SolutionObtain the equation of S.H.M. of a particle whose amplitude is 0.02,and whose frequency is 25 Hz. The initial phase is `(pi)/(4)`
Hint `: x= A sin ( omegat +phit)`
`omega = 2pi v`
View SolutionThe shortest distance travelled by a particle executing S.H.M. from mean position in 4 seconds is eual to `(1)/(sqrt(2))` times its amplitude. Find the time period.
Hint `: t=4 s , x = (1)/(sqrt(2)) , T=?`
`x = A sin omega t , omega = ( 2pi)/( T )`
Solve to get T.
View SolutionA harmonic osciallation is represented by `x=0.25 cos ( 6000t + 0.85)` ,where x and t are in mm and second respectively . Deduce (i) amplitude , (ii) frequency (iii) angular frequency
Hint `: ` Compare with `x= A cos ( omega t + phi)` a is amplitude frequency , `v = ( omega)/(2pi) , omega = 6000 rad s^(-1)`
View SolutionFor Question `x= A cos ( omega t + phi)` ,find (i) period and (ii) initial phase
View SolutionPlot the corresponding reference circle for given SHM `x = 2 cos ((pi)/(3) -t)` .Indicate the initial `( t- 0)` position of the particle , the radius of the circle and the angular speed of the rotating particle . Consider anticlockwise direction for rotation.
Hint `:` `x = 2 cos ((pi)/(3) -t)=2 cos ( t- (pi)/(3)) ` as ` cos ( - theta) = cos theta` . Compare with `x= A cos ( omegat + phi)`
View SolutionThe corresponding reference circle for a given SHM has been shown in the figure. Given `pi = ( 7pi)/(4)` . Write the corresponding equation of SHM. Consider anticlockwise direction for rotation.

Hint `: x= 2 cos ( 2pit+ (7pi)/( 4))`
`2 cos ((3pi)/( 2) + ( 2pit+(pi)/(4)))`
View SolutionFind the time taken by the particle in going from x = (A)/2) to `x=A` Hint :` Time taken to go from `x=0` to `x =A ` ` Time taken to go from x=0` to`x= (A)/(2)` Required time `= t_(1) - t_(2)`
View SolutionA particle startsits SHM at `t=0` . At a particular instant on its way to extreme position , `x= (A)/(2)` . Find the time taken by the particle to come back to this point after passing through the extreme position.
Hint `: t_(1) = ` time taken to go from `x=0` to `x= (A)/(2)`
`t_(2) =` time taken to go to extreme position and come back to mean position `= (T)/(2)`
Required time `= (T)/(2) - t_(1)`
View SolutionA particle executes SHM on a straight line path. The amplitude of oscialltion is 3 cm. Magnitude of its acceleration is eqal to that of its velocity when its displacement from the mean position is 1 cm. Find the time period of S.H.M.
Hint `: A= 3cm`
When`x=1 cm` , magnitude of velocity `=`magnitude of acceleration
i.e., `omega(A^(2) - x^(2))((1)/(2)) = omega^(2) x`
Find `omega`
`T = ( 2pi)(omega)`
View SolutionFor Question , find maximum velocity and maximum acceleration
Hint `:` Maximum velocity `= Aomega`
Maximum acceleration`= A omega^(2)`
A particle executes SHM on a straight line path. The amplitude of oscillation is 3cm . magnitude of its acceleration is equal to that of its velocity when its displacement from the mean position is 1cm.
View SolutionThe acceleration of a particle performing SHM is`12 cm //s^(2)` at a distance of 3 cm from the mean position . Calculate its time - period .
Hint `: a = omega^(2) x`
`a = 12 cm//s^(2) , x=3cm`
Find `omega`
`T= (pi)/(omega)`
View SolutionA particle executes simple harmonic motion about `x=0` along x-axis. The position of the particle at an instant is given by `x= ( 5 cm) sin pi t`. Find the average velocity and average acceleration for a time interval `0-0.5 s`.
Hint `:` Average velocity `=( x_(2)- x_(1))/(t_(2)-t_(1))`
`x_(1) = 5 sin 0`
`x_(2) = 5 sin ( pi xx 0.5)`
`t_(2) - t_(1) = 0.5`
Average acceleration `= ( v_(2) - v_(1))/( t_(2) - t_(1))`
`v=(dx)/(dt) = 5 pi cos pit`
`implies a _(av) = ( 5 pi cos ( pi xx 0.5) -5 pi cos theta)/(0.5)`
View SolutionIf maximum speed and acceleration of a particle executing SHM be `10 cm //s` and `100 pi cm//s^(2)` respectively ,then find its time period.
Hint `:v_("max") =A omega = 10`
`a_(max) = A omega^(2) = 100pi`
Solve to get `omega`
`T = ( 2pi)/( omega)`
View SolutionA particle of mass 2 kg is moving with SHM. Its greatest velocity is `40 ms^(-1)` and its amplitude is 20m. Find the time period and the force of attraction towards the centre when the particles is at its greates distance.
Hint `:` Maximum velocity ,`A omega = 40ms^(-1) ,A = 20 cm`, find `omega ` .
Then find `T= ( 2pi)/( omega)` Force of attractino towards centre `=` Restoring force `= m omega^(2) A`
View SolutionThe vertical motion of a huge piston in a machine is approximately SHM with a frequency of 1Hz.A block of mass 20 kg is placed on the piston . What is the maximum amplitude of the piston's SHM for the block and the piston to remain together .
Hint `:` `v= (1)/( 2pi)sqrt((k)/(m))`
Find k
For maximum displacement ` x_(max) =A`
For maximum restoring force , `F= - kA = -mg`
`:. A = (mg)/(k) = (mg) /( momega^(2))= (g)/( omega^(2))`
View SolutionThe vertical motion of a huge piston in a machine is approximately SHM. A block of 5 kg is placed on the piston. The maximum amplitude of the piston's SHM for the block and the piston to remains together is 0.99m. Find the frequency .
Hint `:` `v= (1)/( 2pi)sqrt((k)/(m))`
Find k
For maximum displacement ` x_(max) =A`
For maximum restoring force , `F= - kA = -mg`
`:. k= (mg)/( A)`. Put the valeu of K in `v =(1)/( 2pi ) sqrt((k)/(m))` to find v .
View SolutionMany builidings have other types of mass dampersas antisway devices ( Refers of Example 14) some like the Johns Honacock building in Boston,have a larger block oscillating at the end of spring and an a lubricated track. .Suppose the block has `m=5.44 xx 10^(5) kg` and is designed to oscillate at a frequency of`5 sqrt(2)` Hz and with amplitude ` x_(m) = 0.40 m` . Find the total mechanical energy E of the spring block system.
Hint `:K =m omega^(2) = m ( 2pi v ) ^(2)`
`E = K+U = (1)/(2) mv^(2) + (1)/(2) kx^(2)`
View SolutionFor Question , calculat the block's speed asit passes through the equilibrium point ?
Hint `: E = K+U = (1)/(2) mv^(2) + (1)/(2) kx^(2) = (1)/(2) mv^(2) +0` . Calculate v
View Solutionfind the potential energy of the block at 0.05 m from the mean position
View SolutionFor examples , find the potential energy of the block at 0.05 m from the mean position
View SolutionAt what displacement the kinetic is equal to the potential energy ?
Hint `: U = (1)/(2) kx^(2) , K = (1)/(2) (A^(2) - x^(2))`
`U = K`
View SolutionFor example , at the time `t=0` , the particle is at its mean position, then at which times, the particle will have potential energy `50%` of its total energy within `t=0` to `t=T` ?
Hint `:` When PE is `50%` of total energy `(1)/( 2) kx^(2) = (1)/(2) . (1)/(2) kA^(2)`
View SolutionIs it possible for a body executing linear SHM to have a velocity of 0.03 `ms^(-1)` when its displacement is 0.04 m and a velocity of `0.04 ms^(-1)` , when its displacement is`0.03 m` ? Given amplitude and period of the oscillation are 0.05 m and 6.284 s.
Hint `: v omega sqrt(A^(2)-x^(2))`
or `v^(2) = omega^(2) ( A^(2) - x^(2))`
`0.03^(2) = omega^(2) ( A^(2) - 0.04 ^(2))` ....(1)
`0.04 ^(2) = omega^(2) ( A^(2) - 0.03^(2))` ......(2)
Solve equation (1) and(2) to find a and `omega . T = ( 2pi)/( omega)` . The values of A and T should be same as given values.
View SolutionFind the total energy of oscillation if mass of the body is 100g and angular velocity 1 rad/sec and amplitude is 0.05 meter
Hint `: m = 100 xx 10^(-3) kg`
Energy `= (1)/(2) mA^(2) omega^(2)`
View SolutionA 10 kg collar is attached to a spring of spring constant `1000 Nm^(-1)` . It slides without friction over a horizontal surface. If is displaced from its equilibrium position by 20 cm and released . Calculate
(a) The period of oscillation (b) The maximum speed
Hint `: T= 2pi sqrt((m)/(k)) , v_(m) = A omega = A sqrt((k)/(m))`
View SolutionA 5kg collar is attached to a spring . It slides without friction over a horizontal surface. It is displaced from its equilibrium position by 10 cm and released , its maximum speed is `1 ms^(-1)` Calculate
(a) Spring constant
(b) The period of oscillation
(c ) Maximum acceleration of the collar
Hint `: m = 5 kg , A= 0.1 m ,k =?, T =? `or `a=? , v_(m) =1 ms^(-1)`
`v_(m) = Aomega =A sqrt((k)/(m))`
Find k,
` T = 2pi sqrt((m)/(k))`
` a_(max) = omega^(2) A = (k)/(m) A`
View SolutionWhat will be the time period of a pendulum which beats seconds ( i.e.,it passes through the mean position after every one second ) it its length is doubled ?
Hint `: T = 2pi sqrt((L)/(g))=2` ....(i)
`T' = 2pi sqrt((2L)/(g)) `
Fin `T'` using equation (i)
View SolutionThe acceleration due to gravity on the surface of earth is `9.8 ms^(-2)`.Time period of a simple pendulum on earth and moon are 3.5 second and 8.4 second respectively. Find the acceleration due to gravity on the moon .
Hint `: T_(e) = 2pi sqrt((L)/(g_(e))) T_(m)= 2pi sqrt((L)/(g_(m)))`
`(T_(e)^(2))/(T_(m)^(2))= (g_(m))/(g_(e))`
`g_(m) = (T_(e)^(2))/(T_(m)^(2))g_(e)`
View SolutionA simple pendulum with a metallic bob has a time period T.The bob is now immersed in a non-viscous liquid and oscillated . If the density of the liuid is `(1)/(4)` that of metal , what will be the time period of the same pendulum?
Hint `:` If the solid bob of the pendulum has relative densty D and has been submerged in a non-viscous liquid of relative density `rho` then effective acceleration due to gravity `g' = g-(g)/(n) ` where `n = (D)/( rho)`
View SolutionCalculate the time period of a simple pendulum whose length is equal to radius of earth.
Hint `: L =R_(e) = 6.4 xx 10^(6) m , g = 9.8 ms^(-2)`
`T ' = 2pi sqrt(( R_(e))/(2g))`
View SolutionIn dampled oscillation , the amplitude of oscillation is reduced to half of its initial value of 5 cm at the end of 25 osciallations. What will be its amplitude when the oscillator completes 50 oscillations ?
Hint `: A= A_(0) e^((-bt)/(2m))` , let T be the time period of oxcillation
Case -I `: (A_(0))/(2) = A_(0)e^(-bx(25T)/(2m))`
or `(1)/(2)= e^(-25(bT)/(2m))` ......(i)
Case -II` A=A_(0)e^(-bxx50(T)/(2m))`
`A _(0)(e^(-25(bT)/(2m)))^(2)`
Use euation (i) to find a .
View SolutionFor the damped oscillator shown in previous figure, `k= 180 Nm^(-1)` and the damping constant b is `40 gs^(-1)` .Period of oscillation is given as 0.3 s, find the mass of the block . (Assume b is much less than `sqrt(km))`.
Hint `: T = 2pi sqrt((m)/(k))`
View Solution
Try Yourself questions and complete solutions for chapter OSCILLATIONS of AAKASH INSTITUTE ENGLISH of Class 12
All Exercises from AAKASH INSTITUTE Class 12 PHYSICS OSCILLATIONS
- ASSIGNMENT ( SECTION-E(ASSERTION-REASON TYPE QUESTION) )
- ASSIGNMENT (SECTION -D( Comprehension) )
- ASSIGNMENT (SECTION-B )
- ASSIGNMENT ( SECTION -A)
- ASSIGNMENT ( SECTION-C )
- ASSIGNMENT ( SECTION-F( MATRIX MATCH TYPE QUESTIONS) )
- ASSIGNMENT ( Section-G( Integers Answer Type Question) )
- ASSIGNMENT ( SECTION-H ( MULTIPLE TRUE-FALSE TYPE QUESTIONS) )
- ASSIGNMENT ( SECTION-I(SUBJECTIVE TYPE QUESTIONS) )
- ASSIGNMENT ( SECTION-J )
- Assignment (Section - A) (OBJECTIVE TYPE QUESTIONS)
- Assignment (Section - B) (OBJECTIVE TYPE QUESTIONS)
- Assignment (Section C) (PREVIOUS YEARS QUESTIONS)
- Assignment (Section D) (ASSERTION-REASON TYPE QUESTIONS)
- EXAMPLE
- EXAMPLE 1
- Exercise
- Try Yourself