Complete Solutions to Assignment (Section - A) (OBJECTIVE TYPE QUESTIONS) of chapter OSCILLATIONS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | OSCILLATIONS |
| AAKASH INSTITUTE | Assignment (Section - A) (OBJECTIVE TYPE QUESTIONS) |
| Number Of Questions | 60 |
| Academic Year | 2023-24 |
For a particle executing simple harmonic motion, the acceleration is -
View SolutionThe phase difference between displacement and acceleration of particle in a simple harmonic motion is
View SolutionThe shape of graph plotted between velocity and position of a particle executing simple harmonic motion is
View SolutionIf particle is excuting simple harmonic motion with time period T, then the time period of its total mechanical energy is :-
View SolutionIdentify the corret definition
View SolutionThe equation of motion of a simple harmonic motion is not
View SolutionSelect wrong statement about simple harmonic motion
View SolutionThe motion of a particle executing simple harmonic motion is given by `X = 0.01 sin 100 pi (t + 0.05)`, where X is in metres andt in second. The time period is second is
View SolutionA particle moves under force `F =5(x -2)^(3)` .Motion of the particle is
View SolutionFor a particle showing motion under forces `F= - 5 ( x-2)^(2)` , the motion is
View SolutionFor a particle showing motion under forces `F= - 5 ( x-2)` , the motion is
View SolutionA boy is swinging in a swing. intially he is sitting then he stands , the time period will
View SolutionTime period of a simple pendulum in a freely falling lift will be
View SolutionIf the length of a simple pendulum is equal to the radius of the earth, its time period will be
View SolutionA particle is executing SHM with time period T. If time period of its total mechanical energy isT' then `(T')/(T) ` is
View SolutionA body executing S.H.M.along a straight line has a velocity of `3 ms^(-1)` when it is at a distance of 4m from its mean position and`4ms^(-1)` when it is at a distance of 3m from its mean position.Its angular frequency and amplitude are
View SolutionTwo identical springs have the same force constant `73.5 Nm^(-1)` . The elongation produced in each spring in three cases shown in Figure-1, Figure-2 and Figure-3 are `( g= 9.8 ms^(-2))`
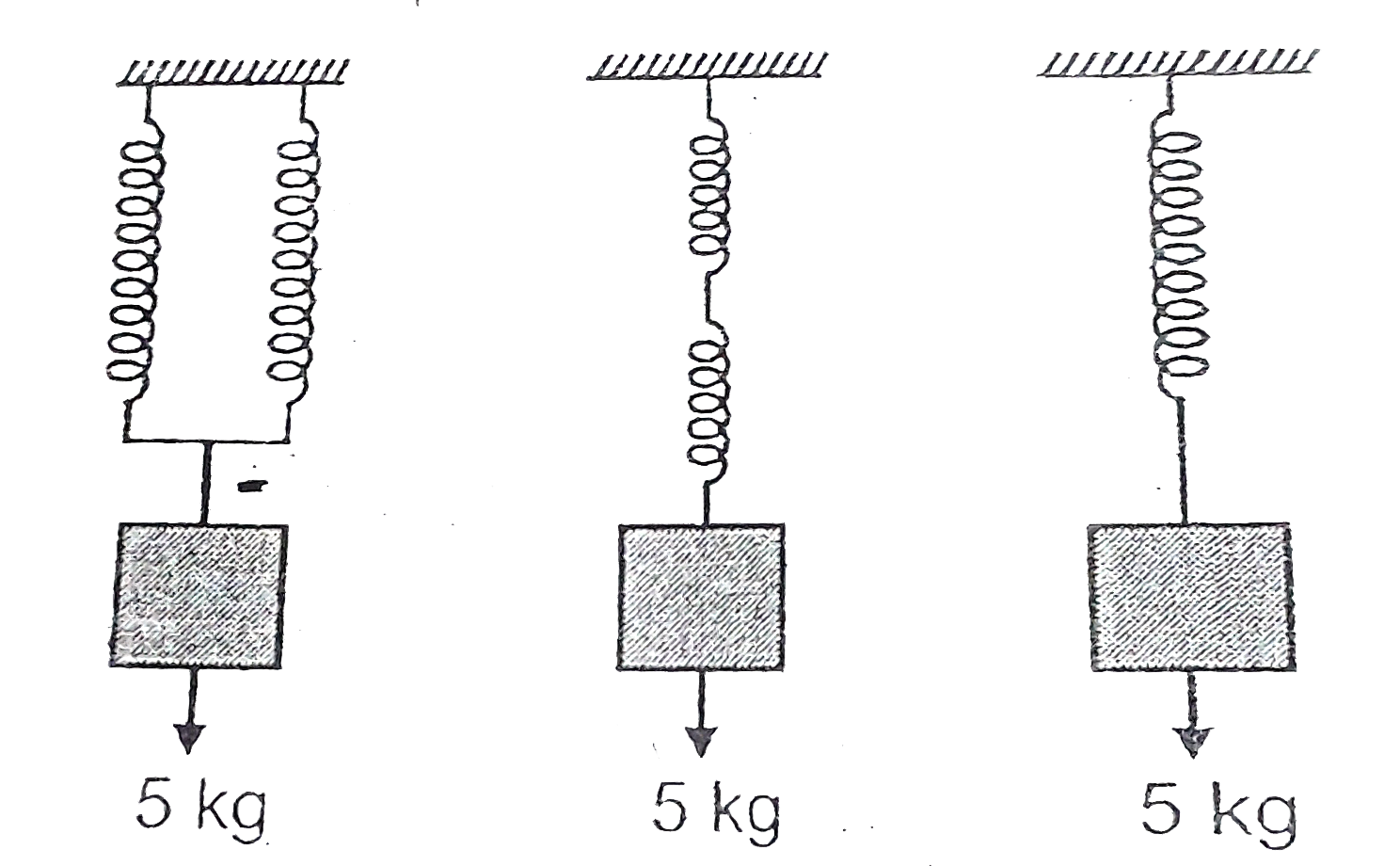
View SolutionThe frequency of oscillation of amass m suspended by a spring is `v_(1)`. If length of spring is cut to one third then the same mass oscillations with frequency `v_(2)`. Then
View SolutionTwo particles executing SHM of same frequency, meet at `x= +A//2`, while moving in opposite direction . Phase difference between the particles is
View SolutionA particle is executing SHM with time period T Starting from mean position, time taken by it to complete `(5)/(8)` oscillations is,
View SolutionA particle executes S.H.M. between `x = -A` and `x = + A`. The time taken for it to go from 0 to A/2 is `T_(1)` and to go from A/2 to A is `T_(2)`. Then
View SolutionTwo S.H.Ms are given by `y_(1) = a sin ((pi)/(2) t + (pi)/(2))` and `y_(2) = b sin ((2pi)/(3) t + (pi)/(2))` . The phase difference between these after 1 second is
View SolutionA simple harmonic motino has amplitude A and time period T. The maxmum velocity will be
View SolutionA particle is executing S.H.M. with amplitude A and has maximum velocity `v_(0)`. Its speed at displacement `(3A)/(4)` will be
View SolutionA particle executes simple harmonic motion according to equation `4(d^(2)x)/(dt^(2))+320x=0`. Its time period of oscillation is :-
View SolutionThe plot of velocity (v) versus displacement (x) of a particle executing simple harmonic motion is shown in figure. The time period of oscillation of particle is :-

View SolutionA particle of mass 10g is undergoing SHM of amplitude 10cm and period 0.1s. The maximum value of force on particle is about
View SolutionTwo identical pendulums oscillate with a constant phase difference `(pi)/(4)` and same amplitude. If the maximum velocity of one is v, the maximum velocity of the other will be.
View SolutionWhich of the following graphs best represents the variation of acceleration 'a' with displacement x?
View SolutionA body executes SHM with an amplitude a. At what displacement from the mean positions, the potentail energy of the body is one-fourth of its total energy?
View SolutionA particle of mass 4kg moves simple harmonically such that its PE (U) varies with position x, as shown. The period of oscillations is :-
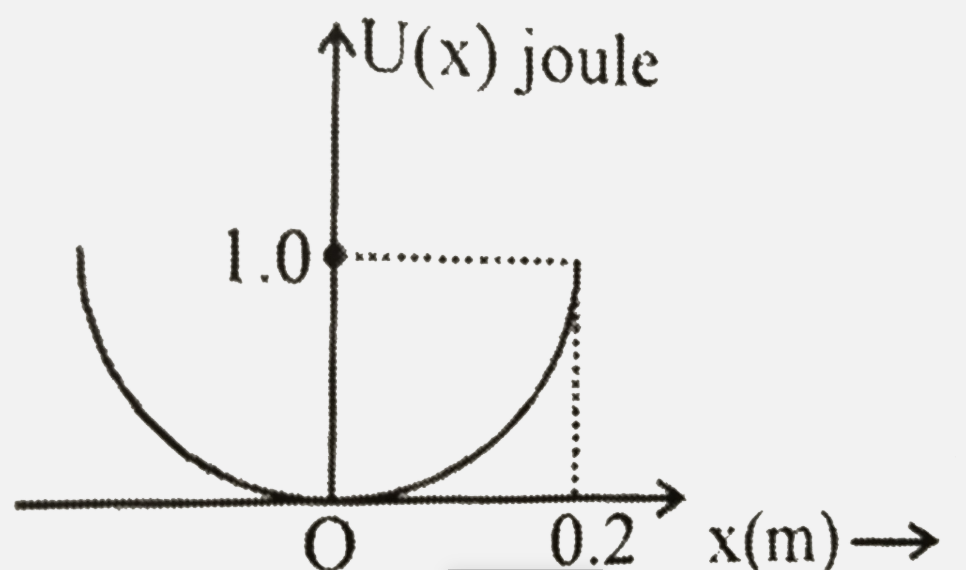
View SolutionThe kinetic energy and potential energy of a particle executing simple harmonic motion will be equal when displacement (amplitude = a) is
View SolutionA block is resting on a piston which executes simple harmonic motion in vertical plain with a period of `2.0s` in vertical plane at an amplitude just sufficient for the block to separate from the piston. The maximum velocity of the piston is
View SolutionA simple pendulum suspended from the celling of a stationary lift has period `T_(0)`. When the lift descends at steady speed, the period is `T_(1)`, and when it descends with constant downward acceleration, the period is `T_(2)` which one of the following is true?
View SolutionIf a Seconds pendulum is moved to a planet where acceleration due to gravity is 4 times, the length of the second's pendulum on the planet should be made
View SolutionA simple pendulum with a metallic bob has a time period T.The bob is now immersed in a non-viscous liquid and oscillated . If the density of the liuid is `(1)/(4)` that of metal , what will be the time period of the same pendulum?
Hint `:` If the solid bob of the pendulum has relative densty D and has been submerged in a non-viscous liquid of relative density `rho` then effective acceleration due to gravity `g' = g-(g)/(n) ` where `n = (D)/( rho)`
View SolutionTwo simple pendulum whose lengths are `100cm` and `121cm` are suspended side by side. Then bobs are pulled together and then released. After how many minimum oscillations of the longer pendulum will two be in phase again. ?
View SolutionThe time period of oscillations of a simple pendulum is 1 minute. If its length is increased b 44% then its new time period of oscillation will be
View SolutionIf the length of a clock pendulum increases by 0.2% due to atmospheric temperature rise, then the loss in time of clock per day is
View SolutionA simple pendulum is oscillating in a trolley moving on a horizontal straight road with constant acceleration a. If direction of motion of trolley is taken as positive x direction and vertical upward direction as positive y direction then the mean position of pendulum makes an angle
View SolutionThe time period of oscillation of a simple pendulum is `sqrt(2)s`. If its length is decreased to half of initial length, then its new period is
View SolutionThe graph between time period (`T`) and length (`l`) of a simple pendulum is
View SolutionA hollow sphere is filled with water. It is hung by a long thread. As the water flows out of a hole at the bottom, the period of oscillation will
View SolutionA uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is

View SolutionA uniform disc of mass m and radius r is suspended through a wire attached to its Centre. If the time period of the torsional oscillations be T, what is the torsional constant of the wire?
View SolutionA solid cylinder of denisty `rho_(0)`, cross-section area A and length `l` floats in a liquid `rho(gtrho_(0)` with its axis vertical, . If it is slightly displaced downward and released, the time period will be :
View SolutionA block of mass m hangs from three springs having same spring constant k. If the mass is slightly displaced downwards, the time period of oscillation will be

View SolutionTwo masses `m_(1) = 1kg and m_(2) = 0.5 kg` are suspended together by a massless spring of spring constant `12.5 Nm^(-1)`. When masses are in equilibrium `m_(1)` is removed without disturbing the system. New amplitude of oscillation will be
View SolutionA mass m is attached to two springs of same force constant K, as shown in following four arrangements. If `T_(1), T_(2), T_(3) and T_(4)` respectively be the time periods of oscillation in the following arrangements in which case time period is maximum ?
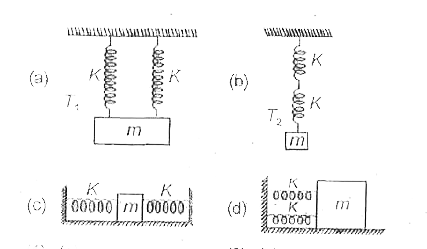
View SolutionA clock `S` is based on oscillations of a spring and clock `P` is based on pendulum motion, both clocks run at the same rate on Earth. On a planet having the same mass, but twice the radius that of the earth
View SolutionA 100 g mass stretches a particular spring by 9.8 cm, when suspended vertically from it. How large a mass must be attached to the spring if the period of vibration is to be 6.28 s?
View SolutionAn assembly of identicl spring mass system is placed on a smooth horizontal surface as shown. Initially the springs are relaxed. The left mass is displaced to the left while the right mass is displaced to the right and released. The resulting collision is elastic. The time period of the oscillatins of the system is.
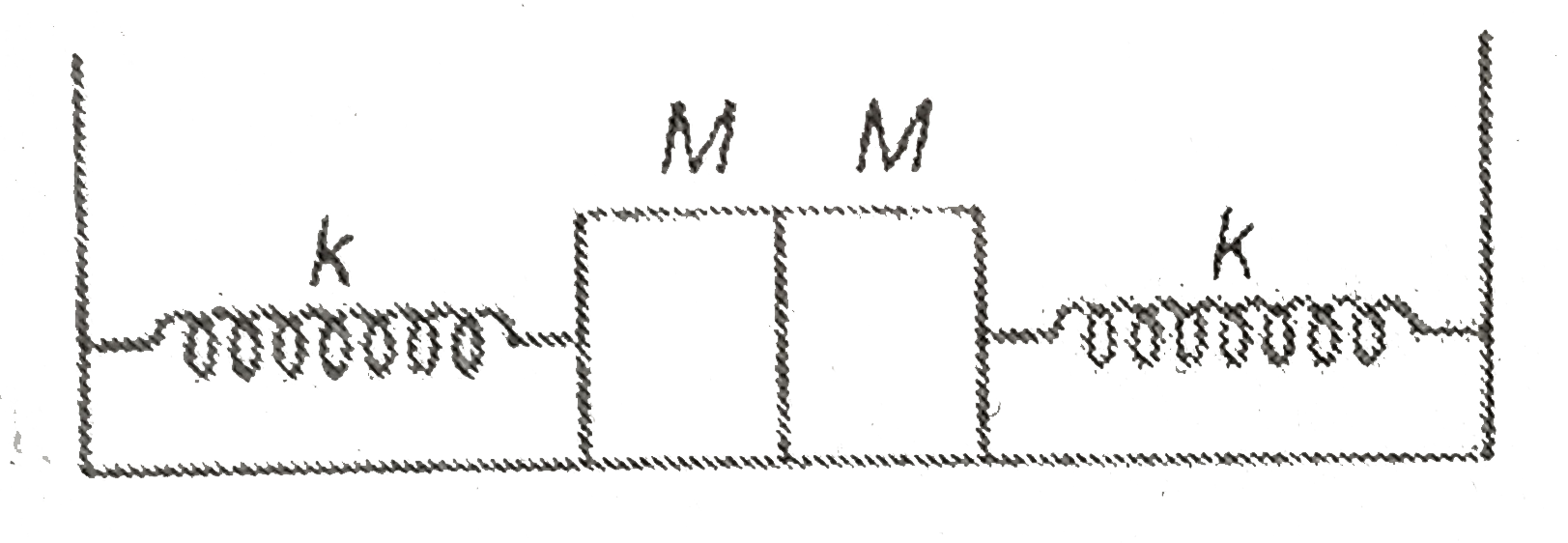
View SolutionThe time period of a mass suspended from a spring is T. If is the spring is cut into four equal parts and the same mass is suspend from one of the parts, then the new time period will be -
View SolutionLet `T_(1)` and `T_(2)` be the time periods of two springs A and B when a mass m is suspended from them separately. Now both the springs are connected in parallel and same mass m is suspended with them. Now let T be the time period in this position. Then
View SolutionIn damped oscillations damping froce is directly proportional to speed of ocillatior .If amplitude becomes half to its maximum value is 1 s, then after 2 s amplitude will be (`A_(0)`- initial amplitude)
View SolutionIn forced oscillations , a particle oscillates simple harmonically with a frequency equal to
View SolutionResonsance is a special case of
View SolutionThe SHM of a particle is given by the equation `x=2 sin omega t + 4 cos omega t`. Its amplitude of oscillation is
View SolutionA particle is acted simultaneously by matually perpendicular simple harmonic motion `x=a"cos "omegat` and `y=a "sin"omegat` . The trajectory of motion of the particle will be
View SolutionWhich of the following represents a SHM?
View Solution
Assignment (Section - A) (OBJECTIVE TYPE QUESTIONS) questions and complete solutions for chapter OSCILLATIONS of AAKASH INSTITUTE ENGLISH of Class 12
All Exercises from AAKASH INSTITUTE Class 12 PHYSICS OSCILLATIONS
- ASSIGNMENT ( SECTION-E(ASSERTION-REASON TYPE QUESTION) )
- ASSIGNMENT (SECTION -D( Comprehension) )
- ASSIGNMENT (SECTION-B )
- ASSIGNMENT ( SECTION -A)
- ASSIGNMENT ( SECTION-C )
- ASSIGNMENT ( SECTION-F( MATRIX MATCH TYPE QUESTIONS) )
- ASSIGNMENT ( Section-G( Integers Answer Type Question) )
- ASSIGNMENT ( SECTION-H ( MULTIPLE TRUE-FALSE TYPE QUESTIONS) )
- ASSIGNMENT ( SECTION-I(SUBJECTIVE TYPE QUESTIONS) )
- ASSIGNMENT ( SECTION-J )
- Assignment (Section - A) (OBJECTIVE TYPE QUESTIONS)
- Assignment (Section - B) (OBJECTIVE TYPE QUESTIONS)
- Assignment (Section C) (PREVIOUS YEARS QUESTIONS)
- Assignment (Section D) (ASSERTION-REASON TYPE QUESTIONS)
- EXAMPLE
- EXAMPLE 1
- Exercise
- Try Yourself