Complete Solutions to ASSIGNMENT ( SECTION -A) of chapter OSCILLATIONS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | OSCILLATIONS |
| AAKASH INSTITUTE | ASSIGNMENT ( SECTION -A) |
| Number Of Questions | 58 |
| Academic Year | 2023-24 |
Choose the correct statement regarding SHM
View SolutionChoose the correct statement regarding SHM
View SolutionChoose the correct statement regarding SHM
View SolutionChoose the correct statement(s) regarding SHM
View SolutionA particle moves under force `F =5(x -2)^(3)` .Motion of the particle is
View SolutionFor a particle showing motion under forces `F= - 5 ( x-2)^(2)` , the motion is
View SolutionFor a particle showing motion under forces `F= - 5 ( x-2)` , the motion is
View SolutionTime period of a spring pendulum when lift moves downward with constant velocity v is T second. When the lift moves upward with constant acceleration`= (g)/(3)` , the time period will be

View SolutionA hollow sphere is taken as bob of a simple pendulum. This hollow sphere is filled with fine sand. There is a small hole at the bottom of this sphere through which the fine sand leaks out. How does the time period of this simple pendulum alter? Discuss.
View SolutionMass suspended to a spring is pulled down by 2.5 cm and let go. The mass oscillates with an amplitude of
View SolutionA simple pendulum is taken from the equator to the pole. Its period
View SolutionThe periodic time of a simple pendulum of length 1 m and amplitude 2 cm is 5 seconds. If the amplitude is made 4 cm , its periodic time in seconds will be
View SolutionA particle shows uniform circular motion. Its motion is .
View SolutionA boy is swinging in a swing. If he stands , the time period will
View SolutionTime period of a simple pendulum in a freely falling lift will be
View SolutionEffective length of a seconds pendulum is about.
View SolutionIf the length of a simple pendulum is equal to the radius of the earth, its time period will be
View SolutionThe period of oscillation of a spring pendulum is T. If the spring is cut into four equal parts, then find the time period corresponding to each part.
View SolutionDifferent lengths of pendulum are taken from Earth's surface to `h=R` . Time period remains same for
View SolutionChoose the incorrect statement
View SolutionThe `KE` and `PE` , at is a particle executing `SHM` with amplitude `A` will be equal when its displacement is
View SolutionVariation of acceleration a of a particle executing SHM with displacement x is
View SolutionVariation of velocity v versus time t in SHM is ( Given `x =` Asinomegat)`
View SolutionIf ` y=alpha cos omega t+b sin omegat`, show that it represents SHM. Determine its amplitude.
View SolutionA particle executes SHM with frequency 4 Hz. Frequency with which its PE oscillates is
View SolutionDisplacement of a particle executing SHM s `x= 10 ( cos pi t + sin pi t)`. Its maximum speed is
View SolutionA particle oscillating under a force `vecF=-kvecx-bvecv` is a (k and b are constants)
View SolutionAmplitude of vibration is `A = (F_(0))/(p-q+r)` . Resonance will occur when
View SolutionA particle is executing SHM with time period T. If time period of its total mechanical energy isT' then `(T')/(T) ` is
View SolutionAmplitude of a particle executing SHM is a and its time period is T. Its maximum speed is
View SolutionA particle osciallates with SHM according to the equation `x= (2.5 m ) cos [ ( 2pi t ) + (pi)/(4)]` . Its speed at `t = 1.5 ` s is
View SolutionThe periodic time of a particle executing S.H.M. is12 second.After how much intervalfrom`t=0` will its displacement be half of its amplitude ?
View SolutionA body executing S.H.M.along a straight line has a velocity of `3 ms^(-1)` when it is at a distance of 4m from its mean position and`4ms^(-1)` when it is at a distance of 3m from its mean position.Its angular frequency and amplitude are
View SolutionA particle oscillates with S.H.M. according to the equation `x = 10 cos ( 2pit + (pi)/(4))`. Its acceleration at `t = 1.5 s` is
View SolutionThe time period of a particle executing S.H.M.is 12 s. The shortest distance travelledby it from mean position in 2 second is ( amplitude is a )
View SolutionTime period of a particle executing SHM is 16s.At time `t = 2s`, it crosses the mean position . Its amplitude of motion is `( 32sqrt(2))/(pi) m`. Its velocity at `t = 4s` is
View SolutionMaximum K.E. of a mass of 1 kg executing SHM is18 J . Amplitude of motion is6 cm , its angular frequency is
View SolutionA body of mass 8 kg performs S.H.M. of amplitude 60 cm. The restoring force is 120 N, when the displacement is 60 cm. The time period is
View SolutionA body of mass 8 kg performs S.H.M. of amplitude 60 cm. The restoring force is 120 N, when the displacement is 60 cm. The time period is
View SolutionA spring of force constant `600 Nm^(-1)` is mounted on a horizontal table. A mass of 1.5 kg is attached to the free end of the spring,pulled sideways to a distance of 2 cm and released . The speed of the mass when the spring is compressed by 1 cm is
View SolutionA spring of force constant `600 Nm^(-1)` is mounted on a horizontal table. A mass of 1.5 kg is attached to the free end of the spring, pulled sideways to a distance of 2 cm and released .P.E. of the mass when it momentarily comes to rest and total energy are
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant `300 Nm^(-1)` as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is

View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant `300 Nm^(-1)` as shown in the figure. If the mass is displaced from its equilibrium position by 10 cm, then maximum speed of the trolley is
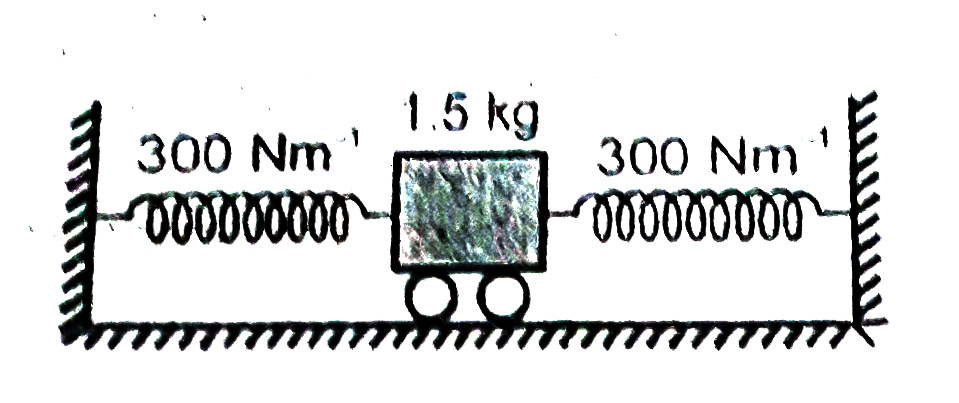
View SolutionA spring of spring constant k is cut in three equal pieces. The spring constant of each part will be
View SolutionFigure-1 to Figure -4 shows four different spring arrangements . Mass m in each arrangement is displacement from its equilibrium position and released Neglec mass of the springs. Choose the correct statement (s)

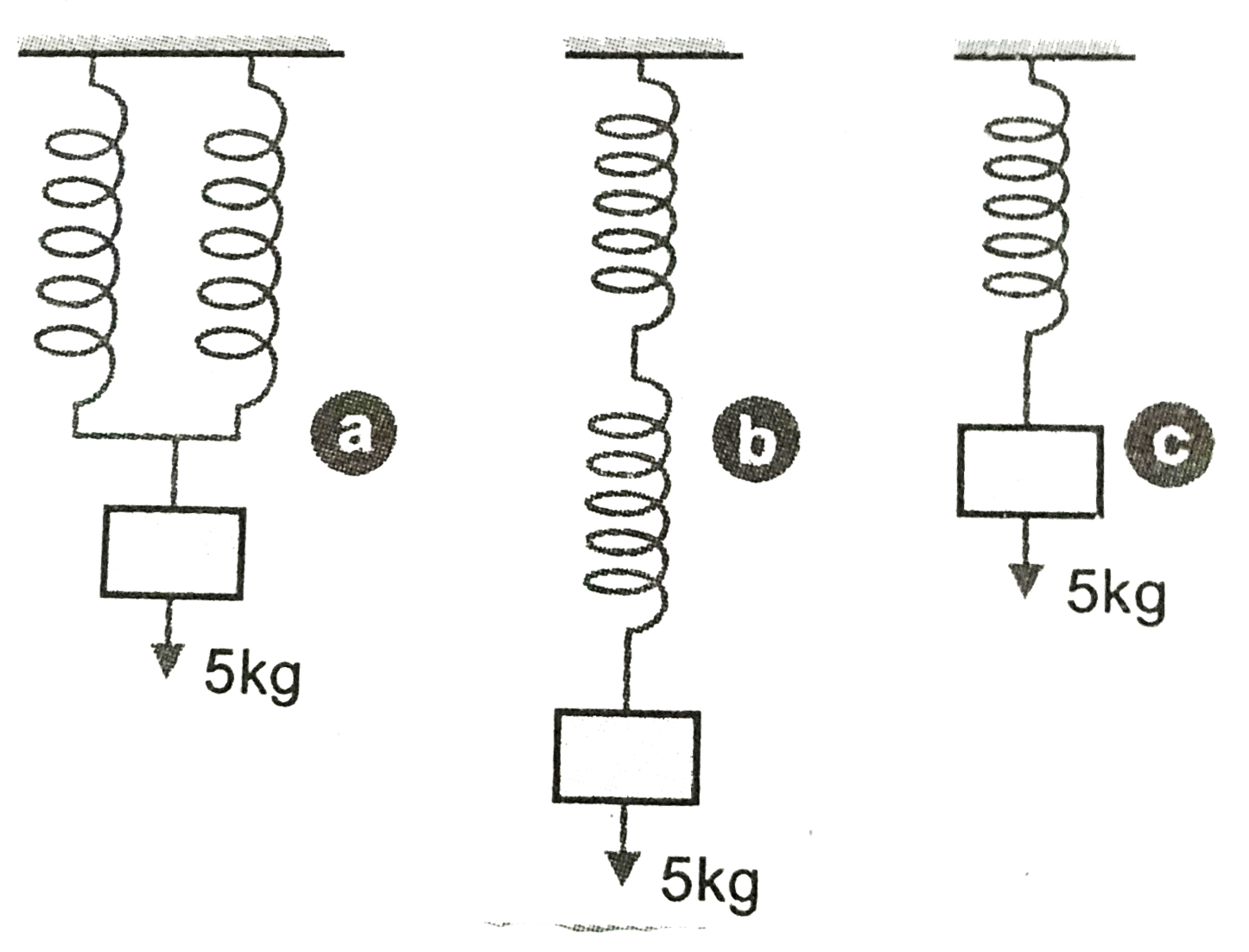
View SolutionTwo identical springs have the same force constant of `147Nm^(-1)`. What elongation will be produced in each spring in each case shown in figure? `g=9.8ms^(-2)`.
View SolutionThe frequency of oscillation of amass m suspended by a spring is `v_(1)`. If length of spring is cut to one third then the same mass oscillations with frequency `v_(2)`. Then
View SolutionThe total energy of a simple pendulum is x. When the displacement is half of amplitude,its KE will be
View SolutionThe acceleration of a body in SHM is
View SolutionIn SHM, the plot of acceleration y at time t and displacement x for one complete oscillation will be
View SolutionA uniform rod ofmass M and length L is hanging from its one end free to rotate in a veritcal plane.A small ball of equal mass is attached of the lowe end as shown. Time period of small oscillations of the rod is

View SolutionAn ideal liquid having length of liquid column l is column in V-shape take as shown. If liquid is displaced, then its time period is
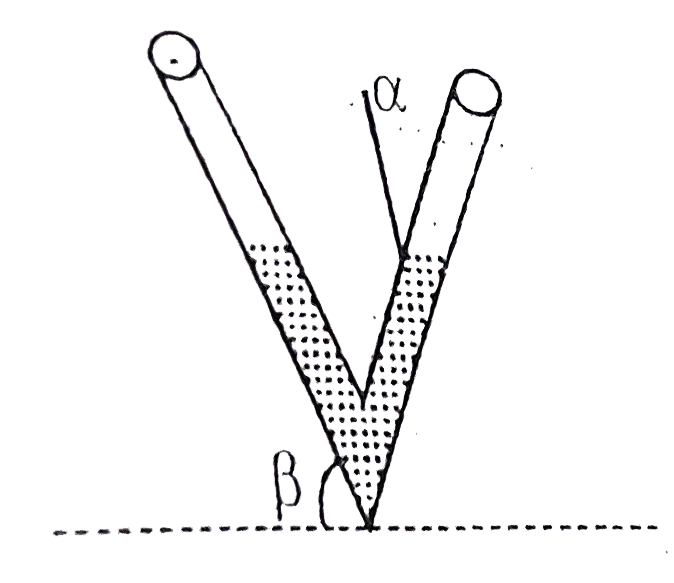
View SolutionIn the arrangement shown in figure a solid sphere is attached to spring and displaced, then it starts S.H.M. without slipping, the time period of sphere is

View SolutionA person is standing on an open car moving with a constant velocity of 30 m/s on a straight horizontal road.The men throws a ball in the vertically upward direction and it return to the person after the car has moved 240 m. The speed and angel of projection
In the previous problem if the car moving with a constant acceleration of 2 m/`s^2` , the ball will fall behind the person at a distance
A. 32m
B. 64m
C. 96m
D. 16m
View SolutionA disc is hanging from pin hole as shown in figure and displaced slightly, then its time period.

View SolutionA point mass m is supended at the end of a massless wire of length Land cross sectional are A, If Y is the Youmg's modulus of the wire. Then the frequency of the oscillation for the simple harmonic oscillation along the vertical direction is
View SolutionA heavy brass sphere is hung from a weightless inelastic string and used as a simple pendulum. Its time period of osciallation is T. When the sphere is immersed in a non-viscous liquid of density `(1)/(10)` that of brass. It acts as a simple pendulum of period.
View SolutionTwo pendulums of lengths 1.44 m and 1 m start oscillating together. After how many oscillations will Activate they again start swinging together?
View Solution
ASSIGNMENT ( SECTION -A) questions and complete solutions for chapter OSCILLATIONS of AAKASH INSTITUTE ENGLISH of Class 12
All Exercises from AAKASH INSTITUTE Class 12 PHYSICS OSCILLATIONS
- ASSIGNMENT ( SECTION-E(ASSERTION-REASON TYPE QUESTION) )
- ASSIGNMENT (SECTION -D( Comprehension) )
- ASSIGNMENT (SECTION-B )
- ASSIGNMENT ( SECTION -A)
- ASSIGNMENT ( SECTION-C )
- ASSIGNMENT ( SECTION-F( MATRIX MATCH TYPE QUESTIONS) )
- ASSIGNMENT ( Section-G( Integers Answer Type Question) )
- ASSIGNMENT ( SECTION-H ( MULTIPLE TRUE-FALSE TYPE QUESTIONS) )
- ASSIGNMENT ( SECTION-I(SUBJECTIVE TYPE QUESTIONS) )
- ASSIGNMENT ( SECTION-J )
- Assignment (Section - A) (OBJECTIVE TYPE QUESTIONS)
- Assignment (Section - B) (OBJECTIVE TYPE QUESTIONS)
- Assignment (Section C) (PREVIOUS YEARS QUESTIONS)
- Assignment (Section D) (ASSERTION-REASON TYPE QUESTIONS)
- EXAMPLE
- EXAMPLE 1
- Exercise
- Try Yourself