Complete Solutions to ASSIGNMENT (SECTION-B ) of chapter OSCILLATIONS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | OSCILLATIONS |
| AAKASH INSTITUTE | ASSIGNMENT (SECTION-B ) |
| Number Of Questions | 25 |
| Academic Year | 2023-24 |
Two particles executing SHM of same frequency, meet at `x= +A//2`, while moving in opposite direction . Phase difference between the particles is
View SolutionTwo S.H.Ms are given by `y_(1) = a sin ((pi)/(2) t + (pi)/(2))` and `y_(2) = b sin ((2pi)/(3) t + (pi)/(2))` . The phase difference between these after 1 second is
View SolutionIf a graph is plotted between velocity (v) and displacement (y) of a particle executing SHM from mean position, then the nature of the graph is
View SolutionA particle moves according to the equation `x= a cos pi t`. The distance covered by it in `2.5` s is
View SolutionTwo simple harmonic motions are given by `y _(1) = 5 sin ( omegat- pi //3). y_(2) = 5 ( sin omegat+ sqrt(3) cos omegat)`. Ratio of their amplitudes is
View SolutionIf a bob of mass 'm' is attached as shown in figure. When displaced , the pendulum will undero S.H.M. with a period T is equal to

View SolutionA particle of mass 4 kg moves along x axis, potential energy ( U ) varies with respect to x as `U = 20 + ( x-4)^(2)` , maximum speed of paritcle is at
View SolutionA block of mass m kg hanging from a verticla spring executes simple harmonic motion of amplitude 4 cm . If maximum speed of particle is `8 m//s` . Maximum acceleration of block is
View SolutionA small block of mass 2 kg is placed on a bigger block of mass 4 kg which is attached to horizontal spring of spring constant `K = 500 N //m` as shown in figure, coefficient of friction between block is 0.2 .Maximum amplitude of system so that there is no relative slipping between blocks.
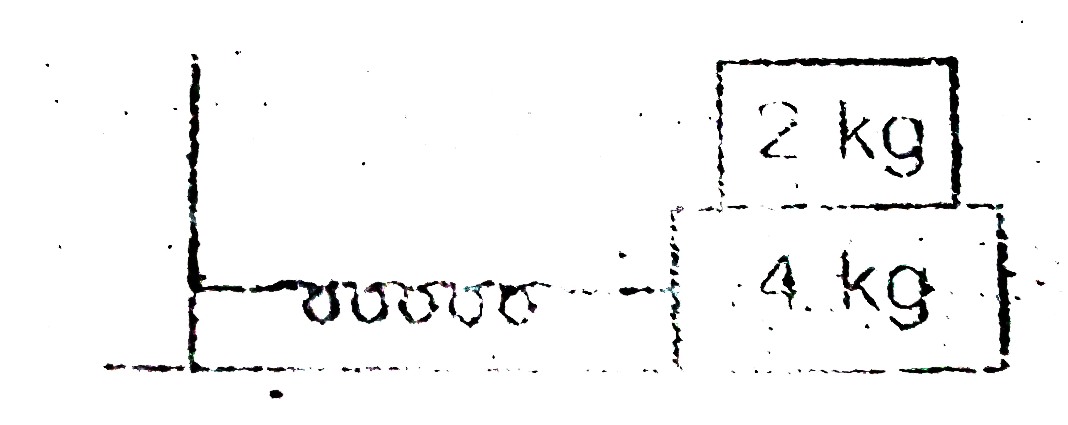
View SolutionA simple harmonic motino has amplitude A and time period T. The maxmum velocity will be
View SolutionIf a ball is dropped from height 2 metre on a smooth eleastic floor, then the time period of oscillation is
View SolutionA particle moves in a circular path with a uniform speed. Its motion is
View SolutionThe average acceleration in one time period in a simple harmonic motion is
View SolutionA block of mass 1 kg is placed inside a car of mass 5 kg , as shown . The block can slide smoothly along horizontal direction. If block is displaced slightly and released , then time period of osciallation is

View SolutionA car is moving on a horizontal road with constant acceleration 'a' . A bob of mass 'm' is suspended from the ceiling of car. The mean position about which the bob will oscillate is given by `( 'theta'` is angle with vertical)
View SolutionIf a particle is executing S.H.M. then the graph between its acceleration and velocity is , in general
View SolutionA particle moves along x-axis according to relation `x= 1+2 sin omegat`. The amplitude of S.H.M. is
View SolutionIn a S.H.M. with amplitude 'A', what is the ratio of K.E. and P.E. at `(A)/(2)` distance from the mean position ?
View SolutionWhatis the displacement equation of S.H.M. with an amplitude 2m , if 120 oscillations are performed during one minute and initial phase is `60^(@)` [ Consider displacement time equation of the form `y = A sin( omega t + phi)]` ?
View SolutionA simple pendulum of mass 'm' , swings with maximum angular displacement of `60^(@)` . When its angular displacement is `30^(@)` ,the tension in the string is
View SolutionIf P.E. of a system is given by relation `U= (A)/(x^(2))-(B)/(x)`, where 'A'and'B' are positive constant, then the mean positive of S.H.M.is
View SolutionIf displacement time equation of an S.H.M. is`x= sin . (pit)/(6)` , then the moment of times at which peak value of acceleration is attained are
View SolutionIf a particle executres S.H.M. with time period 4 s when magnitude of resotring force constant is5 `N//m` and with timper period2 s when magnitude restoring force constant is ` 20 N //m`, then time period under the combined action of two forces willl be
View SolutionA pendulum has a period `T` for small oscillations. An obstacle is placed directly beneath the pivot, so that only the lowest one - quarter of the string can follow the pendulum bob when it swings to the left of its resting position. The pendulum is released from rest at a certain point. How long will it take to return to that point again ? In answering this question, you may assume that the angle between the moving string and the vertical stays small throughout the motion.

View SolutionOne end of a long metallic wire of length L is tied to the ceiling. The other end is tied to massless spring of spring constant k. A mass m hangs freely from the free end of the spring . The area of cross-section and Young's modulus of the wire are A and Y respectively . If the mass is slighty pulled down and released , it will oscillate with a time period T equal to
View Solution
ASSIGNMENT (SECTION-B ) questions and complete solutions for chapter OSCILLATIONS of AAKASH INSTITUTE ENGLISH of Class 12
All Exercises from AAKASH INSTITUTE Class 12 PHYSICS OSCILLATIONS
- ASSIGNMENT ( SECTION-E(ASSERTION-REASON TYPE QUESTION) )
- ASSIGNMENT (SECTION -D( Comprehension) )
- ASSIGNMENT (SECTION-B )
- ASSIGNMENT ( SECTION -A)
- ASSIGNMENT ( SECTION-C )
- ASSIGNMENT ( SECTION-F( MATRIX MATCH TYPE QUESTIONS) )
- ASSIGNMENT ( Section-G( Integers Answer Type Question) )
- ASSIGNMENT ( SECTION-H ( MULTIPLE TRUE-FALSE TYPE QUESTIONS) )
- ASSIGNMENT ( SECTION-I(SUBJECTIVE TYPE QUESTIONS) )
- ASSIGNMENT ( SECTION-J )
- Assignment (Section - A) (OBJECTIVE TYPE QUESTIONS)
- Assignment (Section - B) (OBJECTIVE TYPE QUESTIONS)
- Assignment (Section C) (PREVIOUS YEARS QUESTIONS)
- Assignment (Section D) (ASSERTION-REASON TYPE QUESTIONS)
- EXAMPLE
- EXAMPLE 1
- Exercise
- Try Yourself