Complete Solutions to ASSIGNMENT ( SECTION-J ) of chapter OSCILLATIONS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | OSCILLATIONS |
| AAKASH INSTITUTE | ASSIGNMENT ( SECTION-J ) |
| Number Of Questions | 8 |
| Academic Year | 2023-24 |
As a result of adding two mutually perpendicular oscillations of equal frequency the motion of an object occurs alongan ellipse, in one case the motion is clockwise, while in the other it is counter clockwise . Write the equations of motion along each coordinate axis, assuming that the initial phase along the x-axis is zero.
View SolutionA ball of mass, m is attractive to two springwhich are already stretched so that each pulls on to ball with a force F. length of each spring . In this Determine the period of small oscillations of the ball in a difference perpendicular of length of psirng. Difference of the mass of spring and gravity .

View SolutionA solid cylinder of mass m length L and radius R is suspended by means of two ropes of length l each as shown. Find the time period of small angular oscillations of the cylinder about its axis AA'
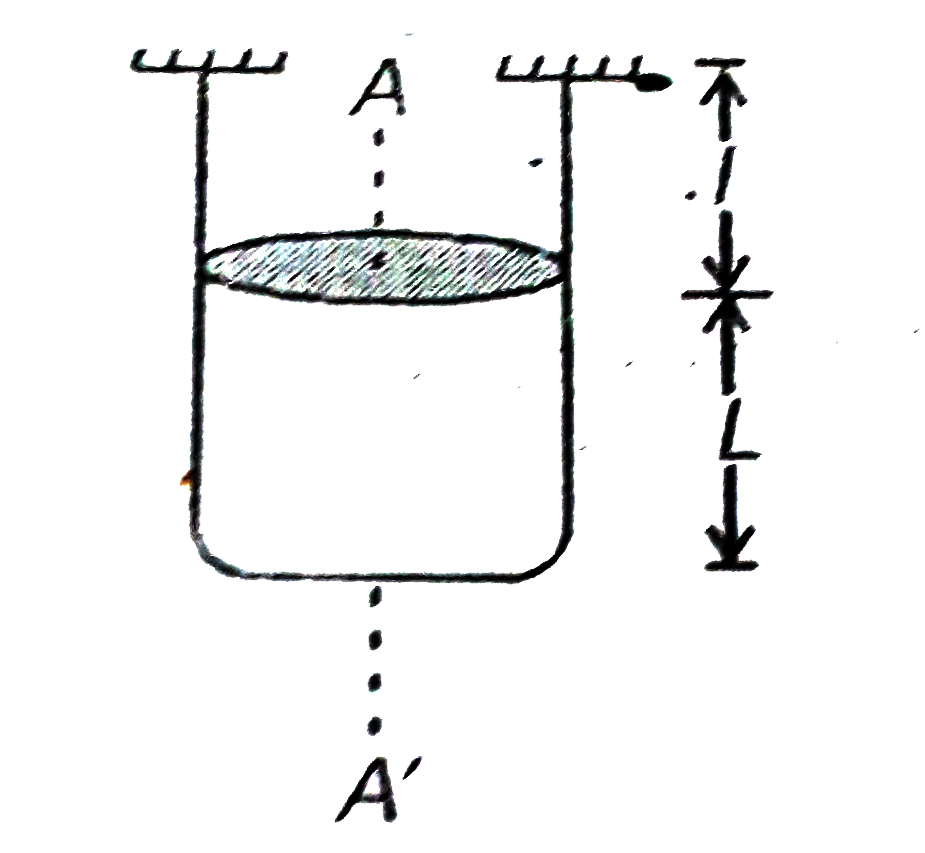
View SolutionA particle of mass 3 kg moves in aone dimensional field along x-axis. The force due to the field depends on its position as `F= 729 x^(6) - 64` . Find the state equilibrium position. Determine the time period of osciallations for small amplitude osciallations about the stable equlibrium position.
View SolutionThe block of M in the figure is connected to a left spring `(k_(1)= k)`. The right spring `(k_(2) = 2k)` is fixed to the other wall such that its free end is 6 cm away from blocm. In this situation, entire system isin equilibrium. Now, block is displaced to left by `6 sqrt(2)` cm and released. Determine the time period of oscillatory motion of the block.
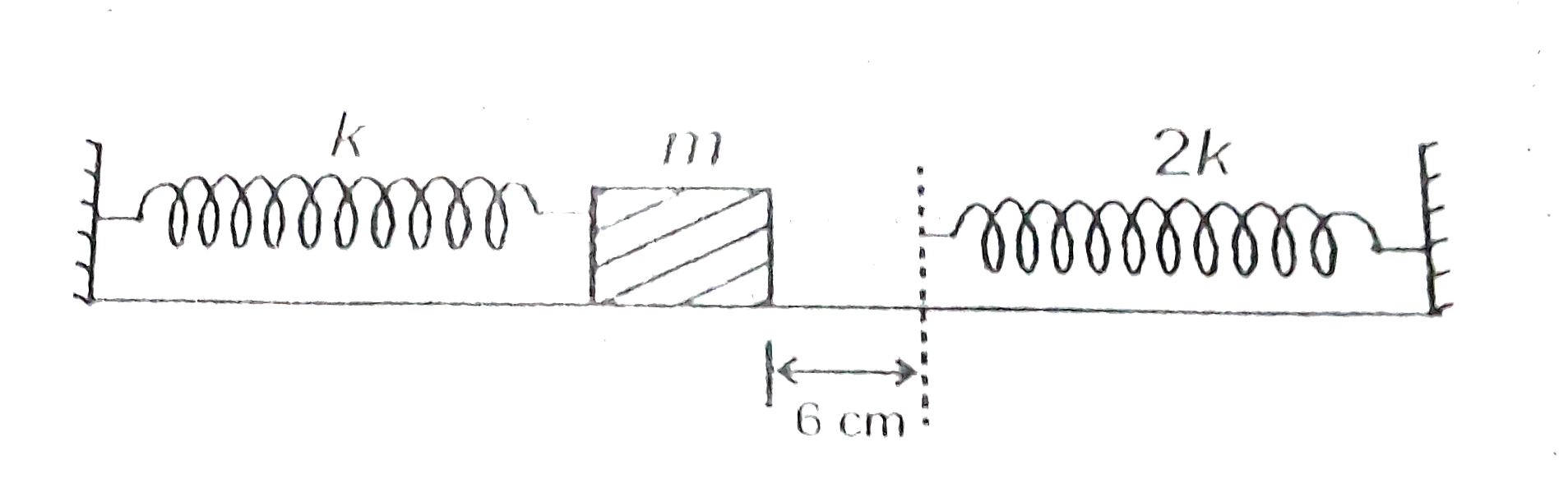
View SolutionFor a diatomic gas having 3 translational and 2 rotational degree of freedom ,the energy is given by ?
View SolutionA particle of mass `m` is allowed to oscillate near the minimum of a vertical parabolic path having the equaiton `x^(2) =4ay`. The angular frequency of small oscillation is given by
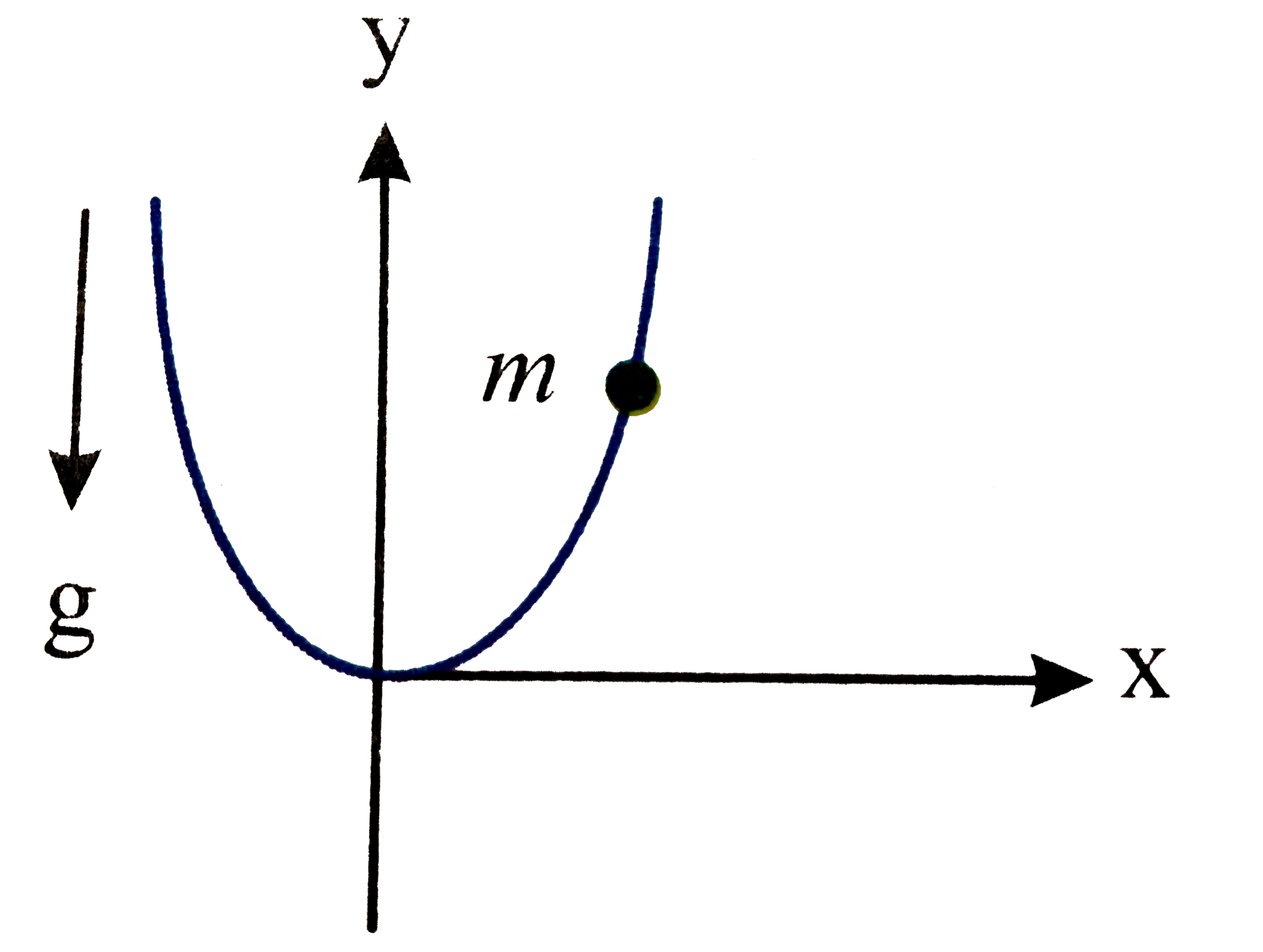
View SolutionFind the angular frequency of motion of disc of mass m and radius r for small motion (Assuming that disc rolls without slipping ) of disc.When we neglect the inertial effect of rod BD, spring constant are `k_(1)` and `k_(2)` as shown in figure.
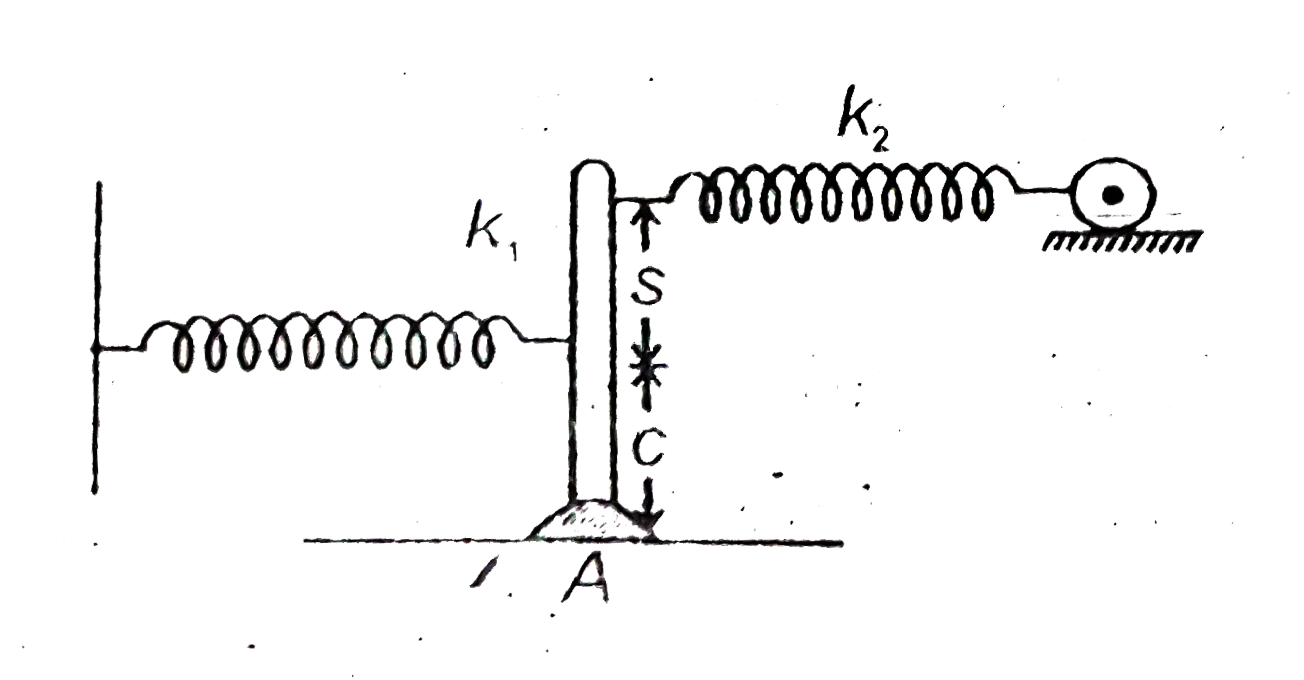
View Solution
ASSIGNMENT ( SECTION-J ) questions and complete solutions for chapter OSCILLATIONS of AAKASH INSTITUTE ENGLISH of Class 12
All Exercises from AAKASH INSTITUTE Class 12 PHYSICS OSCILLATIONS
- ASSIGNMENT ( SECTION-E(ASSERTION-REASON TYPE QUESTION) )
- ASSIGNMENT (SECTION -D( Comprehension) )
- ASSIGNMENT (SECTION-B )
- ASSIGNMENT ( SECTION -A)
- ASSIGNMENT ( SECTION-C )
- ASSIGNMENT ( SECTION-F( MATRIX MATCH TYPE QUESTIONS) )
- ASSIGNMENT ( Section-G( Integers Answer Type Question) )
- ASSIGNMENT ( SECTION-H ( MULTIPLE TRUE-FALSE TYPE QUESTIONS) )
- ASSIGNMENT ( SECTION-I(SUBJECTIVE TYPE QUESTIONS) )
- ASSIGNMENT ( SECTION-J )
- Assignment (Section - A) (OBJECTIVE TYPE QUESTIONS)
- Assignment (Section - B) (OBJECTIVE TYPE QUESTIONS)
- Assignment (Section C) (PREVIOUS YEARS QUESTIONS)
- Assignment (Section D) (ASSERTION-REASON TYPE QUESTIONS)
- EXAMPLE
- EXAMPLE 1
- Exercise
- Try Yourself