Complete Solutions to NUMERICAL EXAMPLES of chapter REFRACTION OF LIGHT of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | REFRACTION OF LIGHT |
| CHHAYA PRAKASHINI | NUMERICAL EXAMPLES |
| Number Of Questions | 75 |
| Academic Year | 2023-24 |
A ray of light is incident from water on the surface of separation of air and water at an angle `30^(@)`, Calculate the angle of refraction in air. `mu` of water `=(4)/(3)`
View SolutionA ray of light is incident on a block of glass in such a way that the angle between the reflected ray and the refracted ray is `90^(@)` . Determine the relation between the angle of incident and the refraction index of glass.
View SolutionRefractive index of glass is 1.5 and refractive index of water is 1.33. If the velocity in glass is `2 xx 10^(8) m * s^(-1)`, is the velocity of light in water?
View SolutionA monochromatic ray of light is refracted from vacuum to a medium of refractive index `mu`. Determine the relation of the wavelengths of light in vacuum and in medium.
View SolutionIf a ray of light is incident on a plate inside water at an angle of `45^(@)`, what is the angle of refraction inside the plate? Given that the absolute refractive indices of the plate and water are 1.88 and 1.33 respectively.
View SolutionHow much time will sunlight take to pass through the glass window of thickness 4 mm ? `mu` of glass = 1.5.
View SolutionGreen light of wavelength 5640 in incident on an airglass interface. If the refractive index of glass is 1.5 what will be the wavelength of light in glass?
View SolutionA ray of light is incident on the plane face of a liquid at an angle `45^(@)` and due to refraction the ray is deviated through an angle `15^(@)`. Calculate the refractive index of the liquid.
View SolutionThe opposite faces of a glass slab of thickness 15 cm are parallel. If a ray of light is incident on the glass slab at an angle `60^(@)`, calculate the lateral displacement of the ray when it emerges from the slab. `[mu " "" of glass" = 1.5]`
View SolutionA ray of light is refracted through a transparent sphere of refractive from `mu` in such a way that the ray passes through the ends of two radii inclined at an angle `theta` with each other. If `delta` is the angle of deviation of the ray while passing through the sphere then prove that,
`mu=("cos"(1)/(2)(theta-delta))/("cos"(theta)/(2))`
View SolutionA parallel beam of rays of width 20 cm passing through a glass slab makes an angle `phi=60^(@)` with its plane surface. If the beam emerges into air from this surface then calculate the width of emergent beam. Refractive index of glass = 1.8.
View SolutionRefractive index of water with respect to air is 1.33, refractive index of oil with respect to water is 1.45 and that of glass with respect to oil is 0.78. What is the refractive index of glass with respect to air?
View SolutionThere is a mark at the bottom of a beaker. A liquid of refractive index 1.4 is poured into it. If the depth of the liquid is 3.5 cm then determine how much will the mark appear to rise when it is viewed from above?
View SolutionThere is a black spot at the bottom of a rectangular glass slab of thickness d and refractive index `mu`. When the spot is viewed perpendicularly from above, the spot appears to be shifted through a distance `(mu-1)/(mu)` towards the observer. Prove it.
View SolutionIn a beaker partly filled with water, the depth of water seems to be 9cm. On pouring more water in it, the real depth of water is increased by 4cm. Now the apparent depth of water seems to be 12 cm. Determine the refractive index of water and initial depth of water in the beaker.
View SolutionA small air bubble exists inside a transparent cube of side 15 cm each. The apparent of the bubble observed from one face is 6 cm and from the opposite face its apparent distance becomes 4 cm. Determine the real distance of the bubble from the first face and refractive index of the material of the cube.
View SolutionA vessel is filled with two mutually immiscible liquids of refractive indices `mu^(1) and mu^(2)`. The depths of the two liquids are `d_(1) and d_(2)` respectively. There is a mark at the bottom of the vessel. Show that the apparent depth of the mark when viewed normally is given by `((d_(1))/(mu_(1))+(d_(2))/(mu_(2))).`
View SolutionA rectangular slab of refractive index `mu` is placed on another slab of refractive index 3. Both the slabs are of the same dimensions. There is a coin at the bottom of the lower slab. What should be the value of `mu` such that when viewed normally from above, the coin appears to be at the surface of separation of the two slabs?
View SolutionA tank contains ethyl alcohol of refraction index 1.35. The depth of alcohol is 308 cm. A plane mirror is placed horizontally at a depth of 154 cm in it. An object is placed 254 mm above the mirror. Calculate the apparent depth of the image formed by the mirror.
View SolutionA 20 mm thick layer of water `(mu=(4)/(3))` floats on a 35 mm thick layer of another liquid `(mu=(7)/(5))` in a tank. A small coin lies at the bottom of the tank. Determine the apparent depth of the coin when viewed normally from above the water.
View SolutionIf a point source is placed at a distance of 18 cm from the pole of a concave mirror, its image is formed at a distance of 9 cm from the mirror. A glass slab of thickness 6 cm is placed between the point source and the mirror such that the parallel faces of the glass slab remains perpendicular to the principal axis of the mirror. If the refractive index of glass is 1.5 what will be the displacement of the image?
View SolutionA plane mirror is made of glass having thickness 1.5 cm. its back surface is coated with mercury. A man is standing at a distance of 50 cm from the front face of the mirror. If he looks at the mirror normally, where can he find his image behind the front face of the mirror? Refractive index of glass = 1.5.
View SolutionAn observer can see the topmost point of a narrow rod of height h through a small hole [Fig.2.24]. The rod is placed inside a beaker. The beaker's height is 3h and radius is h. When the beaker is filled up to 2h of its height with a liquid the observer can see the entire rod. What is the value of the refractive index of the liquid?
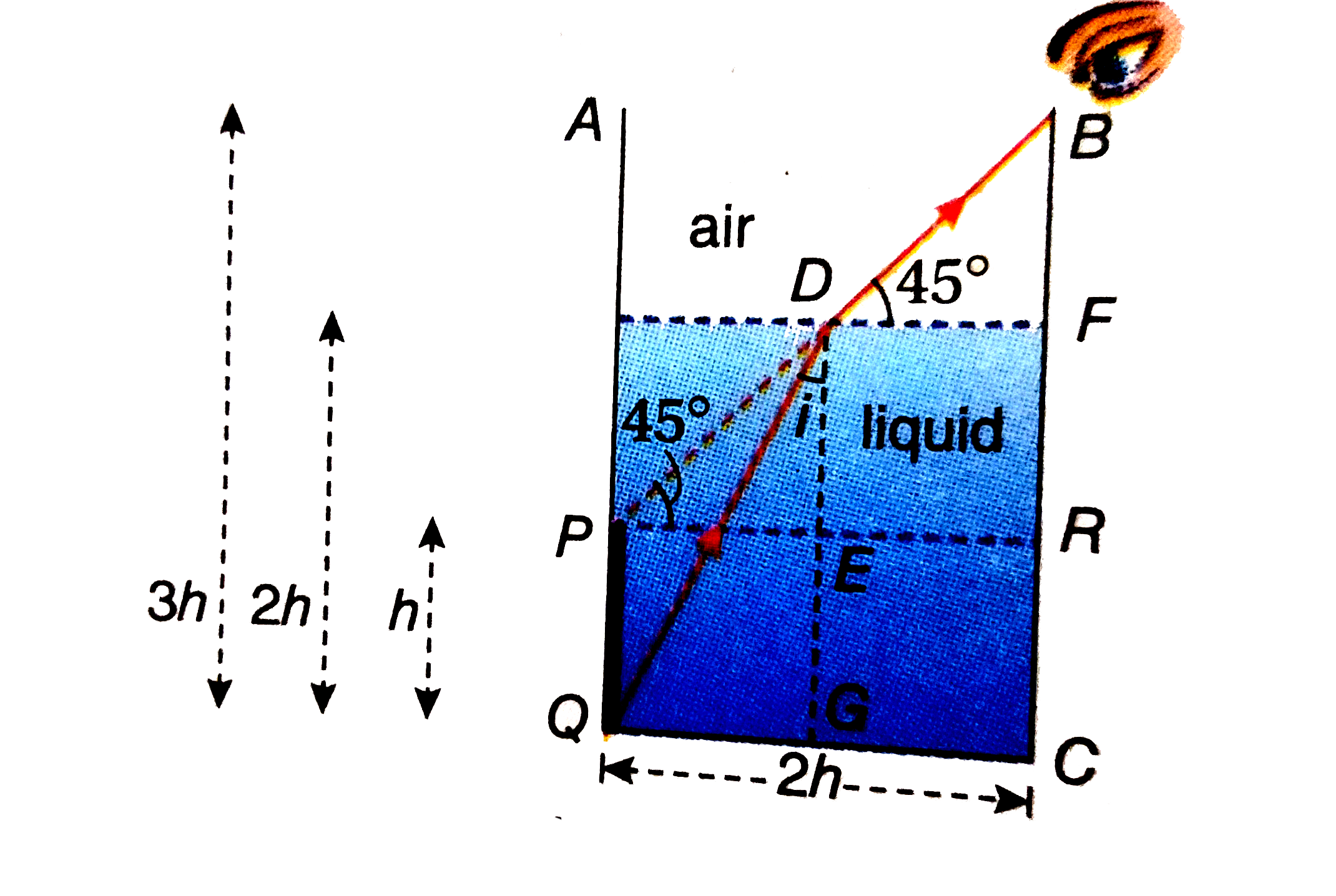
View SolutionA ray of light is incident at the interface of glass and water at an angle of incidence i. If the ray finaily emerges parallel to the surface of water as shown in the Fig. 226, then what will be the value of `mu_(g)` ?

View SolutionIf the absolute refractive index of a medium is `sqrt2`, calculate the critical angle of glass to the medium. Given that the critical angle of glass to air is `30^(@)`.
View SolutionRefractive index of carbon disulphide for red light is 1.634 and the difference in the values of critical angle for red and blue light at the surface of separation of carbon disulphide and air is `0^(@)56'`. What is the value of refractive index of carbon disuphide for blue light?
View SolutionIf the refractive index of diamond is 2.42, prove that all the beam of rays having angle of incidence more than `25^(@)` will be totally reflected. `[sin24.41^(@)` = 0.4132]
View SolutionA ray of light will go from diamond to glass. What should be the minimum angle of incidences at the surface of separation of the two media, diamond and glass, so that the ray of light cannot be refracted in glass ? `mu` of glass = 1.51 and `mu` of diamond = 2.47, `sin37.69^(@) = 0.61134`
View SolutionA cube has refractive index `mu_(1)` . There is a plane of refractive index `mu_(2)(mu_(2) lt mu_(1))` upon it. A ray travelling through air is incident on a side face of the cube. The refracted ray is incident on the upper face of the cube at the minimum angle for total internal reflection to occur. Finaily the reflected ray emerges from opposite face. Show that if the angle of emergence is `phi` then `sin phi = sqrt(mu_(1)^(2) - mu_(2)^(2)).`
View SolutionA ray of light travelling through a denser medium is incident at an angle I in a rarer medium. If the angle between the reflected ray and refracted ray is `90^(@)` , show that the critical angle of the two media, `theta_(c) = sin^(-1) (tan i)`
View SolutionA nail is fixed up perpendicularly at the centre of a circular wooden plate. Keeping the nail at bottom, the circular plate is made of float in water. What should be the maximum ratio of the radius of the plate and length of the nail so that the nail wil be out of vision? Refractive index of water = `(4)/(3)`.
View SolutionThe critical angle of glass relative to a liquid is `57^(@)20'`. Calculate the velocity of light in the liquid. Given `mu` of glass = 1.58, Velocity of light in vacuum `3 ×10^(8) m * s^(-1) and sin 57^(@)20' = 0.8418`.
View SolutionA transparent solid cylindrical rod has a refractive index of `(2)/(sqrt3).` It is surrounded by air. A light ray is incident at the midpoint of one end of the rod as shown in Fig 2.31. Determine the incident angle `theta` for which the light ray grazes along the wall of the rod.

View SolutionA point source of light is placed at a depth of h below the calm surface of water. From the source, light rays can only be transmitted to air through a definite circular section. (i) Draw the circular section of the surface of water by ray diagram and mark its radius r. (ii) Determine the angle of incidence of a ray of light incident at any point on the circumference of the circular plane. `["Given : refractive index of water", mu = (4)/(3) , 48^(@)36' = sin^(-1)]` (iii) Show that `r = (3)/(sqrt7)h.`
View SolutionThe water in a pond has a refractive index `(5)/(3)`. A source of light is placed 4 m below the surface of water. Calculate the minimum radius of an opaque disc needed to be floated on water so that light does not come out.
View SolutionFig.2.41 shows a longitudinal cross section of an optical fibre made of glass of refractive index 1.68. The pipe is coated with a material of refractive index 1.44. pipe is coated with a material of refractive index 1.44. What is the range of the angles of the incident rays with the axis of the pipe for which total reflection inside the fibre can take place?

View SolutionIn which direction will the sun appear to set if the observe is inside the water of a pond? Refractive index of water , `mu = 1.33.`
View SolutionThe refractive index of the material of a prism is `sqrt((3)/(2)` and the refractive angle is `90^(@)` . What are the values of the angle of minimum deviation of the prism and the angle of the incidence at the minimum deviation position?
View SolutionThe refractive index of the material of a prism is `sqrt(2)` and the angle of minimum deviation is `30^(@)` . Calculate the value of the refracting angle of the prism.
View SolutionThe angle of minimum deviation is the same as the angle of a glass prism of refractive index `mu = sqrt3.` What is the angle of the prism?
View SolutionWhat will be the angle of emergence of a ray of light through a prism for an angle of incidents `45^(@)` ? The angle of the prism = `60^(@)` , refractive index of the prism =`sqrt2`.
View SolutionA ray of light is incident at an angle of incidents `40^(@)` on a prism having refractive index 1.6 . What should be the value of the angle of the prism for minimum deviation?
Given `sin 40^(@) = 0.6428 , sin 23^(@)42'=0.4018.`
View SolutionThe refracting angle of a glass prism is `60^(@)` and the refractive index of glass is 1.6. If the angle of incidence of a ray of light on the first refracting surface is `45^(@)` Calculate the angle of deviation of the ray . Given that `sin 26^(@)14' = 0.4419, " " sin33^(@)46' = 0.5558 and sin62^(@)47' = 0.8893`
View SolutionIf the refracting angle of a prism is A, the refractive index of its material is `mu` and the angle of deviation of a ray of light incident normally on the first refraction face is `delta`, then prove that `mu = sin(A + delta)/(sinA).`
View SolutionA ray of light is incident at an angle of `60^(@)` on a face of a prism with refracting angle `30^(@)` . If the ray emerges from the other face and makes an angle of `30^(@)` with the incident ray then, show that the emergent ray passes perpendicularly through the refracting surface. Determine the refractive index of the material of the prism.
View SolutionA glass prism of refracting angle `60^(@)` and of refractive index 1.6, is immersed in water (refractive index is 1.33). What is its angle of minimum deviation ? `[sin 36.87^(@) = 0.6]`
View SolutionA ray of light passes through an equilateral prism in such a way that the angle of incidence becomes equal to the angle of emergence and each of these angles are `(3)/(4)`th of the angle of deviation. Determine the angle of deviation.
View SolutionThe angle of minimum deviation of a glass prism refraction angle `60^(@)` is `30^(@)` . If velocity of light in vacuum is `3 xx 10^(8) m * s^(-1)`, then determine its velocity glass.
View SolutionA very thin prism deviates a ray of light through `5^(@)` . If the refractive index of the material of the prism is 1.5 , what is the value of the angle of prism?
View SolutionA prism having refracting angle `4^(@)` is placed in air Calculate the angle of deviation of a ray incident normally or nearly normally on it. The refractive index of the material of the prism `=(3)/(2)` .
View SolutionA thin prism with refracting angle `5^(@)` and having refracting index 1.6 is kept adjacent to another thin prism having refractive index. 1.5 such that one is inverted with respect to the other. An incident ray falling vertically on the first prism passes through the second prism without any deviation. Calculate the refracting angle of the second prism.
View SolutionTo get emergent ray from a right-angled prism its refractive index should not exceed `sqrt2` - prove it.
View SolutionThe refractive index of a prism having refracting angle `75^(@)` is `sqrt2` . What should be the minimum angle of incidence on a refracting surface so that the ray will emerge from the other refracting surface of the prism?
View SolutionFind the value of the limiting angle of incidence if the refractive index of the material of prism is 1.333 and angle of prism is `60^(@)` .
View SolutionThe refracting angle of a prism is `60^(@)` and its refractive index is `sqrt((7)/(3)`. What should be the minimum angle of incidence on the first refracting surface so that the ray can emerge somehow from the second refracting surface?
View SolutionThe refractive index of the material of a prism is `sqrt((3)/(2)` and the refractive angle is `90^(@)` . Calculate the angle of minimum deviation and the corresponding angle of incidence. Show that the limiting angle of incident for getting emergent ray is `45^(@)`.
View SolutionThe refractive index of a prism is `sqrt(2)`. A ray of light is incident on the prism grazing along one of its refracting surface. What should be the limiting angle of the prism for no emergent ray from the other face?
View SolutionA man with a telescope can just observe the point A on the circumference of the base of an empty cylindrical vessel. When the vessel is filled completely with a liquid of refractive index 1.5, the man can just observe the middle point B of the base of the vessel without moving either the vessel or the telescope. If the diameter of the base of the vessel is 10 cm, what is the height of the vessel?
View SolutionA post of height 4 m is dipped straight in a pond. 1 m of the post remains above the water of the pond. If the rays of the sun are inclined at an angle of `45^(@)` to the surface of water what will be the length of the shadow of the post at the bottom of the pond? Refractive index of water `mu = (4)/(3)`.
View SolutionThere is a point object at a height h above the surface of water in a tank. If the bottom of the tank acts as a plane mirror where will be the image formed? If an observer looks from air at the surface of water normally, calculate the distance of the image from that surface of water of the tank formed by the mirror-like bottom surface of the tank. Refractive index of water `=(4)/(3)`.
View SolutionA rectangular glass slab of thickness 3 cm and of refractive index 1.5 is placed in front of a concave mirror, perpendicular to its principal axis. The radius of curvature of the mirror is 10 cm. Where is an object to be placed on the principal axis so that its image will be formed on the object?
View SolutionA cross mark at the bottom of an empty vessel is focussed with the help of a vertical microscope. Now water `("refractive index" = (4)/(3))` is poured in the vessel. The height of water in the vessel is 4cm. Another lighter liquid which does not mix with water and whose refractive index is `(3)/(2)`, is poured on water. The height of the liquid is 2 cm. How much should the microscope be raised vertically to focus the mark again?
View SolutionA concave mirror of radius of curvature 1 m is placed at the bottom in a reservoir of water. When the sun is situated directly over the head, the mirror forms an image of the sun. If the depth of water is (i) 80 cm and (ii) 40 cm , calculate the image distance from the mirror. `["Given", mu_(w) = (4)/(3)]`
View SolutionThe width of a rectangular glass slab is 5 cm. From a point on its bottom surface, length rays are incident on its top face and after total reflection form a circle of light of radius 8 cm. What is the refractive index of the glass slab?
View SolutionFig.2.61 shows a glass sphere having center at O and two perpendicular diameters AOB and COD. A ray parallel to AOC is incident on the sphere at P where `overset(frown)(AB) = overset(frown)(PC)` and emerges from the sphere at B. Calculate the refractive index of glass and the deviation of the emergent ray.
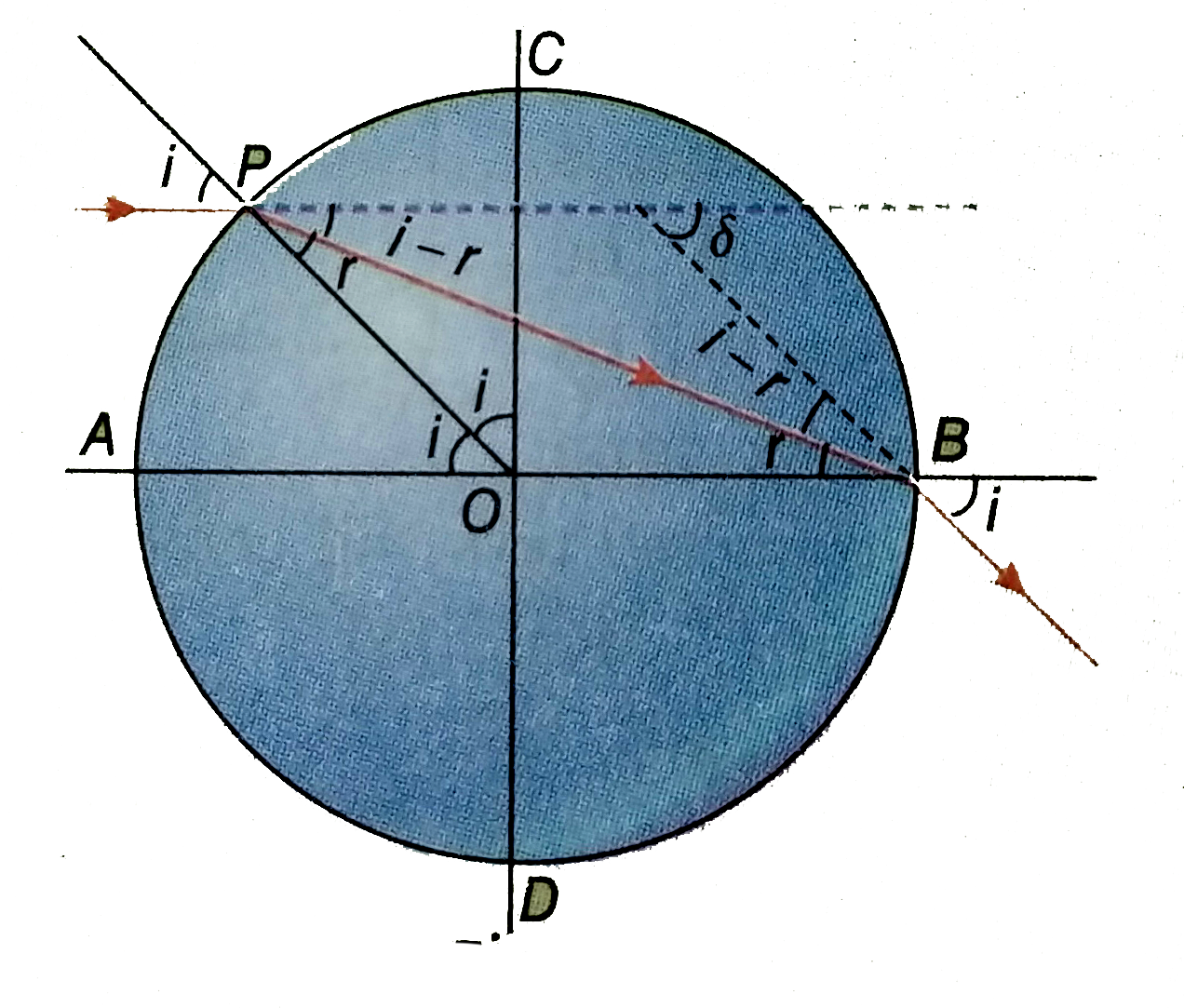
View SolutionA glass slab is placed on a page of a book kept horizontally. What should be the value of the minimum refractive index of the glass slab so that the printed letters of the page will not be visible from any vertical side of the slab?
View SolutionA surface of a prism having refractive index 1.5 is covered with a liquid of refractive index `(3sqrt(2))/(4)` . When be the minimum angle of incidence of an incident ray so that on the other surface of the prism the the ray will be totally reflected from the surface covered with liquid? The refracting angle of the prism `75^(@) [sin48^(@)36' = 0.75].`
View SolutionA ray of light is incident normally on one side of an isosceles right-angled prism and is totally reflected from the other side. (i) What is the value of minimum refractive index of the material of the prism? (ii) If the prism is immersed in water, draw the diagram showing the directing of the emergent ray. In the diagram, point out the values of the angles, `mu` of water `=(4)/(3)`.
View SolutionA ray of light is incident grazing the refracting surface of a prism having refracting angle A. It emerges the other refracting surface making an angle `theta` with the normal to the surface. Prove that the refractive index of the material of the prism is given by `mu = [1+ ((cosA + sintheta)/(sinA))^(-2)]^(1//2).`
View SolutionA ray of light incident normally on a refracting surface of the prism is totally reflected from the other refracting surface. If the prism is immersed in water how will the ray act? Refractive index of glass = 1.5, refractive index of water = 1.33.
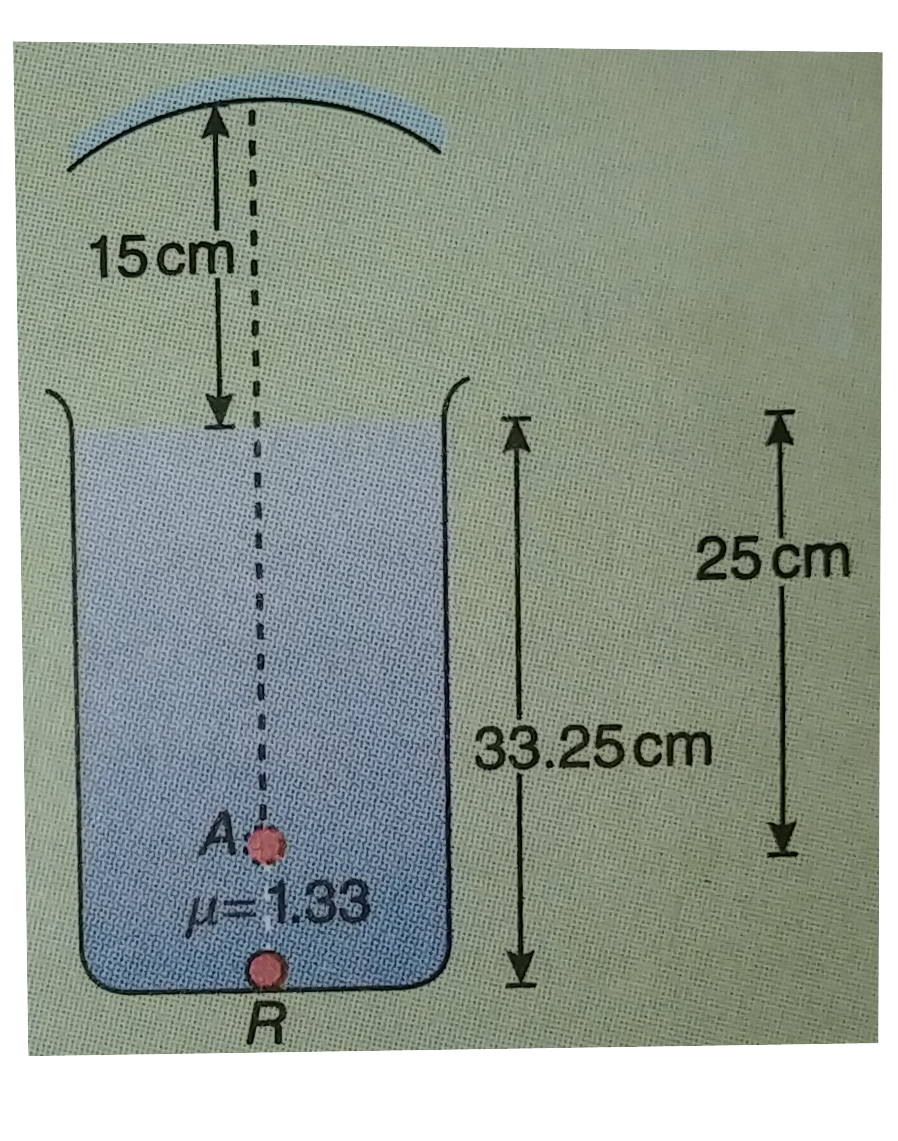
View SolutionA tank of height 33.25 cm is completely filled with liquid `(mu = 1.33)`. An object is placed at the bottom of tank of the axis of concave mirror as shown in the figure. Image of the object is formed 25 cm below the surface of the liquid. What is the focal length of the mirror?
View SolutionWhat should be the minimum value of the refractive index of right angled isosceles prism so that the prism can deviate a ray through `180^(@)` by total internal reflection?
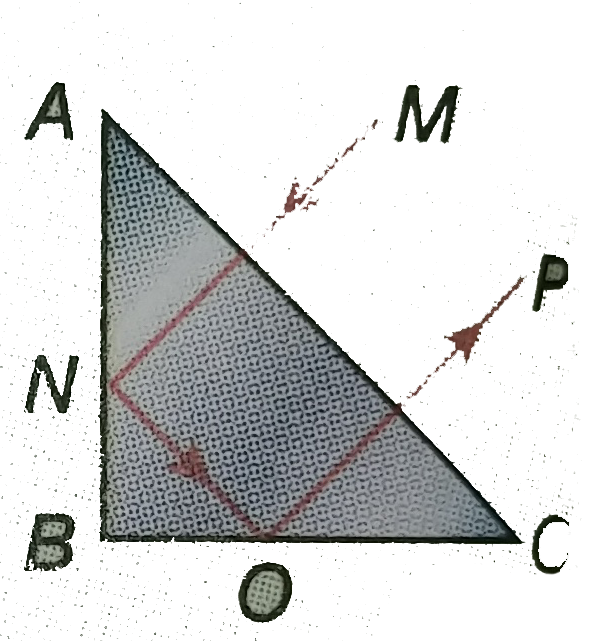
View SolutionThe face of a prism of refracting angle A is coated with silver. A light ray after first being incident at an angle of incidence 2A on the first face of the prism, is refracted and is then reflected from the second face, retracting its path. Calculate the value of the refractive index of the prism.
View SolutionA ray of light falls normally on one side other than the hypotenuse of a right angled isosceles prism of refractive index 1.5. From which side will the ray emerge from the prism? Find the deviation of the incident ray.
View SolutionA vessel contains a liquid of refractive index `(5)/(3)`. Inside the liquid, S is a point source which is observed from above the liquid. An opaque disc of radius 1cm is floating on the liquid such that its centre is just above the source. At this circumstances liquid of the vessel is leaving gradually through a hole. What is the depth of the liquid, so that the source no more remains visible from above?
View Solution
NUMERICAL EXAMPLES questions and complete solutions for chapter REFRACTION OF LIGHT of CHHAYA PHYSICS (BENGALI ENGLISH) of Class 12
All Exercises from CHHAYA PRAKASHINI Class 12 PHYSICS REFRACTION OF LIGHT
- AIMPT
- CBSE SCANNER
- Comprehension type
- ENTRANCE CORNER
- EXAMINATION ARCHIVE WITH QUESTION
- EXERCISE Short Answe Type Question - II
- EXERCISE MULTIPLE CHOICE QUESTION
- EXERCISE Short Answer Type Question - 1
- EXERCISE Very Short Answer or two Question (Mark1)
- HIGHER ORDER THINKING SKILL (HOTS QUESTION)
- Hots Numerical Problems
- Integer answer type
- JEE MAIN
- Multiple correct answer type
- NCERT EXEMPLAR QUESTIONS WITH ANSWER HINT
- NCERT TEXTBOOK QUESTION WITH ANSWER HINT
- NEET
- NUMERICAL EXAMPLES
- Problem set - I
- Problem set - II
- SECTION RELATED QUESTION
- WBJEE