Complete Solutions to Exercises of chapter ELECTRIC FIELD AND POTENTIAL of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTRIC FIELD AND POTENTIAL |
| HC VERMA | Exercises |
| Number Of Questions | 75 |
| Academic Year | 2023-24 |
Find the dimensional formula of `epsilon_0` .
View SolutionA charge of 1.0 C is placed at the top of your college building and another equal charge at the top of your house. Take the separaton between the two charges to be 2.0 km. Find the force exerted by the charges on each other. How many time of your weight is this force?
View SolutionAt what separation should two equal charges 1.0 C each, be placed so that the force between them equals the weight of a 50 kg person?
View SolutionTwo equal charges are placed at a separtion of 1.0 m. What should be the magnitude of the charges so that the force between them equals of a 50 kg person?
View SolutionFind the electric force between two protons separated by a distance of 1 fermi `(1fermi = 10^(15)m).` The protons in a nucleus remain at a separation of this order.
View SolutionTwo chargea `2.0xx10^(-6) C` are placed at a separation of 10 cm. where should a third charge be placed such that it experiences no net force due to these charges.
View SolutionSuppose the second charge in the previous problem is `-1.0 xx 10^(-6) C.` Locate the position where a third charge will not experience a net force.
View SolutionTwo charged particles are placed at a distance 1.0 cm apart. What is the minimum possible magnitude of the electric force acting o each charge?
View SolutionEstimate the number of electrons in 100 g water. How much is the total negative charge on these electrons?
View SolutionSuppose all the electrons of 100 g water are lumped together to form a negatively charged particle and all the nuclei are lumped together to form a positively charge particle. If these two particles are placed 10.0 cm away from each other, fien the force of attraction between them. Compare it with your weight.
View SolutionConsider a gold nucleus to be a sphere of redius 6.9 fermi in whichprotons and neutrons are distributed. Find the force of repulsion between two protons situated at largest separaton. Why do thes protons not fly apart under this repulsion
View SolutionTwo insulating small spheres are rubbed against each other and placed 1 cm apart. If they attract each other with a force of 0.1 N, how many electrons were transferred from one sphere to the other during rubbing?
View SolutionNa Cl moecule is bound due to the electreic force between the sodium and the chlorine ions when one electron of sodium and the chlorine ions when one electron of sodium is transferred to chlorine. Taking the separaton between the ions to be `2.75xx10^(-8) cm,` find the force of attraction between them. State the assumptions (if any) that you have made.
View SolutionFind the ratio of the electric and gravitational forces between two protons.
View SolutionSuppose ana attractive nuclear force acts between two protons which may be written as `F = Ce^(-kr) //r^2,` (a) Write down the dimensional formulae and appporpriate SI units of C and k. (b) Suppose that `k = 1 fermi^(-1)` and that the repulsive electreic force between the protons is just blanced by the attractive nuclear force when the separation is 5 fermi. Find the value of c.
View SolutionThree equal charges, `2.0xx 10^(-6)` C each, are held fixed at the three corners of a square of side 5 cm. find the Coulomb force experienced by one of the charges due to the rest two.
View SolutionFour equal charges `2.0xx10^(-6) C` each are fixed at the four corners of a squae of side 5 cm. Find the coulomba force eperienced by one of the charges due to the rest three.
View SolutionA hydrogen atom contains one proton and one electron. It may be assumed that the electron revolves in a circle of radius 0.53 angstrom `(1 angstrom = 10^(-10)` m and is abbreviated as A) with the proton at the centre. The hydrogen atom is said to be in the ground state in this case. Find the magnitude of the electric force between the proton and the electron of a hydrogen atom in its ground state.
View SolutionFind the speed of the electron in the ground state of hddrogen atom. The description of ground state is given in the previous problem.
View SolutionTen positively charged particles are kept fixed on the x-axis at points x=10cm, 20cm, 30cm, …, 100cm. The first particle has a charge `1.0xx 10^(-8)C`, the second `8xx10^(-8)` C, the third `27xx10(-8)`C and so on. The tenth particle has a charge `1000xx10^(-8)C.` find the magnitude of the electric force acting on a 1 C charge placed at the origin.
View SolutionTwo charged particles having charge `2.0xx 10^(-8)C` each are joined by an insulating string of length 1 m and the system is kept on a smooth horizontal table. Find the tension in the string.
View SolutionTwo indentical balls, each having a charge of `2.00xx10^(-7) C` and a mass of 100g , are suspended from a common point by two insulating strings each 50 cm long. The balls are held at a separation 5.0cm apart and then released. Find (a) the electric force on one of the charged balls (b) the components of the resultant force on it alongand perpendicular to the string (c) the tension is the string (d) the components of the resultant force on it along and perpendicular to the string(c) the tension in the string (d) the acceleration of one of the balls. Answers are to be obtained just after the release.
View SolutionTwo identical pith balls are charged by rubbing against each other. They are suspended from a horizontal rod through two strings of length 20 cm each, the separation between the suspension points being 5 cm. in equilibrium, the separation between the balls in 3 cm. Find the mass of each ball and the tension in the strings. the charge on each ball a magnitude `2.0 xx 10^(-8) C.`
View SolutionTwo small spheres, each having a mass of 20 g, are suspended form a common point by two insulating strings of length 40 cm each. The spheres are identically charged and the speration between the balls at equilibrium is found to be 4 cm . Find the charge on each sphere.
View SolutionTwo indentical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is `2theta` in equilibrium.
View SolutionA particle having a charge of `2.0xx10^(-4) C` is placed directly below and at a separtion of 10 cm from the bob of a simple pendulum at rest. The mass of the bob is 100g. What charge should the bob be given so that the string becomes loose?
View SolutionTwo particles A and B having charges q and 2q respectively are placed on a smooth table with a separation d. A third particle C is to be clamped on the table in such a way that the particles A and B remain at rest on the table under electrical forces. What should be the charge on C and where should it clamped?
View SolutionTwo identically charged particles are fastened to the two ends of a spring of spring constant `100 N m ^(-8) C,` find the extension In the length of the apring. Assume that the extension is small as scompared to the natural length . Justify this assumption after you solve the problem.
View SolutionA particle A having a charge of `2.0xx10 ^(-6) C` is held fixed on a horizontal table. A second charged jparticle of mass 80g stays in equilibrium on the table at a distance of 10 cm from the firsst charge. The coefficient of friction between the table and this second jparticle is `mu = 0.2`. find the range within which the charge of this second particle may lie.
View SolutionA particle A having a charge of `2.0xx 10^(-6)` C and a mass of 100 g is placed at the bottom of a smoth inclined plane of inclination `30@` . Where should another particle B, having same charge and mass, be placed on the incline so that it may remain in equilibrium?
View SolutionTwo particles A and B having equal charges are placed at distance d apart. A third charged particle placed on the perpendicular bisector at a distance x will experience the maximum Coulomb’s force when :
View SolutionTwo particles A and B , each carrying charge Q are held fixed with a separation D between them. A particle C having mass m and charge q is kept at the middle point of the line AB.
(a) If it is displaced throught a distance x perpendicular to AB, what would be the electric force experienced by it .
(b) Assuming x little, show that this force is proportional to x.
(c) under what conditions will the paricle C execute simple harmonic motion if it is released after such a small displacement? Find the time period of the oscillations if these conditions are stisfied.
View SolutionRepeat the previous problem if the particle C s displaced through a distance x along the line AB.
View SolutionThe electric force experienced by a charge of `1.0xx10^(-6) C is 1.5 xx 10^(-3) N . Find the magnitude of the electric field at the position of the chaerge.
View SolutionTwo particles A and B having charges of `+2.00 xx 10^(-6) C` and of `- 4.00xx 10^(-6)` respectively are held fixed at a separation of 20.0 cm . Locate the point(s) on the line AB where (a) the electric field is zero (b) the electric potential is zero.
View SolutionA Point charge produces an electric field of room ? What is its direction?
View SolutionA water particle of mass 10.0 mg and having a charge of `1.50 xx 10^(-6)C` stays suspended in a room. What is the magnitude of electric field in the room ? What is its direction?
View SolutionThree identical charges, each having a value `1.0 xx10^(-8)C,` are placed at the corners of an equilateral triangle of side 20 cm find the electric field and potential at the centre of the triangle.
View SolutionPositive charge Q is distributed uniformly over a circular ring of radius R. A particle having a mass m and a negative charge q, is placed on its axis at a distance x from the centre. Find the force on the particle. Assuming x ltltR, find the time period of oscillation of the particle if it is released from there.
View SolutionA rod of length L has a total charge Q distributed uniformly along its length. It is bent in the shape of a semicircle. Find the magnitude of the electric field at the centre of curvature of the semicircle.
View SolutionA 10 cm long rod carries a charge of `+150 muC` distributed uniformly along its length. Find the magnitude of the electric field at a point 10 cm from both the ends of the rod.
View SolutionConsider a uniformly charged ring of radius R. Find the pint on the axis where the electrie field is maximum.
View SolutionA wire is bent in the form of a regular hexagon and a total charge q is distributed uniformly on it. What is the electric field at the centre? You may answer this part without making any numerical calculations.
View SolutionA circular wire-loop of radius a carries a total charge Q distributed uniformly over its length . A small length dL of the wire is cut off. Find the electric field at the centre due to remaining wire.
View SolutionA positive charge q is placed in front of cinducting solid cube at a distance d from its centre. Find the electric field at the centre of the cube due to the charges appearing on its surface.
View SolutionA pendulum bob of mass 80mg and carrying a charge of `2xx 10^(-8)C` is at rest in a uniform, horizontal electric field of 20k `Vm^-1.` Find the tension in the thread.
View SolutionA particle of mass m and charge q is thrown at a speed u against a uniform electric field E. How much distance will it travel before coming to momentary rest?
View SolutionA particle of mass 1 g and charge `2. 5 xx10^(-4) C` is released from rest in an electric field of `1.2 xx 10^4 NC^(-1)` (a) Find the electric force and the force of gravity acting on this particle. Can one of these forces be neglected in comparison with the other for approximate analysis? (b) How long will it take for the particle to travel a distance of 40 cm? (c) What will be the speed of the particle after travelling this destance? (d) how much is the work done by electric force on the particle during this period?
View SolutionA ball of mass 100g and having a charge of `4.9xx 10^(-5)` C is released from rest in a region where a horizontal electric field of `2.0 xx 10^4 NC^(-1)` exists. (a) find the resultant force acting on the ball. (b) What will be the path of the ball ? (c ) Where will the ball be at the end of 2 s?
View SolutionThe bob of a simple pendulum has a mass of 40 g and a positive charge of `4.0 xx 10 ^(-5) C` . It makes 20 oscillations in 45 s. A vertical electric field pointing upward and of magnitude `2.5 xx 10^ 4 NC^(-1)` is switched on. How much time will it now take to complete 20 oscillations?
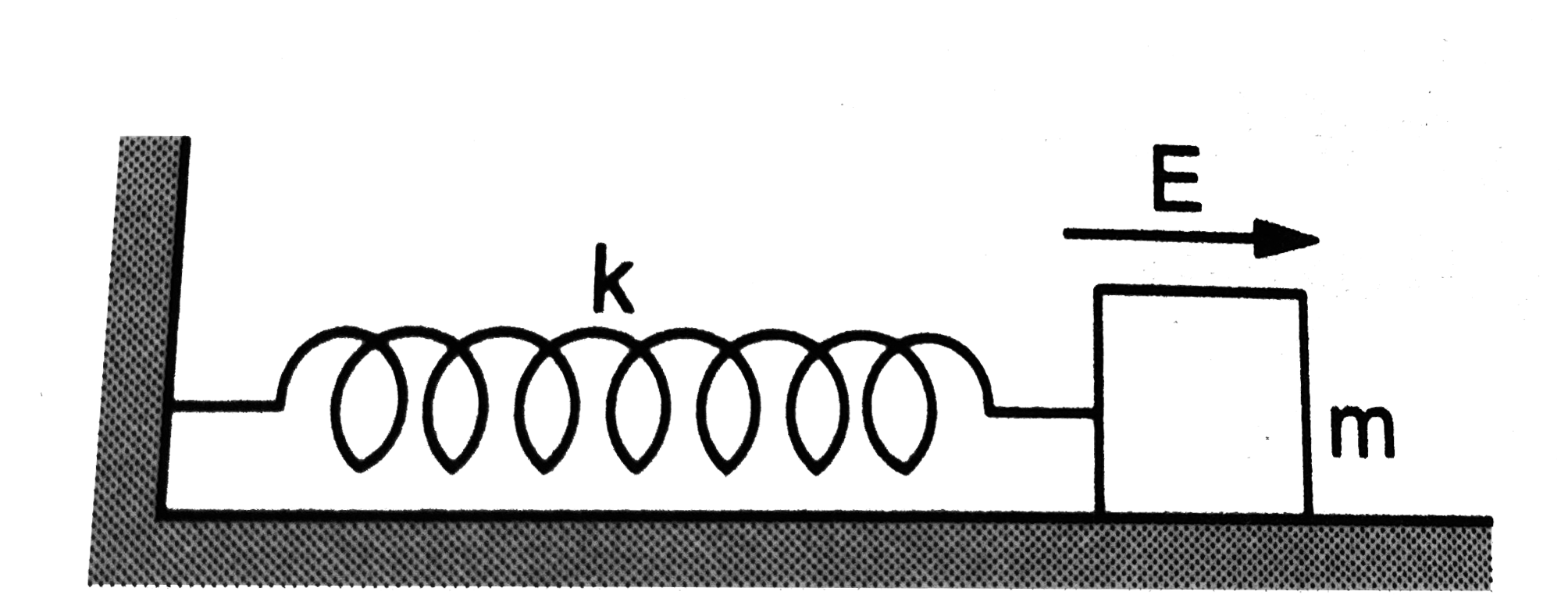
View SolutionA block of mass m having a charge q is placed on a smooth horizontal table and is connected to a wall through an unstressed spring of spring constant k as shown in figure(29.E1) . A horizontal electric field E parallel to the spring is switched on. Find the amplitude of the resulting SHM of the block.
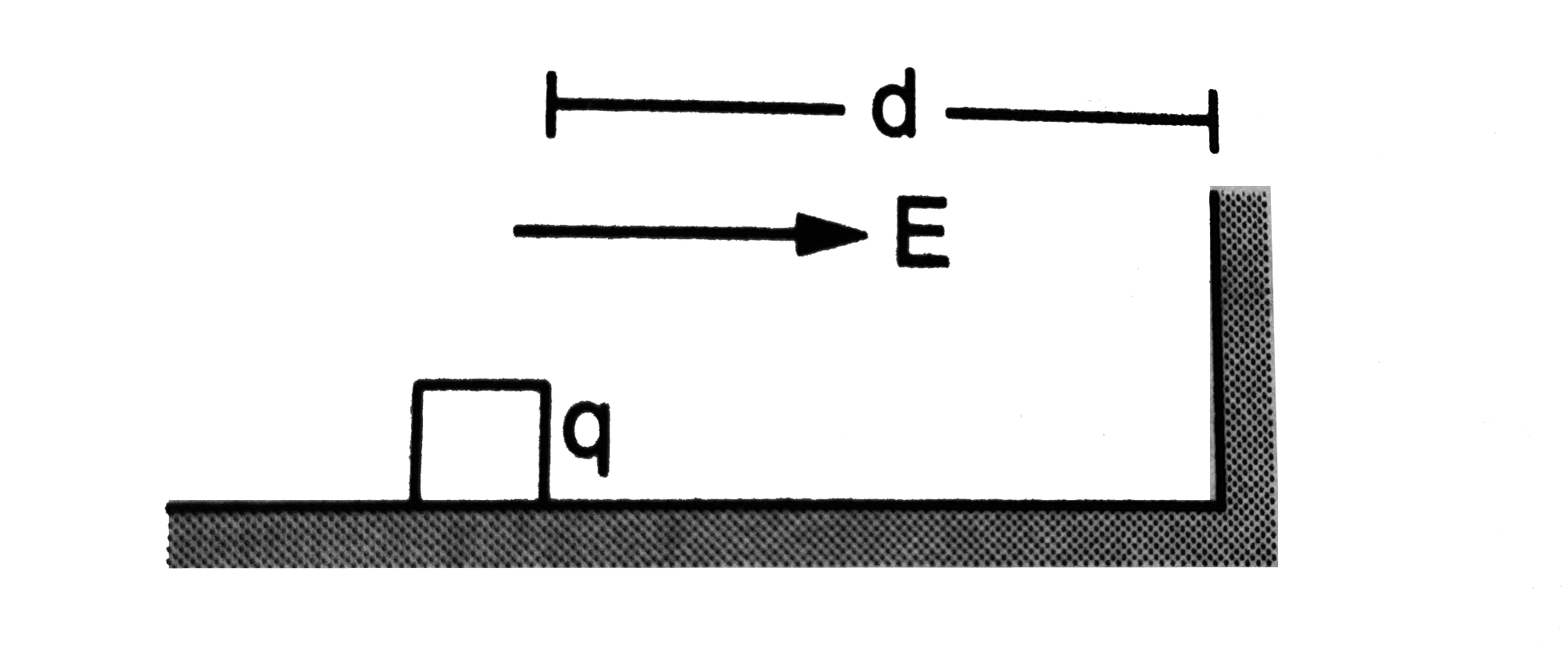
View SolutionA block of mass n containing a net positive charge q is placed on a smooth horizontal table which terminates in a vertical wall as shown in figure(29-E2). The distance of the bolck from the wall is d. A horizontal electric field E to towards right is switched on. Assuming elastic collisions find the time period of the resulting oscillatory motio. Is it a simple harmonic motion?
View SolutionA Uniform electric field of `10NC ^(-1)` exists in the vertically downward direction. Find the increase in the electric potential as one goes up through a height of 50cm.
View Solution12 j of work has to be done against an existion electric field to take a charge of 0.01 C from A to B. How much is th potential difference `V_B V_A?`
View SolutionTwo equal charges, `2.0xx10^(-7) C` each, are held fixed at a separation of 20cm. A third charge of equal magnitude is placed midway between the two both the charges. How much work is done by the electric field during the process?
View SolutionAn electric field of `20 N//C` exists along the x-axis in space. Calculate the potential difference `V_B - V_A` where the points A and B are given by
a. `A=(0,0), B=(4m, 2m)`
b. `A=(4m,2m),B=(6m,5m)`
View SolutionConsider the situation of the previous problem. A charge of `2.0xx 10 ^(-4) C` is moved from the point A to the point B. find the change in electrical potential energy `U_B-U_A` for the cases (a) , (b) and ( c ).
View SolutionAn electric field `vecE = vec(i20 + vecj30 ) NC^(-1)` exists in the space. If the potential at the origin is taken to be zero find the potential at (2m, 2m).
View SolutionAn electric field `vecE = vec I Ax` exists in the space, where `A= 10 V m ^(-2).` Take the potential at (10m, 20m ) to be zero. Find the potential at the origin.
View SolutionThe electric potential existing in space is `V(x,y,z)= A (xy+ yz+zx)`.(a) Write the dimensional A. (b) find the expression for the electric field.( c ) If A is 10 SI units, find the magnitude of the electric field at (1m, 1m, 1m).
View SolutionTwo charged particles, having equal charges of `2.0xx 10^(-5) C` each, are brought from infinity to within a separation of 10 cm. Find the increase in the electric potential energy during the process.
View SolutionSome equipotential surfaces are shown in figure(29.E3) What can you say about the magnitude and the direction of the electric field?

View SolutionConsider a circular ring of radius r, uniformly charged with linear charge density `lambda`. Find the electric potential aty a point on the exis at a distance x from the centre of the ring. Using this expression for the potential, find the electric field at this point.
View SolutionAn electric field of magnitude `1000 NC ^(-1)` is produced between two parallel platees having a separation of 2.0 cm as shown in figure(29.E4) (a) What is the potential difference between the plates? (b) With what minimum speed should an electron be projected from the lower plate in the direction of the field so that it may reach the upper plate? ( c) Suupose the electron is projected from the lower plate with the speed calculated in part (b) . The direction of projection makes an angle of `60@` with the field. Find the mazimum height reached by the electron.

View SolutionA uniform field of `2.0 NC^(-1)` exists in space in x direction (a) Taking the potential at the origin to be zero, write an experssion for the potential at a general point (x,y,z). (b) At which points, the potential is 25V ? ( c) If the potential at the origin is taken to be 100V , what will be the expression for the potential at a general point? (d) What will be the potential at the origin if the potential at infinity is taken to be zero ? Is it parctical to choose the potential at infinity to be zero?
View SolutionHow much work has to be done in assembling three charged particles at the vertices of an equilateral triangle as shown in figure

View SolutionThe kinetc energy of a chargd particle decreased by 10 J as it moves from a point at potential 100 V to a point at potential 200V . Find the charge on the particle.
View SolutionTwo identical particles, each having a charge of `2.0xx10^(-4) C` and then released. What would be the speeds of the particles when the separtion becomes large?
View SolutionTwo particles have equal masses of 5.0 g each and opposite charges of `+4.0 xx10^(-5) C.` They are released from rest with a separation of 1.0 m between them. Find the speeds of the particles when the separation is reducced to 50 cm.
View SolutionA smple of HCl gas is placed in an electric field of `2.5xx 10^4 NC^(-1)`. The dipole moment of each HCl molecule is `3.4 X 10^(-30) Cm.` find the maximum torque that can act on a molecule.
View SolutionTwo particles A and B, having opposite charges`2.0xx 10^(-6)` and `-2.0 xx10^(-6)`C , are placed at a separaton of 1.0 cm.(b) Calculate the electric field at a point on the axis of the dipole 1.0 m away from the centre. (c ) Calculate the electric field at a point on the perpendicular bisector of the dipole and 1.0 m away from the centre.
View SolutionThree charges are arranged on the vertices of an equilateral triangle as shown in figure (29.E6) find the dipole moment of the combination.

View Solutionfind the magnitude of the electric field at the point P in the configuration shown in figure for `dgtgta, Take2qa = p.`
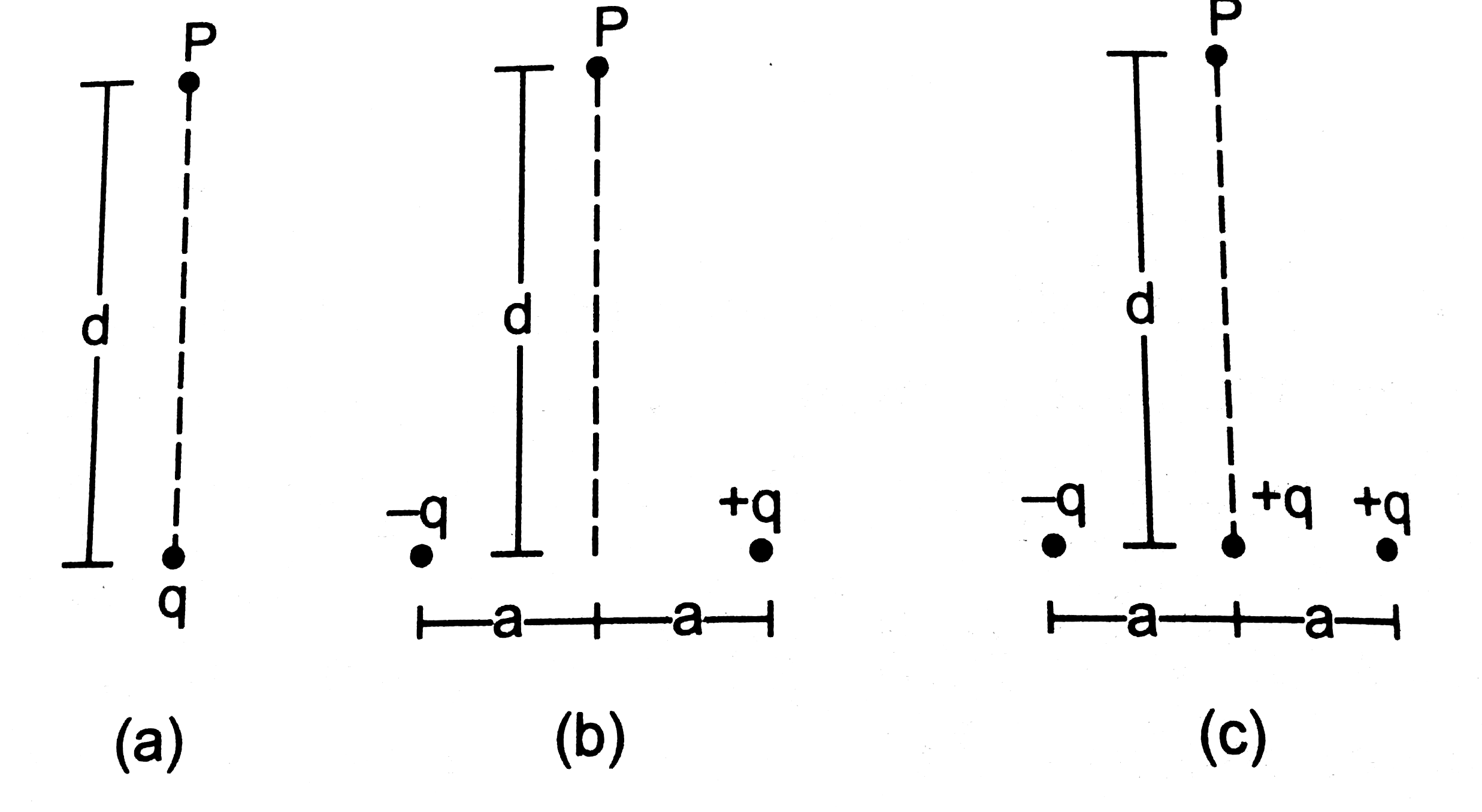
View SolutionTwo particles, carrying charges -q and +q and having equal masses m each, are fixed at the rod is clamped at an end and is placed in a uniform electric field E with the axis of the dipole along the electric field. The rod is slightly tlted and then released. Neglecting gravity find the time period of small oscillations.
View SolutionAssume that each atom in a copper wire contributes one free electron. Estimate the numberof free electrons in a cpper wire having a mass of 6.4g (take the atomic weight of copper ot be 64g `mol^(-1).`
View Solution
Exercises questions and complete solutions for chapter ELECTRIC FIELD AND POTENTIAL of HC VERMA PHYSICS (HINGLISH) of Class 12