Complete Solutions to Exercise 2 of chapter APPLICATIONS OF DEFINITE INTEGRALS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | APPLICATIONS OF DEFINITE INTEGRALS |
| MHTCET PREP GUIDE | Exercise 2 |
| Number Of Questions | 34 |
| Academic Year | 2023-24 |
Find the area under the curve `y = sqrt(x-1)` in the interval [1, 5] between the lines x = 1 and x = 5, is
View SolutionIf a curve `y = asqrt(x)+bx` passes through the point (1,2) and the area bounded by the curve, line x = 4 and X-axis is 8 sq units, then
View SolutionWhat is the area bounded by the curves `y=e^x ,y =e ^-x` and the straight line `x=1` ?
View SolutionThe area between the curve `y=2x^(4)-x^(2)`, the x-axis, and the ordinates of the two minima of the curve is
View SolutionThe area bounded by the curve `y =ln(x)` and the lines `y = 0, y =ln(3)` and `x = 0` is equal to
View SolutionThe area bounded between the parabolas `x^2=y/4"and"x^2=9y` and the straight line `y""=""2` is (1) `20sqrt(2)` (2) `(10sqrt(2))/3` (3) `(20sqrt(2))/3` (4) `10sqrt(2)`
View SolutionThe area of the figure bounded by the curves `y^(2)=2x+1` and `x-y-1=0` , is
View SolutionThe area of the plane region bounded by the curves `x + 2y^(2)=0` and `x+3y^(2)=1` is equal to
View SolutionThe area enclosed between the curves `y = x^(3)` and `y = sqrt(x)` is
View SolutionThe area enclosed between the parabola `y = x^(2)-x+2` and the line y = x + 2 (in sq unit) equals to
View SolutionThe area bounded by the curves `y^(2)=4a^(2)(x-1)` and lines x = 1 and y = 4a is
View SolutionThe area bounded by the curves y = cos x and y = sin x between the ordinates x = 0 and `x = (3pi)/(2)`, is
View SolutionThe area of the plane region bounded by the curve `x = y^(2)-2` and the line y = - x is (in sq units)
View SolutionThe area bounded by the curve `y = 2x - x^(2)` and the line y = - x is
View SolutionFor `0 lt= x lt= pi,` the area bounded by `y = x` and `y = x + sin x,` is
View SolutionIf the area above the x-axis, bounded by the curves `y = 2^(kx)` and x = 0, and x = 2 is `3/(log_e(2))`, then the value of k is
View SolutionThe area of the region described by `A = {(x,y) : x^2 + y^2 lt= 1and y^2 lt= 1- x}` is
View SolutionThe area in the first quadrant between `x^2+y^2=pi^2` and `y=sinx` is
View SolutionThe area bounded by the curves `y=sqrtx, 2y-x+3=0,` X-axis and lying in the first quadrant is
View SolutionThe area bounded by y = |sin x|, X-axis and the line `|x|=pi` is
View SolutionFind the area bounded by the x-axis, part of the curve `y=(1-8/(x^2))` , and the ordinates at `x=2a n dx=4.` If the ordinate at `x=a` divides the area into two equal parts, then find `adot`
View SolutionThe area bounded by the graph of `y=f(x), f(x) gt0` on [0,a] and x-axis is `(a^(2))/(2)+(a)/(2) sin a +(pi)/(2) cos a ` then find the value of `f((pi)/(2))`.
View SolutionThe line `x = (pi)/(4)` divides the area of the region bounded by y = sin x, y = cos x and X-axis `(0lexle(pi)/(2))` into two regions of areas `A_(1)` and `A_(2)`. Then, `A_(1) : A_(2)` equals
View SolutionThe area bounded by the curve `y=x|x|`, x-axis and the ordinates x=1,x=-1 is given by
View SolutionThe area (in sq units) of the region bounded by the curves `y = e^(x)`, `y = log_(e)` x and lines x = 1, x = 2 is
View SolutionThe area (in sq units) of the region described by `{(x,y):y^(2)le2x and yge4x-1}` is
View SolutionThe larger of the area bounded by y = cosx, y = x + 1 and y = 0 is
View SolutionThe parabola `y^2 = 2x` divides the circle `x^2 + y^2 = 8` in two parts. Then, the ratio of the areas of these parts is
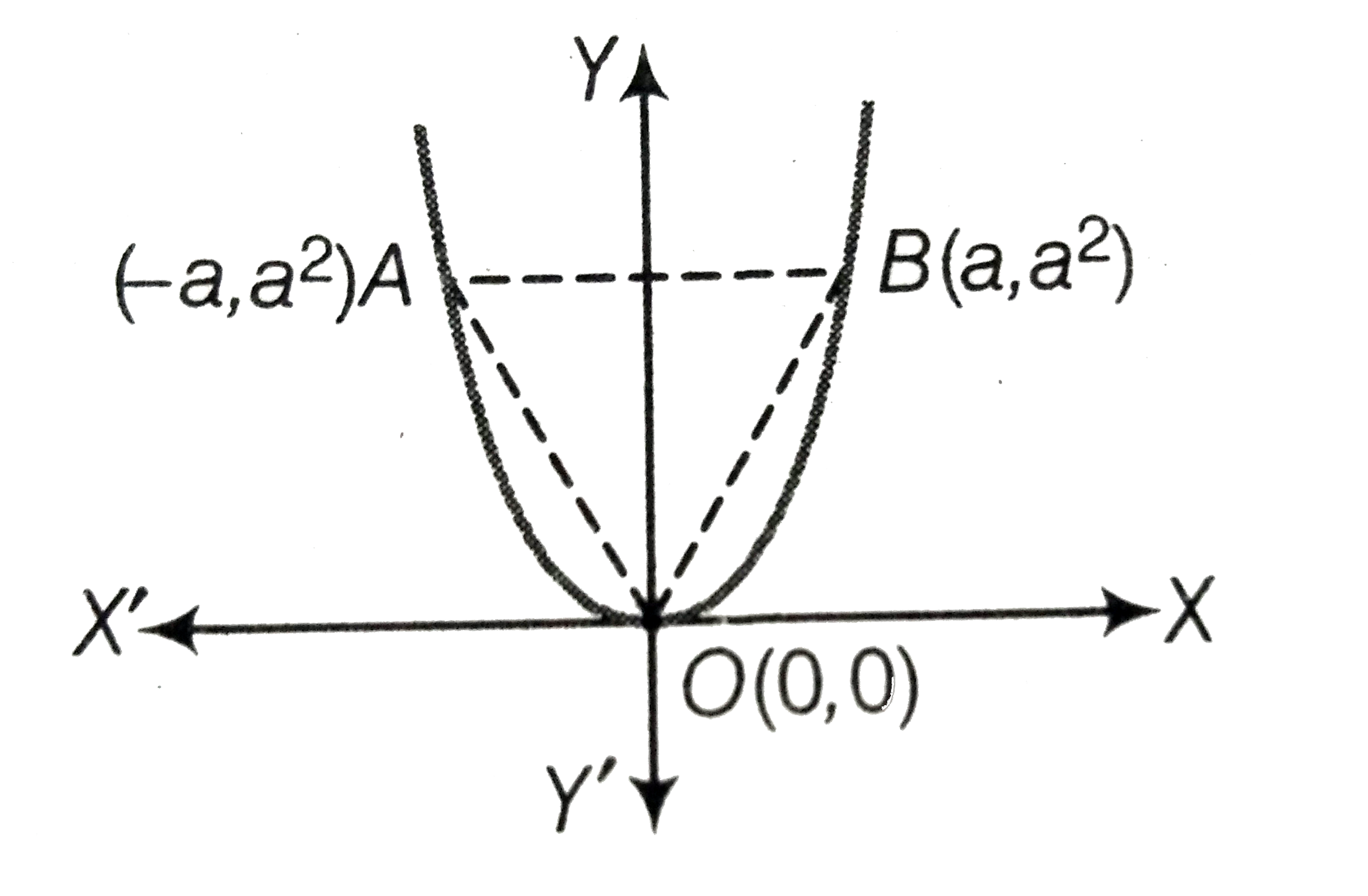
View SolutionThe figure shows a `DeltaAOB` and the parabola `y = x^(2)`. The ratio of the area of the `DeltaAOB` to the area of the region AOB of the parabola `y = x^(2)` is equal to
View SolutionThe area bounded by `y = sin^(-1)x,x=(1)/(sqrt(2))` and X-axis is
View SolutionFind the area of the region bounded by the ellipse `(x^(2))/(9)+(y^(2))/(4)=1` in fourth quadrant.
View SolutionThe area bounded by the curves `y^(2)=4a(x+a)` and `y^(2)=4b(b-x)`, where `a, bgt0` units
View SolutionFind the area bounded by the curve `y=2x-x^2` and the straight line `y=-x`
View SolutionFind the area of the smaller region bounded by the ellipse `(x^2)/9+(y^2)/4=1` and the line `x/3+y/2=1`
View Solution
Exercise 2 questions and complete solutions for chapter APPLICATIONS OF DEFINITE INTEGRALS of MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS of Class 12