Complete Solutions to Level III (C.W) of chapter ELECTROSTATICS AND GAUSS LAW of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTROSTATICS AND GAUSS LAW |
| NARAYANA | Level III (C.W) |
| Number Of Questions | 55 |
| Academic Year | 2023-24 |
A ball of mass `m=0.5kg` is suspended by a thread and a charge `q=0.1muC` is supplied when a ball with diameter `5cm` and a like charge of same magnitude is brought close to the first ball but below it the tension decreases to `1//3` of its intial value .The distance between centres of the balls is
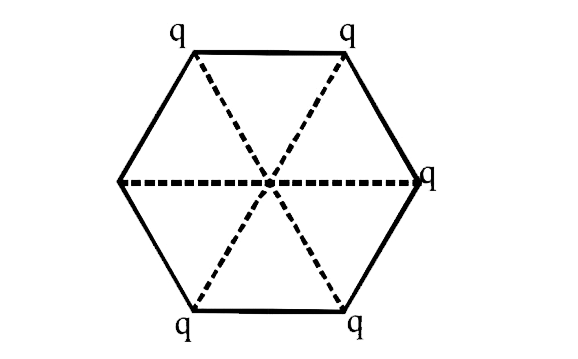
View SolutionFive point charges, each of value +q coul, are placed on five vertices of a regular hexagon of isde L meters. The magnitude of the force on the point charge of value -q coul, placed at the centre of the hexagen is…………….
View SolutionTwo small objects `X` and `Y` are peramanently separated by a distance `1cm` .Object `X` has a charge of `+1.0muC` and object `Y` has a charge of `-0.1muC` ,A certain number of electrons are removed from `X` and put onto `Y` to make the electronstatic force between two objects an attractives force whose magnitude is `360N` Number of electrons removed is
View SolutionTwo identical positive charges are fixed on the y-axis, at equal distances from the origin O. A particle with a negative charges starts on the x-axis at a large distance from O. moves along the x-axis passes through O, and moves far away from O on the other side. Its acceleration a is taken as positive along its direction of motion. Plot acceleration a of the particle against its x-coordinate.
View SolutionTwo equal negative charges `-q` are fixed at points `(0, -a)` and `(0,a)` on y-axis. A poistive charge Q is released from rest at point `(2a, 0)` on the x-axis. The charge Q will
View SolutionIn a liquid medium of dielectric constant `K` and of spherical gravity `2` two identically charged spheres are suspended from a fixed point by threads of equal length .The angle between them is `90^(@)` .In another medium of unknown dielectric constant `K^(1)` and specific gravity `4` the angle between them become `120^(@)` if density of material of spheres is `8gm//c c` then` K^(1)` is
View SolutionThe force of attraction between two charges separated by certain distance in air is `F_(1)` .If the space between the charges is completely filled with dielectric of constant `4` the force becomes `F_(2)` .If half of the distance between the charges is filled with same dielectric the force between the charges is `F_(3)` Then `F_(1):F_(2):F_(3)` is
View SolutionTwo small spheres of masses `M_(1)`and `M_(2)` are suspended by weightless insulating threads of lengths `L_(1)` and `L_(2)`. The spheres carry charges `Q_(1)` and `Q_(2)` respectively. The spheres are suspended such that they are in level with one another and the threads are inclined to the vertical at angles `theta_(1)` and `theta_(2)`respectively . Which one of the following conditions is essential for `theta_(1) = theta_(2)` ?
View SolutionIf the electric field between the plates of a cathode ray oscilloscope be `1.2xx10^(4)N//C` ,the deflection that an electron will experience if it enters at right angels to the field with kinetic energy `200eV` is (the defelction assembly) is `1.5cm` long
View SolutionIf the electric field between the plates of a cathode ray oscilloscope be `1.2xx10^(4)N//C` ,the deflection that an electron will experience if it enters at right angels to the field with kinetic energy `200eV` is (the deflection assembly is `1.5cm` long)
View SolutionA bob of a simple pendulum of mass `40gm` with a positive charge `4xx10^(-6)C` is oscillating with a time period `T_(1)`.An electric field of intensity `3.6xx10^(4)N//C` is applied vertically upwards.Now the time period is `T_(2)` the value of `(T_(2))/(T_(1))` is `(g=10//s^(2))`
View SolutionA particle of mass m and charge q is released from rest in uniform electric field of intensity E. Calculate the kinetic energy it attains after moving a distance x between the plates.
View SolutionFour equipotnetial curves in an electric filed are shown in the figure `A,B,C` are `E_(A),E_(B),E_(C)` then

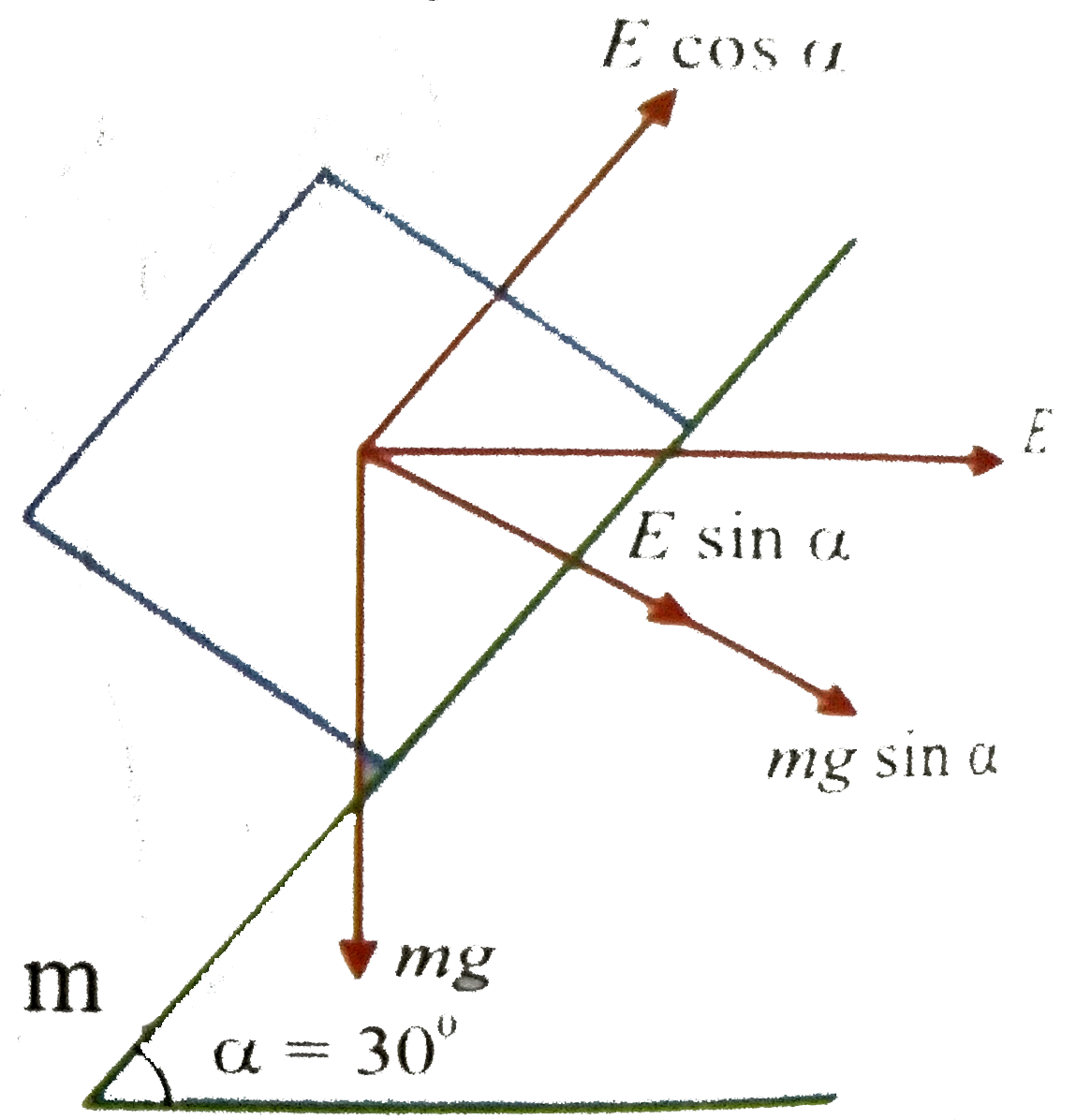
View SolutionA partical of mass `1kg` and carrying `0.01C` is at rest on an inclined plane of angle `30^(@)` with horizontal when an electric field of `(490)/(sqrt(3))NC^(-1)` applied parallel to horizontal .The cofficient of friction is
View SolutionElectric field on the axis of a small electric dipole at a distance r is `vec(E)_(1)` and `vec(E)_(2)` at a distance of `2r` on a line of perpendicular bisector is
View SolutionA particle having charge that of an electron and mass `1.6xx10^(-30)`kg is projected with an initial speed u at the angle `45^(@)` to the horizontal from the lower plate of a parallel-plate capacitor as shown in fig. The plates are sufficiently long and have a separation of 2 cm, find the maximum value of the velocity of he particle so that it does not hit the upper plate. Take the electric field between the plates as `10^(3)Vm^(-1)` directed upward.

View SolutionA thin copper ring of radius `a` is charged with `q` units of electricity.An electron is placed at the centre of the copper ring .If the electron is displaced a little, it will have frequency
View SolutionA thin fixed of radius 1 metre has a positive charge `1xx10^-5` coulomb uniformly distributed over it. A particle of mass 0.9 gm and having a negative charge of `1xx10^-6` coulomb is placed on the axis at a distance of 1cm from the centre of the ring. Show that the motion of the negatively charged particle is approaximately simple harmonic. Calculate the time period of oscillations.
View SolutionA spheres carrying charge `0.01C` is kept at rest without falling down ,touching a wall by applying an electric filed `100N//C`.If the coefficient of friction between the sphere and the wall is `0.2` the weight of the sphere is
View SolutionA particles of mass `1kg` and carrying positive charge `0.01C` is sliding down an inclined plane of angle `30^(@)` with the horizontal .An electric field `E` is applied to stop the particles.If the coefficient of friction between the particles and the surface of the plane is `(1)/(2sqrt(3))` E must be
View SolutionTwo ideantical point charges are placed at a separation of `d`. `P` is a point on the line joining the charges, at a distance `x` from any one charge. The field at `P` is `E, E` is plotted against `x` for value of `x` from close to zero to slightly less then `d`. Which of the following represents the resulting curve
View SolutionA particle of charge `-q` and mass `m` moves in a circular orbits of radius `r` about a fixed charge `+Q`.The relation between the radius of the orbit `r` and the time period `T` is
View SolutionA thin semi-circular ring of radius r has a positive charge q distributed uniformly over it. The net field `vecE` at the centre O is
View SolutionTwo thin wire rings each having radius R are placed at distance d apart with their axes coinciding. The charges on the two are `+Q` and `-Q`. The potential difference between the centre so the two rings is
View SolutionTwo metal sphres `A` and `B` have their capacities in the ratio `3:4` they are put in contanct with each other and an amount of charge `7xx10^(-6)C` is given to the combination .Next the two spheres are spearated and kept wide the apart so that one has no elecrtrical influence on the other.The potential due to the smaller sphere at a distance of `50m` from it is
View SolutionA solid conducting sphere having a charge Q is surrounded by an uncharged concentric conducting hollow spherical shell. Let the potential difference between the surface of the solid sphere and that of the outer surface of the hollow shell be V. If the shell is now given a charge of `-3Q`, the new potential difference between the same two surfaces is :
View SolutionA spherical charged conductor has surface charge density `sigma`.The intensity of electric field and potential on its surface are `E` and `V` .Now radius of sphere is halved keeping the charge density as constant .The new electric field on the surface and potneial at the centre of the sphere are
View SolutionTwo spherical conductors A and B of radii 1mm and 2mm are separated by a distance of 5 cm and are uniformly charged. If the spheres are connected by a conducting wire then in equilibrium condition, the ratio of the magnitude of the electric fields at the surfaces of spheres A and B is
View SolutionA charge `+q` is fixed at each of the points `x=x_0`, `x=3x_0`, `x=5x_0`,…………`x=oo` on the x axis, and a charge `-q` is fixed at each of the points `x=2x_0`, `x=4x_0`, `x=6x_0`, …………`x=oo`. Here `x_0` is a positive constant. Take the electric potential at a point due to a charge Q at a distance r from it to be `Q//(4piepsilon_0r)`.Then, the potential at the origin due to the above system of
View SolutionA non-conducting ring of radius `0.5 m` carries a total charge of `1.11xx10^(-10)`C distributed non-uniformly on its circumference producing an electric field E everywhere is space. The value of the integral `int_(l=oo)^(l=0)-E.dI (l=0` being centre of the ring) in volt is
View SolutionSome equipotential surfaces are shown in figure .The electric filed strength is
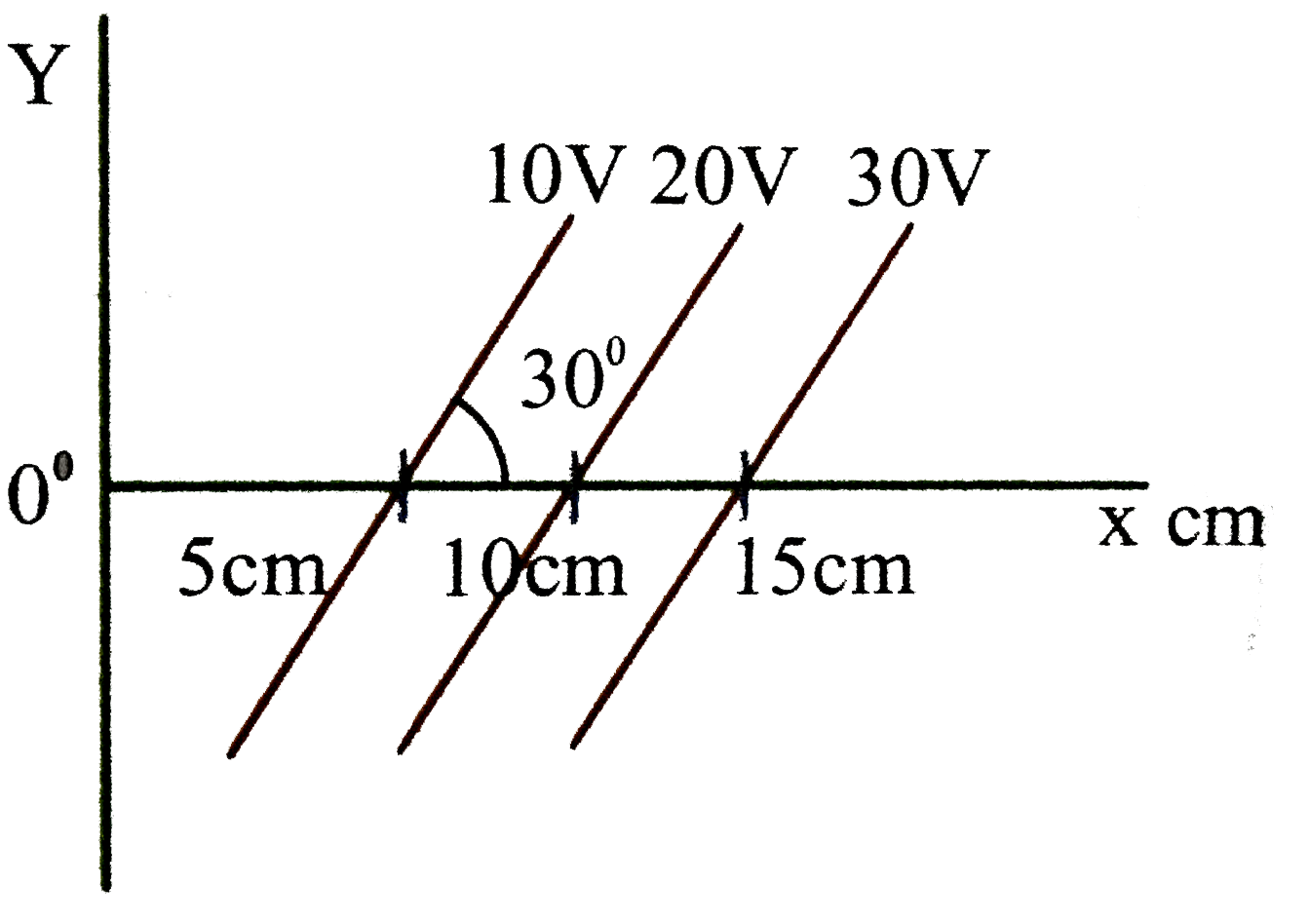
View SolutionHere is a special parallelogram with adajacent side length `2a` and `a` and the one of the possible angles between them as `60^(@)` .Two charges are to be kept across a diagonal only. The ratio of the minimum potential energyy of the system to the maximum potential energy is
View SolutionTwo concentric spherical conducting shells of radii R and 2R are carrying charges q and 2q, respectively. Both are now connected by a conducting wire. Find the change in electric potential (inV) on the outer shell.
View SolutionThe longer side of a rectangle is twice the length of its shorter side .A charge `q` is kept at one vertex.The maximum electric potential due to that charge at any other vertex is `V`, then the minimum electric potential at any other vertex will be
View SolutionThere are three unchanged identical metallic spheres `1,2 and 3` each of radius `r` and are placed at the verticles of an equlilateral triangle of side `d`.A charged metallic sphere having equal `q` of same radius `r` is touched to sphere `1` after some time it is taken to the location of sphere `2` and is touched to it ,then it is taken far away form sphere `1,2,3` after that the sphere `3` is grounded the charge on sphere `3` is (neglect electrostatic induction by assuming `d gt gt 2r)`
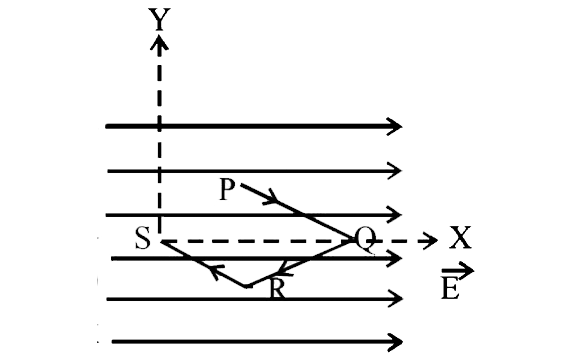
View SolutionA point charge q moves from point P to pont S along the path PQRS (fig.) in a uniform electric field E pointing parallel to the poistive direction of the X-axis. The coordinates of the points P, Q, R and S are(a, b, O), (2a, O, O)(a, -b,`ulO`) and `(O, O, O) respectively. The work done by the field in the above process is given by the expresison............
View SolutionThe potential at a point x ( measured in `mu` m) due to some charges situated on the x-axis is given by
`V(x)=20//(x^2-4) vol t`
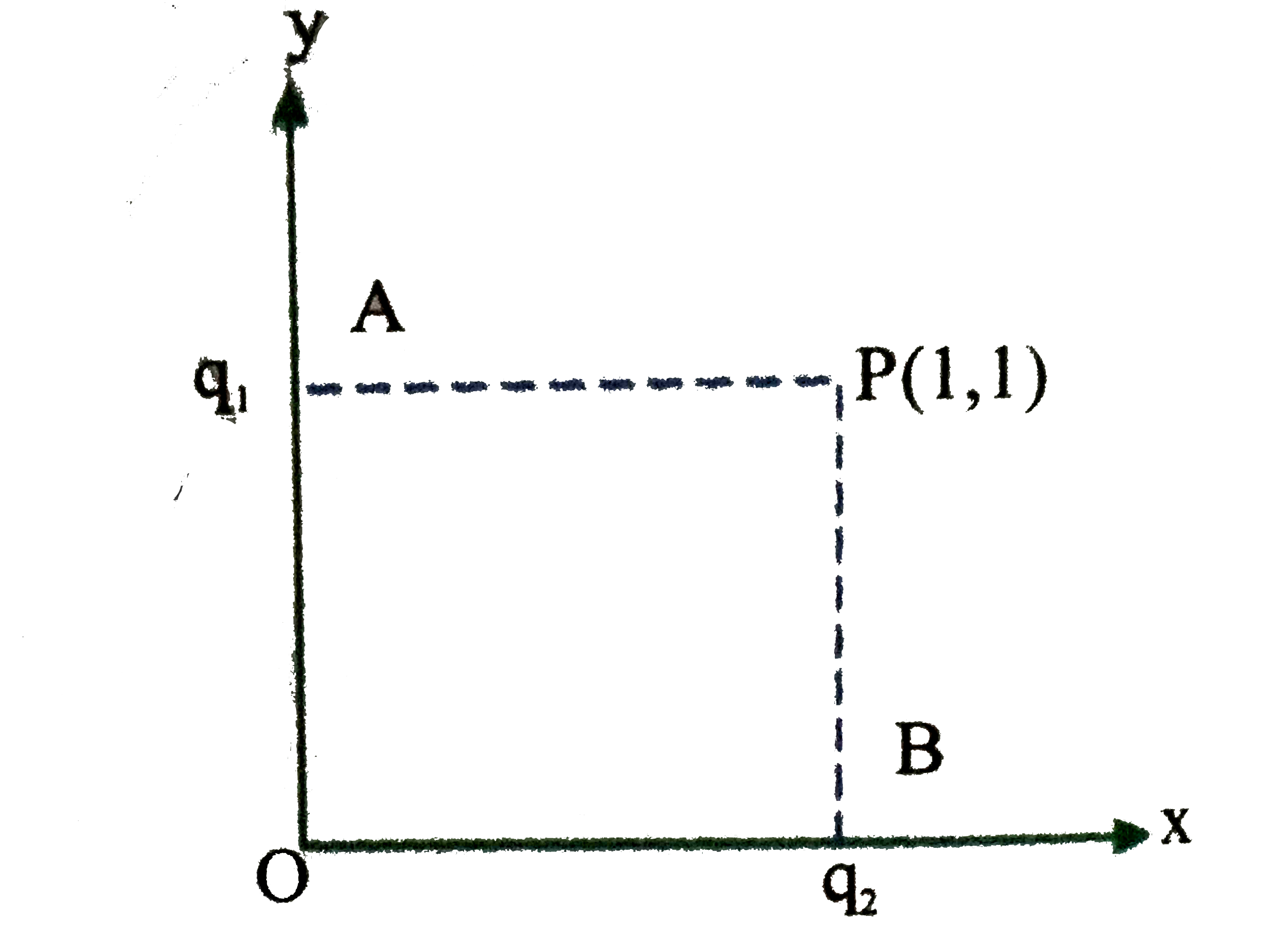
View SolutionTwo points charge `q_(1)` and `q_(2)(=q_(1)//2)` are placed at points `A(0,1)` and `B(1,0)` as shown in the figure.The electric field vector at point `P(1,1)` makes an angle `q` with the x-axis ,then the angle `q` is
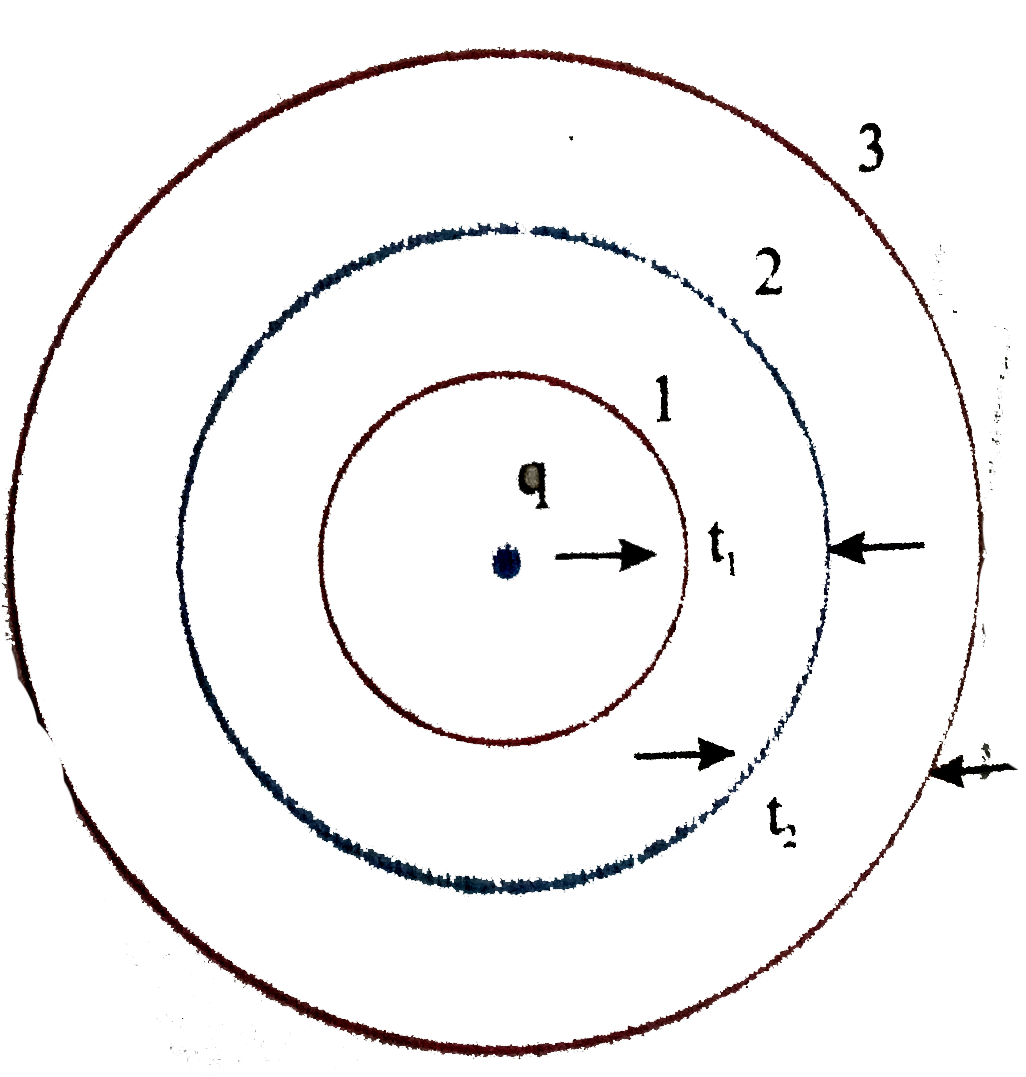
View SolutionFigures shows three spherical and equipotential surfaces `1,2` and `3` round a point charge `q`.The potential difference `v_(1)-v_(2)=V_(2)-V_(3)` if `t_(1)` and `t_(2)` be the distance between them ,then
View SolutionA half ring of radius `r` has a linear charge density `lambda`.The potential at the centre of the half ring is
View SolutionThe distance between plates of a parallel plate capacitor is `5d`. Let the positively charged plate is at `x=0` and negatively charged plate is at `x=5d`. Two slabs one fo conductor and other of a dielectric of equal thickness `d` are inserted between the plates as shown in figure. Potential verus distance graph will look like:

View SolutionA dielectric slab of thickness `d` is inserted in a parallel plate capacitor whose negative plate is at `x=0` and positive plate is at `x = 3d`. The slab is equidistant from the plates. The capacitor is given some charge. As one goes from `0` to `3d(1998)`.
View SolutionAn electron travelling from infinity with velocity `v` into an electric field to due to two stationsly electrons separated by a distance of `2m`.if it comes to rest when it reaches themid point of the line joinining the stationary electrons.The initial velocity `v` of the electron is
View SolutionWork performed when a point charge `2xx10^(-8)C` is transformed from intensity to a point at a distance of `1cm` form the surface charge density `sigma=10^(-8)C//cm^(2)`
View SolutionA conducting sphere `A` of radius `a` ,with charge `Q` , is placed concentrically inside a conducting shell `B` of radius `b` . `B` is earthed. `C` is the common centre of the `A` and `B`
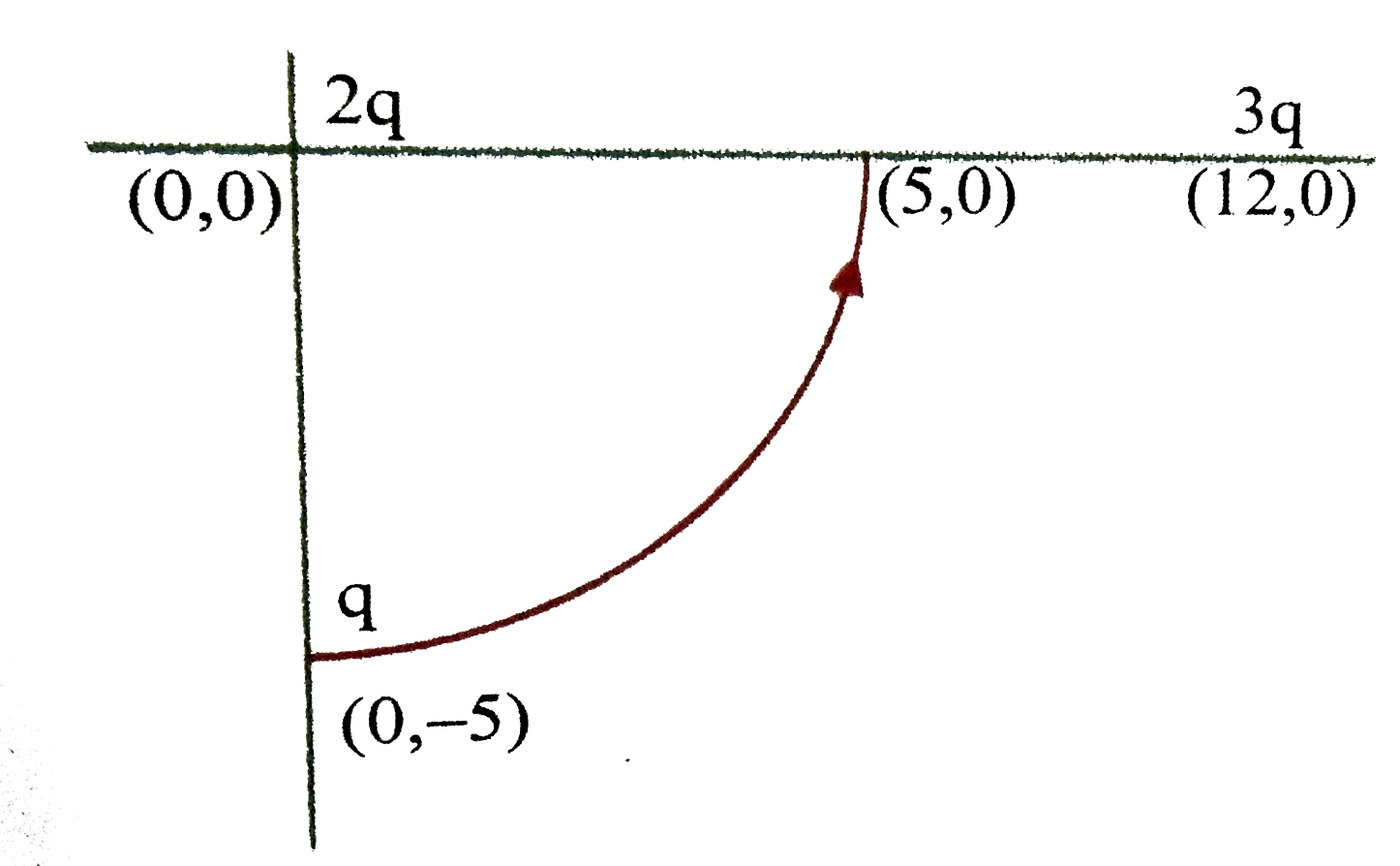
View Solution`2q` and `3q` are two charges separated by a distance `12cm` on x-axis .A third charge `q` is placed at `5cm` on `y-axis` as shown in figure .Find the change in potential energy of the system if `3q` is moved from initial position to a point on `X-axis` in circular path
View SolutionAn electron travelling from infinity with velocity `v` into an electric field due to two stationary electrons separated by a distance of `2m`.if it comes to rest when it reaches the mid point of the line joining the stationary electrons.The initial velocity `v` of the electron is
View SolutionA particle of mass an charge `q` is projected vertically upwards .A uniform electric field `vec(E)` is acted vertically downwards.The most appropiate graph between potential energy `U` (gravitaion plus eelectrostatic) and height h(lt lt radius of earth) is :(assume `U` to be zero on surface of earth)
View SolutionThe electric potential at a point `(x,0,0)` is given by `V=[(1000)/(x)+(1500)/(x)+(500)/(x^(3))]` "then the electric field at" `x=1` m is `(in volt//m)`
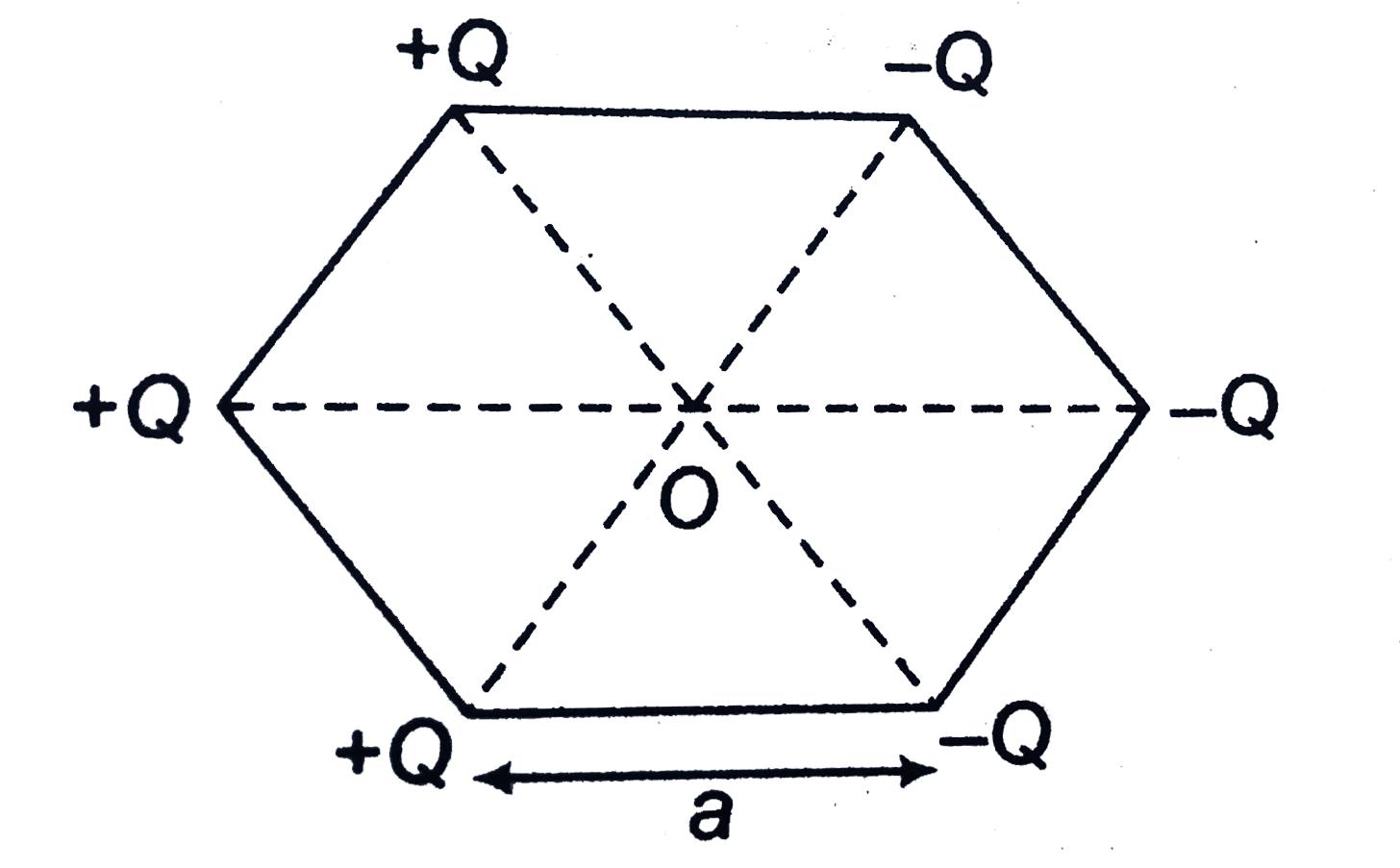
View SolutionSix charges are placed at the vertices of a rectangular hexagon as shown in the figure. The electric field on the line passing through point O and perpendicular to the plane of the figure as a function of distance x from point O is (xgtgta)
View SolutionA small electric dipole is placed at origin with its dipole moment directed along positive `x-axis` .The direction of electric field at point `(2,2sqrt(2),0)
View SolutionTwo electric dipoles each of dipolemoment `p=6.2xx10^(-30)C-m` are placed with their axis along the same line and their centres at a distanced =`10^(-8)cm`.The force of attraction between dipole is
View SolutionTwo point charges of `3.2 xx 10^-19 C and -3.2 xx 10^-19 C` are separated from each other by `2.4 xx 10^-10 m`. The dipole is situated in a uniform electric field of intensity `4 xx 10^5 Vm^-1`. Calculate the work done in roating the dipole by `180^(@)`.
View SolutionTwo opposite and equal chrages `4 xx 10^(-8)` coulomb when placed `2 xx 10^(-2) cm` away, from a dipole. If dipole is placed in an ecternal electric field `4 xx 10^(8)` newton//coulomb, the value of maximum torque and the work done in rotating it through `180^(@)` will be
View SolutionA point particle of mass M is attached to one end of a massless rigid non-conducting rod of length L. Another point particle of the same mass is attached to the other end of the rod. The two particles carry charges `+q` and `-q` respectively. This arrangement is held in a region of a uniform electric field E such that the rod makes a small angle `theta` (say of about 5 degree) with the field direction, fig. Find an expression for the minimum time needed for the rod to become parrallel to the field after it is set free.

View Solution
Level III (C.W) questions and complete solutions for chapter ELECTROSTATICS AND GAUSS LAW of NARAYANA PHYSICS (HINGLISH) of Class 12