Complete Solutions to Solved Example of chapter ELECTROSTATICS AND GAUSS LAW of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTROSTATICS AND GAUSS LAW |
| NARAYANA | Solved Example |
| Number Of Questions | 40 |
| Academic Year | 2023-24 |
Can two similarly charged bodies attract each other?
View SolutionTwo point sized identiacal sphere carrying charge `q_(1)` and `q_(2)` on them are separated by acertain distance the mutal force between them is `F` these two are brought in contant and kept at the same separation Now the force between them is `F^(1)` then .`(F^(1))/(F)=((q_(1)+q_(2))^(2))/(4q_(1)q_(2))`
View SolutionConsider three charges `q_(1),q_(2)` and `q_(3)` each equal to `q` at the verticles of an equilateral triangle of side `'l'` what is the force on any charge due to remianing charges.
View SolutionA particle of mass m carrying a charge `-q_(1)` starts moving around a fixed charge `+q_(2)` along a circular path of radius r. Find the time period of revolution T of charge `-q_(1)`.
View SolutionTwo identical small charged spheres, each having a mass m, hang in equilibrium as shown in fig. the length of each string is l, and the angle made by any string with the vertical is `theta`. Find the magnitude of the charge on each sphere.
View SolutionTwo identical balls each having a density `rho` are suspended from as common point by two insulating strings of equal length. Both the balls have equal mass and charge. In equilibrium each string makes an angle `theta` with vertical. Now, both the balls are immersed in a liquid. As a result the angle `theta` does not change. The density of the liquid is `sigma`. Find the dielectric constant of the liquid.
View SolutionA ring of radius `R` is with a uniformly distributed charge `Q` on it .A charge `q` is now placed in the centre of the ring .Find the increment in tension in the ring.
View SolutionA thin fixed ring of radius a has a positive charge q uniformly distributed over it.A particle of mass m having a negative charge Q, is placed on the axis at a distance of `x(xltlta)` form the center of the ring. Show that the motion of the negatively charged particle is approximately simple harmonic. Calculate the time period of oscillation.

View Solutiona point charge `q` is situated at a distance `r` from one end of a thin conduction rod of length `L` having a charge `Q` (unifromly distributed a long its length).find the magnitudes of electric froce between the two.
View SolutionTwo charge `+Q` each are placed at the two verticles of an equilateral triangle of side `a` .The intensity of electric field at the third vertex is
View SolutionTwo charge `+Q,-Q` are placed at the two verticels of an equilateral triangle of side `'a'`. Then the intensity of electric field at the third vertex is
View SolutionAn infinite number of charges each equal to q, are placed along the X-axis at `x = 1, x = 2, x = 4, x = 8`,…….. and so on.
(i) find the electric field at a point `x = 0` due to this set up of charges.
(ii) What will be the electric field if the above setup, the consecutive charges have opposite signs.
View SolutionA point mass `m` and charge `q` is connected with a spring of negligible mass with natural length `L`., Initially spring is in natural length .Now a horizontal unifrom electric field `E` is switched on as shown .Find (a) The maximum separation between the mass and the well
(b) Find the separation of the point mass and wall at the equilbrium position of mass
(c ) Find the energy stored in the spring at the equilirbium position of the point mass
`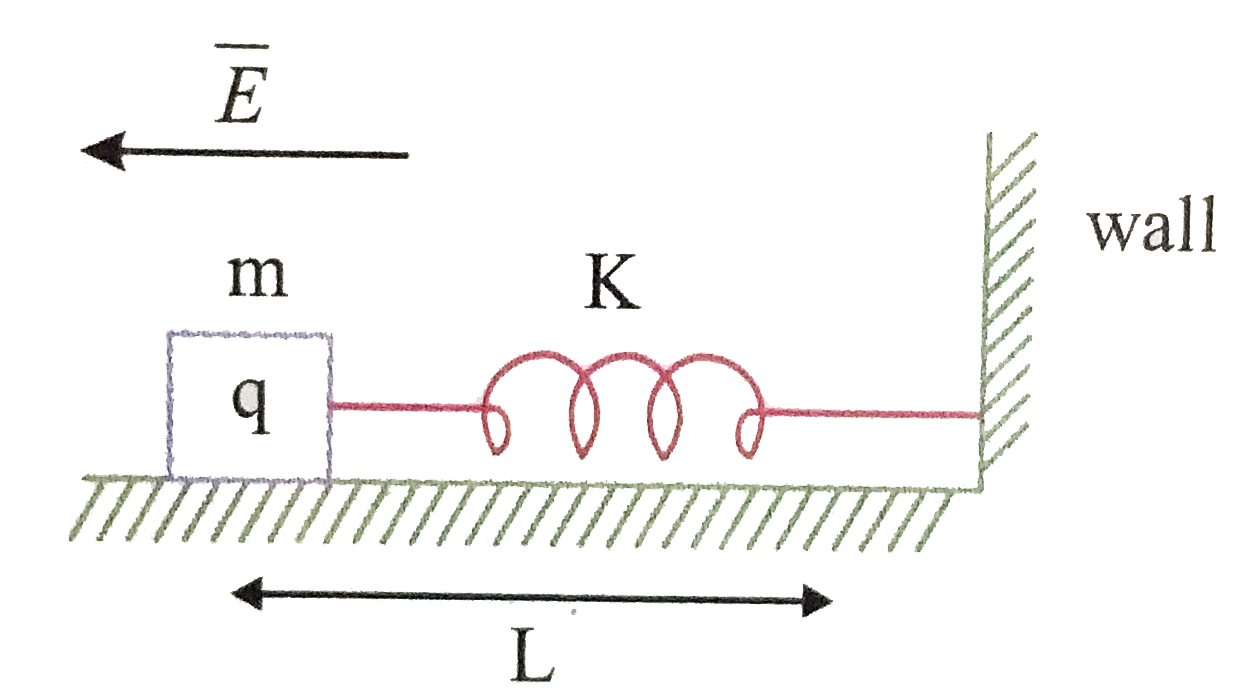
View SolutionA block having mass `'m'` ad carge `q` is resting on a fractionless plane at distance `L` from the wall as shown in fig.Discuss the motion of the block when a uniform electric field `E` is applied horizontally towards the wall assuming that collision of the block with the wall is perfectly elastic.
View SolutionSix charges are placed at the vertices of a rectangular hexagon as shown in the figure. The electric field on the line passing through point O and perpendicular to the plane of the figure as a function of distance x from point O is (xgtgta)
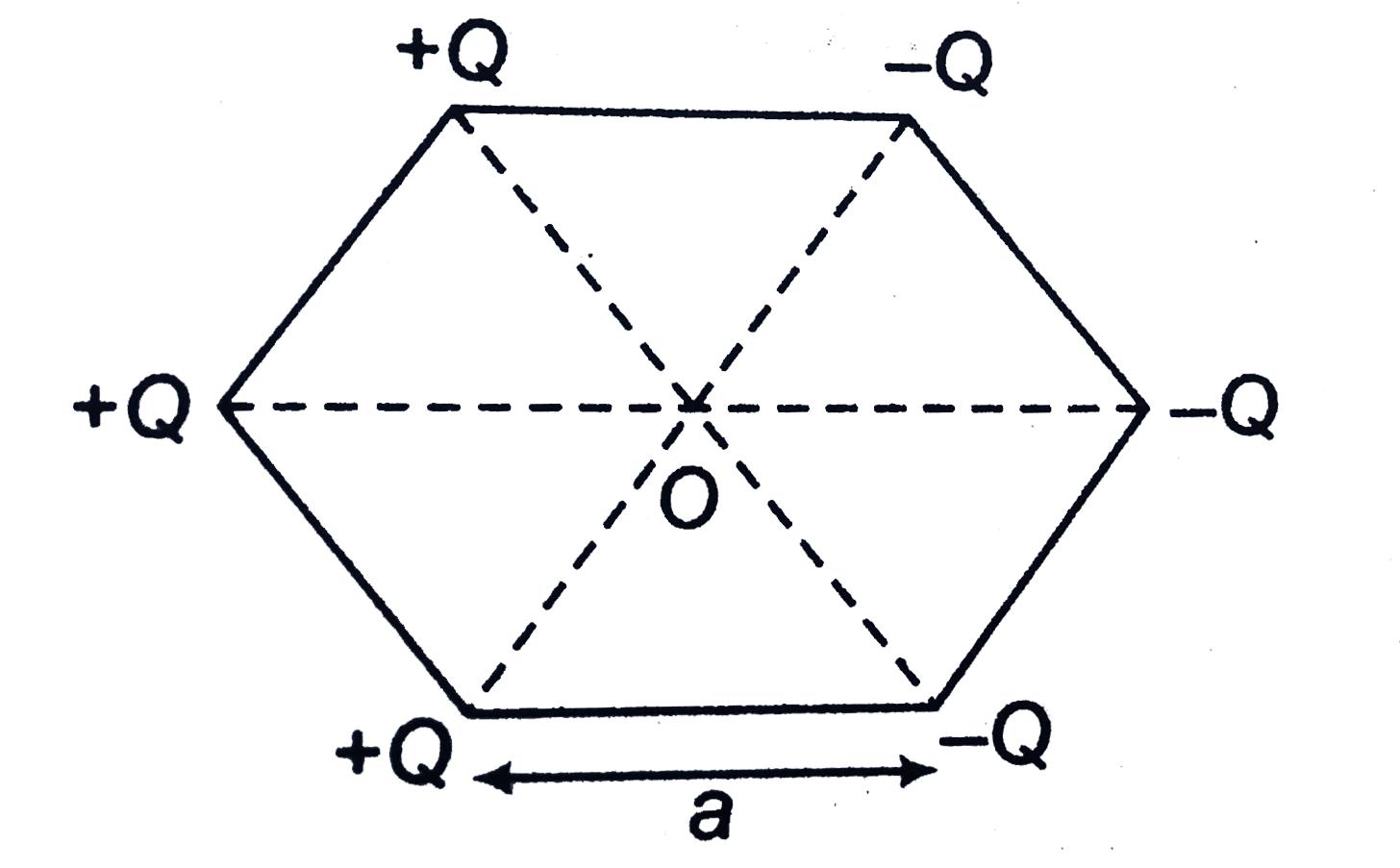
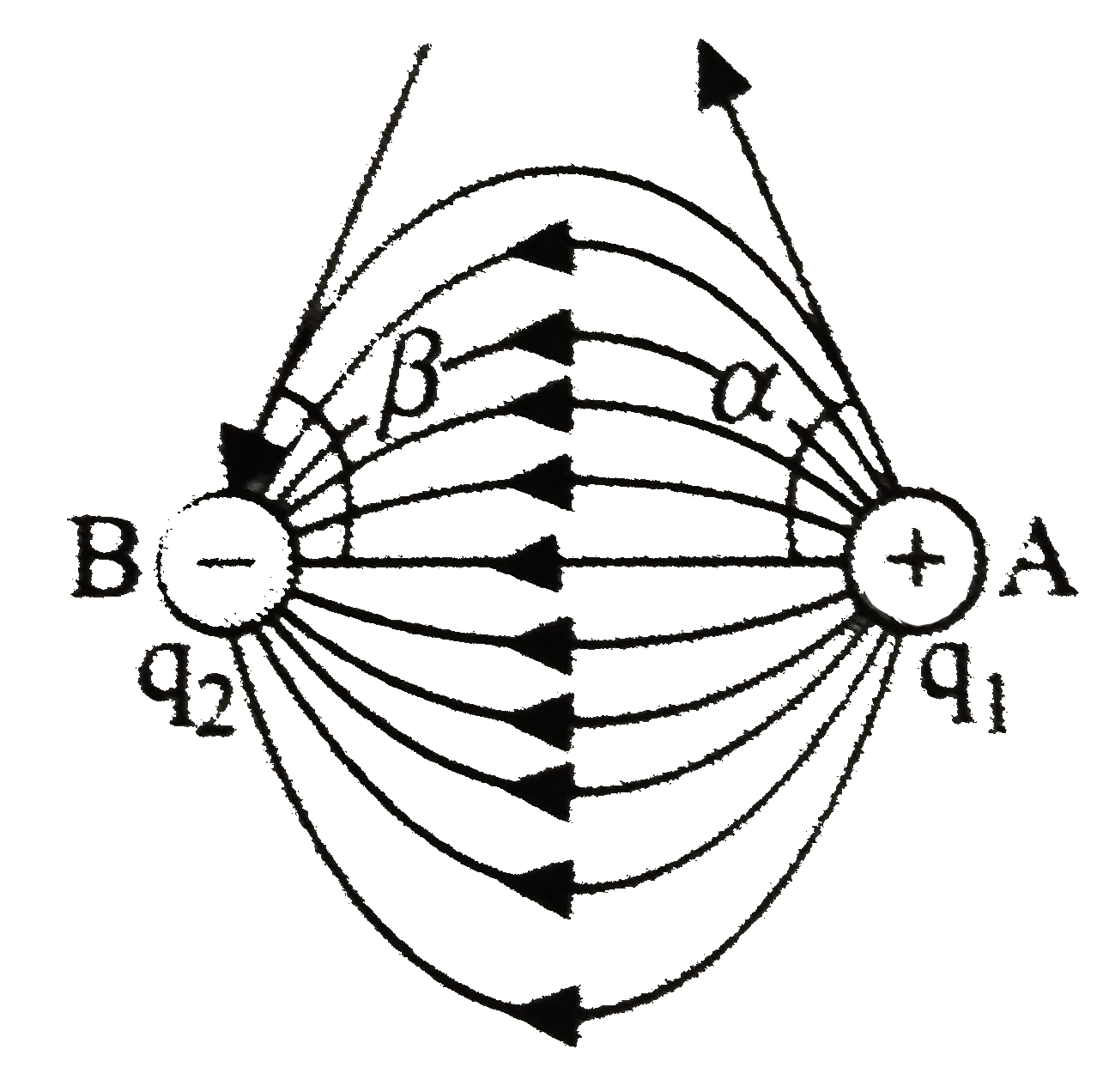
View SolutionThe field lines for two point charges shown in fig.

(i) Is the field uniform?
(ii) Determine the ratio `q_(A)//q_(B)`.
(iii) What are the sign of `q_(A)` and `q_(B)` ?
(iv) Apart from infinity, where is the neutral point?
(v) If `q_(A)` and `q_(B)`are separated by a distance `10(sqrt(2)-1)` cm, find the position of neutral point.
(vi) where will the lines meet which are coming from A and are not meeting at `q_(B)`?
(vii) Will a positive charge follow the line of force if free to move?
View SolutionConsider a circular arc of radius `R` which subtends an angle `phi` at its centre .Let us calculate the electric field strength at `C`
View SolutionAn electric dipole of moment `p` is kept at a distance `r` form an infinte long charged wire of linear charge density `lambda` as shown.Find the force acting on the dipole?

View SolutionA charge 'Q' is distributed over two concentric hollow spheres of radii 'r' and 'R' (gtr) such that the surface densities are equal. Find the potential at the common centre.
View SolutionThe electric potential V at any point x, y, z (all in meters) in space is given by `V=4x^2` volts. The electric field at the point (1m, 0, 2m) is……………..`V//m`.
View SolutionA conducting liquid bubble of radius a and thickness ` t ( tltlt a)` is charged to potential `V`. If the bubble collapses to a droplet , find the potential on the droplet .
View SolutionCharge `q_(1)` is fixed and another point charge `q_(2)` is placed at a distance `r_(0)` form `q_(1)` on a frictionless horizontal surface.Find the velocity of `q_(2)` as a function of seperation `r` between them (treat the changes as point charges and mass of `q_(2)` is m)
View SolutionA proton moves with a speed of `7.45x10^(5)m//s` directly towards a free proton orginally at rest.Find the distance of closest approach for the two protons. Given `(1//4pi epsilon_(0)_=9xx10^(9)m//s,m_(p)=1.67xx10^(-27)kg` and `e=1.6xx10^(-19)`coulomb.
View SolutionA small ball if mass `2 xx 10^(-3) Kg` having a charges of ` 1 mu C` is suspended by a string of length ` 0. 8 m` Another identical ball having the same charge is kept at the point of suspension . Determine the minimum horizontal velocity which should be imparted to the lower ball so that it can make complete revolution .
View SolutionIF an electorn enters into a space between the plates of a parallel plate capacitor at an an angle `alpha` with the plates an leaves at an angle `beta` to the plates find the ratio of its kinetic energy while entering the capacitor of that while leaving.
View Solution(Figure 3.51) shows two concentric conducting shells of radii `r_(1)` and `r_(2)` carrying uniformaly distributed charges `q_(1)` and `q_(2)`, respectively. Find an expression for the poptential of each the potential of each shell.
 .
.
View SolutionIn (Fig. 3.73), if the inner shell has charge `+q_0` and the outer shell is earthed, then
 .
.
i. determine the charge on the outer shell, and
ii. find the potential of the inner shell.
View SolutionConsider two concentric spherical metal shells of radii `'a'` and `bgt a` .The outer shell has charge `Q` but the inner shell has no charge.Now the inner shell is grounded ,This means that the inner shell will come at zero potential and that electric fields lines leave the outer shell and end on the inner shell.(a) Find the charge on the inner shell
Find the potential on outer sphere.

View SolutionTwo circular loops of radii `0.05` and `0.09 m`, respectively, are put such that their axes coincide and their centers are `0.12 m` apart. A charge of `10^-6 C` is spread uniformly on each loop. Find the potential difference between the centers of the loops (in kV).
View SolutionA circular ring of radius R with uniform positive charge density `lambda` per unit length is located in the y z plane with its center at the origin O. A particle of mass m and positive charge q is projected from that point `p( - sqrt(3) R, 0,0)` on the negative x - axis directly toward O, with initial speed V. Find the smallest (nonzero) value of the speed such that the particle does not return to P ?
View SolutionA particle that carries a charge `-q` is placed at rest in uniform electric field `10N//C` .It experiences a force and moves .In a certain time 't' it is observed to acquire a velocity `10bar(i)-10bar(i)m//s` The given electric field intersects a surface of area `1m^(2)` in the `x-z` plane .Find the Electric flux through the surface.
View SolutionThe electric fields in a region is given by `vec(E)=E_(0)(x)/(L)hat(i)` ,Find the charge contained inside a cubical volume bounded by the surface `x=0,x=L,y=0,y=L,z=0,z=L`.
View SolutionA square surface of side `L m` is in the plane of the paper. A uniform electric field `vec(E )(V//m)`, also in the plane of the paper, is limited only to the lower half of the square surface (see figure). The electric flux in `SI` units associated with the surface is:

View SolutionA hollow cylinder has a charge `qC` within it. If `phi` is the electric flux in unit of voltmeter associated with the curved surface `B` the flux linked with the plance surface `A` in unit of voltmeter will be

View SolutionThe adjacent diagram shows a charge `+Q` held on an insulating support `S` and enclosed by a hollow spherical conductor,`O` represent the center of the spherical conductors and `P` is a point such that `OP=x` and `SP=r` .The electric field at point `P` will be

View SolutionThe electrostatic potential inside a charged spherical ball is given by `phi = ar^(2) + b`, where r is distance from the center of the ball, a and b are constants. Calculate the charge density inside the ball.
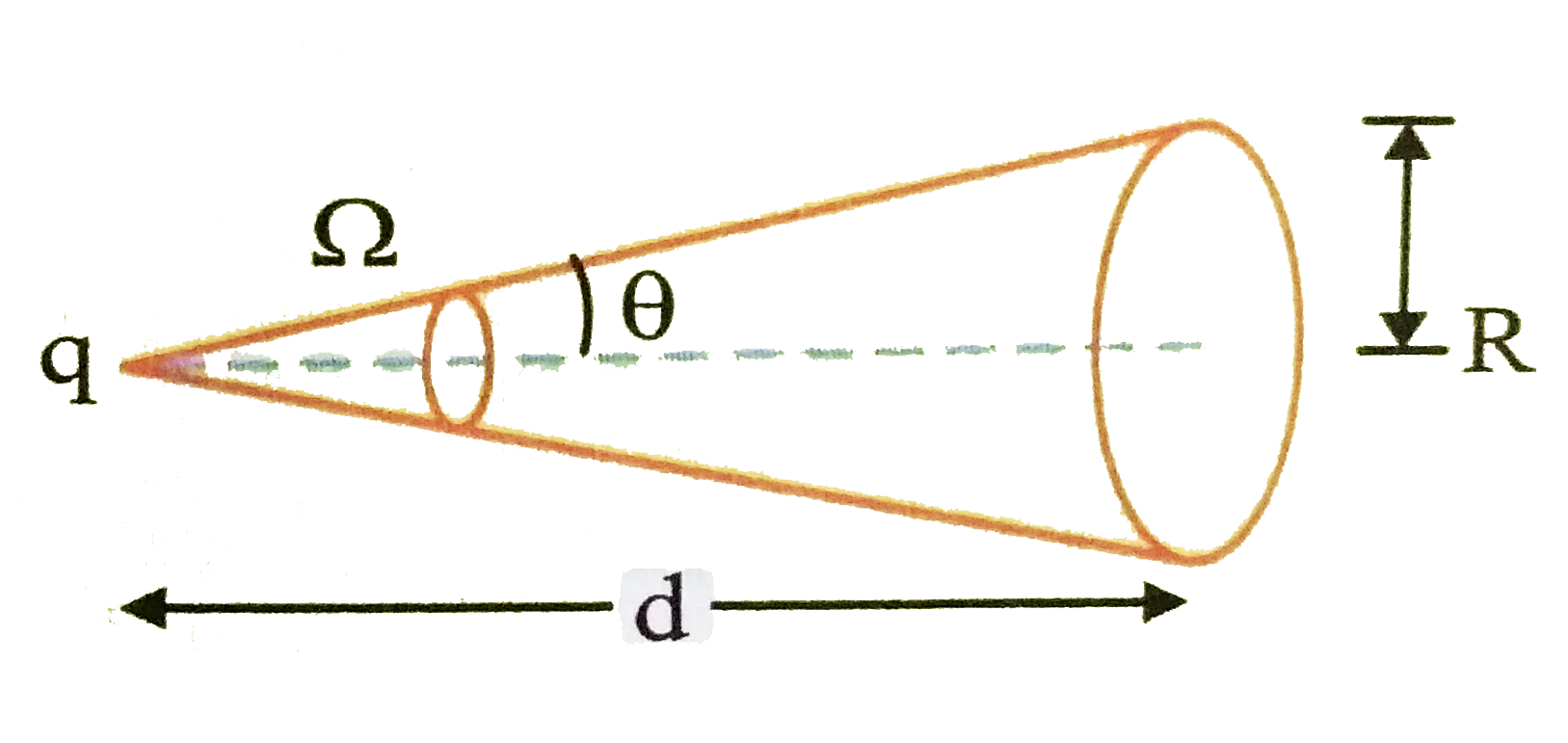
View SolutionA point charge `q` is placed at a distance `d` form the center of circular disc of radius `R`. Find electric flux through the disc due to that charge
View SolutionTwo charges`+q_(1)` and `-q_(2)` are placed at A and B respectively. A line of force emanates from `q_(1)` at an angle `alpha` with the line AB. At what angle will it terminate at `-q_(2)` ?
View SolutionA thin spherical shell radius of `R` has of charge `Q` unfromily distributed on it.At the centre of the shell ,a negative point charge `-q` is placed.IF the shell is cut into two identical hemisphere still equlibrium is maintained .Then find the relation between `Q` and `q`?
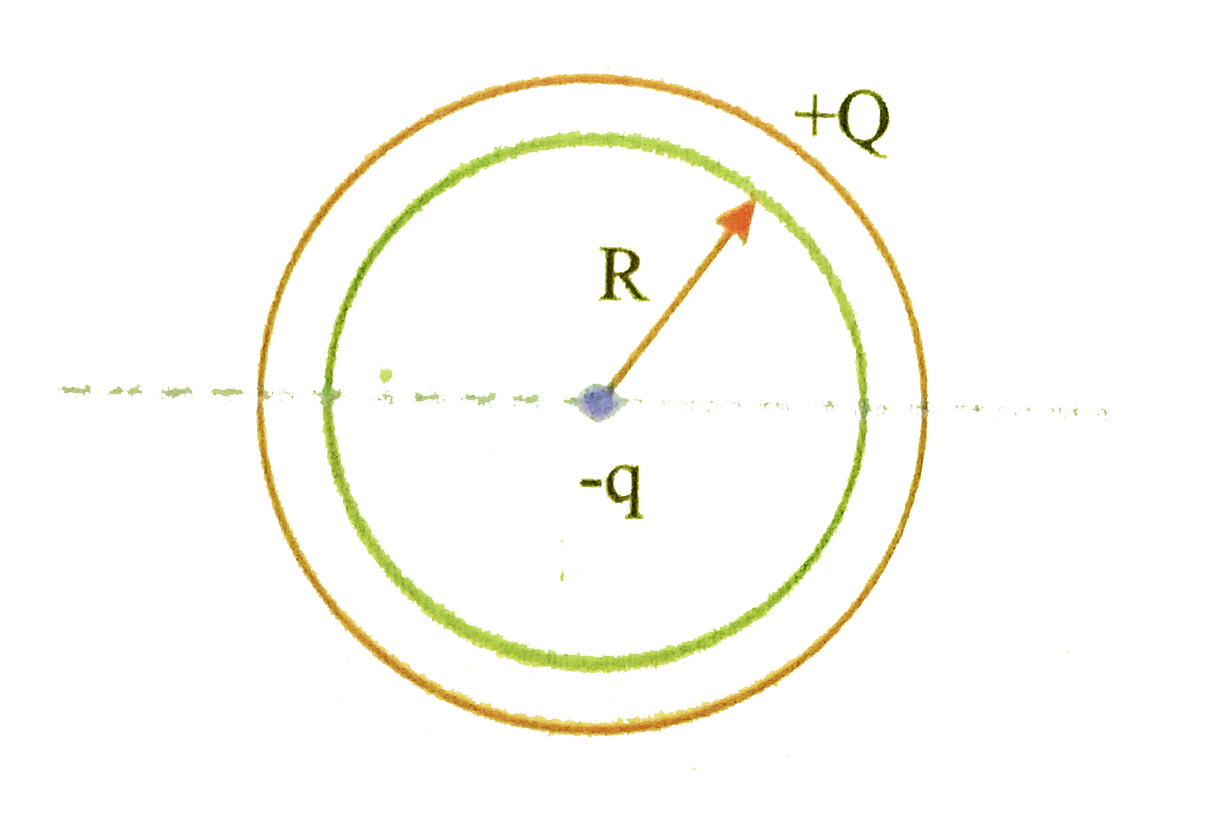
View SolutionIf `r` and `T` are radius and surface tension of a spherical soap bubble respectively then find the charge needed to double the radius of bubble.
View Solution
Solved Example questions and complete solutions for chapter ELECTROSTATICS AND GAUSS LAW of NARAYANA PHYSICS (HINGLISH) of Class 12