Complete Solutions to Level V of chapter ELECTROSTATICS AND GAUSS LAW of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTROSTATICS AND GAUSS LAW |
| NARAYANA | Level V |
| Number Of Questions | 93 |
| Academic Year | 2023-24 |
the linear charge density of a thin metallic rod varies with the distance `x` from the end as `lambda=lambda_(0)x^(2)(0 le x lel)` The total charge on the rod is
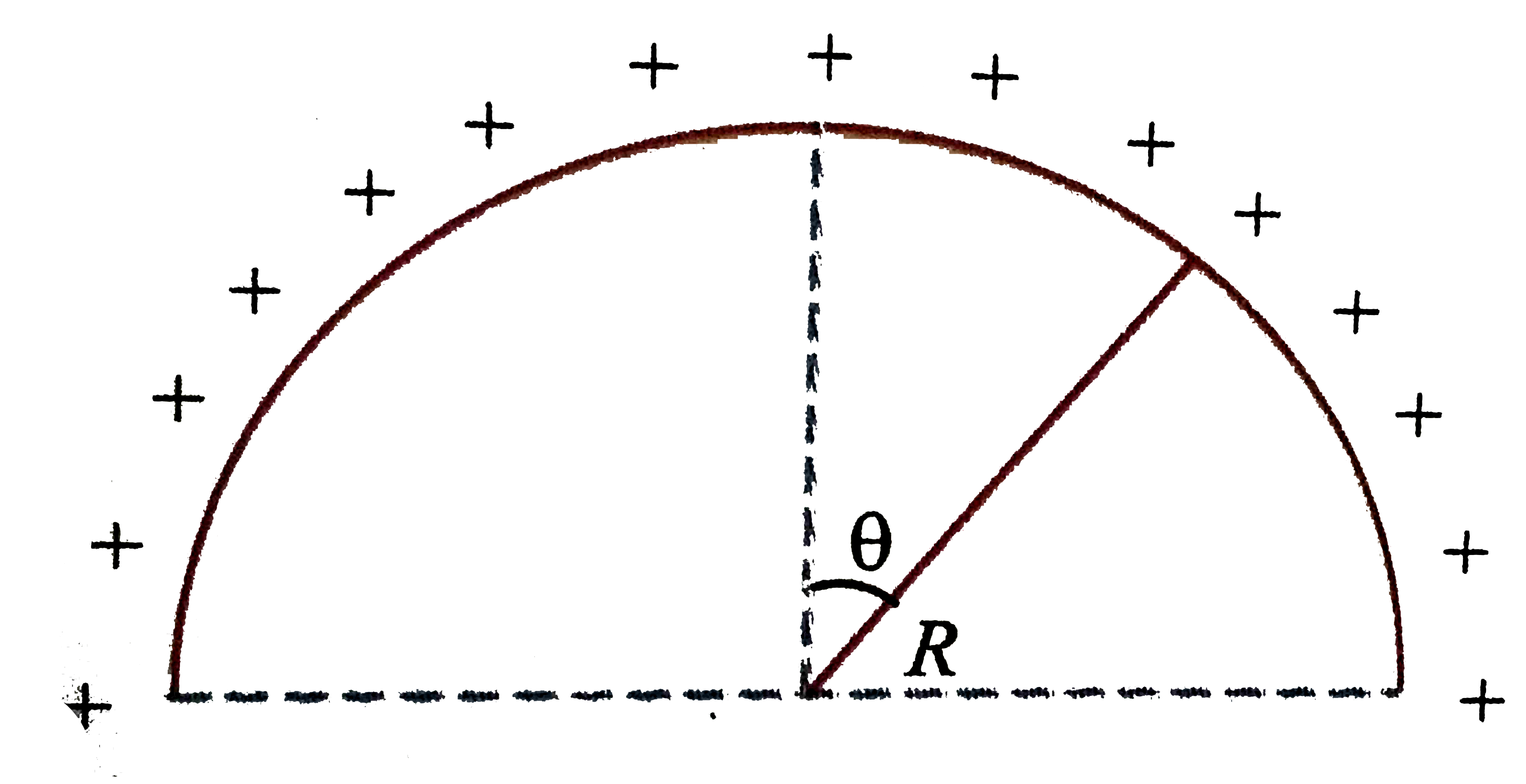
View SolutionThe linear charge density of a uniform semicircular wire varies with `theta` shown in the figure as `lambda=lambda_(0)costheta` if `R` is the radius of the loop ,of the charge on the wire is
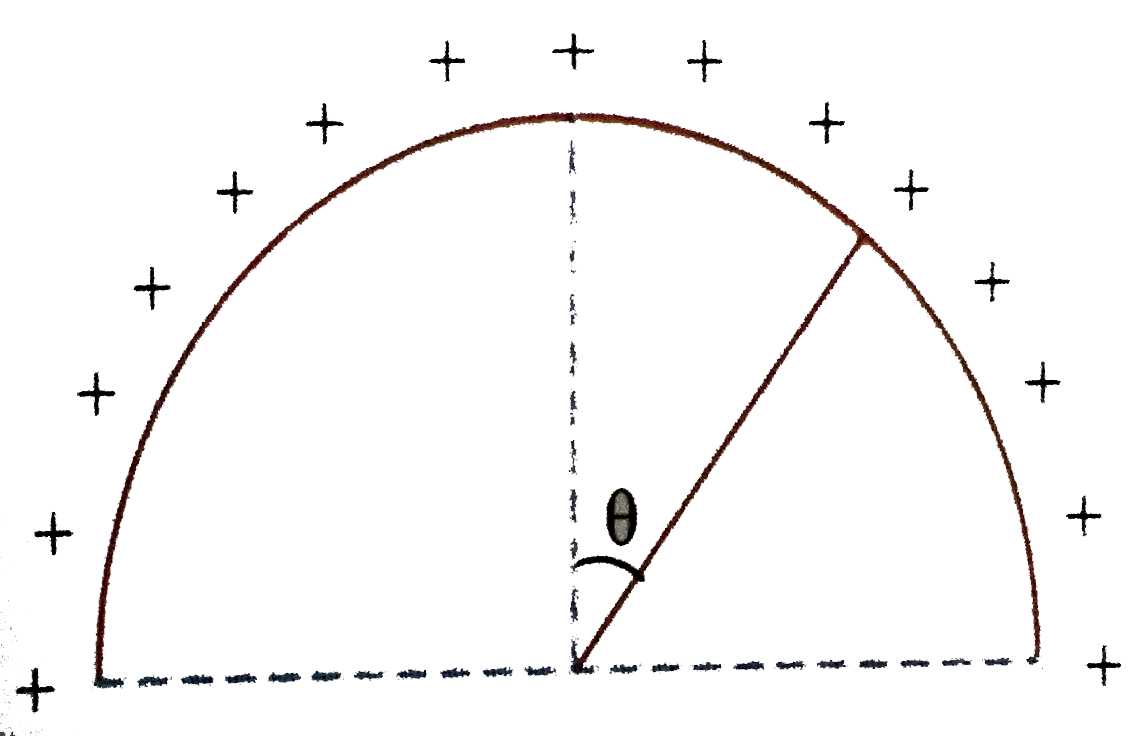
View SolutionFor the hemisphere of radius `R` shown in the figure the surface charge density `sigma` varies with `theta` (shown in figure) as `sigma=sigma_(0) costheta` the total charge on the sphere is
View SolutionA charge `+Q` is uniformly distributed along the circular arc of radius `R` as shown in the figure.The magnitude of the force experienced by the point charge `+q` place at the centre of curvature is `(k=(1)/(4piepsilon_(0)))`

View SolutionA ring of radius `R` is with a uniformly distributed charge `Q` on it .A charge `q` is now placed in the centre of the ring .Find the increment in tension in the ring.
View SolutionTwo metallic spehres each of mass `M` and radius `R` charged separately to `Q_(1)` and `Q_(2)` are at a distance `d` between their centres `(d gt2R)` The force between them will be
View SolutionA positive point charge `+Q` is fixed in space .A negative point charge `-q` of mass `m` revolves around a fixed charge in elliptical orbits .The fixed charge `+Q `is at one focus of the ellipse.The only force acting on negative charge is the electrostatic force due to positive charge is the electrostatic force due ot positive charge.Then which of the following statement is true

View SolutionFind the force experienced by a semicircular rod having a charge q as shown in fig. Radius of the wire is R, and the line of charge with linear charge density `lambda` passes through its center and is perpendicular to the plane of wire.
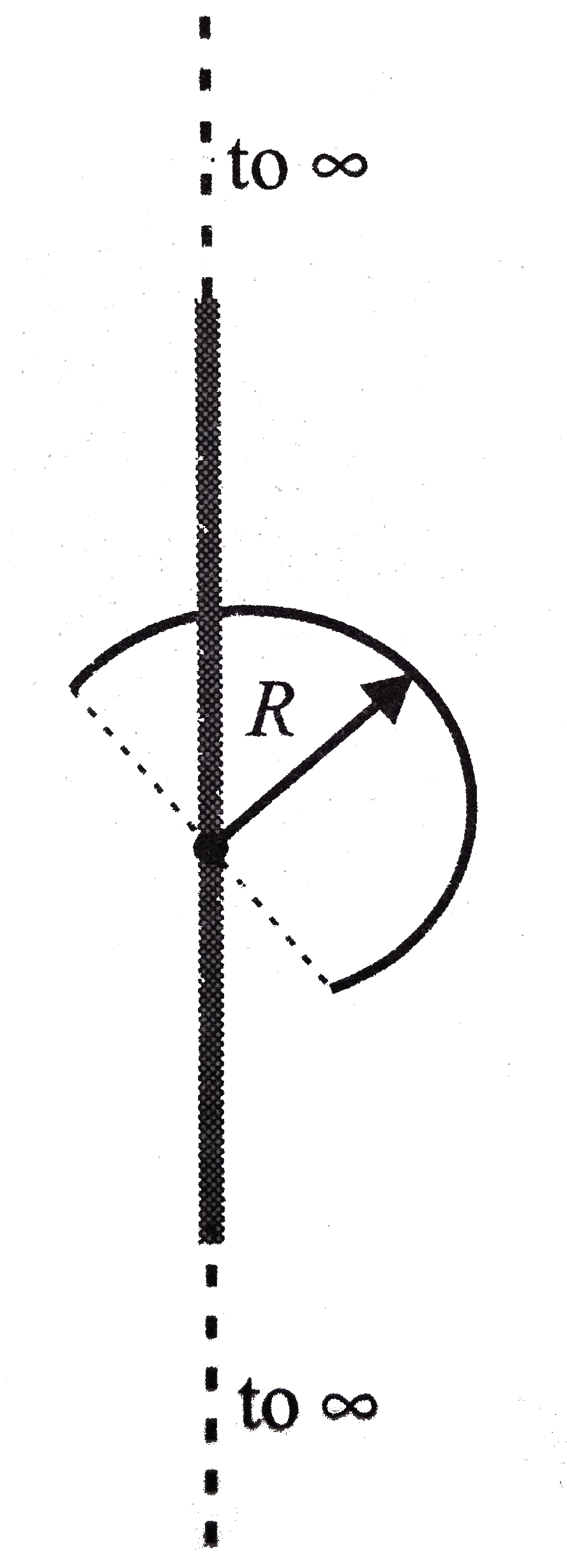
View SolutionTwo infinitely large charged planes having uniform suface charge density `+sigma` and `-sigma` are placed along `x-y` plane and `yz` plane respectively as shown in the figure. Then the nature of electric lines of forces in `x-z` plane is given by:

View SolutionA conducting liquid bubble of radius a and thickness ` t ( tltlt a)` is charged to potential `V`. If the bubble collapses to a droplet , find the potential on the droplet .
View SolutionA uniform electric field of magnitude `325 Vm^-1` is directed in the negative y - direction in (fig. 3.12). Theb coordinates of point A are `(-0.2 m , -0.3 m)` and those of point B are `(0.4 m, 0.5 m)`. Calculate the potential difference `V_B - V_A` along the path shown in the figure.
 .
.
View SolutionAn infintie by long plate has surface change density `sigma` As shown in the fig .apoint charge `q` is moved form `A` to `B` .Net work done by electric field is
View Solutiona conducting disc of radius `R` roatates about its axis when an angular velocity `omega`.Then the potential difference between the centre of the disc and its edge is (no magnetic field is present ):
View SolutionA neutral conducting spherical shell is kept near a charge `q` as shown .The potentilal at point `P` due to the induced charge is
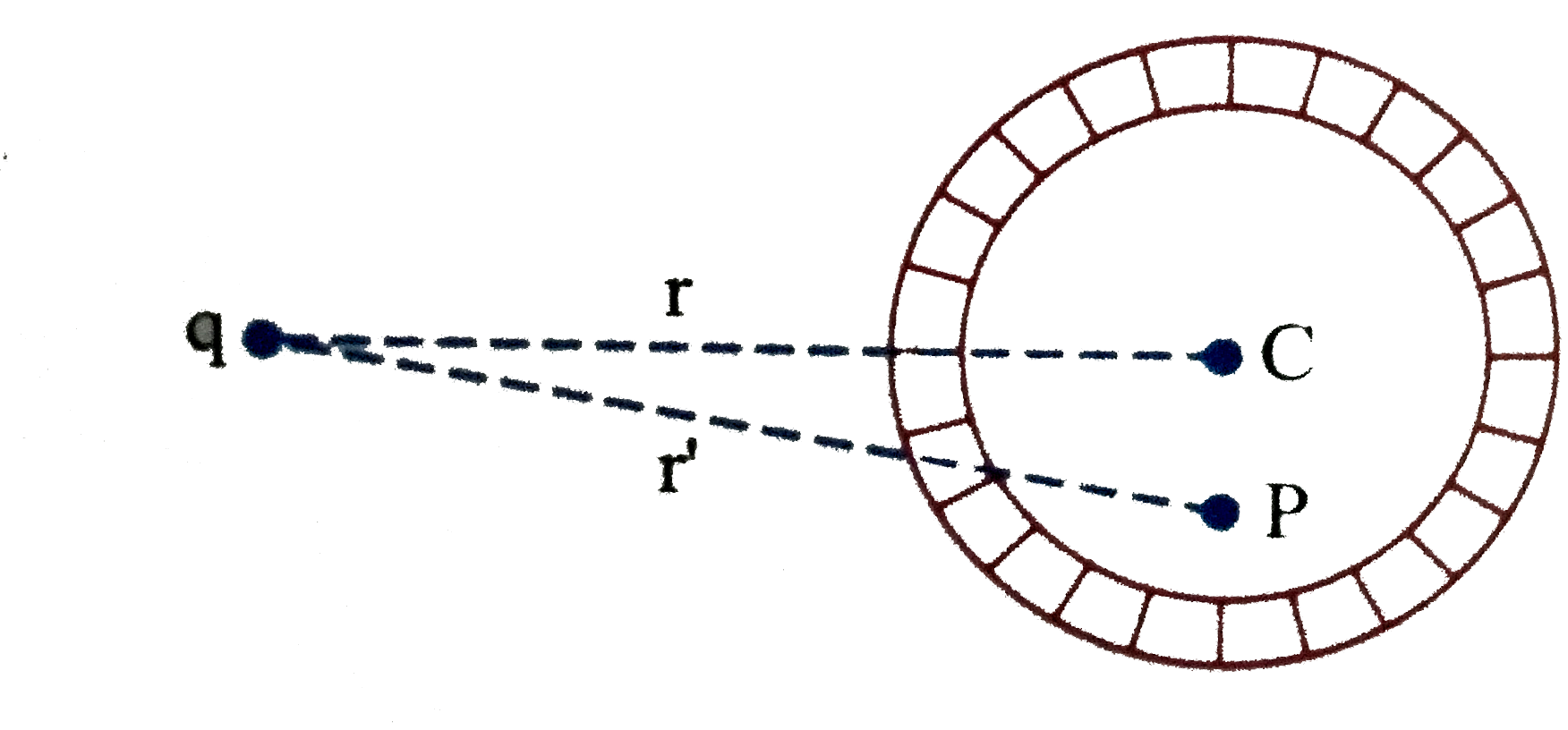
View Solutionthe following diagram represents a semi circular wire of linear charge density `lambda=lambda_(0)sin theta` where `lambda_(0) `is a positive constant.The electric potential at `o` is (take `k=(1)/(4piepsilon_(0))`
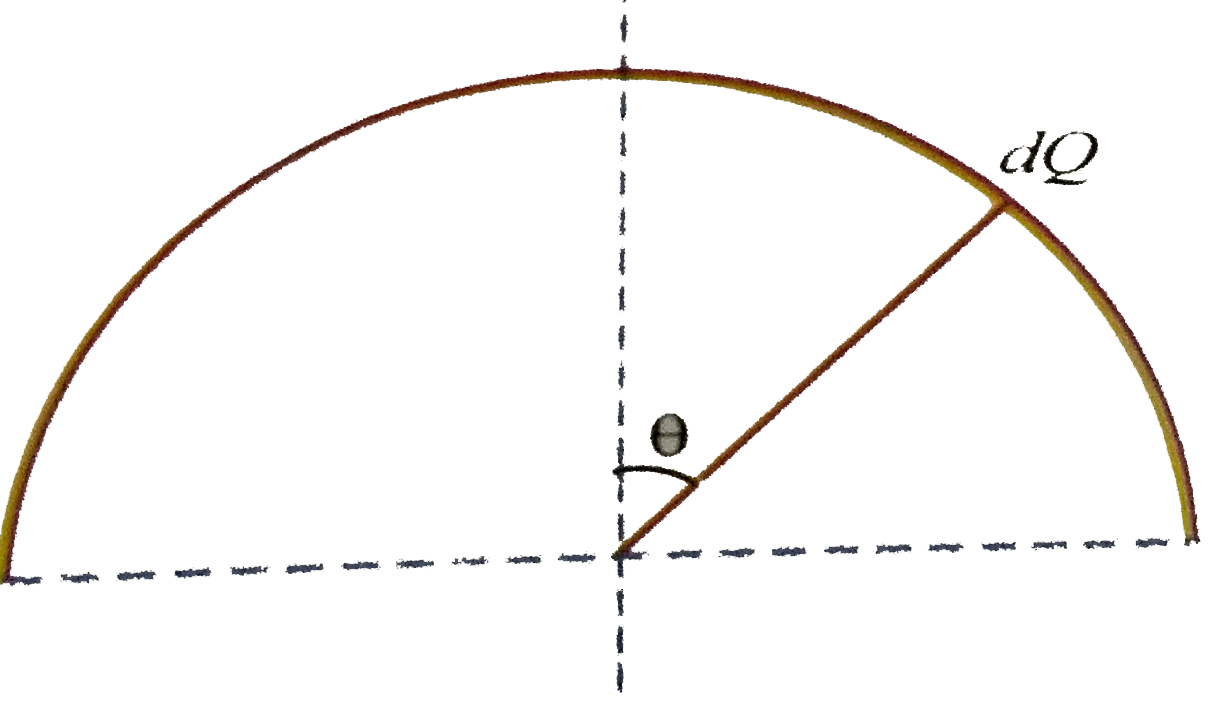
View SolutionFind the electric field potentail and strength at the centre of a hemisphere fo raidus `R` ahcged uniformly with the the surface density `sigma`.
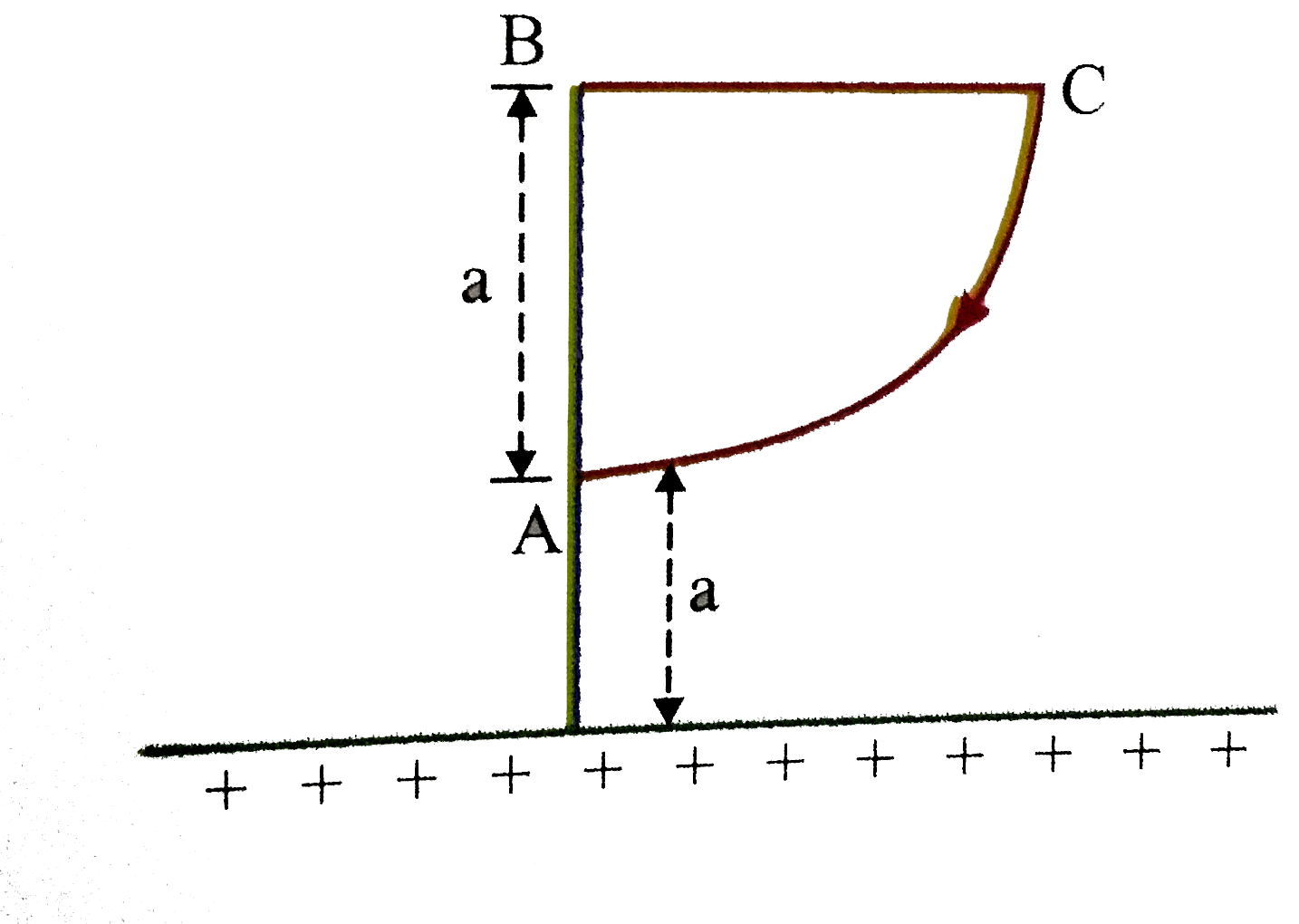
View SolutionFor an infinite line of charge having linear charge density `lambda` lying along x-axis the work done in moving a charge `q` form `C` to `A` along `CA` is
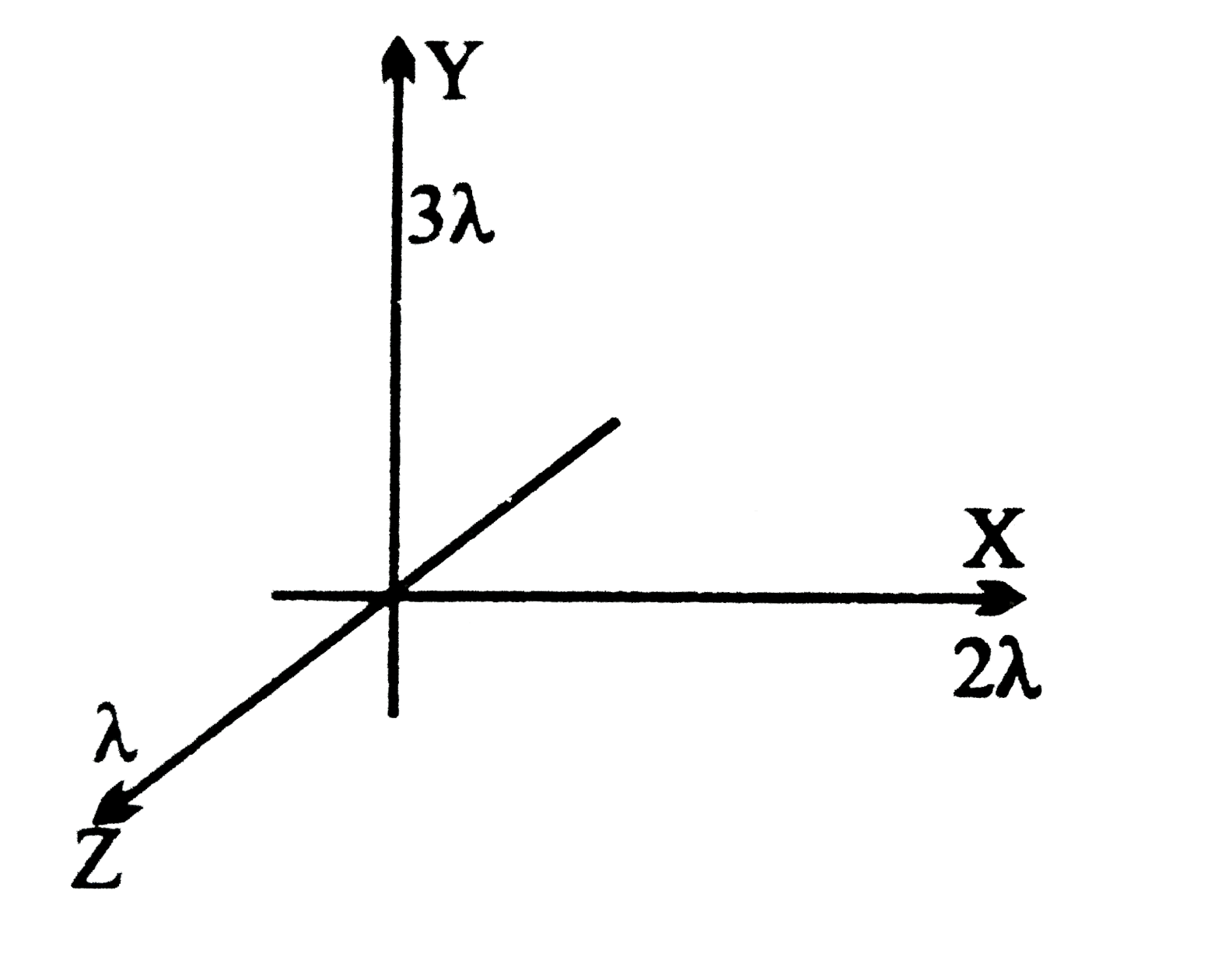
View SolutionThe diagram shows three infinitely long uniform line charges placed on the `X, Y` and ` Z` axis . The work done in moving a unit positive charge from (1,1,1) to (2 , 1,1,) is equal to
 .
.
View SolutionTwo positively charged particles ` X` and `Y` are initially far away from each other and at rest , `X` begins to move towards `Y` with some initial velocity. The total momentum and energy of the system are `p` and `E`.
View SolutionA metal ball of radius `R` is placed concentrically inside hollow metal sphere of inner radius `2R` and outer radius `3R`.The ball is given a charge `+2Q` and the hollow sphere a total charge `-Q` .The electrostatic potential energy of this system is
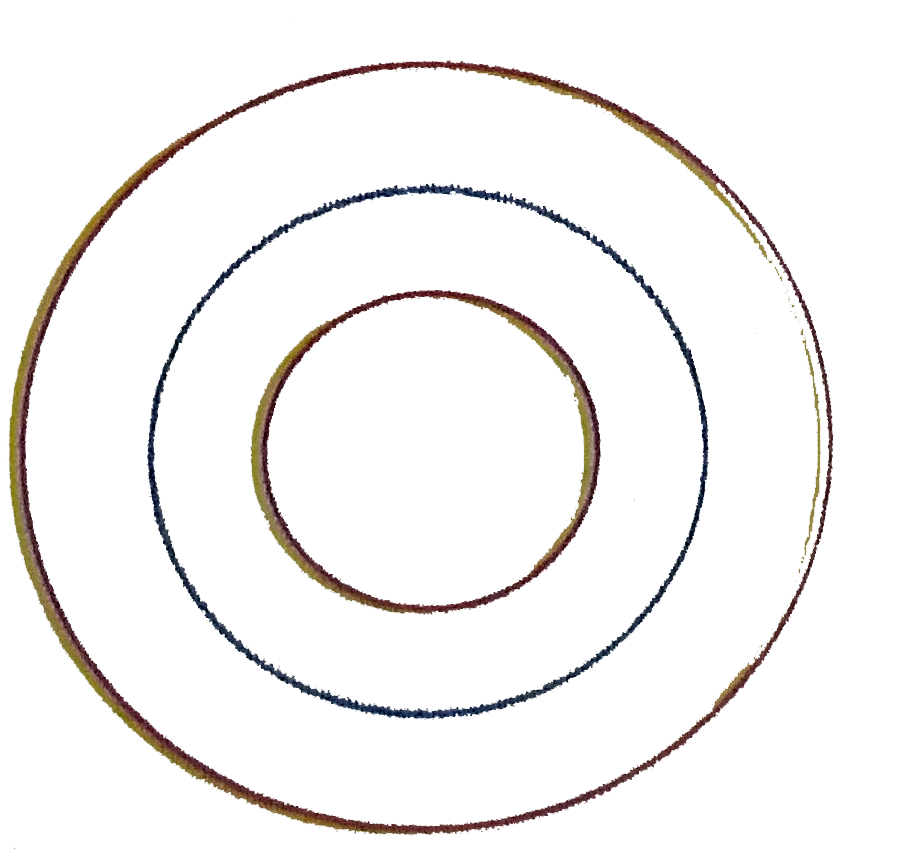
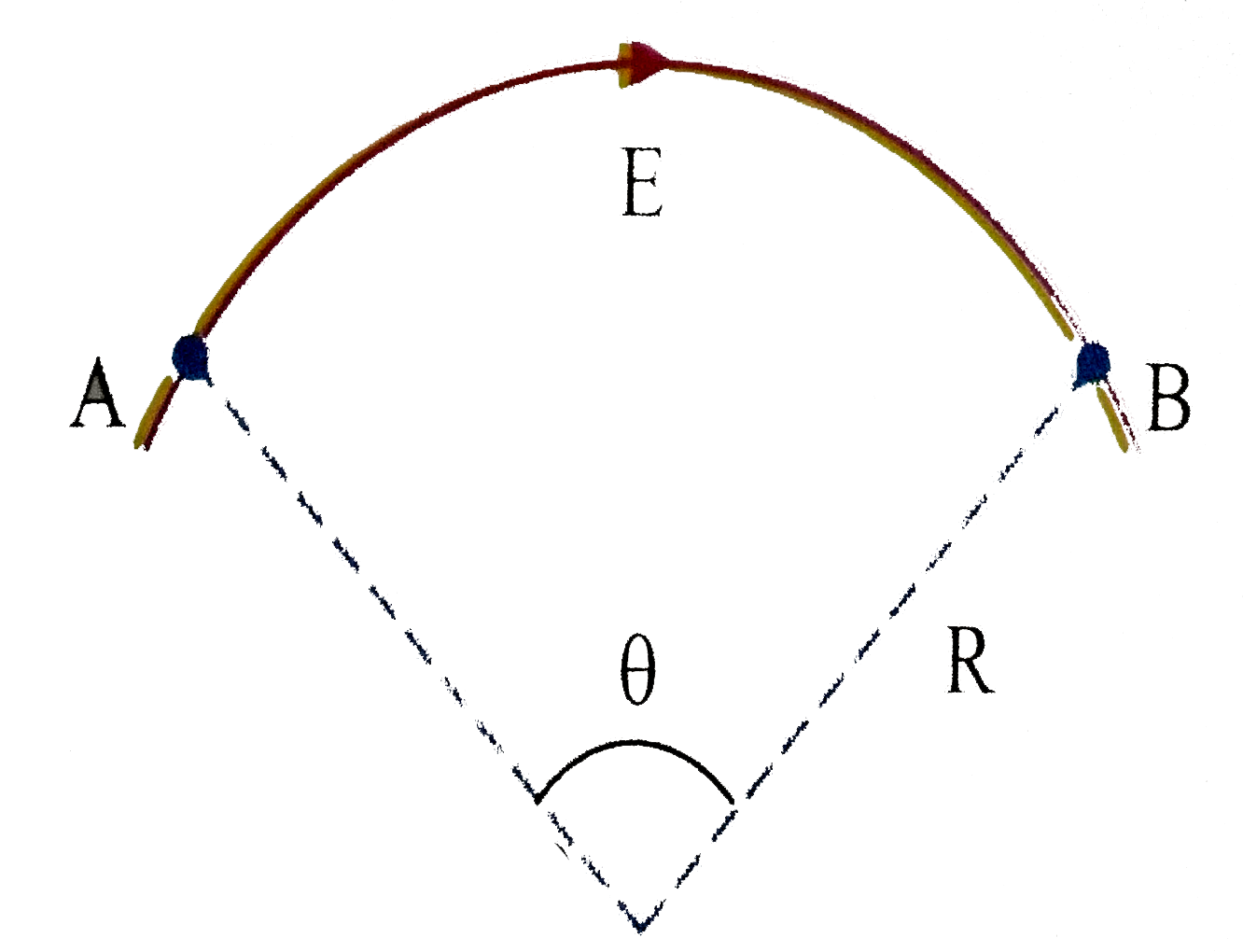
View SolutionFigures shows an electric line of force which curves along a circular arc.The magnitude of electric field intensities is same at all points on this curve and is equal to `E`.If the potential at `A` is `V` ,the potential at `B` is
View SolutionUniform electric field of magnitude `100 Vm^-1` in space is directed along the line `y = 3 + x`. Find the potential difference between points `A (3,1) and B (1,3)`.
View SolutionElectrical potential `V in space as a function of `co-ordinates is given by `,V=(1)/(x)+(1)/(y)+(1)/(z)`
then the electric field intensity at `(1,1,1)` is given by:
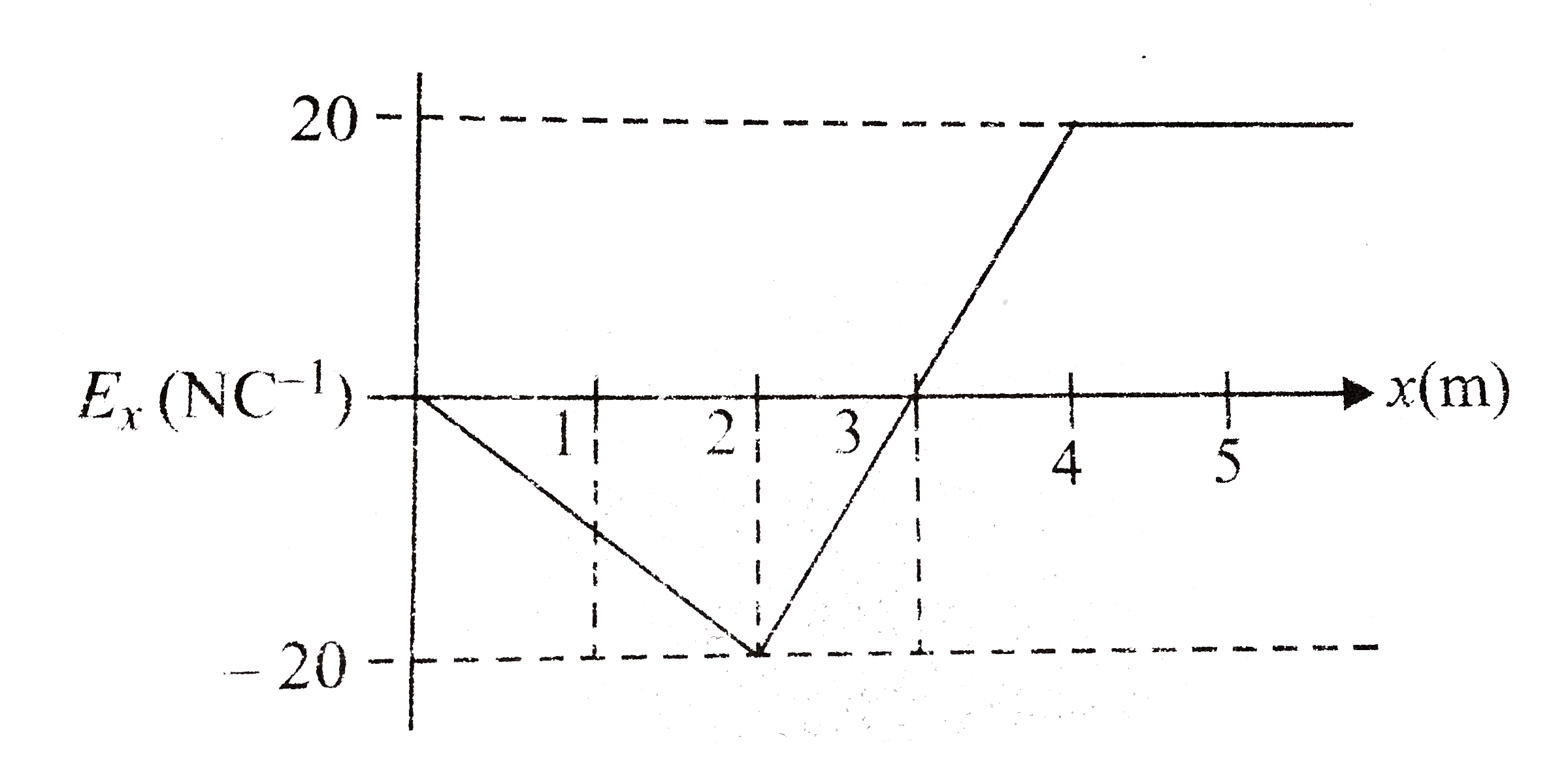
View SolutionA graph of the x-component of the electric field as a function of x in a region of space is shown in figure. The `y- and z-components ` of the electric field are zero in this region. If the electric potential is 10 V at the origin, then the potential at x = 2.0 m is
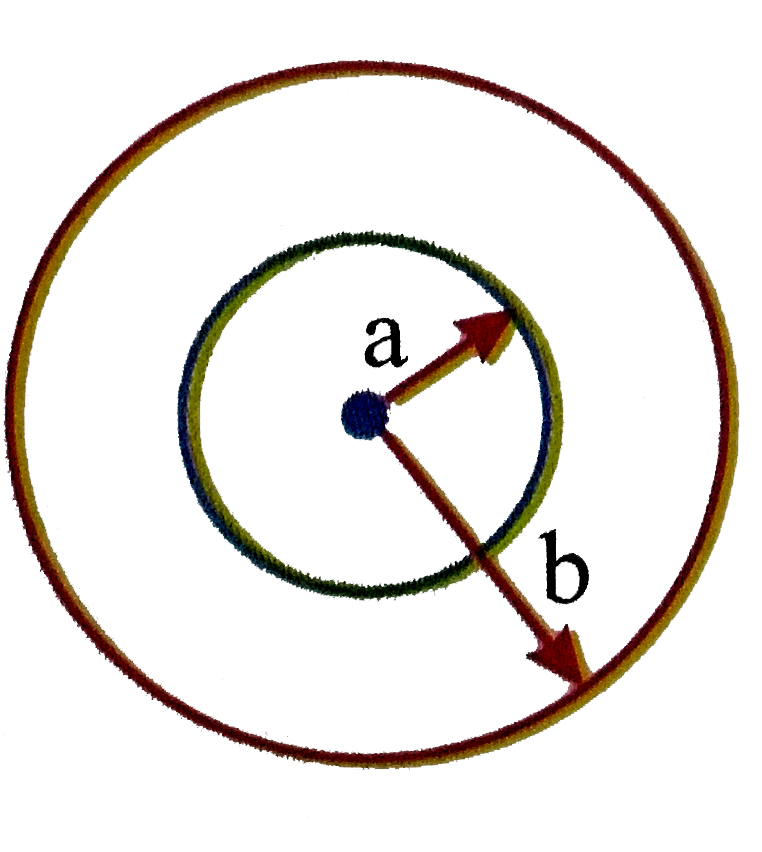
View SolutionIf the electric potential of the inner metal sphere is `10` volt & that of the outer shell is `5` volt then the potential at the centre will be
View SolutionThree concentric metallic spherical shells `A,B` and `C` of radii `a,b`and `c(a lt blt c)` have surface charge densities `-sigma ,+sigma `and -sigma `respectively ,the potential of shell `A` is
View SolutionThere are four concentric shells A,B, C and D of radii `a,2a,3a` and `4a` respectively. Shells B and D are given charges `+q` and `-q` respectively. Shell C is now earthed. The potential difference `V_A-V_C` is `k=(1/(4piepsilon_0))`
View SolutionAt distance 'r' from a point charge, the ratio `(U)/(V^(2))` (where 'U' is energy density and 'V' is potential) is best respresented by :
View SolutionSix charge of magnitude `+q` and `-q` are fixed at the cornors of a regular hexagon of edge at the cornors of a regular hexagon of edge length a as shown in the figure .The electrostatic interaction energy of the charged particle is :
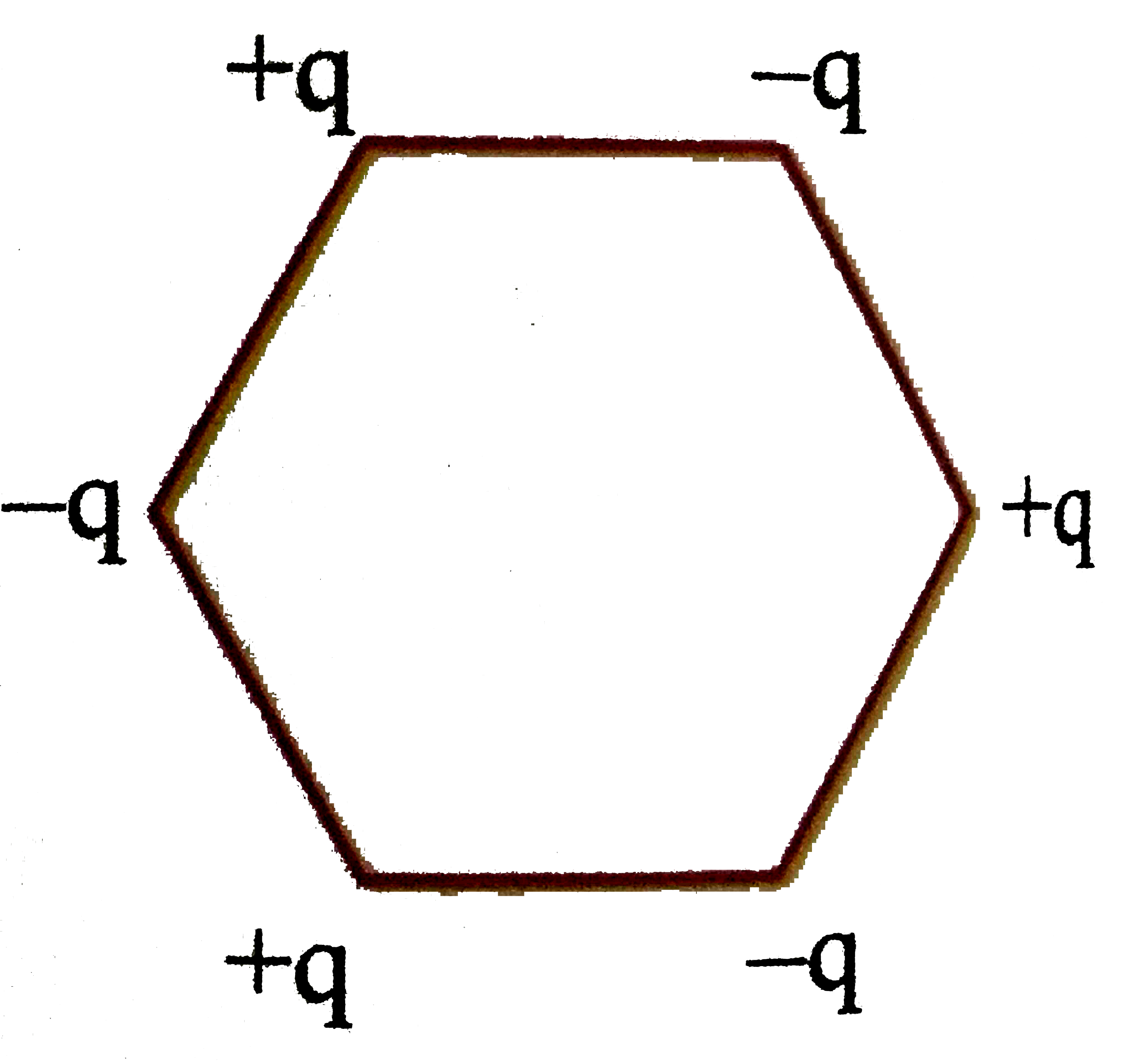
View SolutionA particle fo mass `m` carries an electric positive charge `Q` and is subjected to the combined action of gravity `g` and a unifrom horizontal electric field of strength `E`,it is projected with speed `u` to the vertical plane parallel to the electrical field and at an angle `theta `to the horizontal .The maximum distance teh particle travels horizontally when it is at the same level as its starting point is
View SolutionTwo point charges having charge +Q, –q and mass M, m respectively are separated by a distance L. They are released from rest in a uniform electric field E. The electric field is parallel to line joining both the charges and is directed from negative to positive charge. For the separation between particles to remain constant, the value of L is
`(K=(1)/(4piin_(0)))`
View SolutionA bullet of mass m and charge `q` is fired towards a solid uniformly charged sphere of radius `R ` and total charge ` + q`. If it strikes the surface of sphere with speed `u`, find the minimum speed `u` so that it can penetrate through the sphere , (Neglect all resistance forces or friction acting on bullet except electrostatic forces )
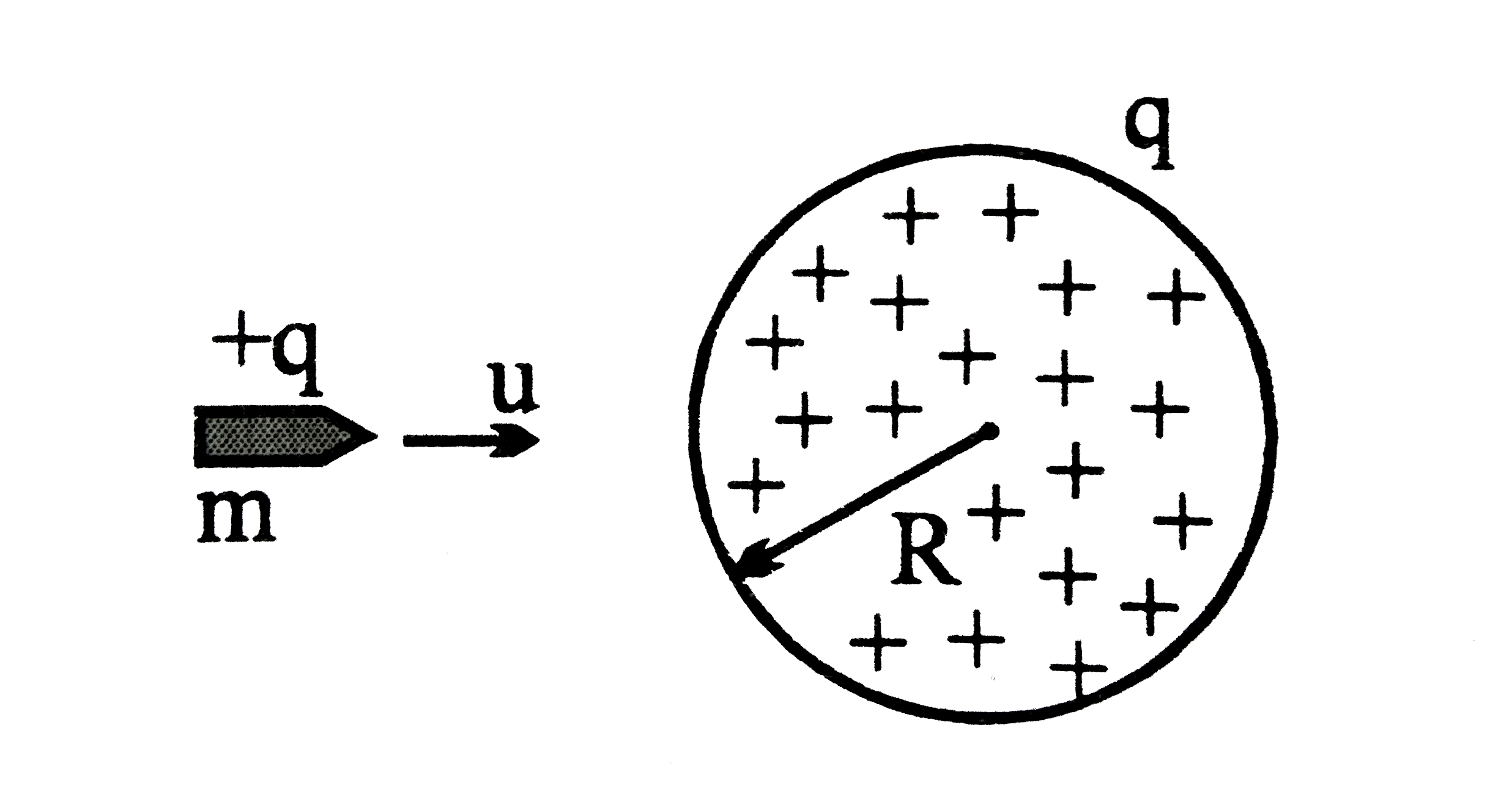 .
.
View SolutionIn space of horizontal `EF (E = (mg)//q)` exist as shown in figure and a mass m is released at the end of a light rod. If mass m is releases from the position shown in figure find the angular velocity of the rod when it passes through the bottom most position
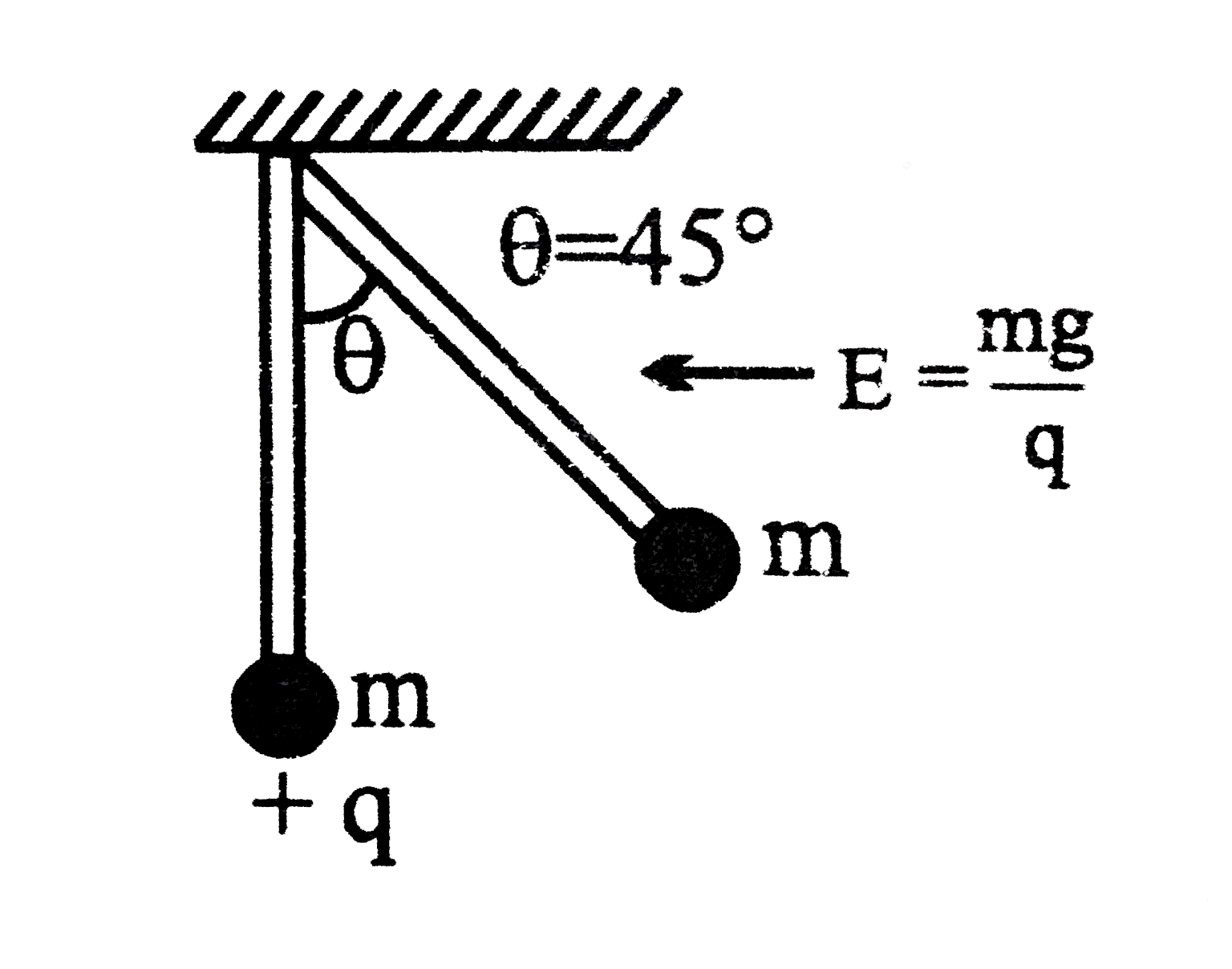 .
.
View SolutionA unit positive point charge of mass m is projected with a velocity v inside the tummel as shown. The tunnel has been made inside a uniformly charged non conducting sphere. The minimum velocity with which the point charge should be projected such that it can it reach the opposite end of the tunnel, is equal to:

View SolutionA particle of charge `-q` and mass m moves in a circle of radius r around an infinitely long line charge of linear charge density `+lamda`. Then, time period will be
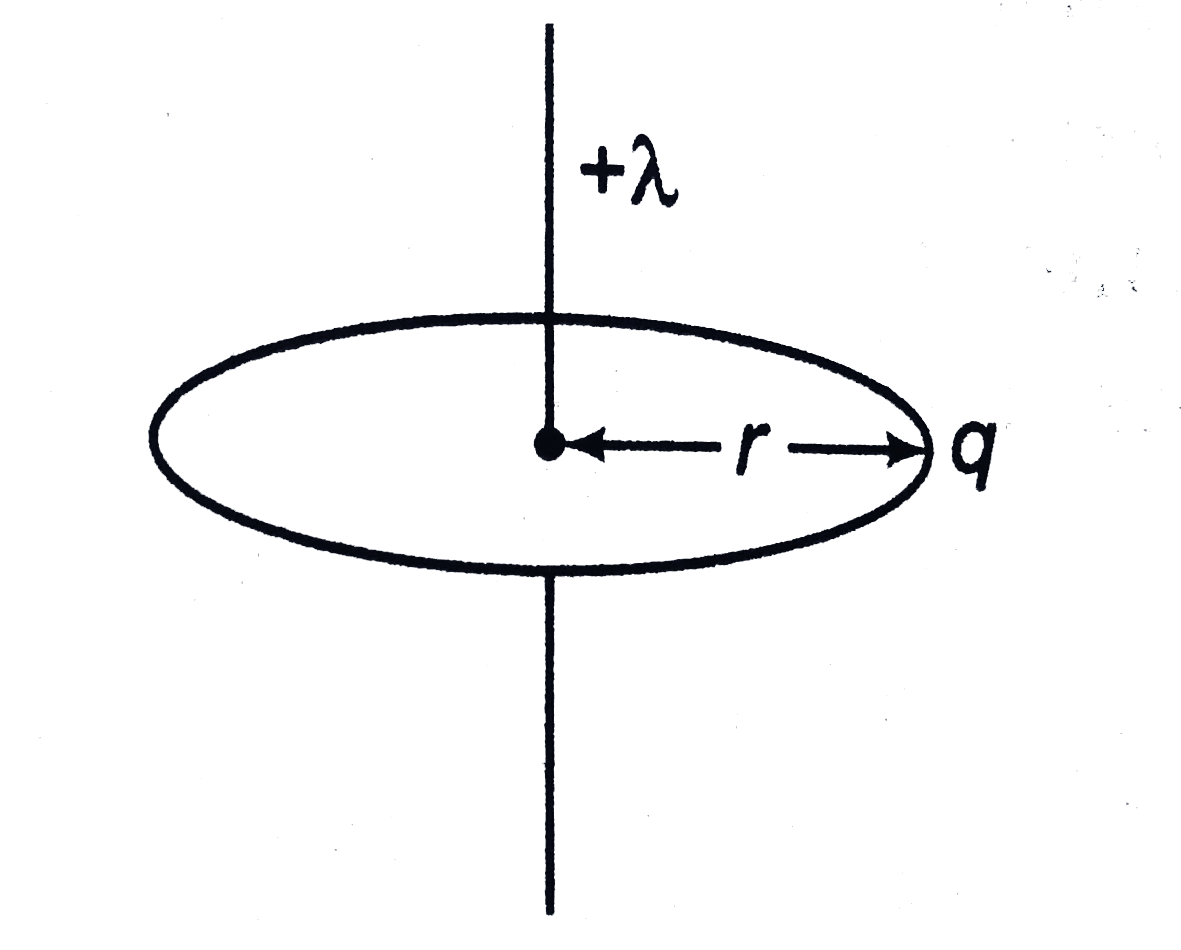 where , `k=1/4piepsilon_0)`
where , `k=1/4piepsilon_0)`
View SolutionA point mass of `-q` mass `m` is released form rest form a distance `R` along the axis of a uniform circular disc of charge `Q` Assuming gravity free situation the velocity attained by point mass when it reaches centre of disc is (Radius of disc-R)
`
View SolutionThe adjoining figure represent a semi-circular loop of charge `Q` and of radius `R` .The minimum velocity with which a point mass `m`of charge `-q` should be projected so that it becoems free from the influence of the loop is

View SolutionA charge `q` of mass `m` is projected form a long distance with speed `v` towards another stationery particle of same mass and charge the distance of closet approach of the particles is
View SolutionTwo balls of charges `q_(1)` and `q_(2)` initially have a velocity of the same magnitude and direction. After a uniform electric field has been applied for a certain time. The direction of the first ball changes by `60^(@)` and the velocity magnitude is reduced by half. The direction of velocity of the second ball changes by `90^(@)`. In what ratio will the velocity of the second ball change? Determine, the magnitude of the charge to mass ratio of the second ball if it is equal to `alpha_(1)` for the first ball. Ignore the electrostatic interaction between the balls.
 ,
,
View SolutionIn the diagram shown the charge `+Q` is fixed. Another charge `+2q` and mass M is projected from a distance R from the fixed charge. Minimum separtion between the two charge if the velocity becomes `1/sqrt3` time of the projected velocity, at this moment is (Assume gravity to be absent)
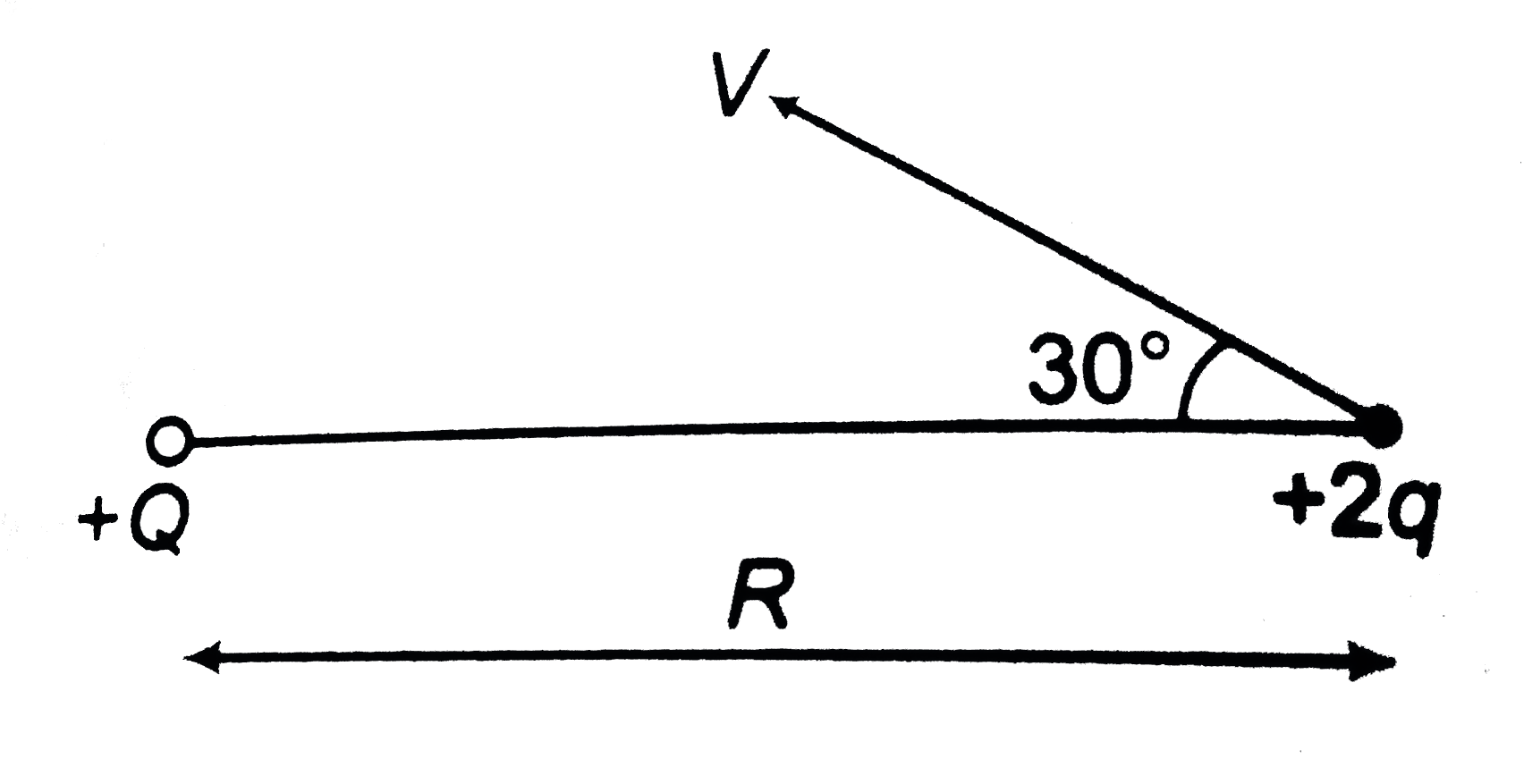
View SolutionThe dipole moment of a system of charge ` +q` distribyted uniformly on an arc of radius `R` subtending an angle ` pi //2` at its centre where another charge ` -q` is placed is :
View SolutionAs shown in the figure an electric dipole lies at a distance `x` from the centrr of a chargerd ring of radius `R` with charge `Q` uniformly distributed over it .The net force acting on the dipole is

View SolutionTwo short dipoles `phat(k)` and `P/2 hat(k)` are located at `(0,0,0)` & `(1m, 0,2m)` respectivley. The resultant electric field due to the two dipoles at the point `(1m, 0,0)` is
View SolutionA dipole of dipole moment `P` is kept at the centre of a ring of radius `R` and charge `Q` the dipole moment has direction along the ring due to the dipole is :
View SolutionAn electric dipole is placed at the origin `O` and is directed along the `x`-axis. At a point `P`, far away from the dipole, the electric field is parallel to `y`-axis. `OP` makes an angle `theta` with the `x`-axis then
View SolutionA large sheet carries uniform surface charge density `sigma` . A rod of length 2l has a linear charge density `lambda` on one half and `-lambda` on the second half. The rod is hinged at the midpoint O and makes an angle `theta` with the normal to the sheet. The torque experience by the rod is
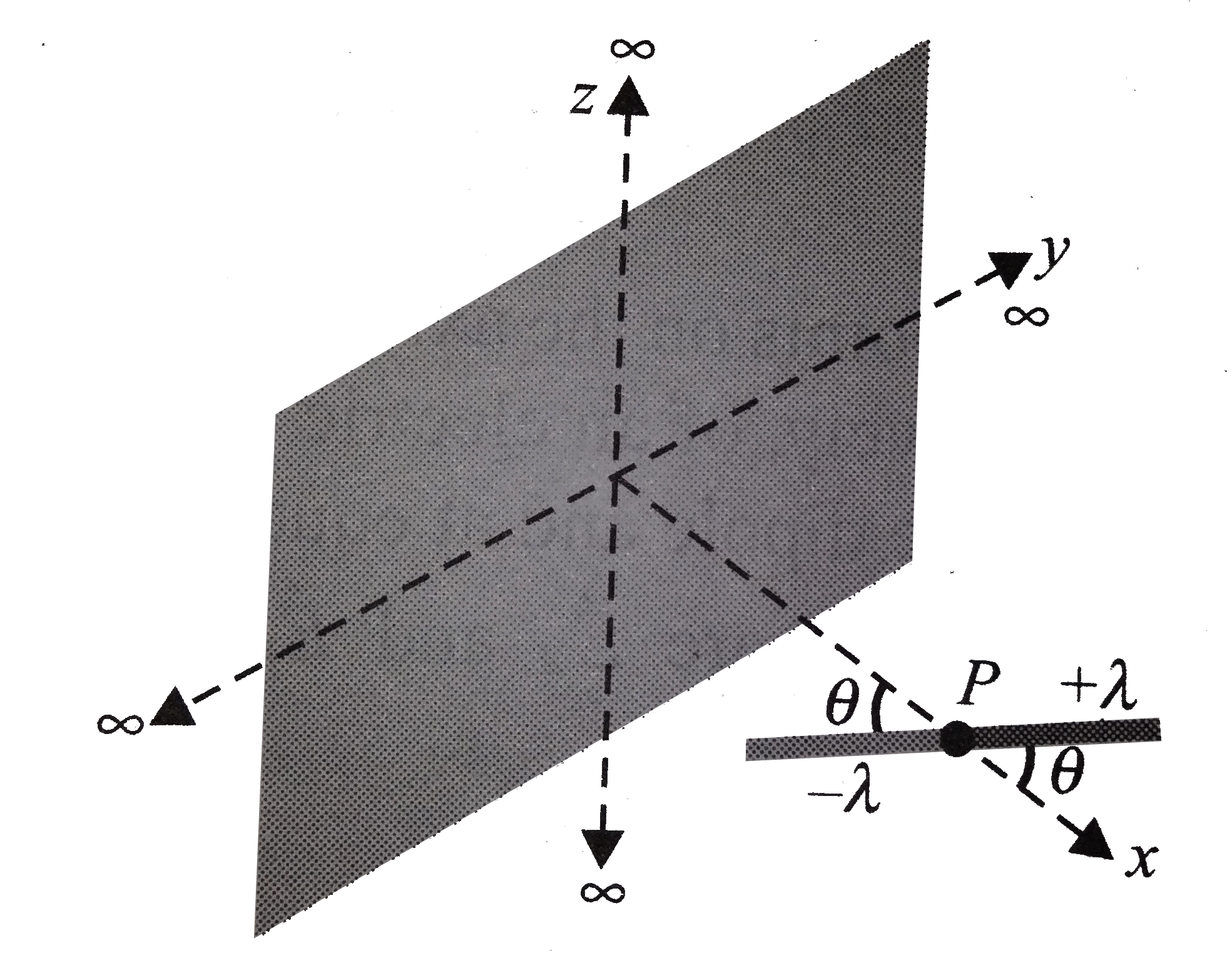
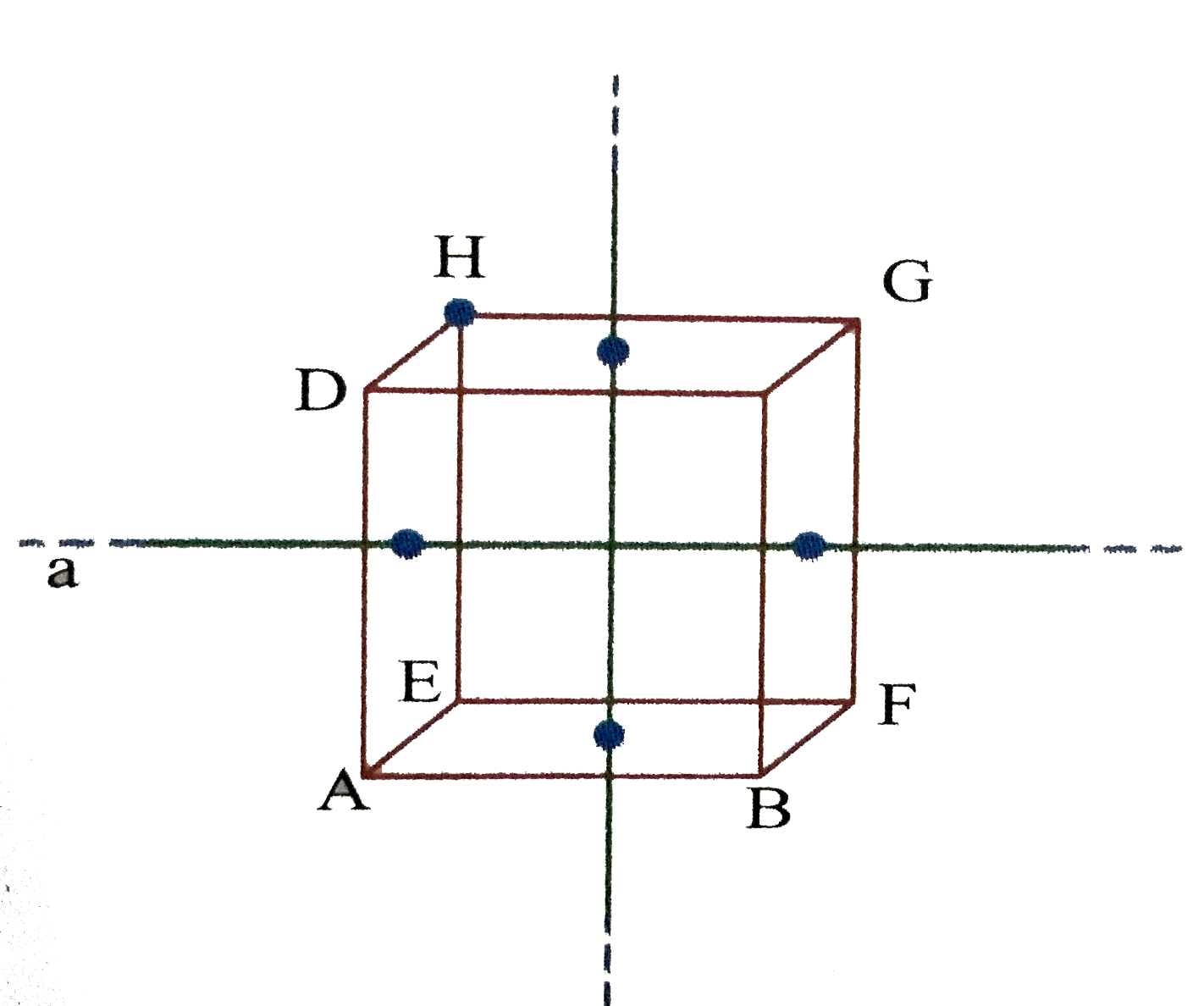
View SolutionTwo infinite line charges each having uniform charges density `lamdba` .pass through the mid points of two pairs of opposite faces of a cube of edge `L` as shown in figure .The modulue of the total electric flux due to the both the line charges through the face
View SolutionThe figure shows an imaginary cube of length `L//2` and a uniformly charged rod of length `L` touching the centre of the centre of the right face of the cube normally.At time `t=0` the rod starts moving to the left slowly at a constant speed `v` .The electric flux `(F)` thriguh the cube si plotted against time `(t)` .The correct graph showing the variation of flux with time is
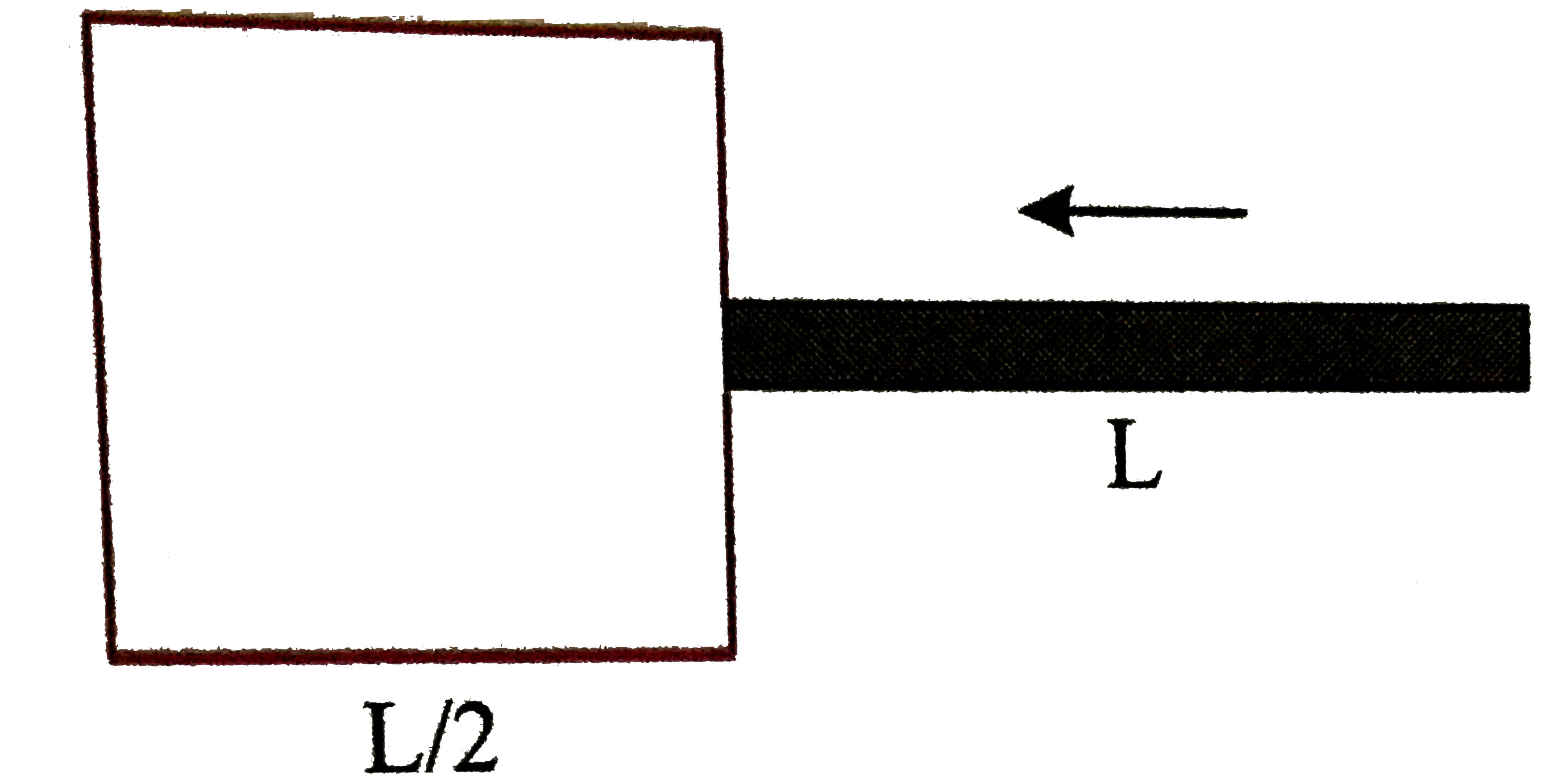
View SolutionA ring of radius `R` is placed in the plane with its centre at origin and its axis along the `x-axis` and having uniformly distributed positive charge.A ring of radius `r( ltlt R)` and coaxial with the larger ring is moving along the axis with constant velocity then the variation of electrical flux `(phi)` passing through the smaller ring with position will be best represented by :
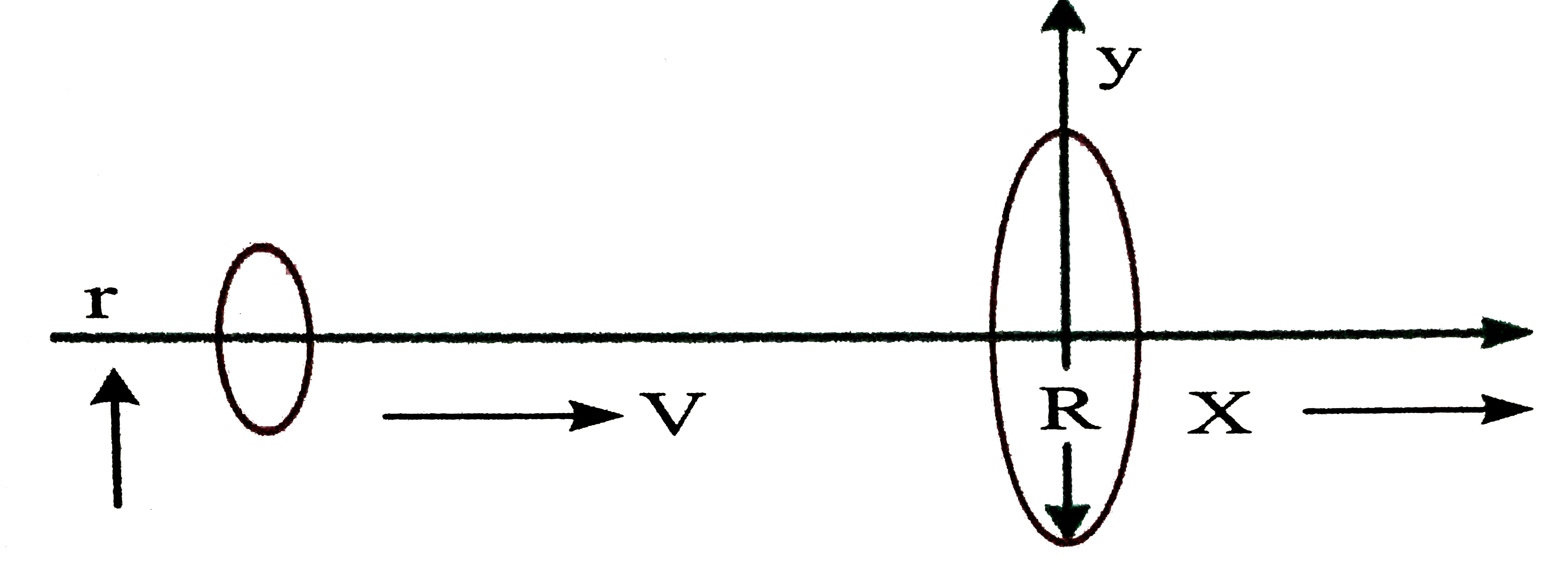
View SolutionA point charge `q` is placed at a distance `d` form the center of circular disc of radius `R`. Find electric flux through the disc due to that charge
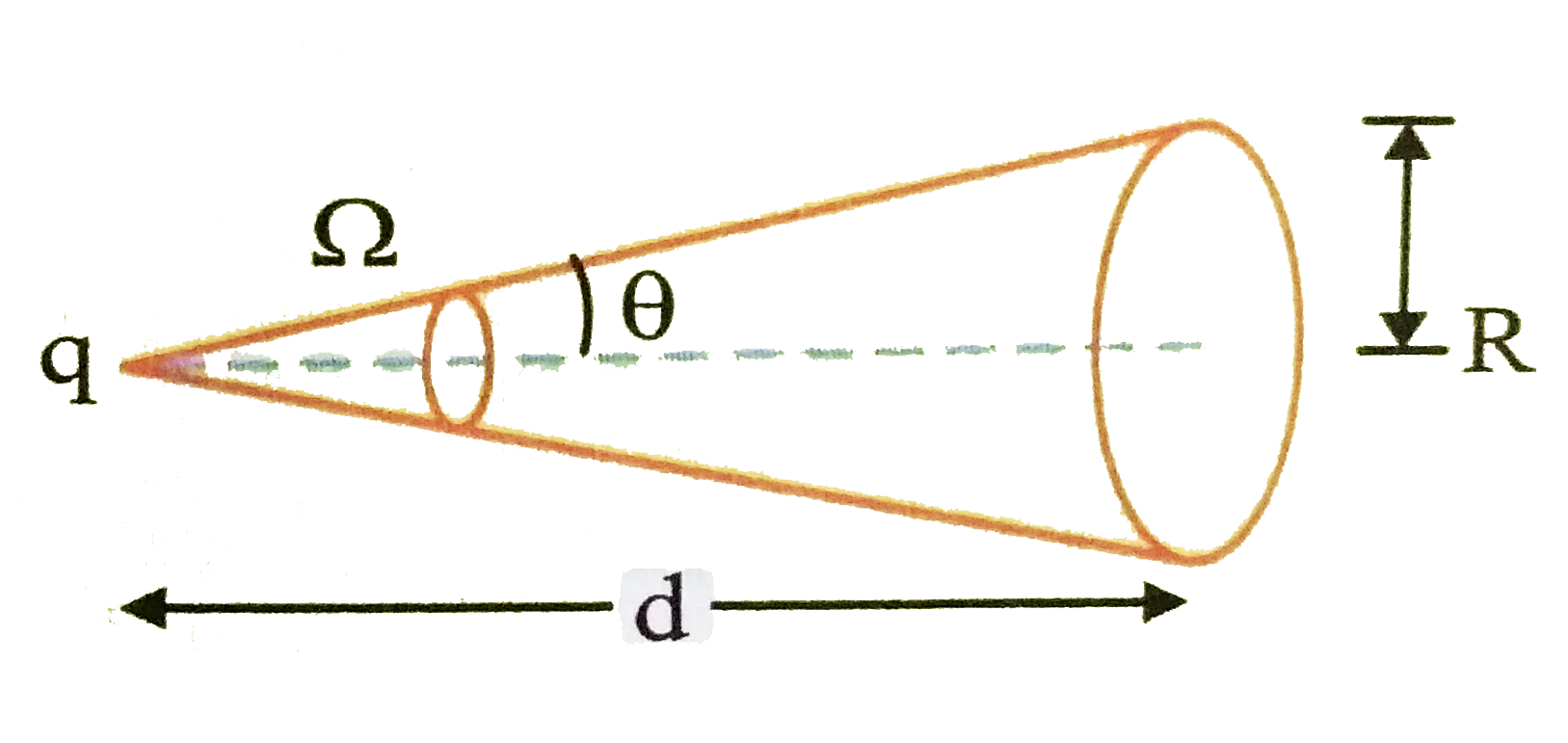
View SolutionTwo point charges `q` and `-q` are separated by the distance `2l`. Find the flux of the electric field strength vector across a circle of radius `R`.

View Solutiona point charge `q` is placed at the centre of a cylinder of length `L` and radius `R` the electric flux through the curved surface of the cylinder is
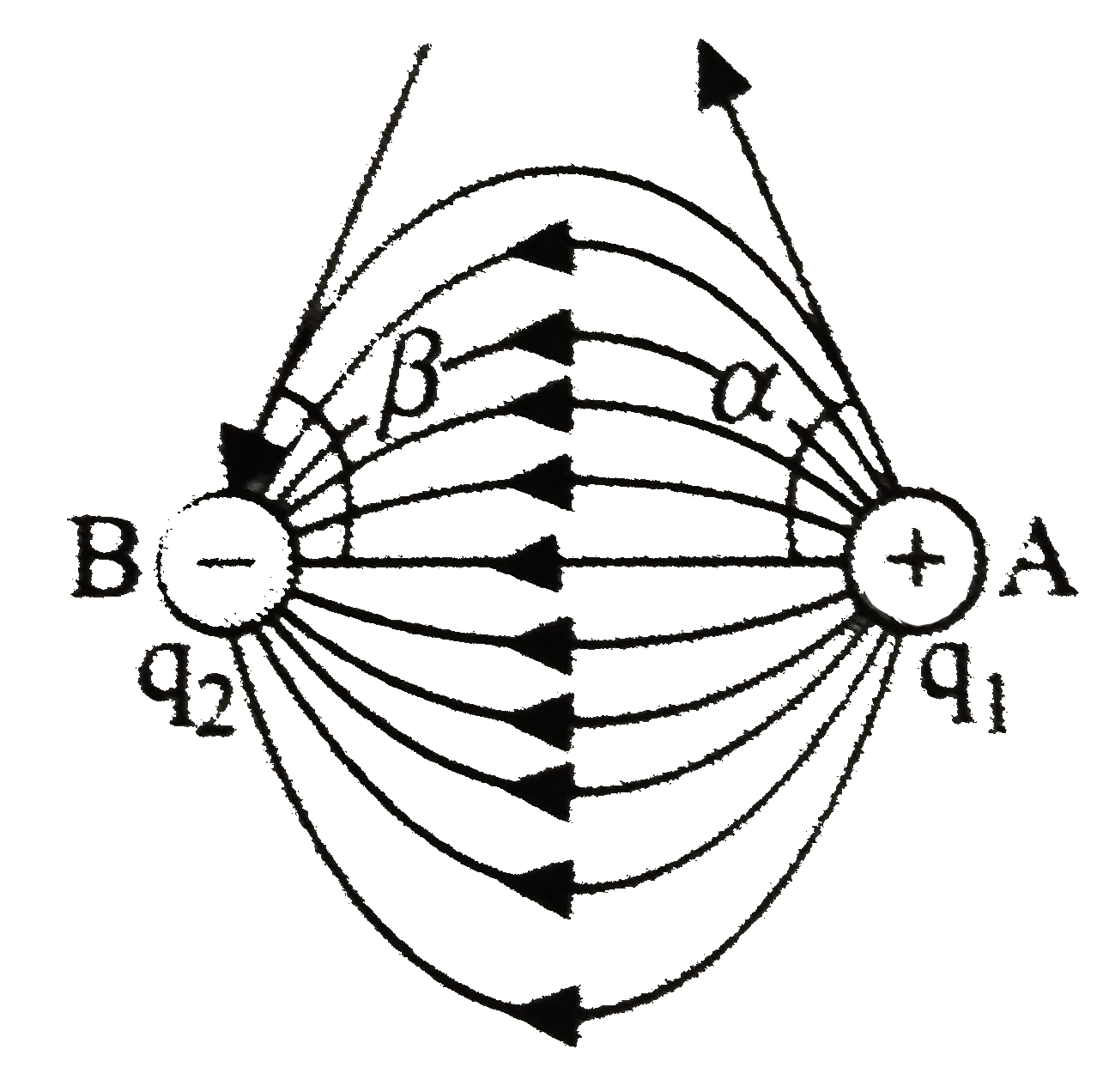
View SolutionTwo charges`+q_(1)` and `-q_(2)` are placed at A and B respectively. A line of force emanates from `q_(1)` at an angle `alpha` with the line AB. At what angle will it terminate at `-q_(2)` ?
View SolutionThe potential inside a charged ball depends only on the distance `r` of the point form its centre according to the following relation `V=Ar^(2)+B volts` The charge density inside the ball will be
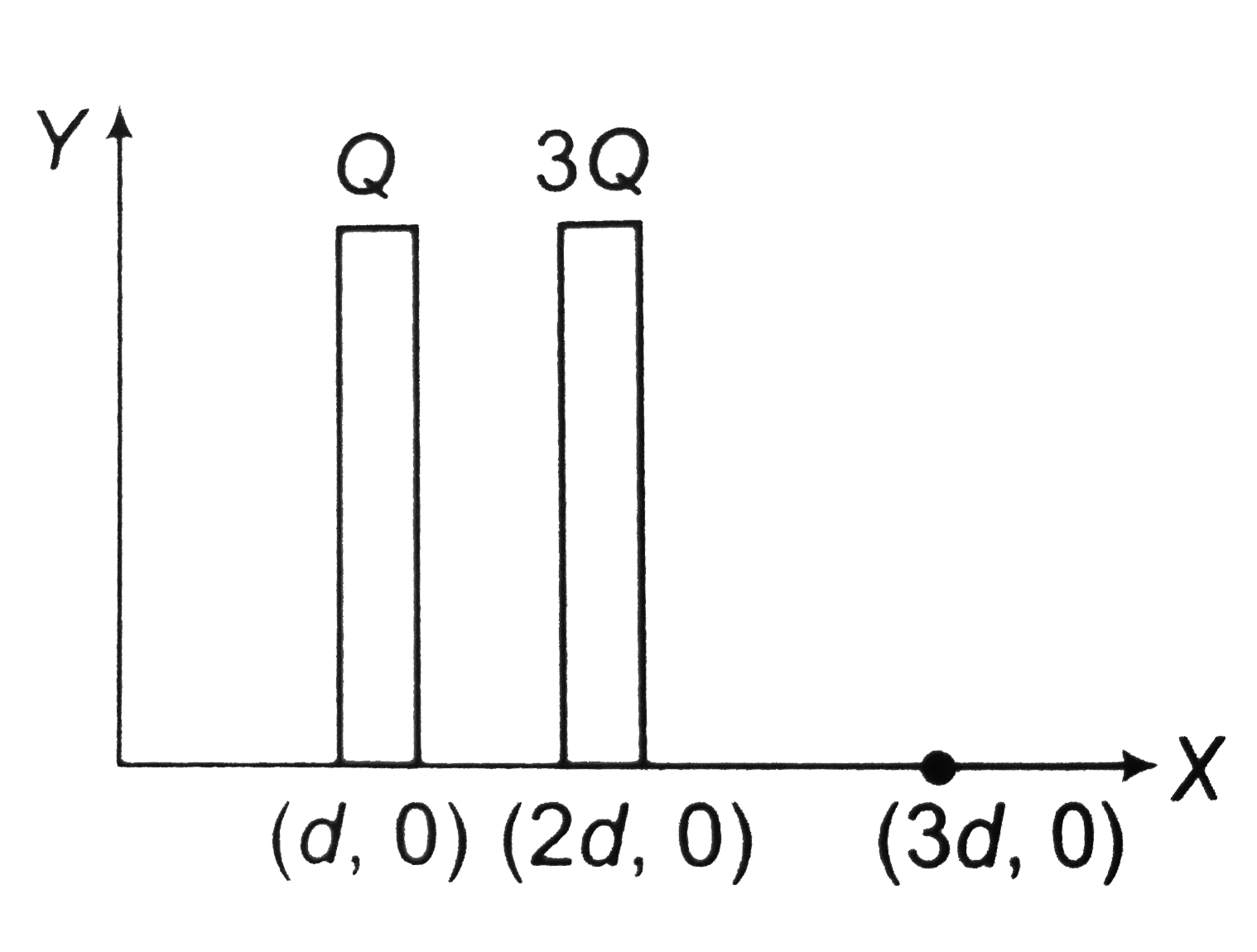
View SolutionTwo very large thin conducting plates having same cross sectional area are placed as shown in figure. They are carrying chaerges `Q` and `3Q`, respectivley. The variation of electric field as as function at x(for `x=0` to `x=3d`) will be best represented as by
View SolutionInside a ball charged uniformly with volume density `rho` there is a spherical cavity. The centre of the ball by a distance `a`. Find the field strength `E` inside the cavity, assuming the permittively equal to unity.
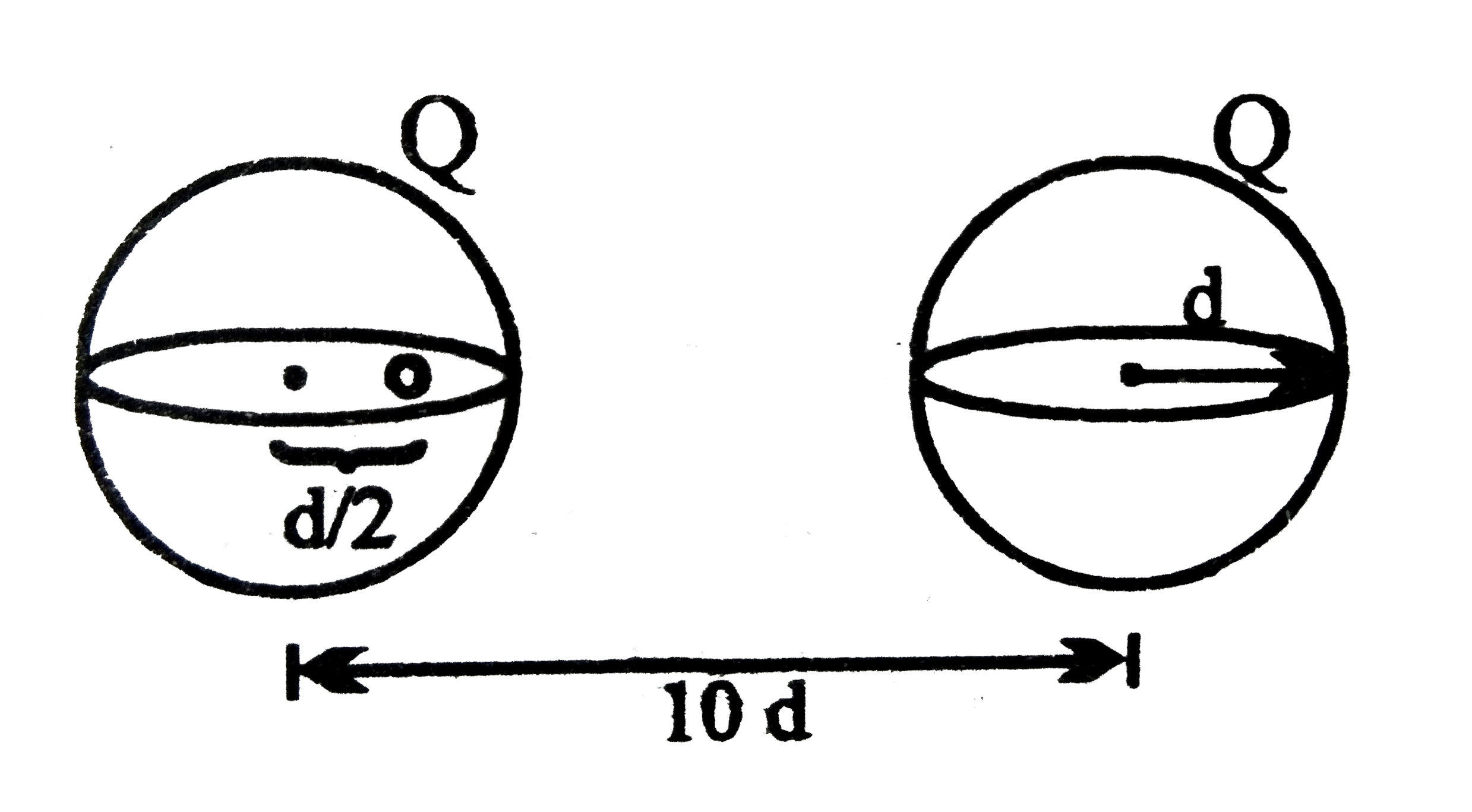
View SolutionTwo spherical , nonconducting and very tin shells of uniformly distributed positive charge `Q` and radius d are located a distance ` 10d` from each other . A positive point charge q is placed inside one of the shells at a distance ` d//2` from the center, on the line connecting the centers of the two shells , as shown in the figure, What is the net force on the charge `q` ? .
View SolutionA point charge `q` is located at the centre of the spherical layers of uniform isotropic dielectric with relative permitivity `K`.The inside radius of the layer is equal to `a` and the outside radius is equal to `b`.The electrostatic energy inside the dielectirc layer is
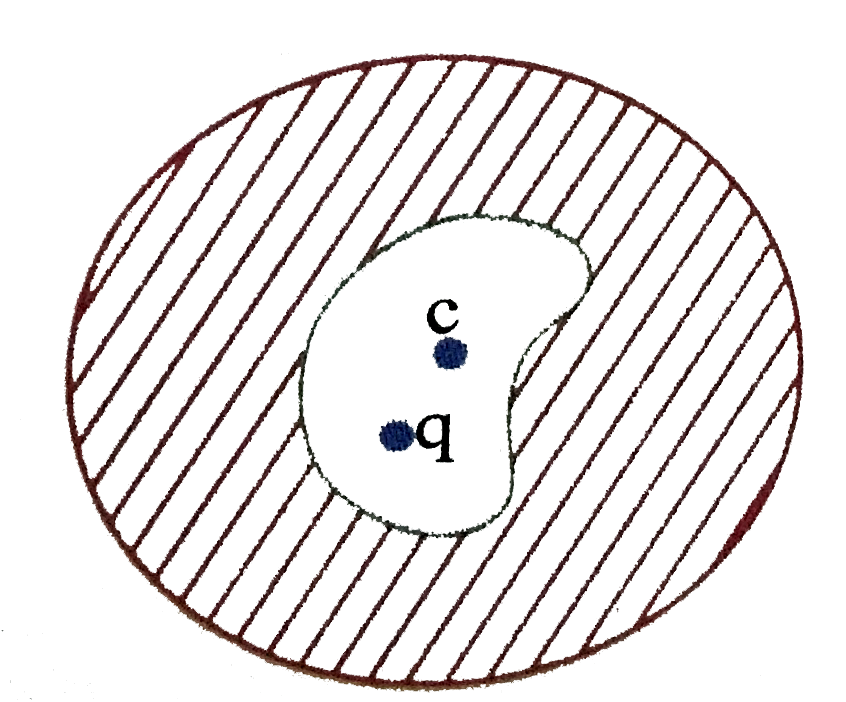
View Solutionthe figure shows a charge `q` placed inside a cavity in an uncharged conductor, Now if na external electric field is switched on
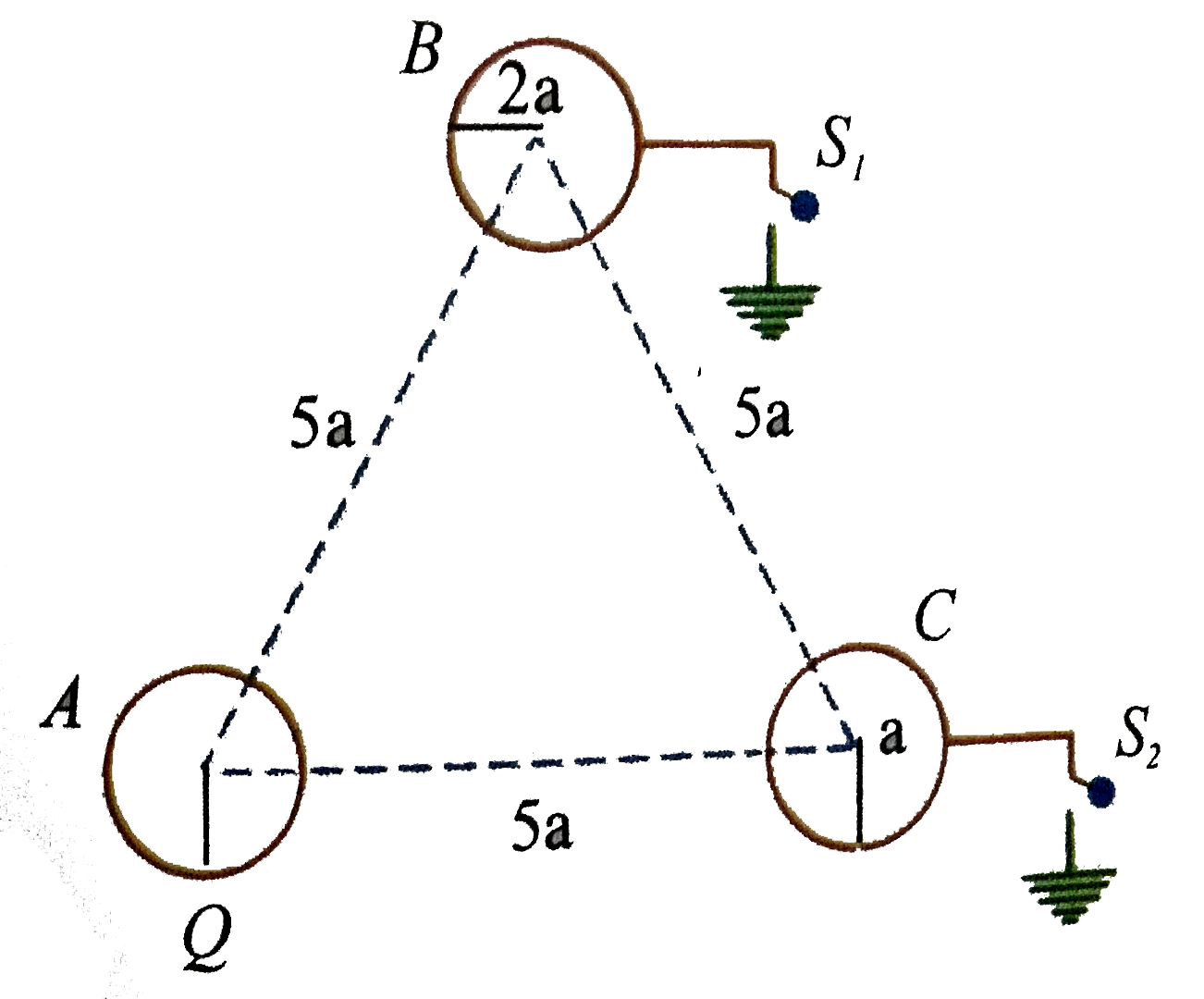
View SolutionThe following diagram shows three metal balls Ball `A` is charged to `Q` coulombs and `B,C` are unchanged .The charges on balls `B,C` when the switches `S_(1)` and `S_(2)` are closed are respectively
View SolutionIn the following diagram the conducting shells are concentric .The amount of charge that flows through the switch (S) after closing it is
View SolutionIn the following diagram that plates are conducting and are held parallel then amount of charge that flows through the switch after closing it is
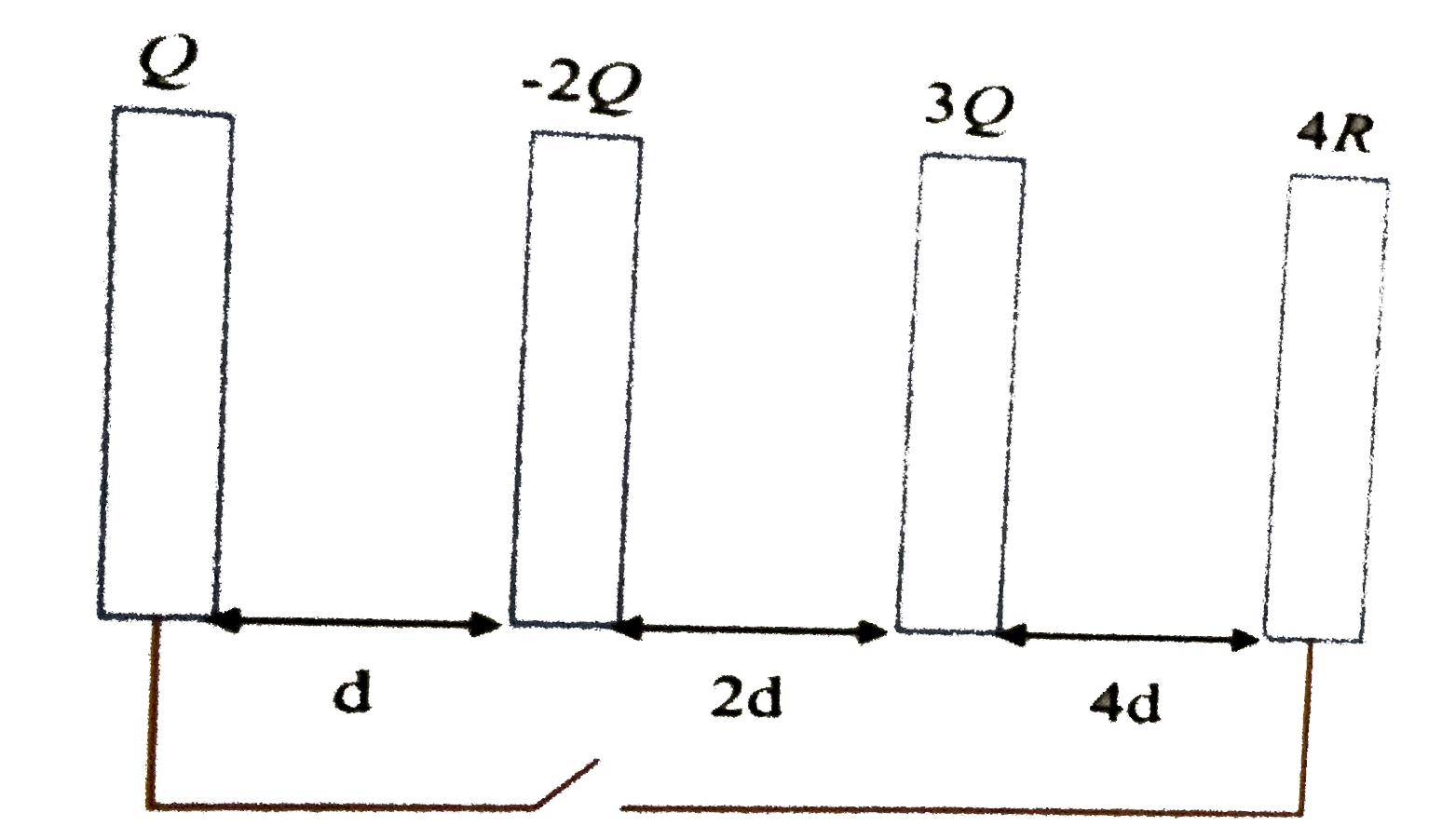
View SolutionTwo concentric thin conducting sphereical shells having radii `R` and `2R` are as shown in the figure .A charge `+Q` is given to the shell `A` and `-4Q` is given to the shell `B` .If `A` and `B` are connected by a thin conducting wire then the amount of heat produced after the connection is

View SolutionFive balls numbered 1,2,3,4,and 5 are suspended using separated threads. The balls (1,2),(2,4) and (4,1) show electrostatic attraction while balls (2,3) and (4,5) show repulsion. Therefore, ball 1 must be
View SolutionA point charge `q` is placed at orign Let ` vec E_A, vec E_B ` and `vec E_C ` be the electric field at theree points ` (A) ( 1, 2, 3 ), B (1,1,-1)` and ` C( 2,2,2) ` due to charge `q`. Then-
[i] ` vec E_A _|_ vec E_B`
[ii] `|vec E_B |=4|vecE_(c)|`
select the correct alternative .
View SolutionA negative point charge placed at the point `A` is

View SolutionFour charges of `1mC,2mC,3mC` and `-6mC` are placed one at each corner of the square of side `1m`.The square lies in the `x-y` plane with its centre at the origin
View SolutionTwo fixed charges `4Q` (positive) and `Q` (negative) are located at `A` and `B`the distance `AB` being `3m`
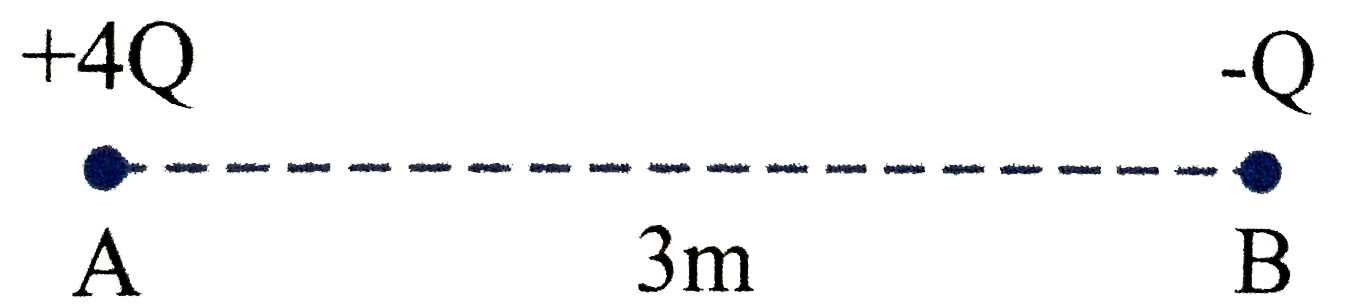
View SolutionTwo identical charges `+Q` are kept fixed some distance apart.A small particles `P` with charge `q` is placed midway between them . If `P` is given a small displacement `Delta` ,it will undergo simple harmonic motion if
(i) `q` is positive and `Delta` is along the line joining the charges
(ii) `q` is positive and `Delta` is perpendicular to the line joining the charges
(iii) `q` is negative and `Delta` is perpendicular to the line joining the charges
(iv) `q` is positive and `Delta` is along the line joining the charges
View SolutionSelect the correct statement :(Only force on a particle is due to electric field)
View SolutionTwo point charges Q and ` - Q //4` are separated by a distance ` X`. Then
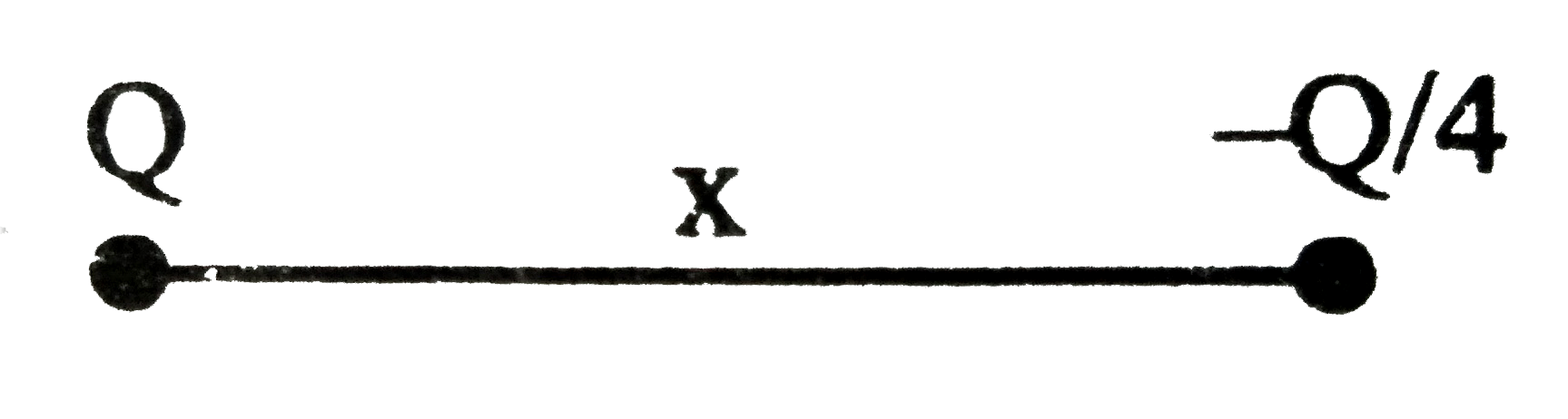 .
.
View SolutionThree point charge `Q,4Q` and `16Q` are placed on a straight line `9`cm long.Charges are placed in such a way that the system has minimum potential energy .Then
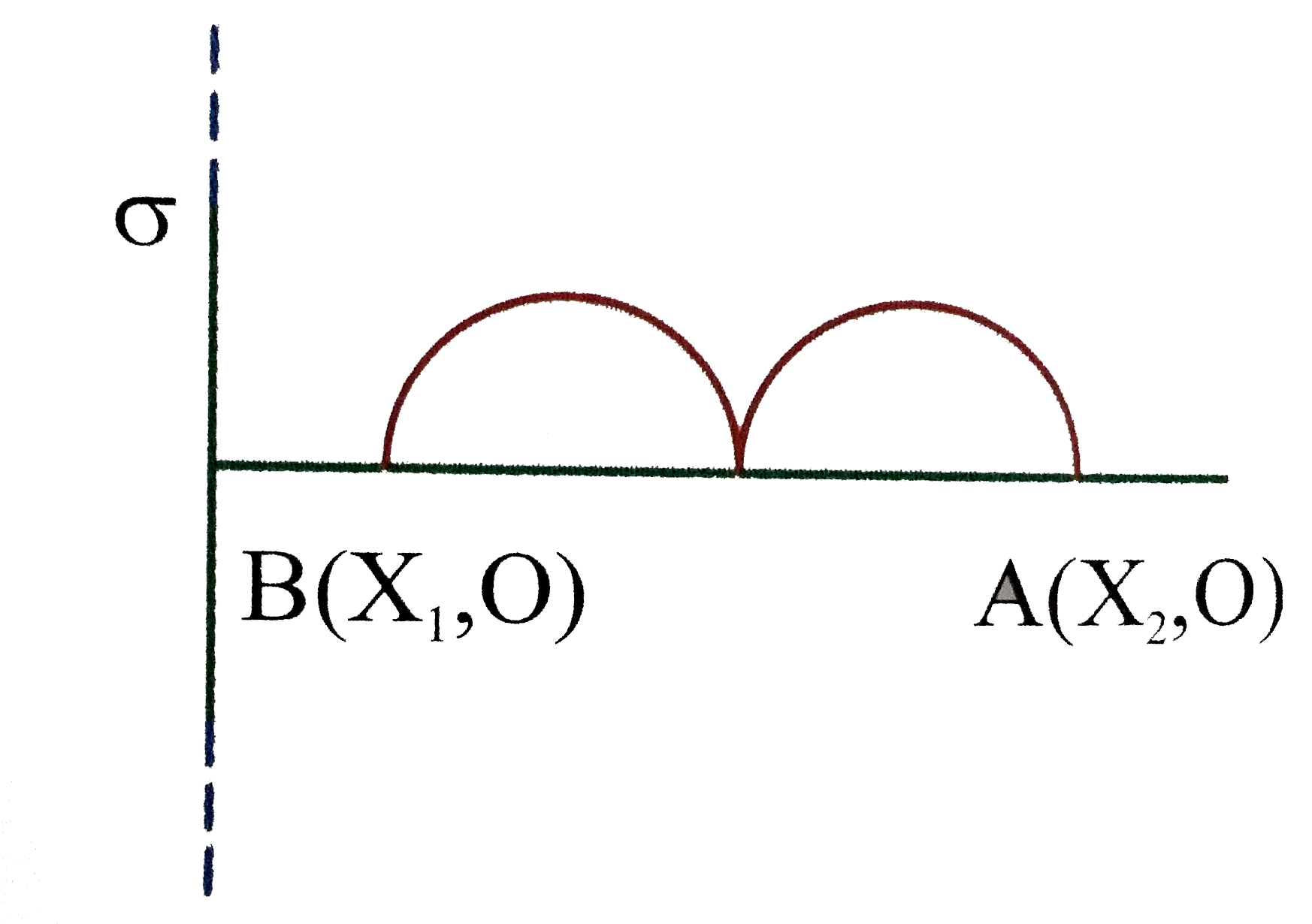
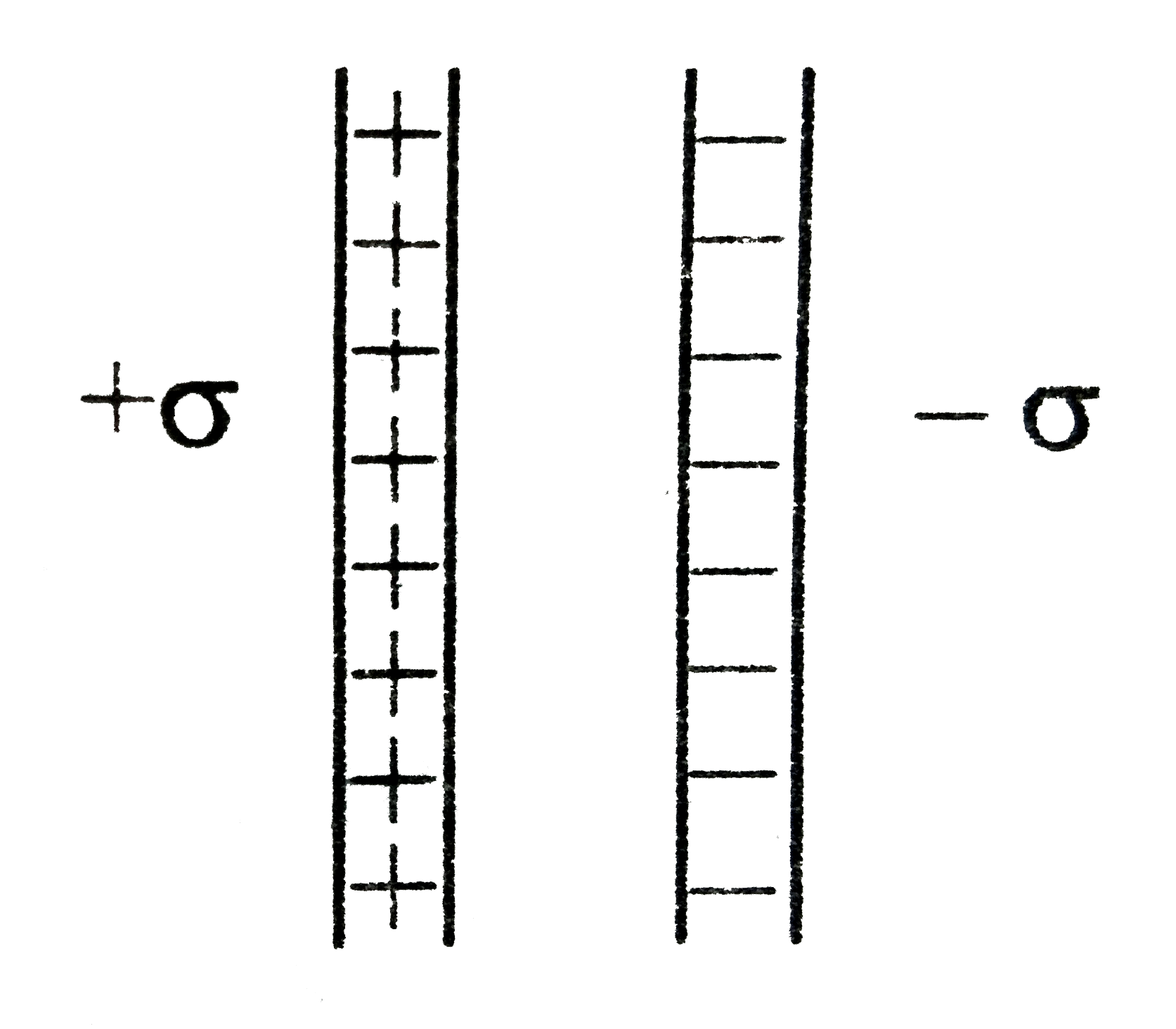
View SolutionTwo infinite sheets of uniform charge density ` + sigma` and ` - sigma` are parallel to each other as shown in the figure . Electric field at the
 .
.
View SolutionIf we use permitivity `epsilon`, resistance `R`, gravitational constant `G` and voltage `V` as fundamental physical quantities, then:
View SolutionA thin walled spherical conducting shells `S` of radius `R` is given charge `Q`,the same amount of charge is also placed at its centre `C`.Which of the following statements are correct.
View SolutionA hollow closed conductor of irregular shape is given some charge . Which of the following statements are correct ?
View Solutionthree points charges are placed at the cornors of an equilibrium triangle of side `L` as shown in the figure `
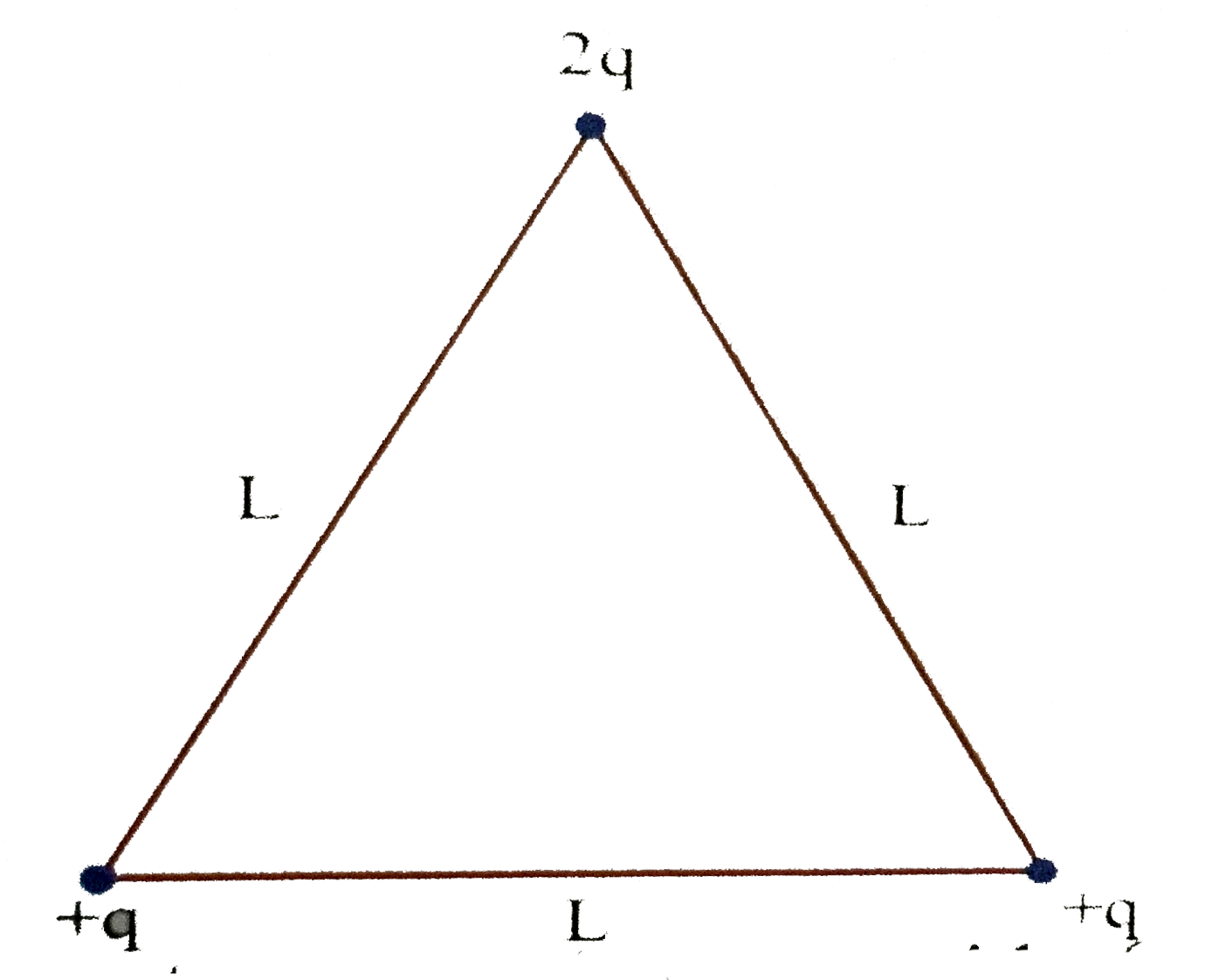
View SolutionAn electric dipole is placed at the centre of a sphere. Mark the correct options:
View SolutionAn electric field converges at the origin whose magnitude is given by the expression `E=100r N//C`, where r is the distance measured from the origin.
View SolutionA conducting sphere `A` of radius `a` ,with charge `Q` , is placed concentrically inside a conducting shell `B` of radius `b` . `B` is earthed. `C` is the common centre of the `A` and `B`
View SolutionTwo thin conducting shells of radii `R` and `3R` are as shown in the fig. External shell carries a charge `+Q` and inner shell neutral. The inner shell is earthed with the help of a switch `S`. Then

View Solution`X` and `Y` are large, parallel conducting plates close to each other. Each face has an area `A`. `X` is given a charge `Q`. `Y` is without any charge. Points `A,B` and `C` are as shown in the figure.

View SolutionA particle of mass m and charge `q` is thrown in a region where uniform gravitational field and electric field are present . The path of particle -
View SolutionTwo large parallel conducting plates are placed close to each other ,the inner surface of the two plates have surface charge densities `+sigma` and `-sigma` .The outer surfaces are without charge.The electric field has a magnitude of
View Solutionthe electric potential in the region of space is given by :`V(x)=A+Bx+Cx^(2)` where `V` is in volts,`x` is in meters and `A,B,C` are constants.Then,
View SolutionA dipole is placed in `x-y` plane parallel to the line `y=2x` there exist a unifrom electric field among `z-axis` .Net force acting on the dipole will be zero.But it can experience some torque,we can show that the direction of this torque will be parallel to the line
View SolutionA 10 C charge is given to a conducting spherical shell, and a-3 C point charge is placed inside the shell. For this arrangement, find the correct statement(s).
View SolutionFor Gauss 'law mark out the corrrect statement(s)
View SolutionTwo infinite parallel,non- conducting sheets carry equal positive charge density `sigma` ,One is placed on the other at distance `x=a` Take potential `V=0` at `x=0` then
View SolutionConsider two large ,identical paralllel conducting plates having surface `X` and `Y` .facing eacg other.The charge per unit area on `X` is `sigma_(1)` and charge perunit surface area of `Y` is `simga_(2)` .Then,
View SolutionA particle having charge 's' starts from rest in a region where the electric field has constant direction but magnitude varying with time `t` as `E=E_(0)t` .In time `t`, it is observed that the particle acquire a velocity `v` after covering a distance `x` then
View SolutionTwo charge `Q_(1)` and `Q_(2)` are placed at the points `A` and `B` having separation `r` lying inside and outside the unchanged conducting shell. The force on `Q_(1)` is `F` and that on `Q_(2)` is `f`.Then
View SolutionIn a parallel capacitor the potential difference between the plates is `V` ,A particle of mass `m` and charge `-Q` leaves the negative plate and reaches the positive plate at distance `d` in time `t` with a momentum `p` .Then
View Solution
Level V questions and complete solutions for chapter ELECTROSTATICS AND GAUSS LAW of NARAYANA PHYSICS (HINGLISH) of Class 12