Complete Solutions to ILLUSTRATION of chapter RAY OPTICS AND OPTICAL INSTRAUMENTS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | RAY OPTICS AND OPTICAL INSTRAUMENTS |
| NARAYANA | ILLUSTRATION |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Demostrate that a light beam reflected from three mutually perpendicular plane mirrors in succession reverses its direction.
View SolutionTwo plane mirrors are inclined at an angle of `70^(@)` to each other. Find the number of images formed when object is placed as shown in figure.

View SolutionFind the number f images formed by three mirrors AB, BC and AC in situation as shown in figure. The object is at the centre of tringle

View SolutionFigure shows a point O i.e. the object placed between two parallel mirrors. Its distance from is 2 cm and that from is 8 cm. find the distance of images from the two mirrors considering reflection reflection on mirror first.

View SolutionAn object moves with `5ms^(-1)` toward right while the mirror moves with `1ms^(-1)` toward the left as shown in Figure. Find the velocity of image.

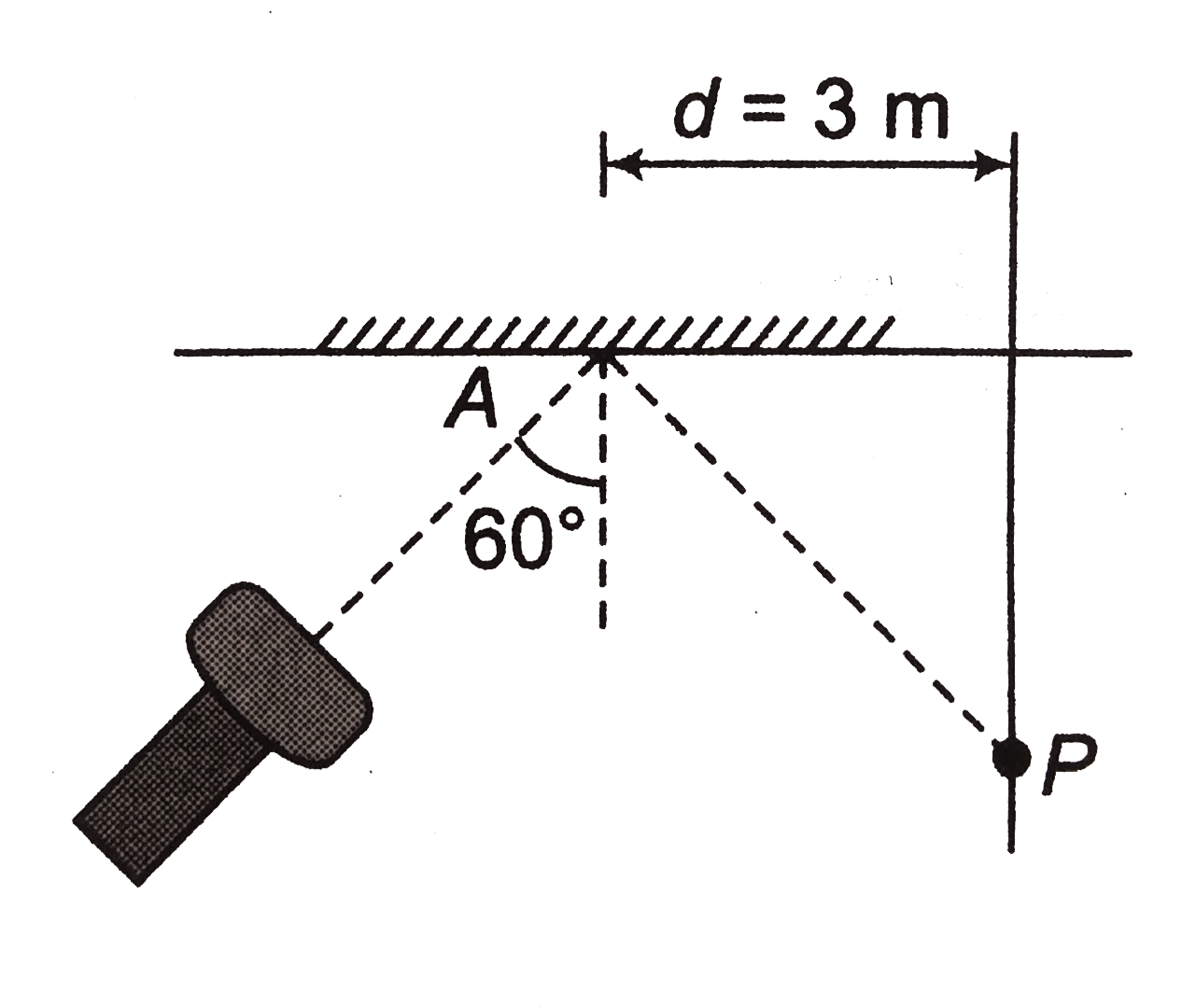
View SolutionFigure shows a torch producing a straight light beam falling on a plane mirror at an angle `60^(@)` The reflected beam makes a spot P on the screen along y-axis . If at t=0, mirror starts ratating about the hinge A with an angular velocity `(omega)=1^(@)` per second clockwise. Find the speed of the spot on screen after time t = 15 s.
View SolutionFind the minimum size of mirror required to see the full image of a wall behind a man standing at the centre of room, where H is the height of wall

View SolutionA ray of light travelling in the direction `1/2 (hati+sqrt(3)hatj)` is incident on a plane mirror. After reflectiion, it travels along the direction `1/2(hati -sqrt(3)hatj)`. The angle of incidence is
View SolutionA plane mirror is placed at origin parallel of y-axis, facing the positive x-axis. An object starts from (2m, 0, 0) with a velocity of `(2hat(i)+2hat(j))m//s`. The relative velocity of image with respect to object is along
View SolutionA reflecting surface is represented by the equation
`y = (2L)/(pi) sin ((pi x)/(L))`, where `0 le x le L`. A ray of light travelling horizontally becomes vertical after reflection with the surface. The co-ordinates of the point where this ray is incident is.
View SolutionThe focal length of a concave mirror is `30`cm.Find the position of the object in front of the mirror,so that the image is there times the size of the objects.
View SolutionA reflecting surface is represented by the equation `x^(2) + y^(2) = a^(2)`. A ray travellingin negative x-direction is directed towardspositive y-direction after reflection from thesurface at point P. Then co-ordinates of point P are

View SolutionA point light source lies on the principal axis of concave spherical mirror with radius of curvature 160 cm. Its image appears to be back of the mirror at a distance of 70 cm from mirror. Determine the location of the light source.
View SolutionA point source of light is located 20 cm in front of a convex mirror with f=15 cm. Determine the position and nature of the image point.
View SolutionAn object is 30.0 cm from a spherical mirror along the central axis. The absolute value of lateral magnification is `(1)/(2)`. The image produced is inverted. What is the focal length of the mirror?
View SolutionAn object of length 10 cm is placed at right angles to the principal axis of a mirror of radius of curvature 60 cm such that its image is virtual, erect and has a length 6cm. What kind of mirror is it and also determine the position of the object?
View SolutionAn object is placed in front of a convex mirror at a distance of 50cm. A plane mirror is introduced covering the lower half of the convex mirror. If the distance between the object and the plane mirror is 30cm, it is found that there is no parallax between the images formed by the two mirrors. What is the radius of curvature of the convex mirror?
View SolutionA concave mirror of focal length 10cm and a convex mirror of focal length 15cm are placed facing each other 40cm apart. A point object is placed between the mirrors, on their common axis and 15cm from the concave mirror. Find the position and nature of the image produced by successive reflections, first at the concave mirror and then at the convex mirror.
View SolutionFind the velocity of image w.r.t. ground.

View SolutionFind the velocity of image w.r.t grounds

View SolutionThe image of a real object in a convex mirror is 4cm from the mirror. If the mirror has a radius of curvature of 24cm, Find the position of object and magnification
View SolutionFind the velocity of image in a situation as shown in the figure

View SolutionA point object located at a distance of 20 cm from the pole of a concave mirror of focal length 30 cm with height 2 cm is moving with a velocity `( bar(V_(OG)) =4 hati - 5 hatj)` m/s and velocity of the mirror is `(bar(V_(mg)) = -6 hati + 10 hatj)` m I s as shown. Find the velocity of image w.r.t ground.
View SolutionTwo concave mirrors, each having radius of curvature 40 cm are placed such that their principle axes are parallel to each other and at a distance of 1 cm to each other. Both the mirrors are at a distance of 100 cm from each other. Considering first reflection at `M_(1)` and then at `M_(2)` , find the coordinates of the image thus formed object as the origin.

View SolutionThe refractive index of glass with respect to water is `(9)/(8)`. If the velocity of wavelength of light in glass are `2 xx 10^(8) m//s` and 4000 Å respectively, find the velocity and wavelength of light in water.
View SolutionThe wavelength of light in vacuum is `lambda_(0)` . When it travels normally through glass of thickness 't'. Then find the number of waves of light in ‘t’ thickness of glass (Refractive index of glass is `mu`)
View SolutionWhen light of wavelength `lambda_(0)` in vacuum travels through same thickness ‘t’ in glass and water, the difference in the number of waves is. (Refractive indices ofglass and water are `mu_(g)` and `mu_(w)` respectively.)
View SolutionThe optical path of a monochromatic light is the same if it travels through 4 cm of glass or 4.5 cm of water . If the refractive index of galss is 1.5, then the refractive index of water is
View SolutionFind the thickness of a plate which will produce a change in optical path equal to half the wavelength `lamda` of the light passing through it normally. The refractive index of the plate is `mu`.
View SolutionConsider slabs of three media A, B and C arranged as shown in figure R.I. of A is 1.5 and that of C is 1.4. If the number of waves in A is equal to the number of waves in the combination of B and C then refractive index of B is:

View SolutionTwo parallel rays are travelling in a medium of refractive index `mu_(1)=4/3` . One of the rays passes through a parallel glass slab of thickness t and refractive index `mu_(2)=3/2` The path difference between the two rays due to the glass slab will be
View SolutionA ray of light passes through a glass slab of thickness t and refractive index `mu` . If the speed of light in air be 'c', the time taken by the ray to cross through the plate is _______
View SolutionA light ray is incident on a plane glass slab of thickness ‘t’ at an angle of incidence ‘i’ as shown in the figure. If `mu` is the refractive index of glass. Then find time taken by the light ray to travel through the slab.
View SolutionLight of wavelength `4500^(@)` in air is incident on a plane boundary between air and another medium at an angle `30^(@)` with the plane boundary. As it enters from air into the other medium, it deviates by `15^(@)` s towards the normal Find refractive index of the medium and also the wavelength of given light in the medium.
View SolutionMonochromatic light falls at an angle of incidence i on a slab of a transparent material (refractive index `mu`). If reflected and refracted rays are mutually perpendicular, find the relation between `mu` and `i`.
View SolutionA ray of light is incident at the glass-water interface at an angle i as shown in figure, it emerges finally parallel to the surface of water, then the value of `mu_(g)` would

View SolutionA light beam is travelling from region I to region IV- (Refer figure). The refractive index in regions I, II,III and IV are `n_(0), n_(0)/2 , n_(0)/6 "and" n_(0)/8` respectively. The angle of incidence `theta` for which the beam just misses entering region TV is

View SolutionA ray of light passes through four transparent media with refractive indices ` mu_(1), mu_(2), mu_(3)` and `mu_(4)` as shown in the figure. The surfaces of all media are parallel. If the emergent ray CD is parallel to the incident ray AB, we must have

View SolutionThe x-z plane separates two media A and B of refractive indices `mu_(1) = 1.5` and `mu_(2) = 2`. A ray of light travels from A to B. Its directions in the two media are given by unit vectors `u_(1) = a hat(i)+b hat(j)` and `u_(2) = c hat(i) +a hat(j)`. Then
View SolutionA ray of light falls on the surface of a spherical glass paper weight making an angle `alpha` with the normal and is refracted in the medium at an angle `beta`. The angle of deviation of the emergent ray from the direction of the incident ray is :
View SolutionA ray of light falls on a transparent sphere with centre at C as shown in figure. The ray emerges from the sphere parallel to line AB. The refractive index of the sphere is

View SolutionIn a tank, a 4cm thick layer of water `(mu=4/3)` floats on a 6 cm thick layer of an organic liquid (`mu` = 1.5). Viewing at normal incidence, how far below the water surface does the bottom of tank appear to be?
View SolutionAn object is placed in front of a slab (`mu` = 1.5) pfthickness 6 cm at a distance 28 cm from it Other face of the slab is silvered. Find the position of final image.

View SolutionAn observer can see through a pinhole the top end of a thin rod of height h, placed as shown in figure. The beaker height 3h and its radius h. When the beaker is filled with a liquid upto a height 2h, he can see the lower end of the rod. Find the refractiveindex of the liquid.

View SolutionA person looking through a telescope focuses the lens at a point on the edge of the bottom of an empty cylindrical vessel Next he fills the entire vessel with a liquid of refractive index `mu`, without disturbing the telescope. Now, he observes the midpoint of the bottom of the vessel Determine the radius to depth ratio of the vessel
View SolutionA diverging beam of light from a point source S having divergence angle `alpha` falls symmetrically on a glass slab as shown. The angles of incidence of the two extreme rays are equal If the thickness of the glass slab is t and its refractive index is n, then the divergence angle of the emergent beam is

View SolutionAn observer looks at an object kept at a distance 30 cm in air. If a rectangular glass plate (`mu` =1.5) is placed between the observer and the object with its thick-ness along the line of observation, the object appears to the observer to be at a distance 25 cm. Find the thickness of glass plate. Position of the glass plate is now shifted (i) from object towards observers (ii) from observer towards the object How does it change the apparent position of the object as seen by the observer?
View SolutionAn air bubble is trapped inside a glass cube of edge 30 cm. Looking through the faceABEH, the bubble appears to be at normal distance 12 cm from this face and when seen from the opposite face CDGF, it appaears to be at normal distance 8 cm from CDGF. Find refractive index of glass and also the actual position of the bubble

View SolutionA parallel sides glass slab of thickness 4 cm is made of a material of refractive index `sqrt3`. When light is incident on one of the parallelfaces at an angle of `60^(@)` , it emerges from the other parallel face. Find the lateral displacement of the emergent beam.
View SolutionA ray of light travelling in a rarer medium strikes a plane bouhdary between the rarer medium and a denser medium at an angle of incidence ‘i’ such that the reflected and the refracted rays are mutually perpendicular. Another ray of light of same frequency is incident on the same boundary from the side of denser medium. Find the minimum angle of incidence at the denser-rarer boundary so that the second ray is totally reflected.

View SolutionA ray of light travelling in a transparent medium falls on a surface separating the medium from air at an angle of incidence of `45^(@)`. The ray undergoes total internal reflection. If n is the refractive index of the medium with respect to air, select the possible value of n from the following.
View SolutionA liquid of refractive index 1.5 is poured into a cyclindrical jar of radius 20 cm upto a height of 20 cm. A small bulb at the centre of bottom glowing. Find area of the liquid surface through which the light of the bulb passes into air.
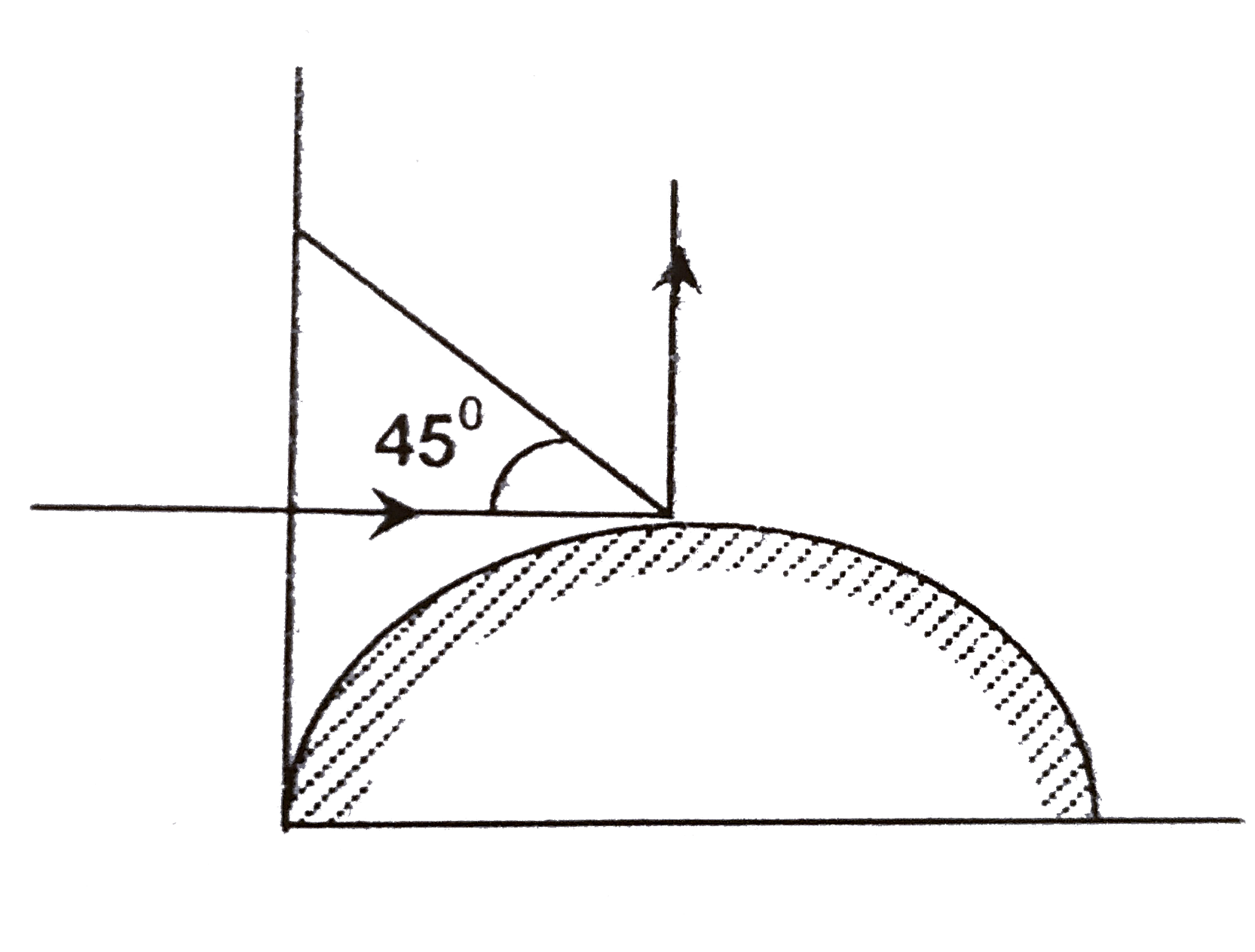
View Solution(a) Fig. shows a cross-section of a 'light pipe' made of a glass fibre of refractive index `1.68`. The outer covering of the pipe is made of a material of refractive index `1.44`. What is the axis of the pipe for which total reflection inside the pipe take place as shwon.
(b) What is the answer if there is no outer covering if the pipe ?
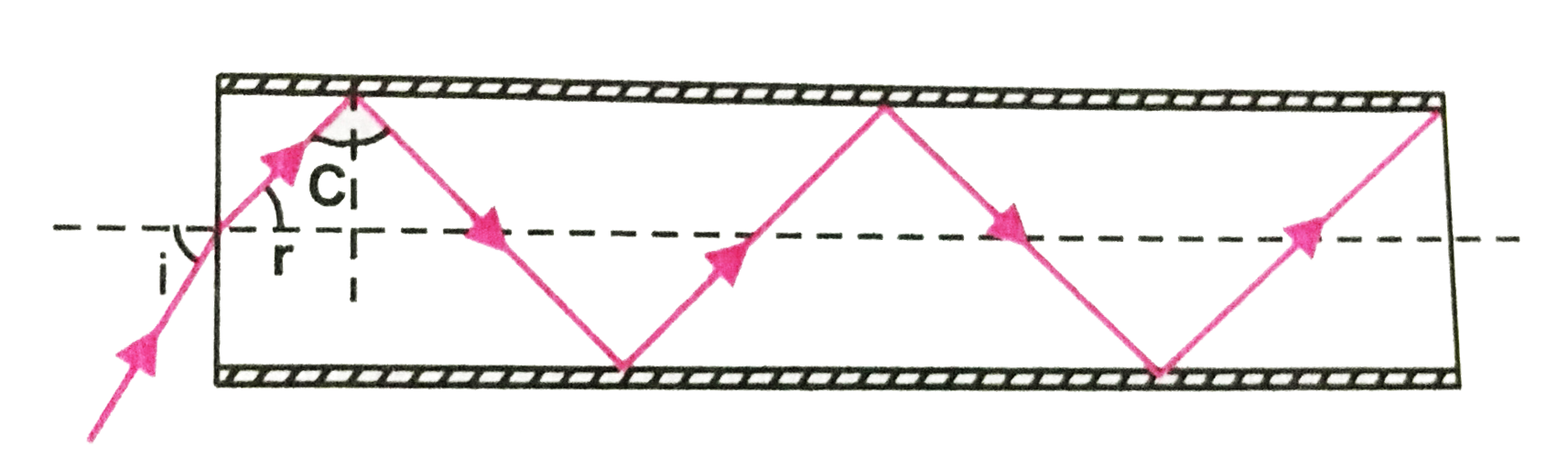
View SolutionLight is incident at an angle `alpha` on one planar end of a transparent cylindrical rod of refractive index `mu`. Determine the least value of `mu` so that the light entering the rod does not emerge from the curved surface of rod irrespective of the value of `alpha` `
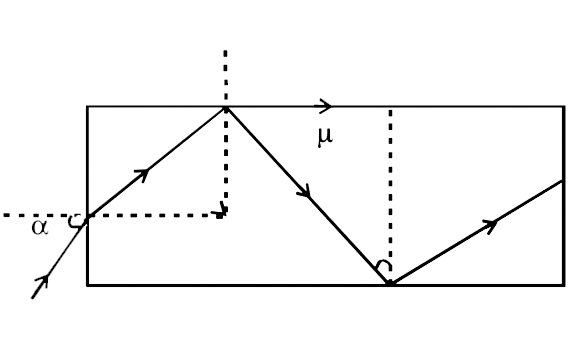
View SolutionA rectangular glass slab ABCD of refractive index `n_(1)` is immersed in water of refractive index `n_(2) (n_(1) gt n_(2) )`. A ray of light is incident at the surface AB of the slab as shown. The maximum value of the angle of incidence `a_(max)` .such that the ray comes out only from the other surface CD, is given by

View SolutionWhat will be the minimum angle of incidence such that the total internal reflection occurs on both the surfaces?

View SolutionA ray of light incident on the horizontal surface of a glass slab at an angle of incidence ‘i’just grazes the adjacent vertical surface after reflection. Compute the critical angle and refractive index of glass
View SolutionLight is incident normally on face AB of a prism as shown in figure. A liquid of refractive index p is placed on face AC of the prism. The prism is made of glass of refractive index 3/2. The limits of p for which total internal reflection takes place on face AC is

View SolutionWhat is the value of the refractive index for a `90^(@)- 45^(@) 45^(@)` prism which is used to deviate a beam through `90^(@)` by total internal

View SolutionA beam of light consisting of red, green and blue colours is incident on a right angle prism. The refractive indices of the material of the prism for the red, green and blue wavelengths are 1.39, 1.44 and 1.47 respectively. The colour of light that comes out of the prism is

View SolutionWhite light is incident on the interface of glass and air as shown in the figure. If green light is just totally internally reflected then the emerging ray in air contains:

View SolutionA rectangular block of glass is placed on a printed page lying on a horizontal surface. Find the minimum value of the refractive index of glass for which the letters on the page are not visible from any of the vertical faces of the block.

View SolutionA plane mirror is placed at the bottom of a tank containing a liquid of refractive index `mu`. P is a small object at a heigth h above the mirror. An observer O, vertically above P, outside the liquid, observes P and its image in the mirror. The apparent

View SolutionA cubic container is filled with a liquid whose refractive index increases linearly from top to bottom. Which of the following represents the path of a ray of light inside the liquid ?

View SolutionA light ray travelling in a glass medium is incident on glass - air interface at an angle of incidence Q. The reflected (R) and transmitted (T) intensities, both as function of 0, are plotted. The correct sketch is

View SolutionFind the variation of Refractive index assuming it to be a function of y such that a ray entering origin at grazing incident follows a parabolic path `y=x^(2)` as shown in

View SolutionA ray of light is incident on a glass slab at grazing incidence. The refractive index of the material of the slab is given by `mu =sqrt(1+sqrty) `. If the thickness of the slab is d, determine the equation ofthe trajectory of the ray inside the slab and the coordinates of the point where the ray exits from the slab. Take the origin to be at the point of entry of the ray.
View SolutionDue to a vertical temperature gradient in the atmosphere, the index of refraction varies. Suppose index of refraction varies as
n =`n_(0)sqrt(1+ay)`, where `n_(0)` is the index of refraction at the surface and ‘a’=`2.0xxl0^(-6)“m^(-1)`. A person of height h= 2.0 m stands on a level surface. Beyond what distacne will he not see the run way?

View SolutionThe refraction index of an anisotropic medium varies as p =`mu=mu_(0)sqrt((x+1))` , where 0 `lt=` x `lt =`a. A ray of light is incident at the origin just along y-axis (shown in figure). Find the equation of ray in the medium.

View SolutionA vessel of depth 2d cm is half filled with a liquid of refractive index `mu_(1)` and the upper half with a liquid of refractive index `mu_(2)`. The apparent depth of the vessel seen perpendicularly is
View SolutionA ray of ligth enters into a glass slab from air as shown in fig.2.65. If refractive index of glass slab is given by `mu` = A — Bt where A and B are constants and ‘t’ is the thickness of slab measured from the top surface. Find the maximum depth travelled by ray in the slab. Assume thickness of slab to be sufficiently large

View SolutionA ray of light travelling in air is incident at a grazing angle on a large transparent slab of thickness t = 2.0m. The point of incidence is the origin.
The medium has a variable refractive index(y) given by `mu(y)=sqrt(ky+1)`
Where y is in m and k = 0.25`m^(-1)`
Express a relation between the angle of incidence and the slope of the trajectory m, in terms of the refractive index at that point `mu` (y)

View SolutionA small object stuck on the surface of a glass sphere `(n=1.5)` is viewed from the diametrically opposite position. Find transverse magnification.
View SolutionA solid glass sphere with radius R and an index of refraction `1.5` is silvered over one hemisphere. A small object is located on the axis of the sphere at a distance 2R to the left of the vertex of the unsilvered hemisphere. Find the position of final image after all refractions and reflection have taken place.
View SolutionA point object is placed at the centre of a glass sphere of radius 6cm and refractive index 1.5. The distance of virtual image from the surface is
View SolutionAn air bubble in glass (`mu` = 1.5) is situated at a distance 3 cm from a convex surface of diameter 10 cm as shown in figure. At what distance from the surface will the bubble appear?

View SolutionOne end of a cylindrical glass (`mu` = 1.5) is given the shape of a concave refracting surface of radius 10 cm. An air bubble is situated in the glass rod at a point on its axis such that it appears to be at distance 10 cm from the surface and inside glass when seen from the other medium. Find the actual location of air bubble.
View SolutionA transparent thin film of uniform thickness and refractive index `n_(1)` =1.4 is coated on the convex spherical surface of radius R at one end of a long solid glass cylinder of refractive index `n_(2)` = 1.5, as shown in figure. Rays of light parallel to the axis of the cylinder traversing through the film from air to glass get focused at distance f] from the film, while rays of light traversing from glass to air getfocused at distacnce f2 from the film. Then, the magnitudes of `f_(1),f_(2)` are

View SolutionA spherical solid glass paper weight of diameter 6 cm has a small air bubble at a distance of 1.5 cm from the centre. If the air bubble be viewed from the side to which it is nearest along the line joining the bubble and the centre, find where will it appear.
View SolutionA biconvex lens of focal length 15 cm is in front of a plane mirror. The distance between the lens and the mirror is 10 cm. A small object is kept at a distance of 30 cm from the lens. The final image is
View SolutionA bi-convex lens is formed with two thin plano-convex lenses as shown in the figure. Refractive index ‘n ’ of the first lens is 1.5 and that of the second lens is 1.2. Both the curved surface are of the same radius of curvature R=14 cm. For this bi-convex lens, for an object distance of 40 cm, the image distance will be

View SolutionAn object is `5.0 m` to the left of a flat screen. A converging lens for which the focal length is `f=0.8 m` is placed between object and screen.
(a) Show that two lens positions exist that form images on the screen and deremine how far these positions are from the object?
(b) How do the two images differ from each other?
View SolutionA point object is placed at a distance of `12 cm` from a convex lens of focal length `10 cm.` On the other side of the lens, a convex mirror is placed at a distance of `10 cm` from the lens such that the image formed by the combination coincides with the object itself. The focal length of the convex mirror is
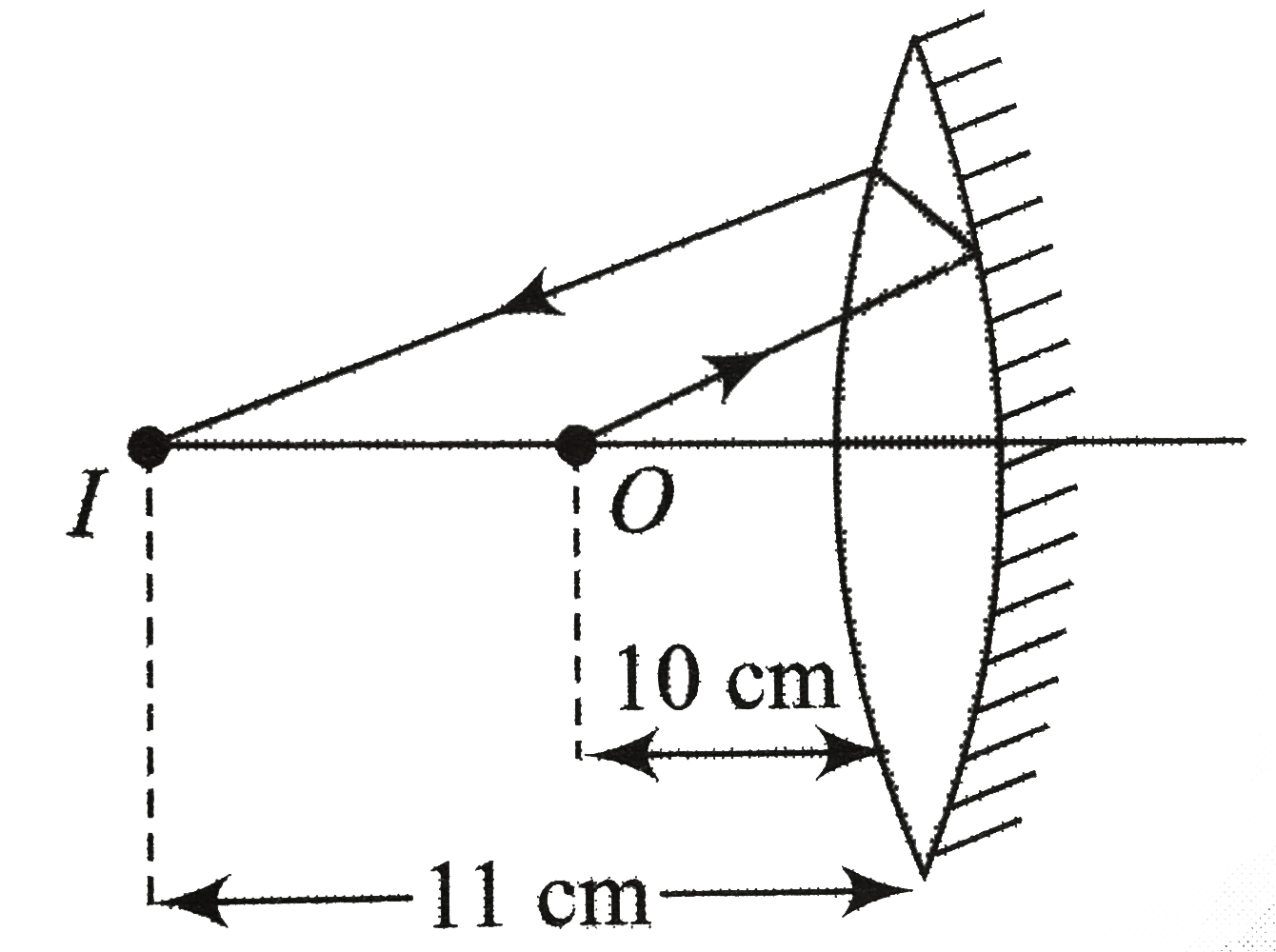
View SolutionA pin is placed 10cm in front of a convex lens of focal length 20cm, made of a material having refractive index 1.5 . The surface of lens farther away from the pin is silvered and has a radius of curvature 22cm. Determine the position of the final image. Is the image real or virtual?
View SolutionA biconvex thin lens is prepared from glass of refractive index `3//2.` The two bounding surfaces have equal radii of `25cm` each. One of the surfaces is silvered from outside to make it reflecting. Where should an object be placed before this lens so that the image coincides with the object.
View SolutionWhat is the refractive index of material of a plano-convex lens, if the radius of curvature of the convex surface is 10 cm and focal length of the lens is 30 cm ?
View SolutionA concave lens of glass, refractive index 1.5 has both surfaces of same radius of curvature R. On immersion in a medium of refractive index 1.75, it will behave as a
View SolutionA hollow convex lens of glass will behave like a
View SolutionThe diagram shows a concavo - convex lens. What is the condition on the refractive indices so that the lens is diverging?
The refractive index of the lens is `mu_(2)`

View SolutionThe magnification of an object placed it front of a convex lens of focal length `20cm` is `+2`. To obtain a magnification of `-2` , the object will has to be moved a distance equal to
View SolutionTwo point sources `S_(1)` and `S_(2)` are 24 cm apart. What should a convex lens of focal length 9 cm be placed between them so that the images of both sources formed at the same place ?
View SolutionAn object is placed at `A(OA gt f)`. Here, f is the focal length of the lens. The image is formed at B. A perpendicular is erected at O and C is chosen such that `/_BCA = 90^(@)`. Let OA = a, OB = b and OC = c. Then the value of f is
View SolutionA magnifying lens has a focal length of 10 cm. (a) Where should the object be placed if the image is to be 30 cm from the lens ? (b) What will be the magnification ?
View SolutionIn the figure, light is incident on the thin lens as shown. The radius of curvature for both the surface is R. Determine the focal length of this system.

View SolutionThe linear magnification of an object placed on the principal axis of a convex lens offocal length 30cm is found to be +2. In order to obtain a magnification of -2, by how much distance should the object be moved?
View SolutionThe distance between the object and the real image formed by a convex lens is d. If the linear magnification is m, find the focal length of the lens in terms of d and m.
View SolutionA concave lens of focal length f forms an image which is n times the size of the object What is the distance of the object from the lens in terms of f and n?
View SolutionA glass convex lens of refractive index `3/2` has got a focal length equal to 0.3 m. Find the focal length of the lens if it is immersed in water of refractive index` 4//3`.
View SolutionAs shown in figure a spherical air lens of radii `R_(1)=R_(2)`= 10cm is cut in a glass (`mu`= 1.5) cylinder. Determine the focal length and nature of air lens. If a liquid of refractive index 2 is filled in the lens, what will happen to its focal length and nature?

View SolutionA point object O is placed at a . distance of 30 cm from a convex lens of focal length 20cm cut into two halves each of which is displaced by 0.05cm as shown in figure. Find the position of the image? If more than one image is formed, find their number and distance between them?

View Solution
ILLUSTRATION questions and complete solutions for chapter RAY OPTICS AND OPTICAL INSTRAUMENTS of NARAYANA PHYSICS (HINGLISH) of Class 12
All Exercises from NARAYANA Class 12 PHYSICS RAY OPTICS AND OPTICAL INSTRAUMENTS
- CUQ (ASSERTION & REASON)
- CUQ (DEFECTS OF EYE)
- CUQ (DISPERSION)
- CUQ (LENS MAKER’S FORMULA)
- CUQ (OPTICAL INSTRUMENTS : TELESCOPES)
- CUQ (OPTICAL INSTRUMENTS MICROSCOPES)
- CUQ (PRISM)
- CUQ (REFLECTION)
- CUQ (REFRECTION)
- EXERCISE - 1 (C.W)(DEFECTS OF THE EYE)
- EXERCISE - 1 (C.W)(DISPERSION BY A PRISM)
- EXERCISE - 1 (C.W)(LENSES)
- EXERCISE - 1 (C.W)(REFLECTION)
- EXERCISE - 1 (C.W)(REFRACTION THROUGH PRISM)
- EXERCISE - 1 (C.W)(REFRACTION THROUGH SPHERICAL SURFACES)
- EXERCISE - 1 (C.W)(REFRACTION)
- EXERCISE - 1 (C.W)[OPTICAL INSTRUMENTS ( MICROSCOPES )]
- EXERCISE - 1 (C.W)[OPTICAL INSTRUMENTS ( TELESCOPES )]
- EXERCISE- 3
- EXERCISE- 4
- EXERCISE- 4 One or more than one correct answer type
- EXERCISE-1 (H.W)( DEFECTS OF THE EYE )
- EXERCISE-1 (H.W)( DISPERSION BY A PRISM )
- EXERCISE-1 (H.W)( LENSES )
- EXERCISE-1 (H.W)( OPTICAL INSTRUMENTS( MICROSCOPES ) )
- EXERCISE-1 (H.W)( OPTICAL INSTRUMENTS( TELESCOPES ) )
- EXERCISE-1 (H.W)( REFLECTION )
- EXERCISE-1 (H.W)( REFRACTION )
- EXERCISE-1 (H.W)( REFRACTION THROUGH PRISM )
- EXERCISE-1 (H.W)( REFRACTION THROUGH SPHERICAL SURFACES )
- EXERCISE-2 (C.W)( DEFECTS OF THE EYE )
- EXERCISE-2 (C.W)( OPTICAL INSTRUMENTS (MICROSCOPES) )
- EXERCISE-2 (C.W)( OPTICAL INSTRUMENTS (TELESCOPES) )
- EXERCISE-2 (C.W)(DISPERSION BY A PRISM )
- EXERCISE-2 (C.W)(REFLECTION)
- EXERCISE-2 (C.W)(REFRACTION THROUGH A PRISM )
- EXERCISE-2 (C.W)(REFRACTION THROUGH SPHERICAL SURFACES )
- EXERCISE-2 (C.W)(REFRACTION)
- EXERCISE-2 (H.W)(DEFECTS OF THE EYE)
- EXERCISE-2 (H.W)(DISPERSION BY A PRISM)
- EXERCISE-2 (H.W)(LENSES & THEIR COMBINATIONS)
- EXERCISE-2 (H.W)(OPTICAL INSTRUMENTS ( MICROSCOPES ))
- EXERCISE-2 (H.W)(OPTICAL INSTRUMENTS ( TELESCOPES ))
- EXERCISE-2 (H.W)(REFLECTION)
- EXERCISE-2 (H.W)(REFRACTION THROUGH A PRISM)
- EXERCISE-2 (H.W)(REFRACTION THROUGH SPHERICAL SURFACES)
- EXERCISE-2 (H.W)(REFRACTION)
- ILLUSTRATION