Complete Solutions to EXAMPLE of chapter AREA OF PARALLELOGRAMS AND TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | AREA OF PARALLELOGRAMS AND TRIANGLES |
| MODERN PUBLICATION | EXAMPLE |
| Number Of Questions | 95 |
| Academic Year | 2023-24 |
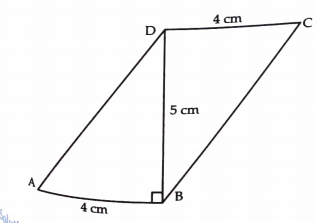
ABCD is a quadrilateral and BD is one of its diagonals as shown in the figure. Prove that ABCD is a parallelogram and find its area.
View SolutionShow that the line segments joining the mid-points of opposite sides of a quadrilateral bisect each other.
View SolutionProve that, of all the parallelograms of given sides, the parallelogram, which is recatangle has the greatest area.
View SolutionShow that a median of a triangle divides it into two triangles of equal areas.
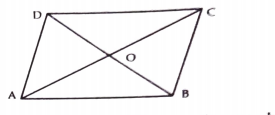
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area.
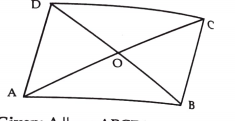
View SolutionIf each diagonal of a quadrilateral separated it into two triangles of equal area, then show that quadrilateral is a parallelogram.
View SolutionProve that the are of the rhombus is half the product of the lengths of its diagonals.
View SolutionIn a quadrilateral ABCD, AO and BO are bisectors of `angleA` and angle B respectively. Prove that
`angleAOB=1/2(angleC+angleD)`
View SolutionIn the figure. It is given that AD||BC. Proe that are `ar(triangleCOD)=ar(triangleABO)`
View SolutionD, E and F are respectively the mid-points of the sides BC, CA and AB of a `triangle ABC`. Show that:- BDEF is a parallelogram.
View SolutionD,E and F are mid-points of the sides BC, CA and AB respectively of `triangleABC`. Prove that
`ar(triangleDEF) = 1/4 ar (triangleABC)`
View SolutionD,E and F are mid-points of the sides BC, CA and AB respectively of `triangleABC`. Prove that
`ar(||gmBDEF)= 1/2 ar (triangleABC)`
View SolutionIn the figure. ABCD is a parallelogram and O is any point on BC . Prove that `ar (triangleABO) + ar (triangleDOC) = ar(triangleODA)`
View SolutionTriangle ABC and DBC are on the same base BC with A,D on opposite sides of line BC, such that `ar(triangleABC) = ar(triangleDBC)`. Prove that BC bisects AD.
View SolutionABCD is trapezium in which AB||DC . DC is produced to E such that CE = AB, prove that `ar(triangleABD) = ar(triangleBCE)`
View SolutionProve that the area of an equilateral triangle `(sqrt3)/(4)a^2`, where 'a' is the side of te triangle.
View SolutionIn the quadrilateral ABCD, it is given that L is the mid-point of AC. Prove that `arc(qud.ABLD)=ar(quad.DLBC)`
View SolutionP and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar (APB) = ar (BQC).
View SolutionABCD is a parallelogram and a line through A meets DC at P and BC (produced) at Q. Prove that `ar(triangleBPC) = ar(triangleDPQ)`
View SolutionABC is a triangle in which D is the mid-point of BC and E is the mid-point of AD. Prove that: `ar(triangleBED) = 1/4 ar(triangleABC)`
View SolutionABCD is parallelogram. X and Y are the mid-points of BC and CD respectively. Prove that ar `(DeltaAXY) =3/8` ar `(||)^(gm) ABCD`.
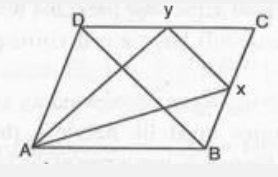
View SolutionP,Q,R and S are the mid-poins of the sides AB,BC,CD and DA respectively of quad. ABCD. Show that PQRS is a parallelogram such that `ar(||gmPQRS) = 1/2 ar(quad.ABCD)`
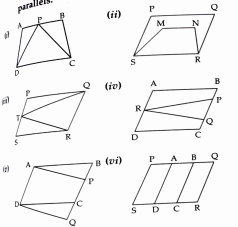
View SolutionWhich of the following figures lie on the same base and between the same parallels. Insuch a case, write the common base and the two parallels.
View SolutionABCD is a parallelogram, `AE bot DC` and `CF bot AD`. If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD.
View SolutionIf E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that ar(EFGH)`=1/2`ar(ABCD).
View SolutionP and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar (APB) = ar (BQC).
View SolutionIn Fig.
 , P is a point in the interior of a parallelogram ABCD. Show that `ar(APB)+ar(PCD)=1/2ar(ABCD)`.
, P is a point in the interior of a parallelogram ABCD. Show that `ar(APB)+ar(PCD)=1/2ar(ABCD)`.
View SolutionIn Fig.
 , P is a point in the interior of a parallelogram ABCD. Show that `ar(APD)+ar(PBC)=ar(APB)+ar(PCD)`.
, P is a point in the interior of a parallelogram ABCD. Show that `ar(APD)+ar(PBC)=ar(APB)+ar(PCD)`.
View SolutionIn fig.
 PQRS and ABRS are parallelograms and X is any point on side BR. Show that `ar(PQRS)=ar(ABRS)`.
PQRS and ABRS are parallelograms and X is any point on side BR. Show that `ar(PQRS)=ar(ABRS)`.
View SolutionIn fig.
 PQRS and ABRS are parallelograms and X is any point on side BR. Show that `ar(AXS)=1/2ar(PQRS)`.
PQRS and ABRS are parallelograms and X is any point on side BR. Show that `ar(AXS)=1/2ar(PQRS)`.
View SolutionA farmer was having a field in the form of a parallelogram PQRS. She took any point A on RS and joined it to points P and Q.In how many parts the field is divided ? What are the shapes of these parts ? The farmer wants to sow wheat and pulses in equal portions of the field separately. How should she do it ?
View SolutionE is any point on median AD of a `triangle ABC` . Show that ar (ABE) = ar (ACE).
View SolutionABC is a triangle in which D is the mid-point of BC and E is the mid-point of AD. Prove that: `ar(triangleBED) = 1/4 ar(triangleABC)`
View SolutionA diagonal of parallelogram divides it into four triangles of equal area.
View SolutionD, E and F are respectively the mid-points of the sides BC, CA and AB of a `triangle ABC`. Show that:- BDEF is a parallelogram.
View SolutionIf D, E, f are the mid-point of the sides of triangle ABC, prove that : `ar(/_\DEF)=1/4 ar(/_\ABC)`.
View SolutionD, E and F are respectively the mid-points of the sides BC, CA and AB of a `triangle ABC`. Show that:- BDEF is a parallelogram.
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD) = ar (BOC). Prove that ABCD is a trapezium.
View SolutionDiagonals AC and BD of quadrilateral ABCD interset at O such that OB = OD , If AB = Cd, then show that : `ar(DCB) = ar(ACB)`
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD) = ar (BOC). Prove that ABCD is a trapezium.
View SolutionD and E are points on sides AB and AC respectively of `DeltaABC` such that ar (DBC) = ar (EBC). Prove that `DE II BC`.
View SolutionXY is a line parallel to side BC of triangle ABC. If `BE II AC` and `CF II AB` meet XY at E and F respectively,show that ar (ABE) = ar (ACF).
View SolutionThe sides AB of parallelogram ABCD produced to any point P. A line through A and parallel to CP meets CB produced at Q and the parallelogram PBQR is completed
 Show that ar(ABCD) = ar(PBQR)
Show that ar(ABCD) = ar(PBQR)
View SolutionIn the figure. ABCD in a trapezium in which AB||DC. Proe that `ar(triangleAOD) = ar(triangleBOC)`
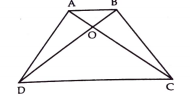
View Solution
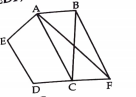 ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that:
ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that:
ar(ACB) = ar(ACF)
View Solution
 ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that:
ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that:
ar(AEDF) = ar(ABCDE)
View SolutionABCD is a trapezium with AB || DC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar (ADX) = ar (ACY). [Hint : Join CX.]
View SolutionAP||BQ||CR. Prove that ar(AQC) = ar(PBR)
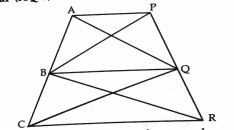
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD) = ar (BOC). Prove that ABCD is a trapezium.
View Solution
 ar(DRC) = ar(DPC) and ar(BDP) = ar(ARC). Show that both the quadrilaterals ABCD and DCPR are trapeziums.
ar(DRC) = ar(DPC) and ar(BDP) = ar(ARC). Show that both the quadrilaterals ABCD and DCPR are trapeziums.
View SolutionParallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
View Solution
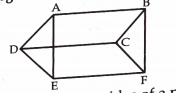 ABCD, DCFE and ABFE are parallelograms. Show that ar(ADE) = ar(BCF)
ABCD, DCFE and ABFE are parallelograms. Show that ar(ADE) = ar(BCF)
View SolutionABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that: ar(BPC) = ar(DPQ)
View Solution
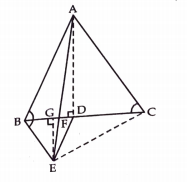
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE interesects BC at F, show that :
ar(BDE) = `1/4` ar(ABC)
View Solution
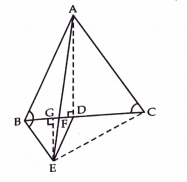
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE interesects BC at F, show that :
ar(BDE) = `1/2`ar(BAE)`
View Solution
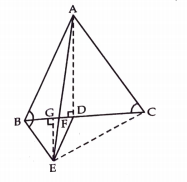
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE interesects BC at F, show that :
ar(ABC) = 2ar(BEC)
View Solution
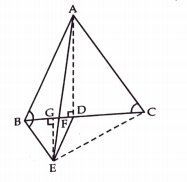
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE interesects BC at F, show that :
ar(BFE) = ar(AFD)
View Solution
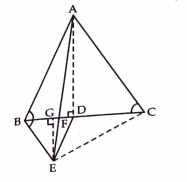
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE interesects BC at F, show that :
ar(BFE) = 2ar(FED)
View Solution
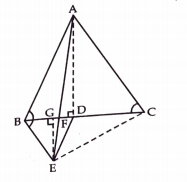
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE interesects BC at F, show that :
ar(FED) = `1/8`ar(AFC)
View SolutionDiagonals AC and BD of quadrilateral ABCD intersect each other at P. Show that ar `(APB) xx ar (CPD)` = ar `(APD)xx ar(BPC)`.
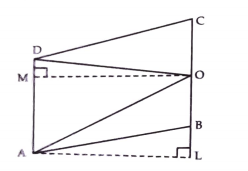
View SolutionP and Q are respectively the midpoints of sides AB and BC or a triangle ABC and R is the mid-point of AP, show ar(PRQ)=`1/2` ar(ARC).
View SolutionP and Q are respectively the midpoints of sides AB and BC or a triangle ABC and R is the mid-point of AP, show ar(RQC) = `3/8` ar(ABC).
View SolutionP and Q are respectively the midpoints of sides AB and BC or a triangle ABC and R is the mid-point of AP, show ar(PBQ)=ar(ARC).
View Solution
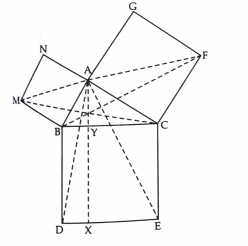 ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segent AX `bot` DE meets BC at Y. Show that:
ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segent AX `bot` DE meets BC at Y. Show that:
`triangleMBC congtriangleABD`
View Solution
 ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segent AX `bot` DE meets BC at Y. Show that:
ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segent AX `bot` DE meets BC at Y. Show that:
ar(BYXD) =2ar(MBC)
View Solution
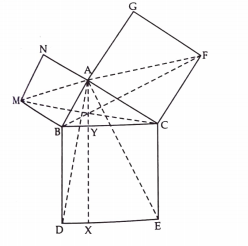 ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segent AX `bot` DE meets BC at Y. Show that:
ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segent AX `bot` DE meets BC at Y. Show that:
ar(BYXD) = ar(ABMN)
View Solution
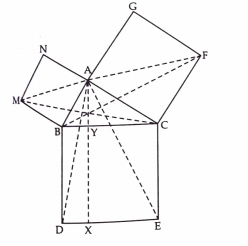 ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segent AX `bot` DE meets BC at Y. Show that:
ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segent AX `bot` DE meets BC at Y. Show that:
`triangleFCB congtriangleACE`
View Solution
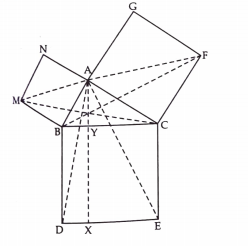 ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segent AX `bot` DE meets BC at Y. Show that:
ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segent AX `bot` DE meets BC at Y. Show that:
ar(CYXE) = 2ar(FCB)
View Solution
 ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segent AX `bot` DE meets BC at Y. Show that:
ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segent AX `bot` DE meets BC at Y. Show that:
ar(CYXE) = ar(ACFG)
View Solution
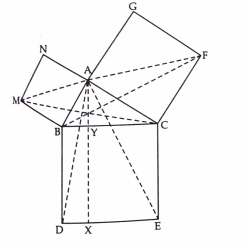 ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segent AX `bot` DE meets BC at Y. Show that:
ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segent AX `bot` DE meets BC at Y. Show that:
ar(BCED) = ar(ABMN) + ar (ACFG)
View SolutionABCD is a parallelogram and X is the mid-point of AB. If ar (AXCD) = `24 cm^2`, then ar (ABC) = `24 cm^2`.
View SolutionPQRS is a rectangle inscribed in a quadrant of a circle of radius 13 cm. A is any point on PQ. If PS = 5 cm, then ar (PAS) = `30 cm^2`.
View SolutionPQRS is a parallelogram whose area is `180 cm^2` and A is any point on the diagonal QS. The area of `DeltaASR = 90 cm^2`.
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then ar (BDE)=`1/4` ar(ABC).
View SolutionIn the figure
 ABCD and EFGD are two parallelograms and G is the mid-point of CD. Then ar(DPC) = `1/2` ar(EFGD)
ABCD and EFGD are two parallelograms and G is the mid-point of CD. Then ar(DPC) = `1/2` ar(EFGD)
View SolutionIn the figure
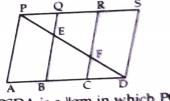 PSDA is a parallelogram. Points Q and R are taken on PS such that PQ = QR = RS and PA||QB||RC. Prove that: `ar(trianglePQE) = ar(triangleCFD)`
PSDA is a parallelogram. Points Q and R are taken on PS such that PQ = QR = RS and PA||QB||RC. Prove that: `ar(trianglePQE) = ar(triangleCFD)`
View SolutionX and Y are points on the side LN of the triangle LMN such that LX = XY = YN. Through X, a line is drwan parallel to LM to meet MN at Z. Prove that are (LZY) = ar(MZYX)
View SolutionThe area of the parallelogram ABCD is `90 cm^2`
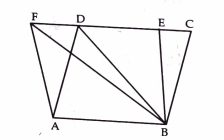
Find ar(ABEF)
View SolutionThe area of the parallelogram ABCD is `90 cm^2`

Find ar(ABD)
View SolutionThe area of the parallelogram ABCD is `90 cm^2`
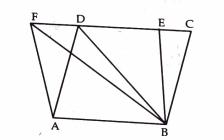
Find ar(BEF)
View SolutionIn `triangleABC,D` is the mid-point of AB and P is point on BC. If CQ||PD meets AB in Q then prove that :
`ar(BPQ) = 1/2 ar(ABC)`
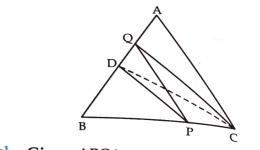
View SolutionABCD is a squre. E and F are respectivley the mid-points of BC and CD. If R is the mid-points of EF. Prove that ar (AER) = ar(AFR).
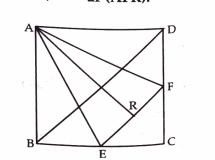
View SolutionO is any point on the diagonal PR of a parallelogram PQRS. Prove that : ar(PSO) = ar(PQO)

View SolutionABCD is a parallelogram in which BC is produced to E such that CE =BC.
 AE intersects CD at F. If ar(DFB) = `3cm^2`, find the area of the parallelogram ABCD.
AE intersects CD at F. If ar(DFB) = `3cm^2`, find the area of the parallelogram ABCD.
View SolutionIn trapezium ABCD, AB ||DC and L is the mid-point of BC. Through AL, a line PQ||AD has been drawn which meets AB at P and DC produced to Q. Prove that : ar(ABCD) = ar(APQD)
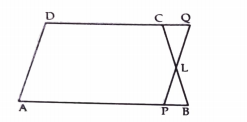
View SolutionIf the mid-point of the sides of a quadrilateral are joined in order, prove that the area of the parallelogram so formed will be half of the area of the given quadrilateral.
View SolutionA point is taken on the side BC of a parallelogram ABCD. AE and DC are produced to meet at F. Prove that : ar(ADF) = ar(ABFC)
View SolutionThe diagonals of a parallelogram ABCD intersect at a point O. Through O, a line is drawn to intersect AD at P and BC to Q. show that PQ divides the parallelogram into two parts of equal area.

View SolutionThe medians BE and CF of a triangle ABC interesct at G. Prove that the area of `triangleGBC `= area of the quadrilateral AFGE.
View SolutionIn the figure
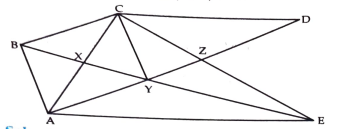 CD||AE and CYA||BA. Prove that : ar(CBX) = ar(AXY)
CD||AE and CYA||BA. Prove that : ar(CBX) = ar(AXY)
View SolutionABCD is a trapezium in which AB||DC, DC = 30 cm and AB = 50 cm. If X and Y are, respectivley that mid-points of AD and BC, prove that `ar(DCYX) = 7/9 ar(XYBA)`
View SolutionIn `triangleABC`, if L and M are the points on AB AC, respectivley such that LM||BC. Prove that ar(LOB) = ar(MOC)
View SolutionIn the figure
 ABCDE is any pentagon. BP drawn parallel to AC meets DC produced at P and EQ drawn parallel to AD meets CD produced at Q. Prove that : ar(ABCDE) = ar(APQ)
ABCDE is any pentagon. BP drawn parallel to AC meets DC produced at P and EQ drawn parallel to AD meets CD produced at Q. Prove that : ar(ABCDE) = ar(APQ)
View SolutionIf the medians of a `triangleABC` intersect at G, show that `ar(AGB) = ar(AGC) = ar(BGC) = `1/3`ar(ABC)
View SolutionIn the figure
 X and Y are the mid-points of AC and AB respectivley, QP||BC and CYQ and BXP are striaght lines. Prove that ar(ABP) = ar(ACQ)
X and Y are the mid-points of AC and AB respectivley, QP||BC and CYQ and BXP are striaght lines. Prove that ar(ABP) = ar(ACQ)
View Solution
EXAMPLE questions and complete solutions for chapter AREA OF PARALLELOGRAMS AND TRIANGLES of MODERN PUBLICATION of Class 9