Complete Solutions to EXERCISE of chapter AREA OF PARALLELOGRAMS AND TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | AREA OF PARALLELOGRAMS AND TRIANGLES |
| MODERN PUBLICATION | EXERCISE |
| Number Of Questions | 83 |
| Academic Year | 2023-24 |
In the figure. Show that ABCD is a parallelogram.
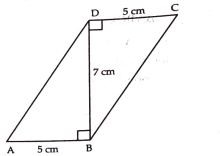 Calculate the area of ||gm ABCD.
Calculate the area of ||gm ABCD.
View SolutionFind the area of a rhombus whose diagonals are of lengths 10 cm and 8.2 cm.
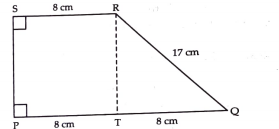
View SolutionCalculate the area of trap. PQRS, given in the figure.
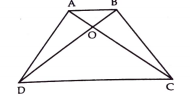
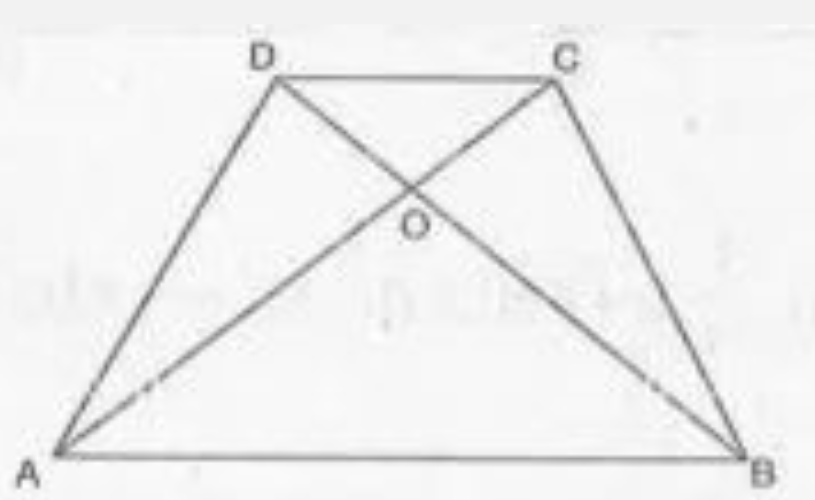
View SolutionIn the figure. ABCD in a trapezium in which AB||DC. Proe that `ar(triangleAOD) = ar(triangleBOC)`
View SolutionIn a quad. ABCD it is given that BD = 16 cm. If `AL bot BD` and `CM bot BD` such that AL = 9 cm and CM = 7 cm, then ar(quad. ABCD) = ?
View SolutionABCD is a parallelogram whose diagonals intersect at E. AC is produced to F such that CF = AE Prove that ar `(DeltaBDF)` = ar `(|| gm ABCD)`.
View SolutionABCD is a parallelogram whose diagonals intersect at E. AC is produced to F such that CF = AE Prove that ar `(DeltaBDF)` = ar `(|| gm ABCD)`.
View SolutionP and Q are respectively the midpoints of sides AB and BC or a triangle ABC and R is the mid-point of AP, show ar(PBQ)=ar(ARC).
View SolutionP and Q are respectively the midpoints of sides AB and BC or a triangle ABC and R is the mid-point of AP, show ar(PRQ)=`1/2` ar(ARC).
View SolutionP and Q are respectively the midpoints of sides AB and BC or a triangle ABC and R is the mid-point of AP, show ar(RQC) = `3/8` ar(ABC).
View SolutionIn fig. ABCD and AEFG are two parallelograms. If `angleC=55^@` and determine `angleF`
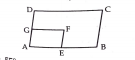
View SolutionABCD and AEFD are two parallelograms Prove that:
`ar(triangleAPE) : ar(trianglePFA) = ar(triangleQFD): ar(triangle PFD)`
View SolutionIn Fig.
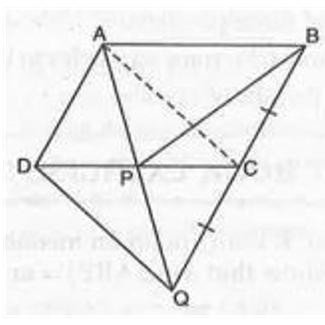
ABCD is a parallelogram. Prove that ar `(DeltaACP)` = ar `(DeltaDPQ)`.
View SolutionIn `triangleABC`, it L and M are points on AB and AC respectively such that LM||BC. Prove that :
`ar(triangleLCM) = ar(triangleLBM)`
View SolutionIn `triangleABC`, it L and M are points on AB and AC respectively such that LM||BC. Prove that :
`ar(triangleLBC) = ar(triangleMBC)`
View SolutionD and E are points on sides AB and AC respectively of `DeltaABC` such that ar (DBC) = ar (EBC). Prove that `DE II BC`.
View SolutionD and E are points on sides AB and AC respectively of `DeltaABC` such that ar (DBC) = ar (EBC). Prove that `DE II BC`.
View SolutionABCD is parallelogram. X and Y are the mid-points of BC and CD respectively. Prove that ar `(DeltaAXY) =3/8` ar `(||)^(gm) ABCD`.
View SolutionPQRS and PABC are two parallelograms of equal area. Prove that `QC||BR`
View SolutionTwo parallelograms ABCD and AEFB are drawn on opposite sides of AB. Prove that `ar(||gmABCD)` + `ar(||gmAEFB)` = `ar(||gm EFCD)`
View SolutionA man who had a plot in the shape of a parallelogram divided it into three equal parts and gave one-thrid part ot his son which again was in the shape of a parallelogram. The son seeing that there was no school in the village ecides to open a school there. Answer the following questions:
Show how could this decision of the man be implemented. What part did the son get? Explain with figure.
View SolutionA man who had a plot in the shape of a parallelogram divided it into three equal parts and gave one-third part to his son which again was in the shape of a parallelogram. The son seeing that there was no school in the village he decides to open a school there. Answer the following questions:
Was the son's decision right?
View SolutionA man who had a plot in the shape of a parallelogram divided it into three equal parts and gave one-third part to his son which again was in the shape of a parallelogram. The son seeing that there was no school in the village he decides to open a school there. Answer the following questions:
Was the son's decision right?
View SolutionIn a class, the teacher gave two simiar cardboard pieces which are in the shape of parallelogram to two groups. First group was asked find area of parallelogram,having AB as base. Another group was asked to find the height (h) of parallelogram having AD as base.
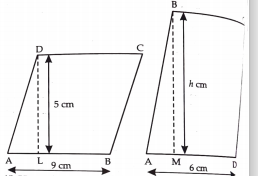 What values are depicted?
What values are depicted?
View SolutionIn a class, the teacher gave two simiar cardboard pieces which are in the shape of parallelogram to two groups. First group was asked find area of parallelogram,having AB as base. Another group was asked to find the height (h) of parallelogram having AD as base.
 What values are depicted?
What values are depicted?
View SolutionIf ar(||gm ABCD) = `252 cm^2`, then find the area of `triangleADB`?
View SolutionIn the figure.
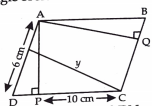
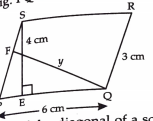 PQRS is a || gm. Find the value of y.
PQRS is a || gm. Find the value of y.
View SolutionIf the length of the diagonal of a square is 8 cm, then find its area.
View SolutionThe figure obtained by joining the midpoints of the adjacent sides of a rectangle of sides 8 cm and 6 cm is :
View SolutionIf the area of a parallelogram ABCD is `30cm^2`, then find the length of altitude AQ?
View SolutionIn the figure.
 ABCD is a ||gm and DN `bot` AB. If AB = 10 cm and DN = 4cm . Find ar(||gm ABCD) are ar`(triangleABD)`
ABCD is a ||gm and DN `bot` AB. If AB = 10 cm and DN = 4cm . Find ar(||gm ABCD) are ar`(triangleABD)`
View SolutionABCD is a rhombus AC = 8 cm, and DB = 6 cm. Find the length of BC.
View SolutionIf ABC and BDE are two equilateral triangles such that D is the mid-point of BC, then find `ar(triangleABC) : ar(triangleBDE)`
View SolutionP is any point on base BC of `triangleABC` and D is the mid-point of the BC. DE is drawn parallel to PA to meet AC at E. If `ar(triangleABC)= 12 cm^2`, then find area of `triangleEPC`
View SolutionPQRS is a rectangle inscribed in a quadrant of a circle of radius 13 cm. A is any point on PQ. If PS = 5 cm, then ar (PAS) = `30 cm^2`.
View SolutionTrue/False
Area of || gm= `1/2` base`xx` corresponding height.
View SolutionTrue/False
If the area of a || gm with one side 24 cm and corresponding height h cm is `192 cm^2`, then h = 16 cm.
View SolutionTrue/False
If the diagonals of a rhombus are 14 cm and 18 cm, then its area is `126 cm^2`
View SolutionParallelogram on equal bases and between the same parallels are equal in area.
View SolutionTrue/False
Two parallelograms are on the same base and between the same parallels. The ratio of their areas is 1:2.
View SolutionABCD is a parallelogram and X is the mid-point of AB. If ar (AXCD) = `24 cm^2`, then ar (ABC) = `24 cm^2`.
View SolutionTrue/False
If AD is the median of `triangleABC` and P is a point on AC such that `ar(triangleADP): ar (triangleABD) = 2:3`, then `ar(trianglePDC) : ar(triangleABC) =1:3`
View SolutionTrue/False
In a `triangleABC,D,E,F` are the mid-points of the sides BC,CA and AB respectively. If `ar(triangleABC) = 16cm^2`, then ar(trap FBCE) is `8cm^2`
View SolutionTrue/False
A,B,C,D are mid-points of sides of ||gm PQRS. If ar (PQRS) = `36cm^2`, then ar (ABCD) = `18cm^2`
View SolutionABCD s a trapezium in which AB||CD and AD=BC

Show that: `angleA=angleB`
View SolutionFill in the Blanks:
If `R_1 and R_2` are two congruent regions, then area of `R_1` is ______ are of `R_2`
View SolutionFill in the Blanks:
A diagonal of || gm divides it into two triangles of ________ area.
View SolutionFill in the Blanks:
Parallelogram on the _______ base and __________ the same parallels are equal in area.
View SolutionFill in the Blanks:
The area of || gm is equal to the product of any of its sides and ____________ altitude.
View SolutionFill in the Blanks:
Ratio of areas of a triangle and a ||gm sharing the same base and between the same paralleles is _________
View SolutionFill in the Blanks:
Area of triangle is _________ the product of any of its sides and corresponding altitude.
View SolutionFill in the Blanks:
Triangles with equal area and having any side of one equal to any side of the other have equal corresponding______
View SolutionA diagonal of parallelogram divides it into four triangles of equal area.
View SolutionShow that the line segments joining the mid-points of opposite sides of a quadrilateral bisect each other.
View SolutionFill in the Blanks:
The ratio of area of rectangle and a triangle sharing the same base and between the same _______ is 2:1
View SolutionThe median of a triangle divides it into two
View SolutionTwo parallelograms are on equal bases andbetween the same parallels. The ratio of their areas is
View SolutionThe median of a triangle divides it into two
View SolutionABCD is a parallelogram. P is any point on CD. If `ar(triangleDPA) = 15 cm^2 and ar(triangleAPC) = 20 cm^2`, the ar`(triangleAPB) = `
View SolutionThe figure obtained by joining the midpoints of the adjacent sides of a rectangle of sides 8 cm and 6 cm is :
View SolutionIn trapezium ABCD `AB||DC`. If ar (AOD) = `15 cm^2` then ar (BOC) is :
View SolutionThe lengths of the diagonals of a rhombus are 10 cm and 8.2 cm .Its area will be :
View SolutionIn a quad. ABCD it is given that BD = 16 cm. If `AL bot BD` and `CM bot BD` such that AL = 9 cm and CM = 7 cm, then ar(quad. ABCD) = ?
View SolutionIn a ||gm ABCD, if P and Q are mid-points of AB and CD respectively and ar(||gm ABCD) = `16 cm^2`, then ar(||gm APQD) = ?
View SolutionThe median of a triangle divides it into two
View SolutionThe mid-point of the sides of a triangle along with any of the vertices as the fourth point make a parallelogram of area equal to
View SolutionTwo parallelograms are on equal bases andbetween the same parallels. The ratio of their areas is
View SolutionABCD is a quadrilateral whose diagonal AC divides it into two parts, equal in area, then ABCD
View SolutionIf a triangle and a parallelogram are on the same base and between same parallels, then the ratio of the area of the triangle to the area of parallelogram is
View Solution`triangleABC~ trianglePQR`. If `ar(ABC) = 2.25 m^2. ar(PQR) = 6.25m^2,PQ = 0.5 m`, then length of AB is
View SolutionIf `triangleABC~triangleDEF`, BC = 4 cm, EF = 5 cm and ar`(triangleABC) = 80 cm^2`, then `ar(triangleDEF)`is
View SolutionThe area of two similar triangles ABC and PQR are `25 cm^2, 49cm^2`. If QR = 9.8 cm, then BC is
View SolutionWhat is the area of an equilateral triangle whose sides is 'a'?
View SolutionTick the correct answer and justify : Sides of two similar triangles are in the ratio 4:9. Areas of these triangles are in the ratio
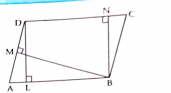
View SolutionIn the figure, find the area of ||gm.
View SolutionTwo parallelograms are on equal bases andbetween the same parallels. The ratio of their areas is
View SolutionIn figure.
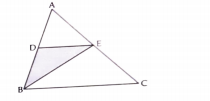 D and E are the mid-points o sides. AB, AC respectively of `triangleABC`. If `ar(triangleABC) = 256 cm^2`, then find `ar(triangleBDE)`
D and E are the mid-points o sides. AB, AC respectively of `triangleABC`. If `ar(triangleABC) = 256 cm^2`, then find `ar(triangleBDE)`
View SolutionABCD is a trapezium in which AB||DC, DC = 30 cm and AB = 50 cm. If X and Y are, respectivley that mid-points of AD and BC, prove that `ar(DCYX) = 7/9 ar(XYBA)`
View SolutionAP||BQ||CR. Prove that ar(AQC) = ar(PBR)
View SolutionABCD is parallelogram. X and Y are the mid-points of BC and CD respectively. Prove that ar `(DeltaAXY) =3/8` ar `(||)^(gm) ABCD`.

View SolutionIf the medians of a `triangleABC` intersect at G, show that `ar(AGB) = ar(AGC) = ar(BGC) = `1/3`ar(ABC)
View SolutionPQRS is a ||gm. L is any point on PS and M is any point on QR. Show that:
`ar(triangleQLR) = ar(triangleQPM) + ar(triangleSRM)`
View SolutionPQRS is a ||gm. L is any point on PS and M is any point on QR. Show that:
`ar(triangleQLR) = ar(triangleQPM) + ar(triangleSRM)`
View Solution
EXERCISE questions and complete solutions for chapter AREA OF PARALLELOGRAMS AND TRIANGLES of MODERN PUBLICATION of Class 9