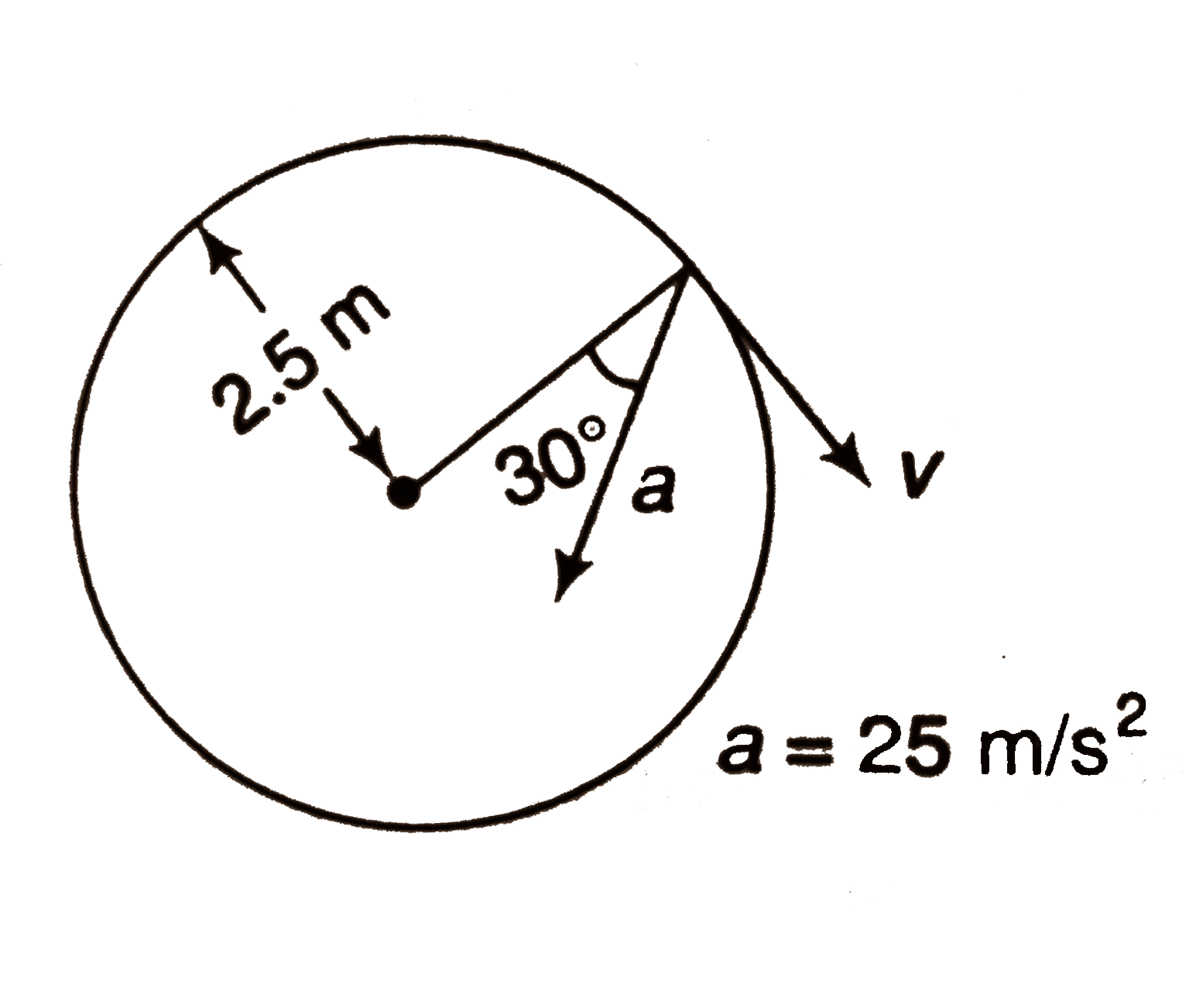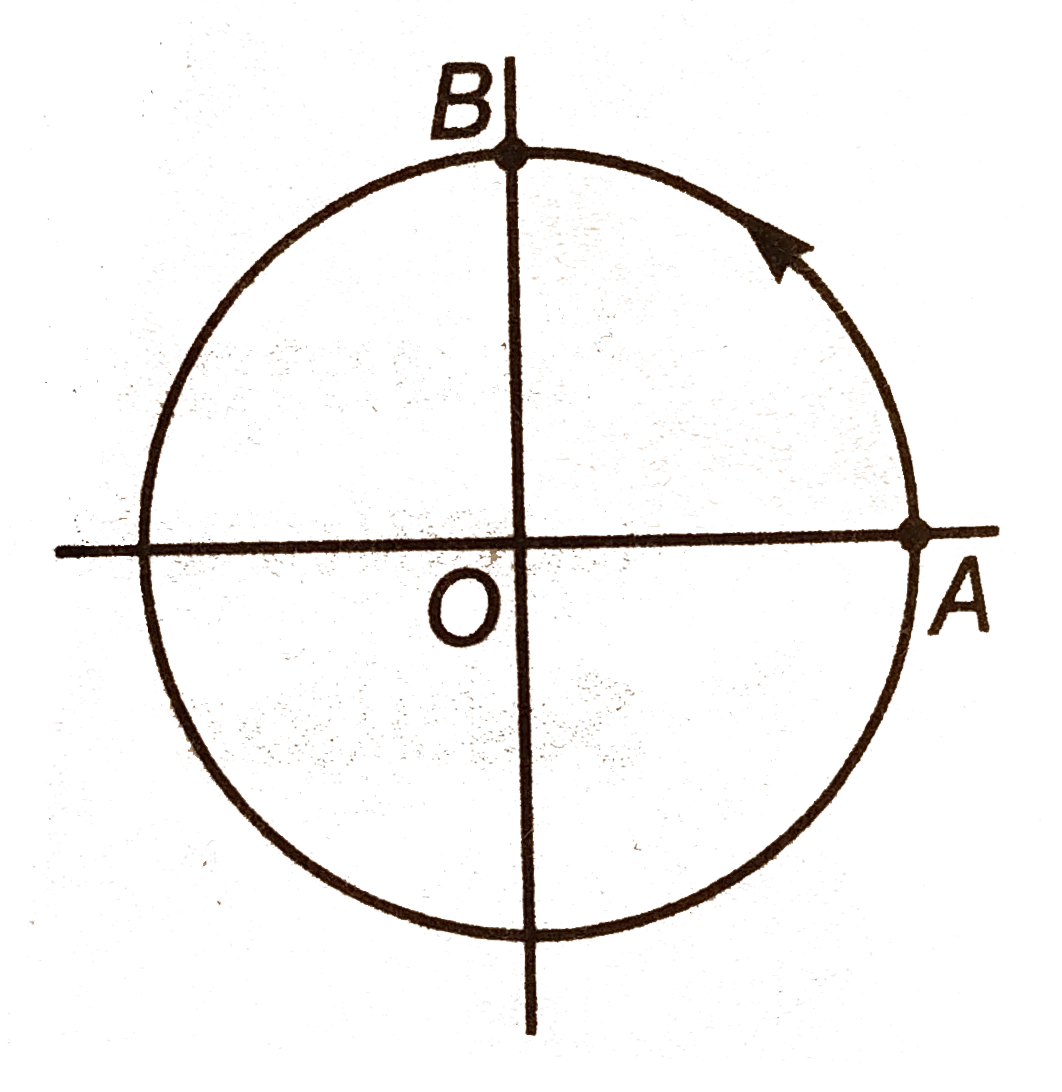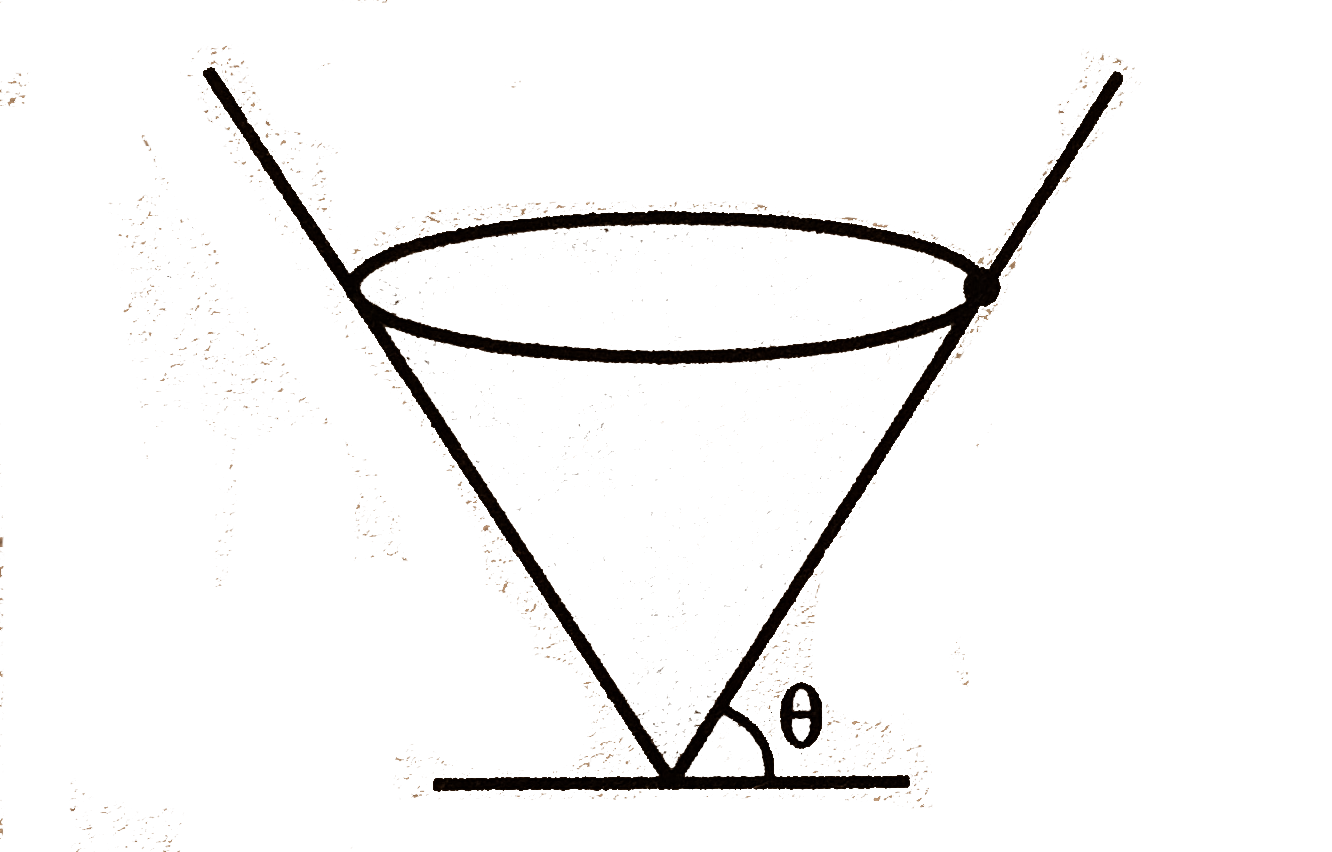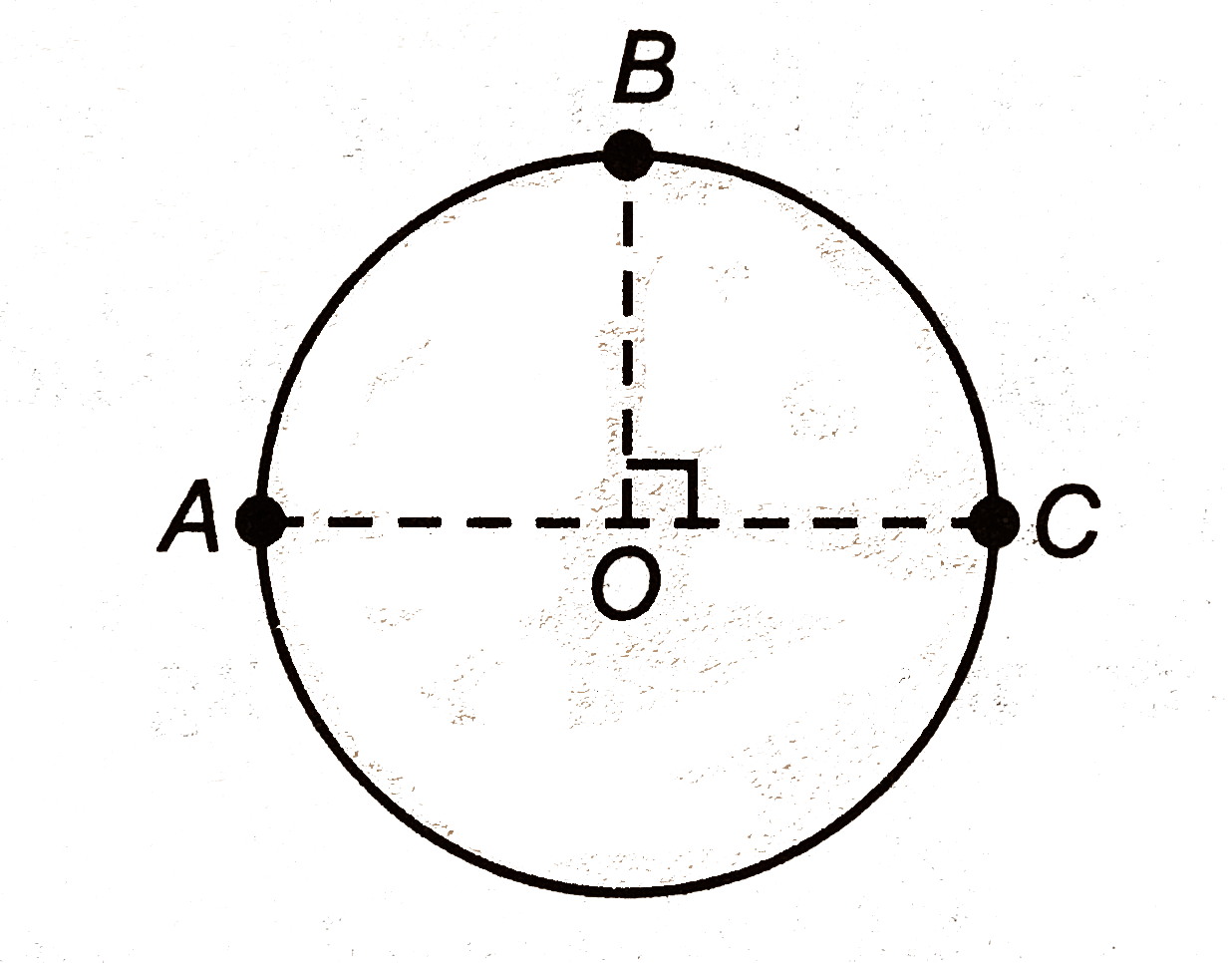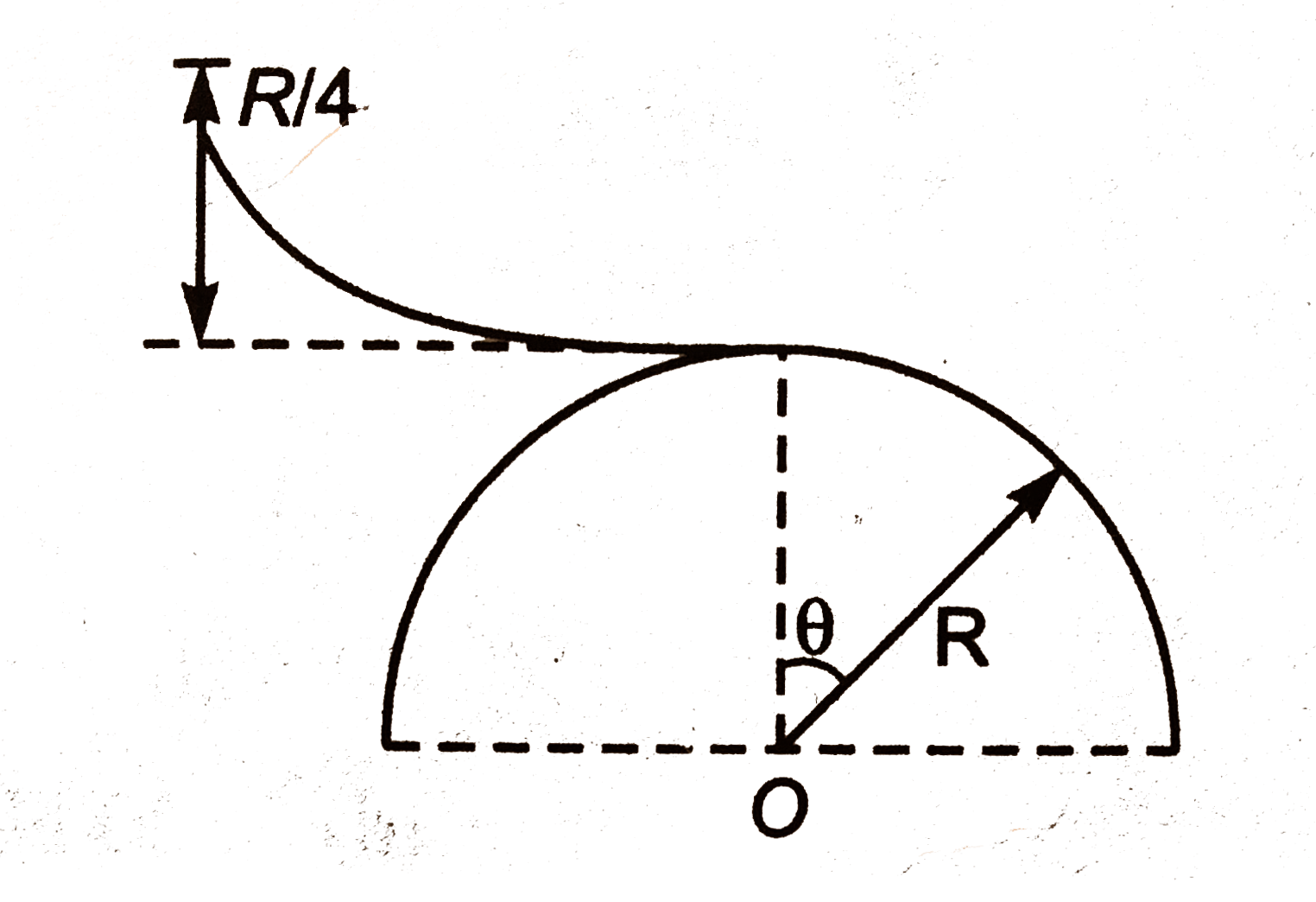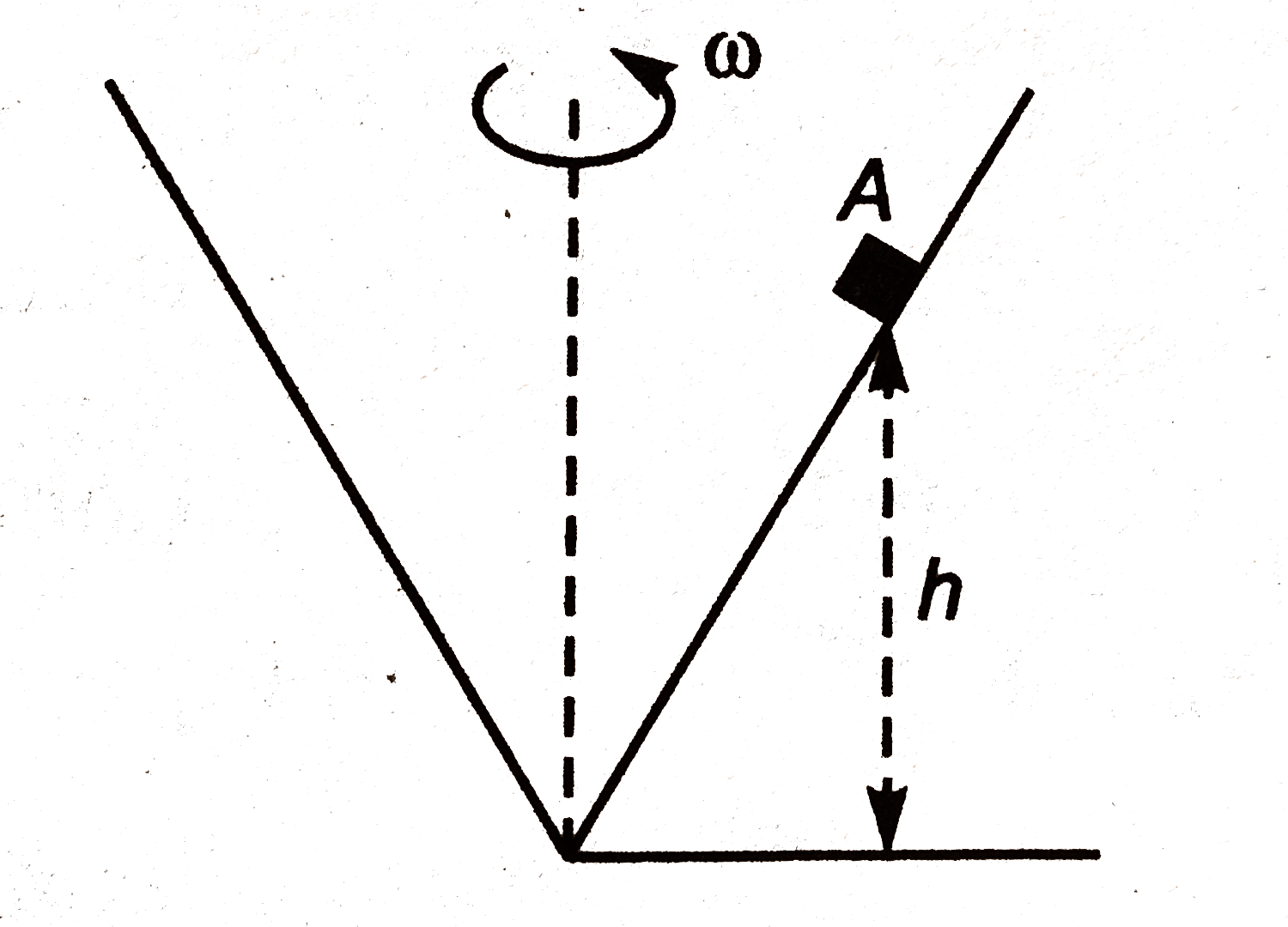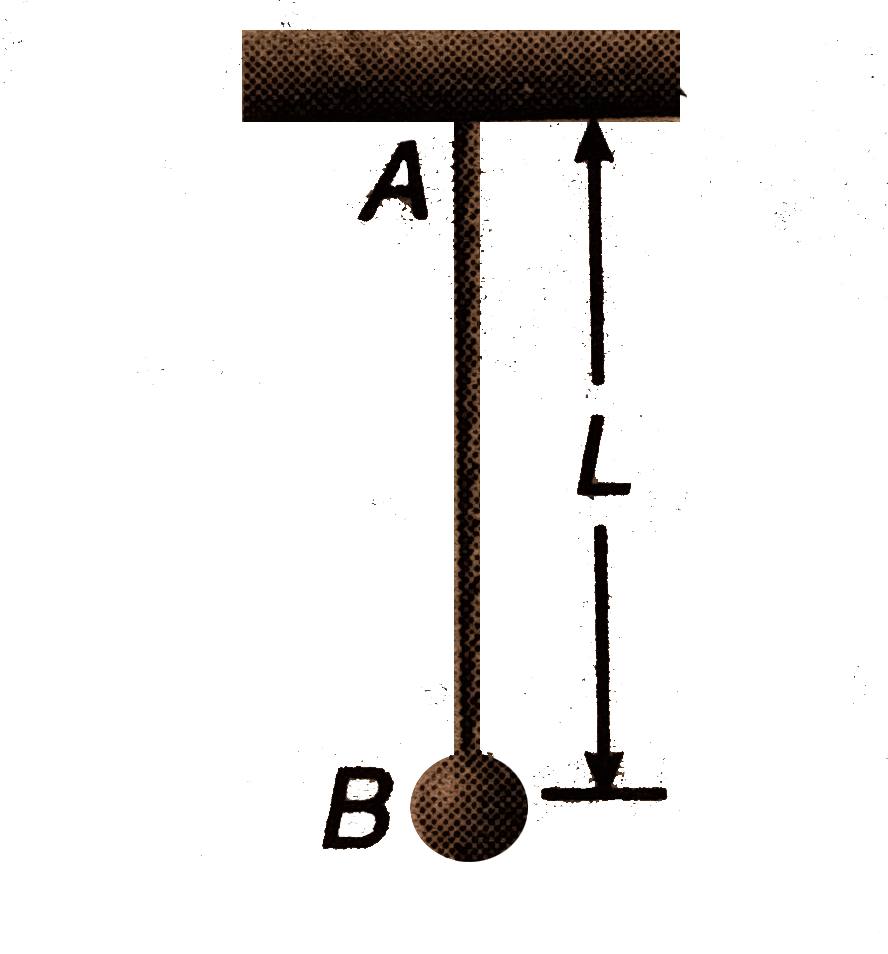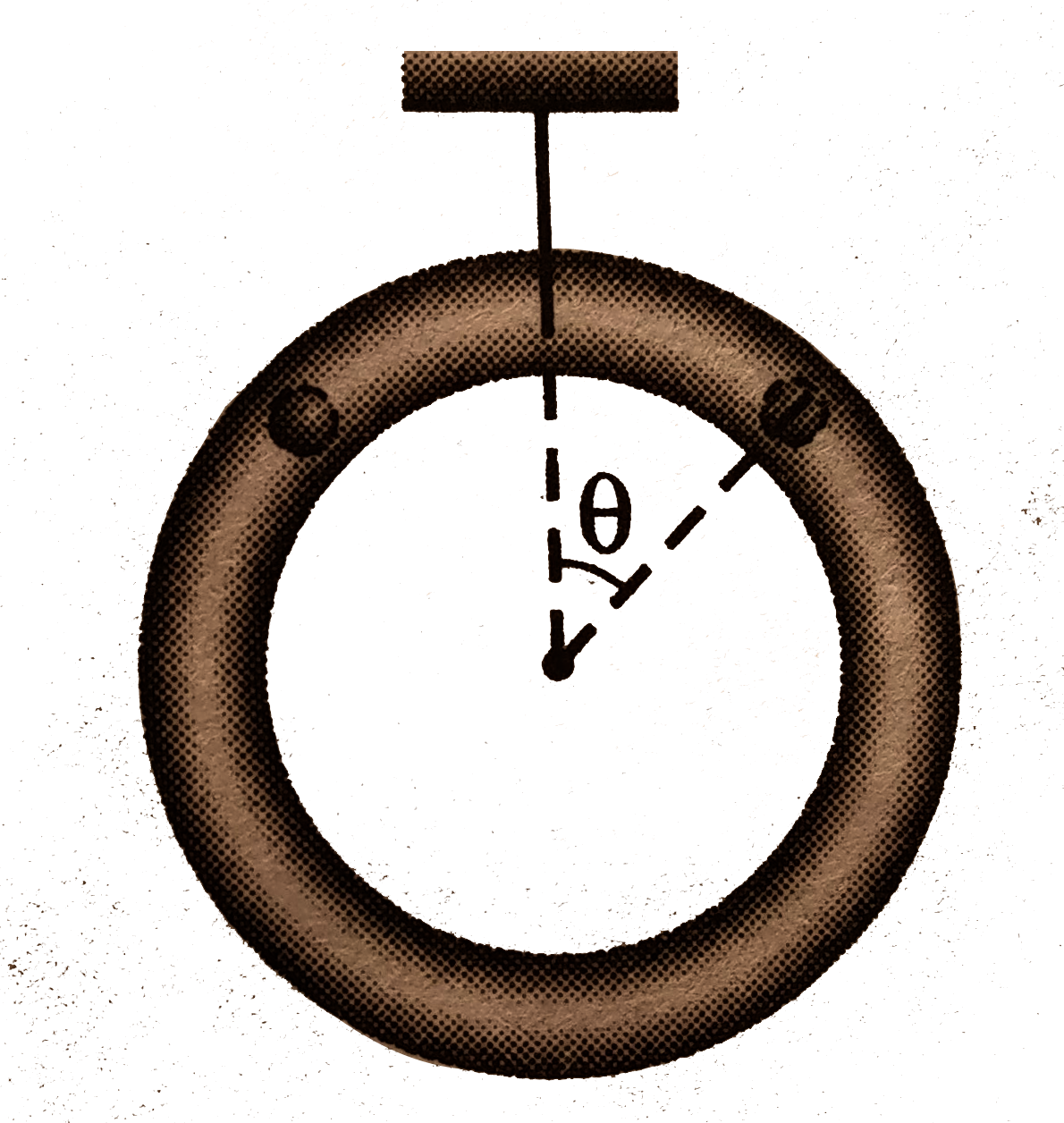Exercise 10.1 from DC PANDEY PHYSICS (HINGLISH) CIRCULAR MOTION for Class 11
| Class 11 | PHYSICS |
| Chapter | CIRCULAR MOTION |
| DC PANDEY PHYSICS (HINGLISH) | Exercise 10.1 |
| Medium | English |
| Academic Year | 2023-2024 |
Question 3
A particle moves in a circle of radius 1.0cm with a speed given by v=2t , where v is in cm/s and t in seconds.
(a) Find the radial accerleration of the particle at t=1s .
(b) Find the tangential accerleration of the particle at t=1s .
Find the magnitude of net accerleration of the particle at t=1s .View SolutionQuestion 13
A 4kg block is attached to a vertical rod by means of two strings of equal length. When the system rotates about the axis of the rod, the strings are extended as shown in figure.
(a) How many revolutions per minute must the system make in order for the tension in the upper string to be 200N ?
(b) What is the tension in the lower string then ?
 View Solution
View SolutionQuestion 14
A car moves at a constant speed on a straigh but hilly road. One section has a crest and dip of the 250m radius.
(a) As the car passes over the crest the normal force on the car is half the 16kN weight of the car. What will the noraml force on the car its passes through th ebottom of the dip?
(b) What is the greatest speed at which the car can move without leaving the road at the top of the hill ?
(c) Moving at a speed found in part (b) what will be the normal force on the car as it moves through the bottom of the dip? (Take, g=10m/s2) View SolutionQuestion 19
Assertion: A particle is irotating in a circle with constant speed as shown. Between point A and B , ratio of average acceleration and average velocity v can be stopped in a minimum distanc ed . If the same car, moving with same speed v takes a circular turn, then minimum safe radius can be 2d .
Reasion: d=v22μg and minimum safe radius =v2μg View SolutionQuestion 24
Assertion: In vertical circular motion, acceleration of bob at position A is greater than 'g'.<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/DCP_V01_C10_E01_006_Q01.pngwh=80%mx-autosty≤=background:white;><br>Reason:Netae≤rationatA is resultant of tangential and radial components of acceleration. View SolutionQuestion 41
A simple pendulum of length l and bob of mass m is displaced from its equilibrium position O to a position P so that height of P above O is h . If is then released. What is the tension in the string when the bob passes through the through the equilibrium position O ? Neglect friction. v is the velocity of the bob at OView SolutionQuestion 45
A 70kg man stands in contact against the inner wall of a hollw cylindrical drum of radius 3m rotating about its verticle axis. The coefficient of friction between the wall and his clothing nis 0.15 . What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed? View SolutionQuestion 46
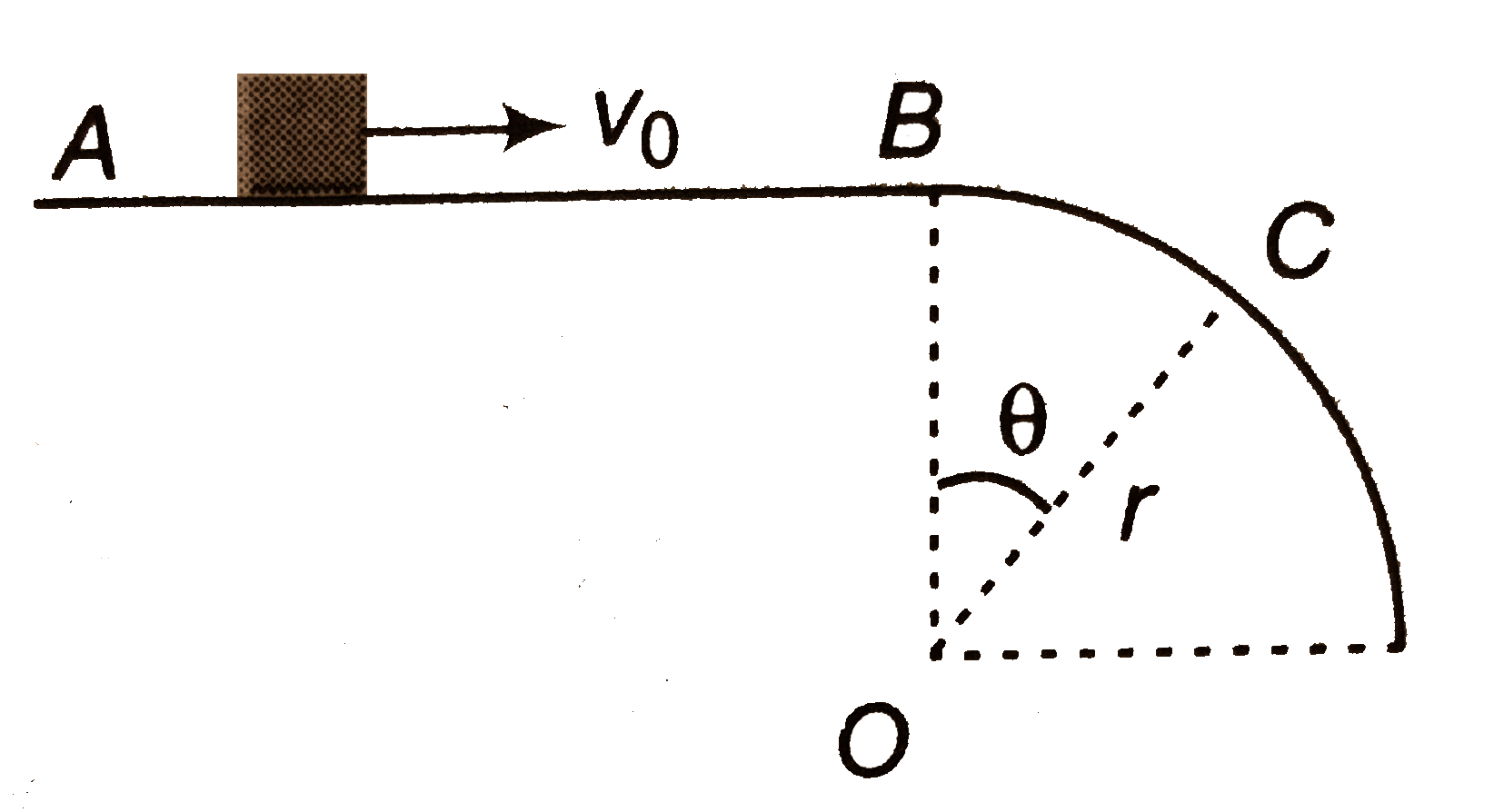
A particle is projected with a speed u at angle θ with the horizontal. Consider a small part of its path near the highest position and take it approximately to be a circular arc. What is the radius of this circle? This radius is called the adius of curvature of the curve at the point.View SolutionQuestion 48
A hemispherical bowl of radius R is set rotating about its axis of symmetry which is kept vertical. A small block kept in the bowl rotates with the bowl without slipping on its surface. If the surfaces of the bowl is smooth, and the angel made by the radius through the block with the vertical is θ, find the angular speed at which the bowl is rotating.View SolutionQuestion 50
A boy whirls a stone of small mass in a horizontal circle of radius 1.5m and at height 2.9m above level ground. The string breaks and the stone flies off horizontally and strikes the ground after travelling a horizontal distance of 10m . What is the magnitude of the centripetal acceleration of the stone while in circular motion ?View SolutionQuestion 51
A block of mass m is kept on a horizontal ruler. The frilction coefficient between the ruler and the block is μ. The ruler is fied at one end and the block is at a distance L from the fied end. The ruler is rotated about the fixed end in the horizontal plane through the fixed end. a. What can the maximum angular speed of the ruler isuniformly increased from zero t an angular acceleration α , at what angular speed will the block slip?View SolutionQuestion 52
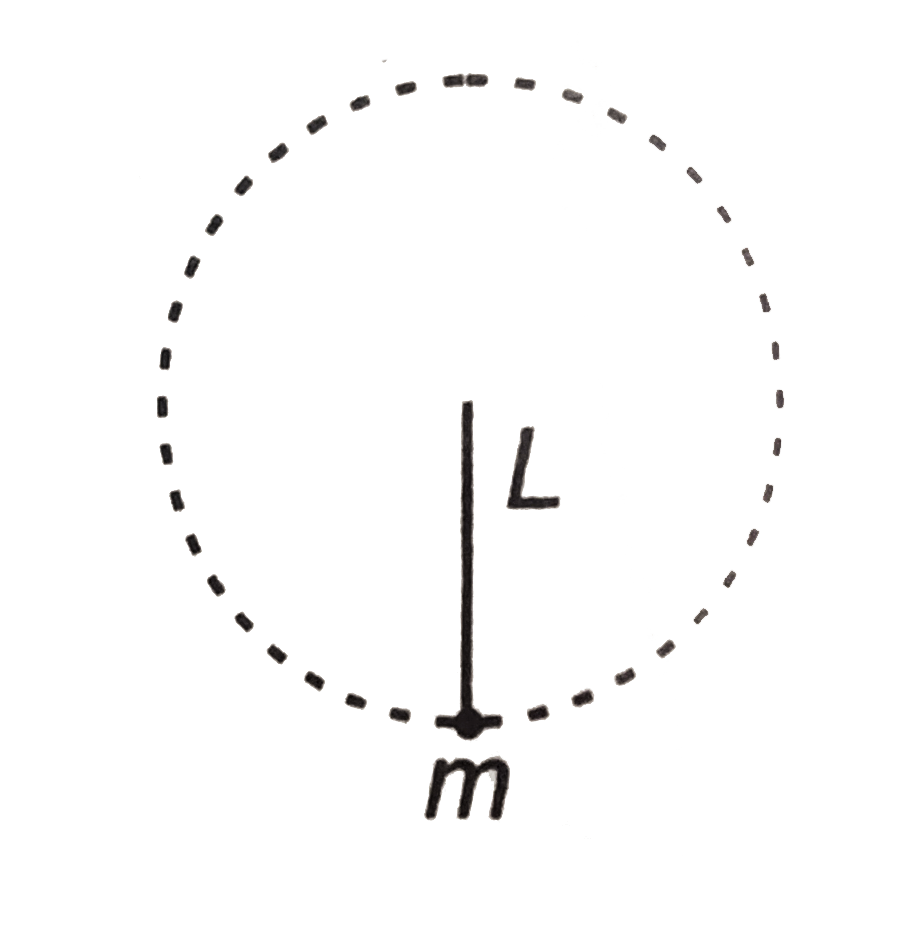
A thin circular wire of radius R rotatites about its vertical diameter with an angular frequency ω . Show that a small bead on the wire remain at its lowermost point for ω≤√g/R . What is angle made by the radius vector joining the centre to the bead with the vertical downward direction for ω=√2g/R ? Neglect friction. View SolutionQuestion 53
Two block tied with a massless string of length 3m are placed on a rotating table as shown. The axis of rotation is 1m from 1kg mass and 2m from 2kg mass. The angular speed
ω=4rad/s . Ground below 2kg block is smooth and below 1kg block is rough. (g=10m/s2)
(a) Find tension in the string, force of friction on 1kg block and its direction.
If coefficient of friction between 1kg block and groung is μ=0.8 Find maximum angular speed so that neither of the blocksd slips.
(c) If maximum tension in the string can be 100N , then maximum angular speed so that neither of the blocks slips.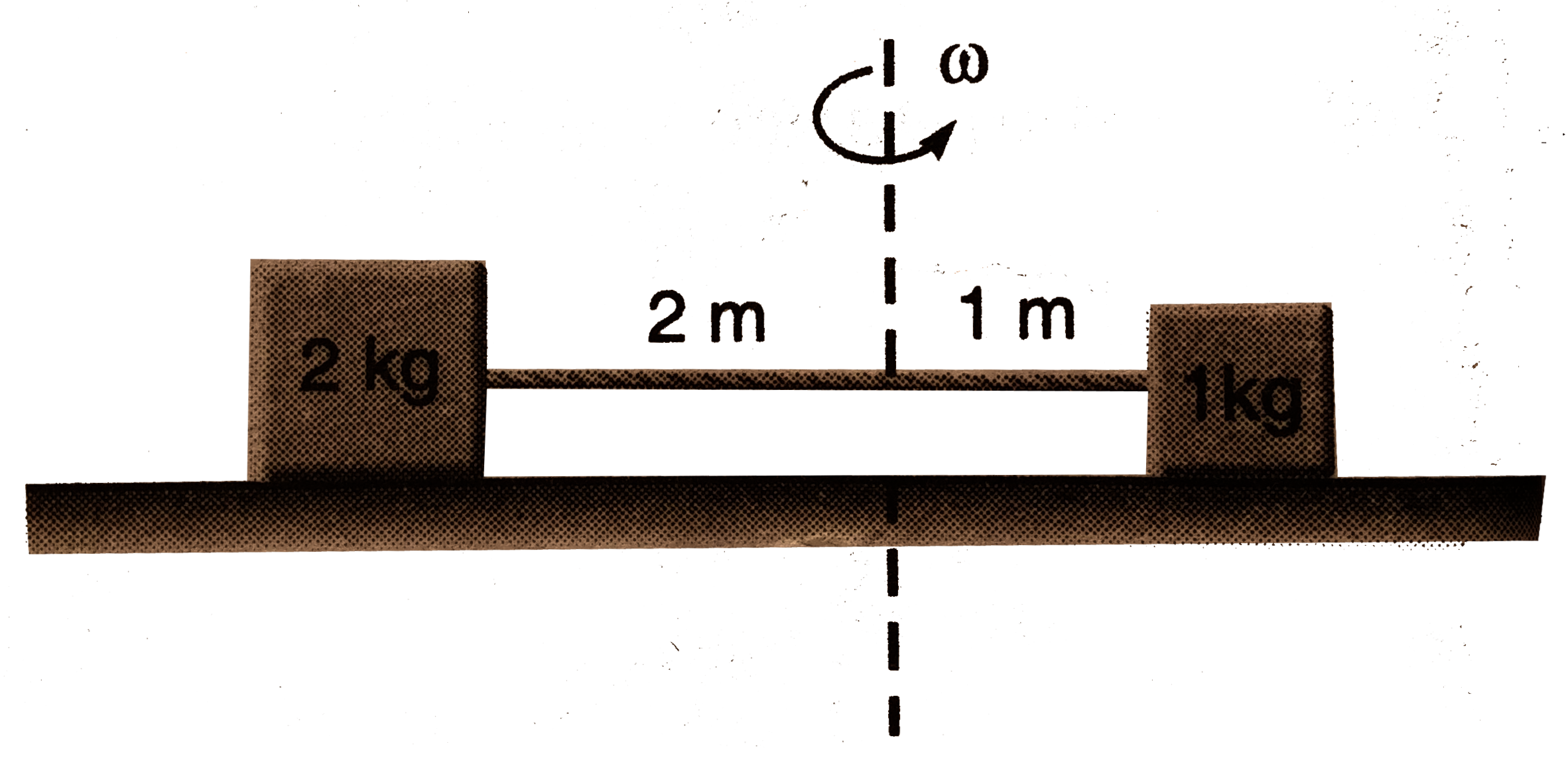 View Solution
View SolutionQuestion 56
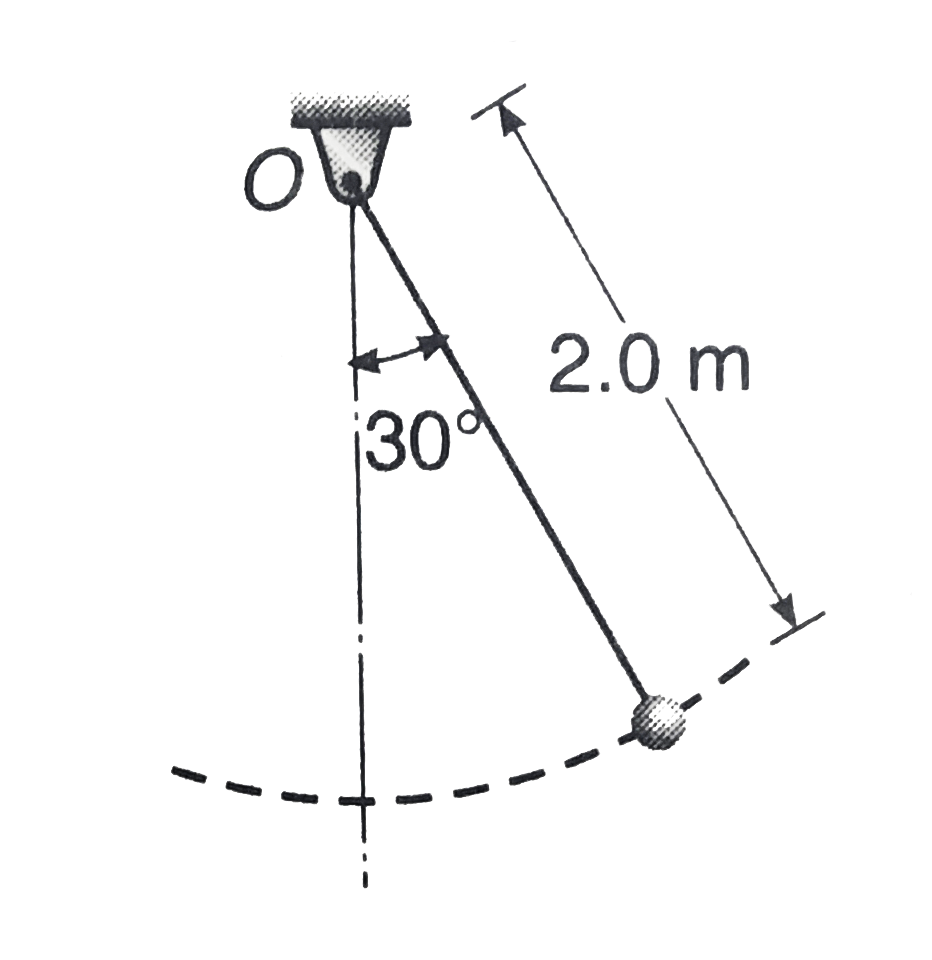
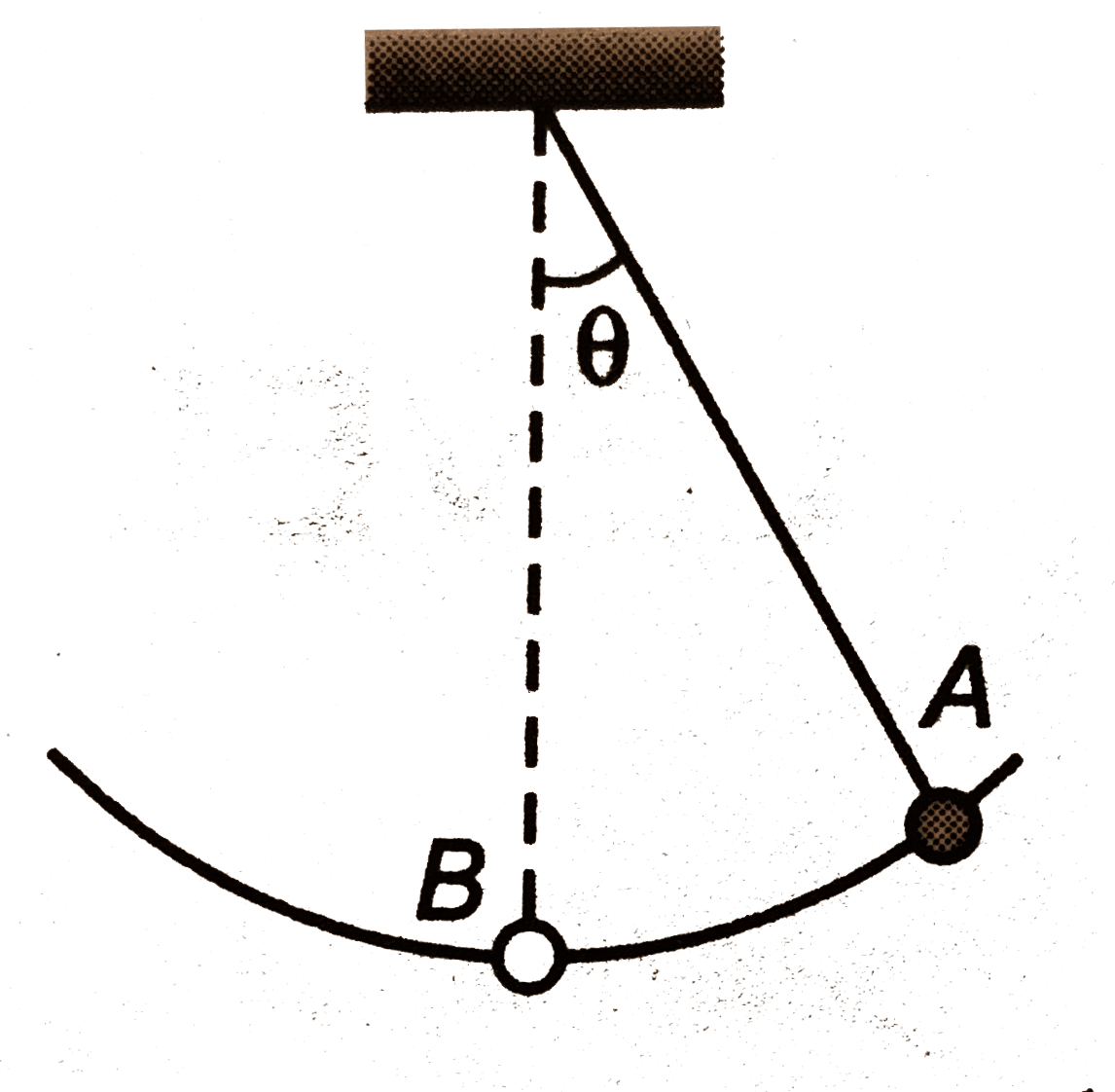
The sphere at A is given a downward velocity v0 of magnitude 5m/s and swings in a vertical plane at the end of a rope of length l=2m attached to a support at O . Determine the angle θ at which the rope will breack, knowing that it can withstant a maximum tension equal to twich the weight of the sphere.
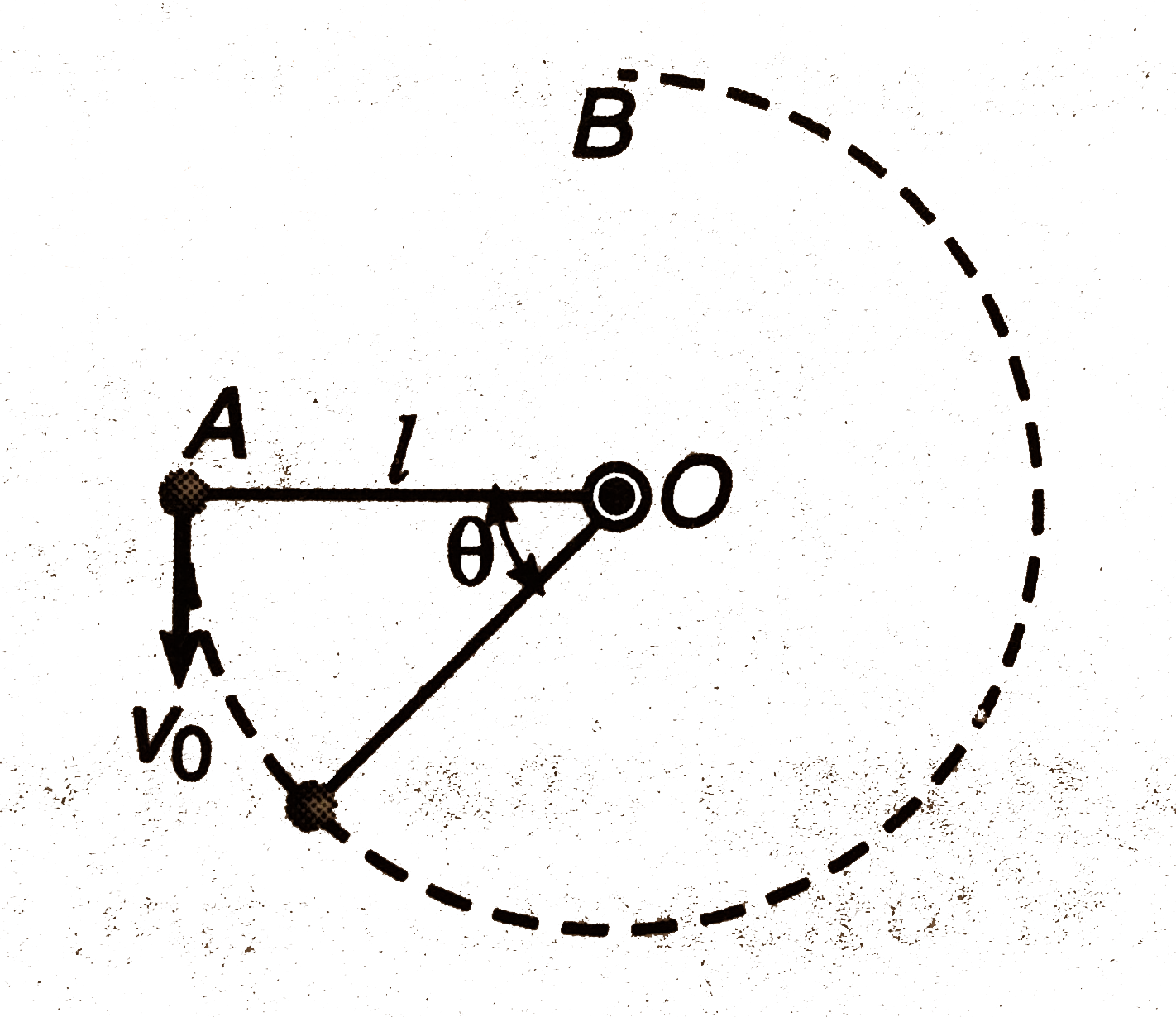 View Solution
View SolutionQuestion 59
A rough horizontal plate rotates with angular velocity ω about a fixed verticle axis. A particle or mass m lies on the plate at a distance 5a4 from this axis. The coefficient of friction between the plate and the particle is 13 . The largest value of ω2 for which the oparticle will continue to be at rest on the revolving plate is View SolutionQuestion 63
A particle is projected with velocity u horizontally from the top of a smooth sphere of radius a so that it slides down the outside of the spher. If the particle leaves the outsides down th eoutside of the sphere. If the particle leaves the sphere when it has fallen a height a4 , the value of u is View SolutionQuestion 66
A dics is rotating in a room. A boy standing near the rim of the disc of radius R finds the water droplet falling from the ceiling is always falling on his head. As one drop hits his head, other one starts from the ceiling. If height of the roof above his head is H , then angular velocity of the disc is View SolutionQuestion 73
A particle is moving in a circular path in the vertical plane. It is attached at one end of a string of length l whose other end is fixed. The velocity at lowest point is u. The tension in the string T and acceleration of the particle is a any position. Then T is zero at highest point ifView SolutionQuestion 76
A small spherical ball is suspended through a string of length l . The whole arrangement is placed in a vehicle which is moving with velocity v . Now, suddenly the vehicle stops and ball starts moving along a circular path. If tension in the string at the highest point is twice the weight of the ball then (assume that the ball completes the vertical circle) View SolutionQuestion 77
A particle is describing circular motion in a horizontal plane in contact with the smooth surface of a fixed rigid circular cone with its axis vertical and vertex down. The height of the plane of motion above the vertex is h and the semi-vertical angle of the cone is α The period of revolution of the particle
 View Solution
View SolutionQuestion 80
A ball with mass m is attached to the end of a rod of mass M and length l. The other end of the rod is pivoted so that the ball can move in a vertical circle. The rod is held in the horizontal position as shown in figure and then given just enough a downward push so that the ball swings down and just reaches the vertical upward position having zero speed there. Now answer the following questions.
The change in potential energy of the system (ball+rod) is
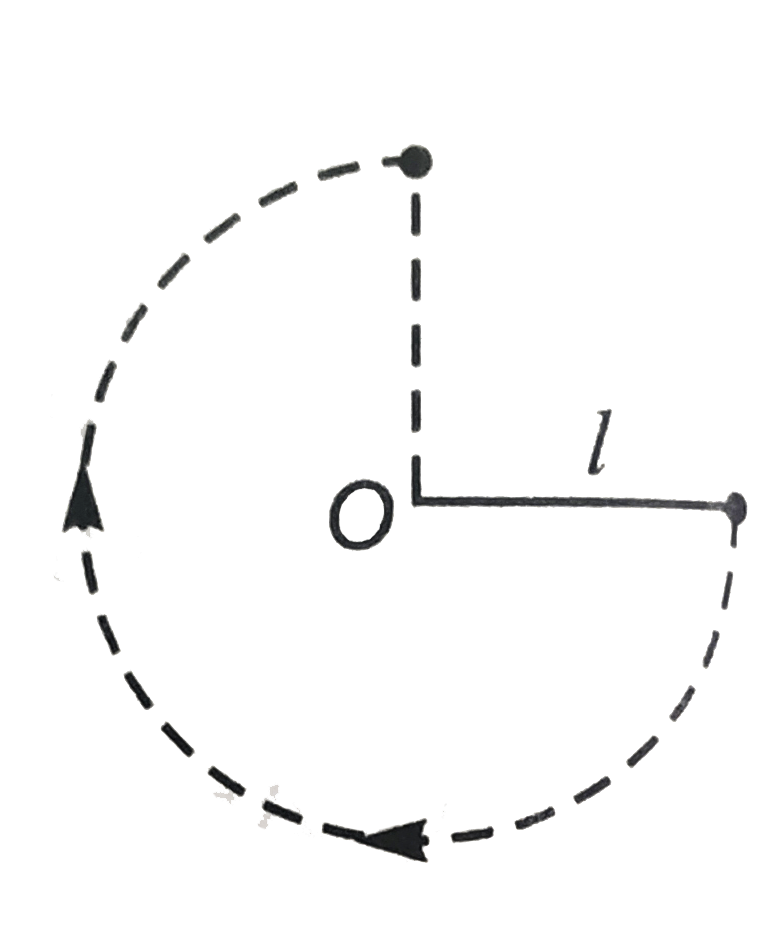 View Solution
View SolutionQuestion 81
A ball with mass m is attached to the end of a rod of mass M and length l. The other end of the rod is pivoted so that the ball can move in a vertical circle. The rod is held in the horizontal position as shown in figure and then given just enough a downward push so that the ball swings down and just reaches the vertical upward position having zero speed there. Now answer the following questions.
The initial speed given to the ball is
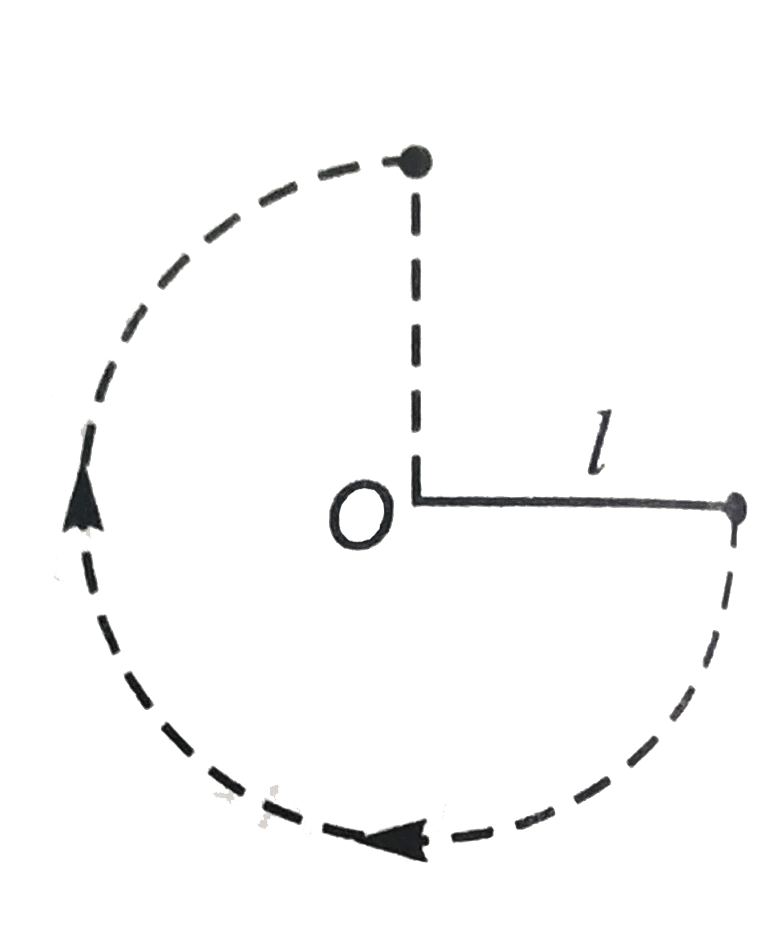 View Solution
View SolutionQuestion 83
A small particle of mass m attached with a light inextensible thread of length L is moving in a vertical circle. In the given case particle is moving in complete vertical circle and ratio of its maximum to minimum velocity is 2:1 .
Kinetic energy of the particle at the lower most position is
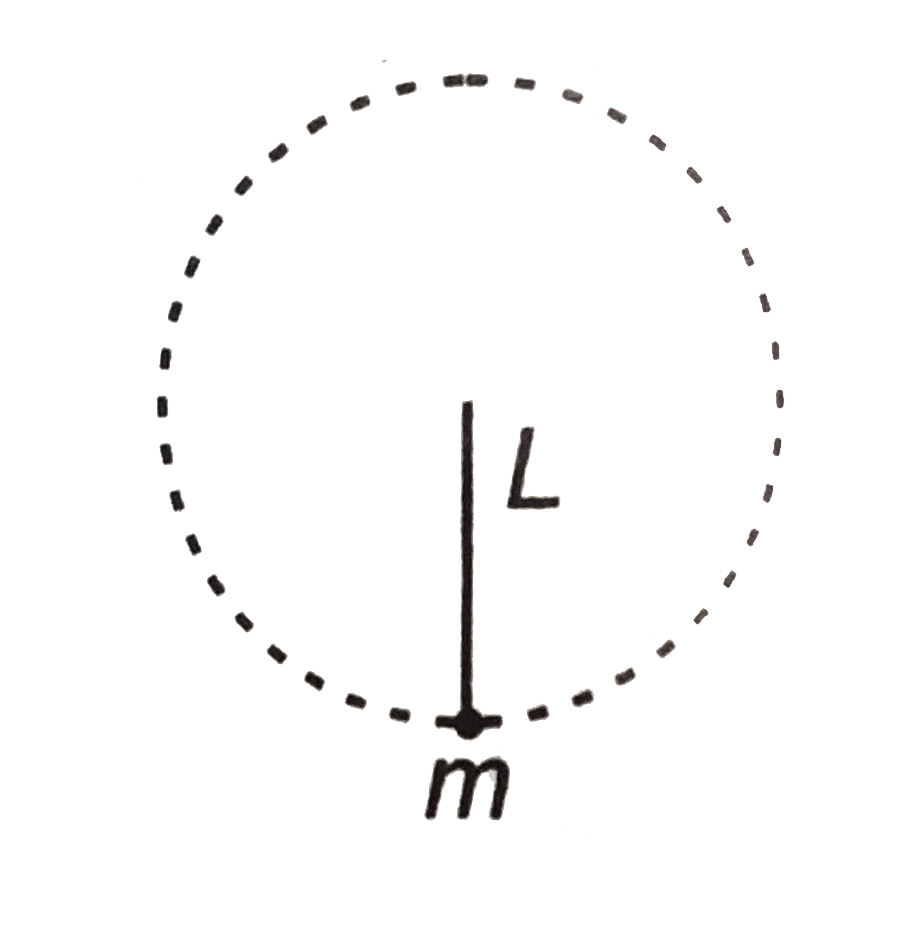 View Solution
View SolutionQuestion 84
A small particle of mass m attached with a light inextensible thread of length L is moving in a verical circle. In the given case particle is moving in complete vertical circle and ratio of its maximum to minimum velocity is 2:1 .
Velocity of the particle when it is moving certically downward is
 View Solution
View SolutionQuestion 86
A small sphere B of mass m is released form rest in the position shown and swings freely in a vertical plane, first about O and then about the peg A after the cord comes in contact with the peg. Determime the tension in the cord
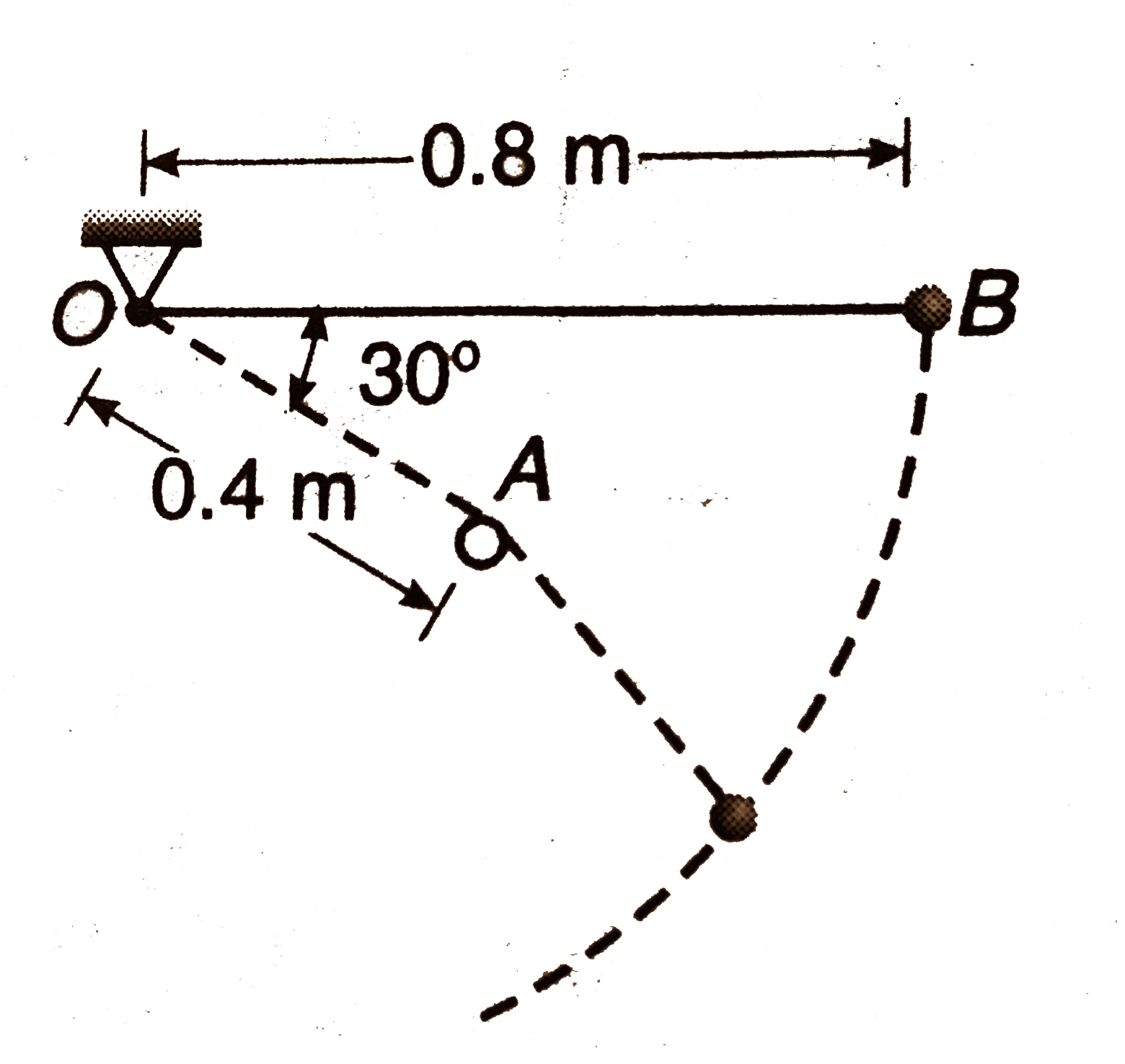
(a) just before the sphere comes in contact with the peg.
(b) just after it comes in contact with the peg. View SolutionQuestion 87
A particle of mass m is suspended by a string of length l from a fixed rigid support. A sufficient horizontal velocity =√3gl is imparted to it suddenly. Calculate the angle made by the string with the vertical when the accekleration of the particle is inclined to the string by 45∘ .View SolutionQuestion 91
If the system shown in the figure is rotated in a horizontal circle with angular velocity ω . Find (g=10m/s2)
(a) the minimum value of ω to start relative motion between the two blocks.
(b) tension in the string connecting m1 and m2 when slipping just starts between the blocks
The coefficient of frition between the two masses is 0.5 and there is no friction between m2 and ground. The dimensions of the masses can be neglected. (Take R=0.5m,m1=2Kg,m2=1Kg)
 View Solution
View SolutionQuestion 92
The simple 2Kg pendulum is released from rest in the horizontal position. As it reaches the bottom position, the cord wraps around the smooth fixed pin aat B and continues in the smaller arc in the vertical plane. Calculate the magnitude of the force R supported by the pin at B when the pendulum passes the position θ=30∘,(g=9.8m/s2)
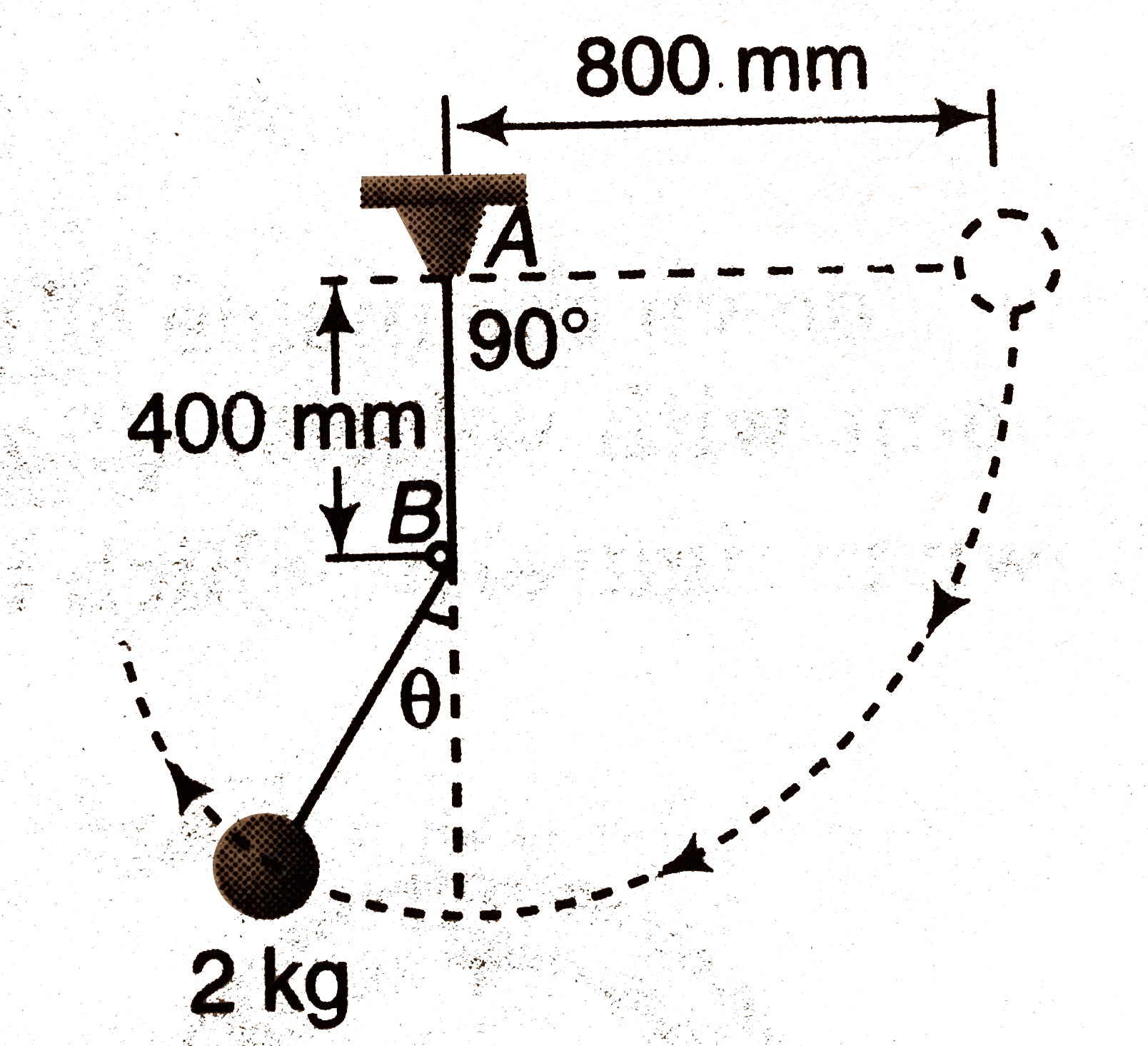 View Solution
View SolutionQuestion 93
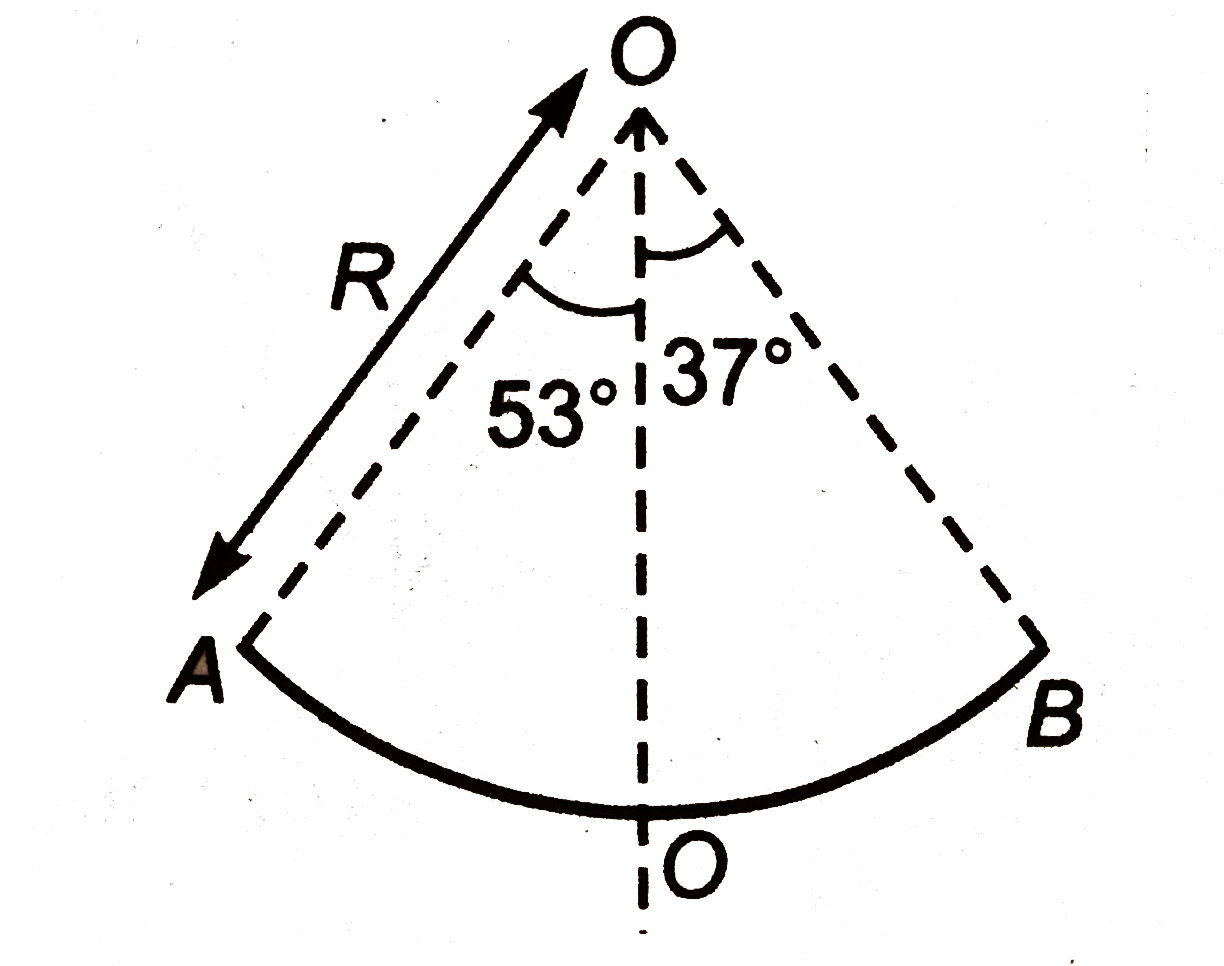
A circular tube of mass M placed veticlly on a horizontal surface as shown in the figure. Two small spheres, each of mass m , just fit in the tube, are released from the top. If θ gives the angle between radius vector of eirther ball with the vertical, obtain the value of the ratio M/m if the tube breacks its contact with ground when θ=60∘ . Neglect any friction.
 View Solution
View SolutionQuestion 94
A table with smooth horizontal surface is turning at an angular speed ω about its axis. A groove is made on the surface along a radius and a particle is gently placed inside the groove at a distance a from the centre. Find the speed of the speed of the particle as its distance from teh centre becomes L.View SolutionQuestion 95
A block of mass m slides 0n a frictionless table. It is constrained to move inside a ring of radius R . At time t=0 , block is moving along the inside of the ring (i.e. in the tangential direction) with velocity v0 . The coefficient of friction between the block and the ring is μ . Find the speed of the block at time t .
 View Solution
View SolutionQuestion 97
A smooth circular tube of radius R is fixed in a vertical plane. A particle is projectid from its lowest point with a velocity just sufficient to carry it to th ehigest point. Show that the time taken by the particle to rach the end of the horizontal diameter is (√Rg)In(1+√2) .
Hint : ∫secθ.dthη=In(secθ+tanθ) View SolutionQuestion 98
A heavy partile slides under gravity download the inside of a smooth vertical tube dheld in vertical plane. It starts from the highest point with velocity √2ag , where a is the radius of the circle. Find the angular position θ (as shown in figure) at which the vertical acceleration of the particle is maximum.
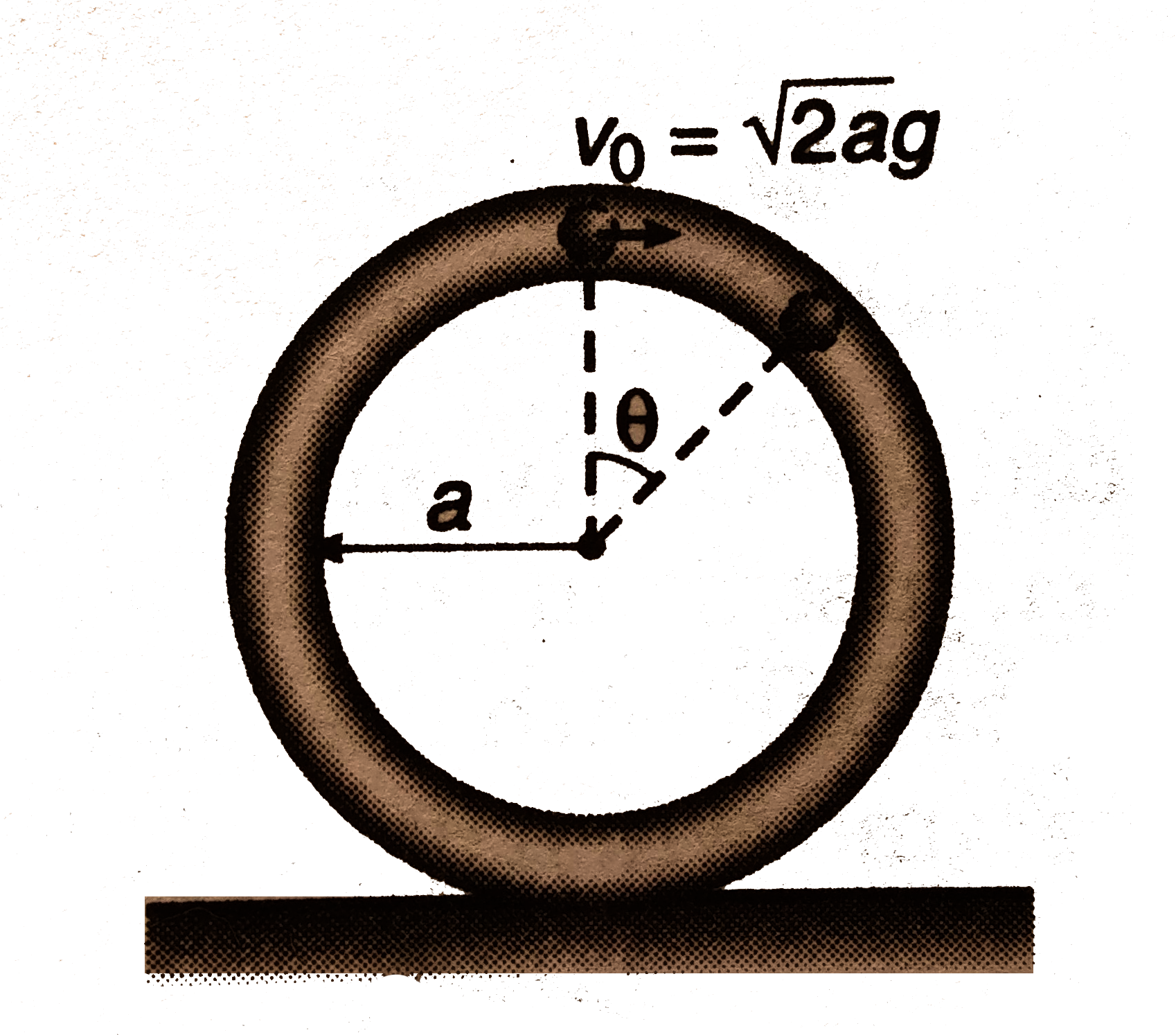 View Solution
View SolutionQuestion 99
A vertical frictionless semicircular track of radius 1m fixed on the edge og a movable trolley (figure). Initially, the system is rest and a mass m is kept at the top of the track. The trolly starts moving to the right with a uniform horizontal acceleration a=2g/9 . The mass slides down the track, eventually losing contact with it and dropping to the floor 1.3m below the trolly. This 1.3m is from the point where mass loses contact. (g=10m/s2)
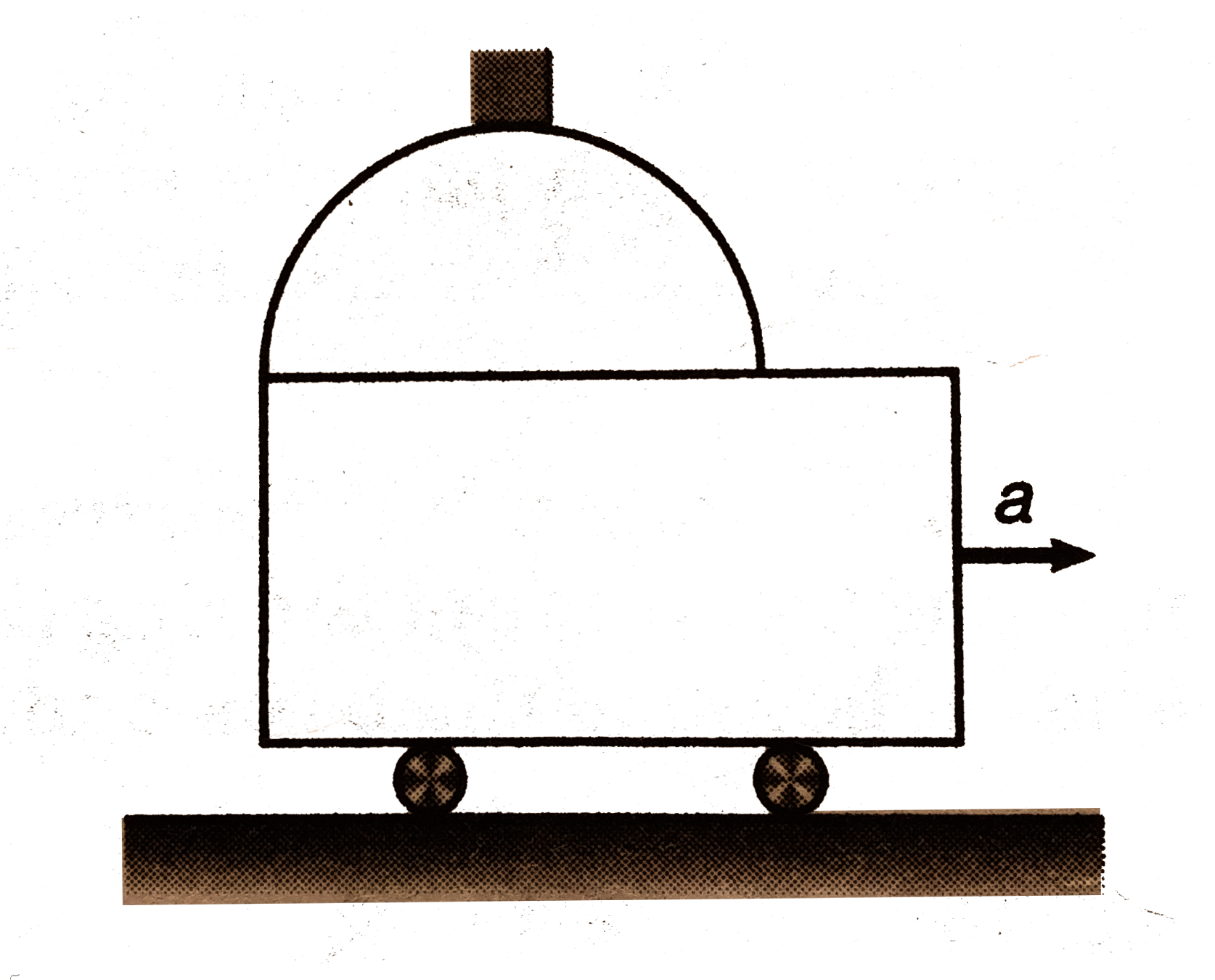
(a) Calculate the angle θ at which it loses contact with the trolly and
(b) the time taken by the mass to drop on the floor, after losing contact. View Solution
All Exercises from DC PANDEY PHYSICS (HINGLISH) Class 11 PHYSICS CIRCULAR MOTION
- ASSERTION AND REASON
- CHECK POINT
- COMPREHENSION
- EXERCISE 10.1
- EXERCISE 10.2
- EXERCISE 10.3
- INTEGER
- JEE ADVANCED
- JEE MAIN
- LEVEL 1 OBJECTIVE
- LEVEL 1 SUBJECTIVE
- LEVEL 2 COMPREHENSION BASED
- LEVEL 2 MORE THAN ONE CORRECT
- LEVEL 2 SINGLE CORRECT
- LEVEL 2 SUBJECTIVE
- MATCH THE COLUMNS
- MATRIX MATCHING
- MEDICAL ENTRANCES S GALLERY
- MORE THAN ONE OPTION IS CORRECT
- SUBJECTIVE QUESTIONS
- TAKING IT TOGETHER
- EXAMPLE
- MISCELLANEOUS EXAMPLES
- SOLVED EXAMPLES