SOLVED EXAMPLES TYPE H from PRADEEP PHYSICS (HINGLISH) GRAVIATION for Class 11
| Class 11 | PHYSICS |
| Chapter | GRAVIATION |
| PRADEEP PHYSICS (HINGLISH) | SOLVED EXAMPLES TYPE H |
| Medium | English |
| Academic Year | 2023-2024 |
Question 23
The mass of planet Jupiter is 1.9×1027kg and that of the Sun is 1.99×1030kg. The mean distance of Jupiter from the Sun is 7.8×1011m. Calculate the gravitational force which Sun exerts on Jupiter. Assuming that Jupiter moves in circular orbit around the Sun, also calculate the speed of Jupiter G=6.67×10−11Nm2kg−2.View SolutionQuestion 27
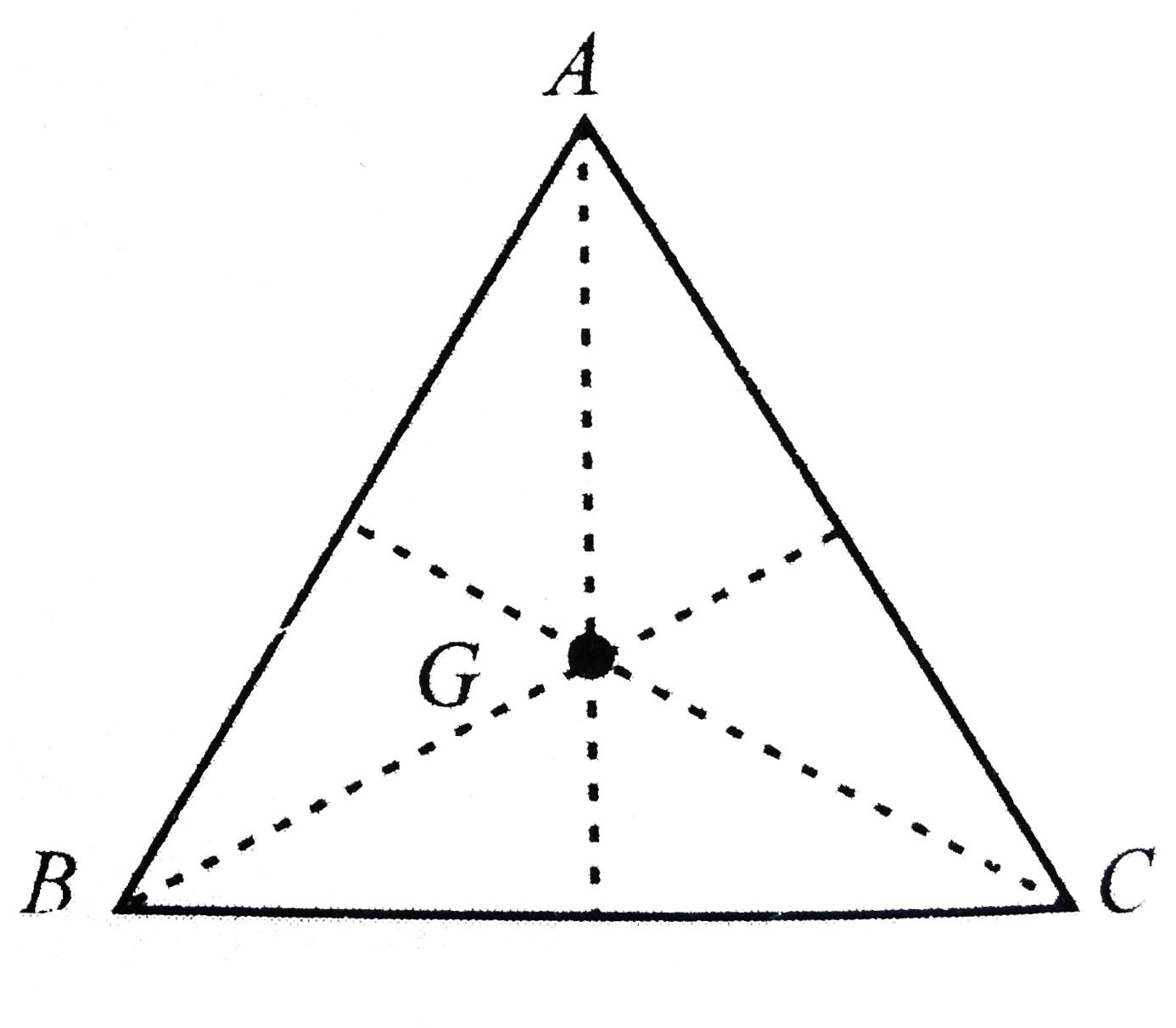
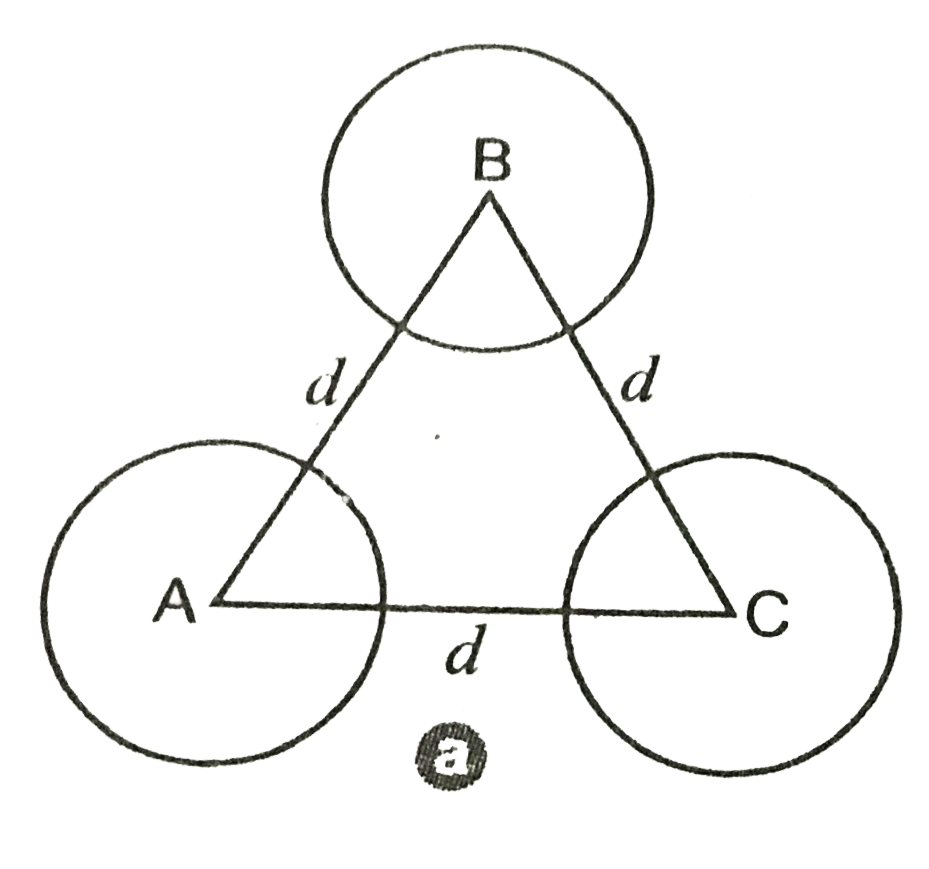
Three identical particles each of mass "m" are arranged at the corners of an equiliteral triangle of side "L". If they are to be in equilibrium, the speed with which they must revolve under the influence of one another's gravity in a circular orbit circumscribing the triangle is View SolutionQuestion 34
Two lead spheres of 20cm and 2cm diametre respectively are planet with centres 100cm apart. Calculate the attraction between them, given the radius of the Earth as 6.37×108cm and its mean density as 5.53×103kgm−3. Speciffic gravity of lead =11.5. If the lead spheres are replaced by bress sphere of the same radii, would the force of attraction be the same?View SolutionQuestion 54
A point mass body of mass 2kg is placed at a distance 20cm from one end of a uniform rod of length 2m and mass 10kg. Calculate
(i) gravitational intensity at the location of point mass body due to the rod.
(ii) gravitational force on the body due to the rod. Use G=6.67×10−11Nm2kg−2.View SolutionQuestion 65
In a two stage launch of a satellite, the first stage bringe the satlilte to a height of 500km and the second stage given it the necessary critical speed to put it in circular orbit around the Earth. Which stage requires more expenditude of fuel?
(Neglect damping due to air resistance, especially in the first stage).
Mass of the Earth =6.0×1024kg,radius of Earth =6400km,G=6.67×10−11Nm2kg−2.View SolutionQuestion 69
A block hole is a body from whose surface nothing may even escape. What is the condition for a uniform spherical body of mass M to be a block hole? What should be the radius of such a black hole if its mass is nine times the mass of the earth?
Mass of earth =6×1024kg,
G=6.61×10−11Nm2kg−2.View SolutionQuestion 73
Two uniform soild spheres of equal radii R but mass M and 4M have a centre to centre separation 6R, as shows in Fig. (a) The two spheres are held fixed. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the centre of ten second. Obtain an expression for the minimum speed υ of the projectile so that it reaches the surface of second sphere.
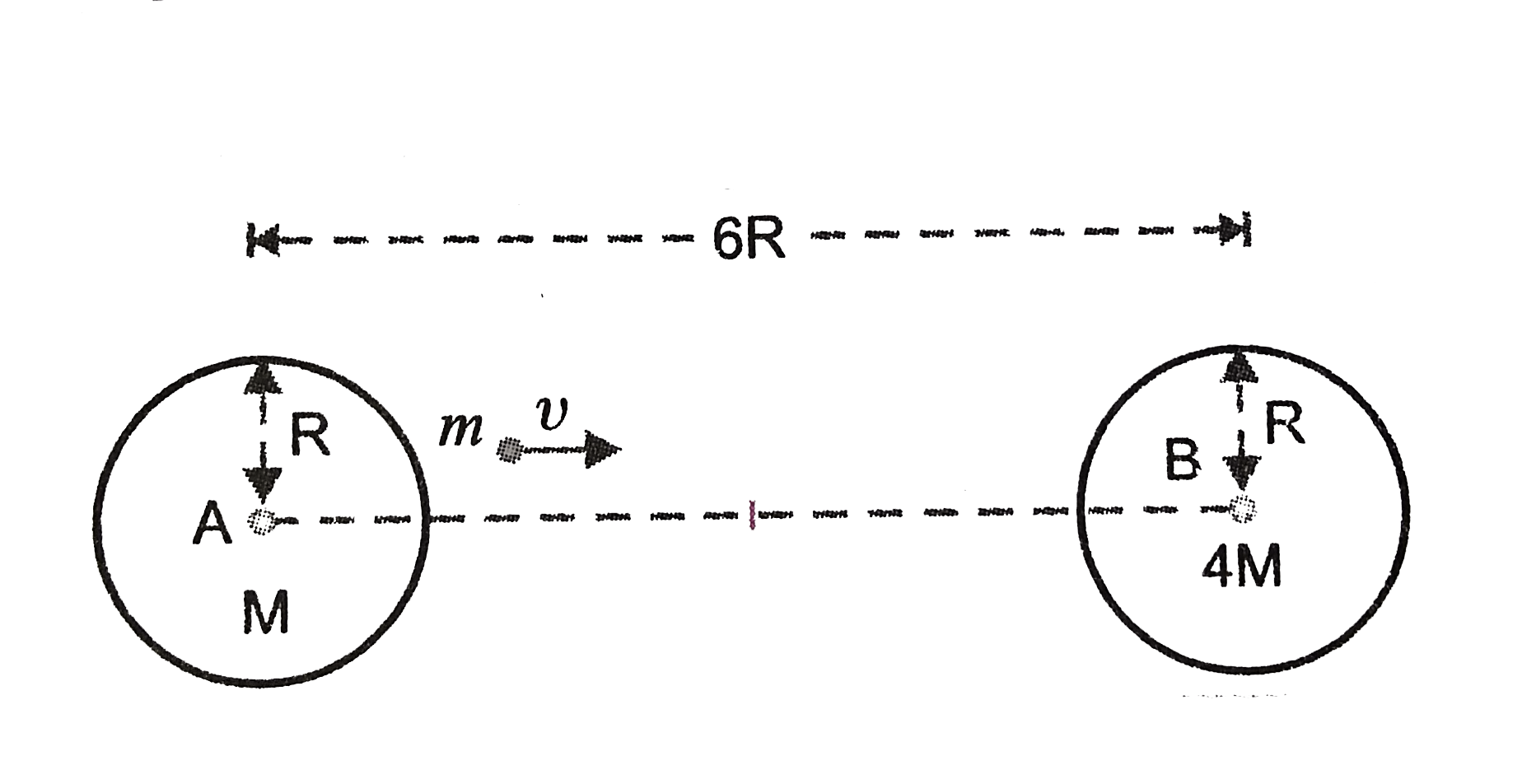 View Solution
View SolutionQuestion 74
The planet Mars has two moons. Phobos and Delmos (i) phobos has period 7 hours, 39 minutes and an orbital radius of 9.4×103km. Calculate the mass of Mars. (ii) Assume that Earth and mars move in a circular orbit around the sun, with the martian orbit being 1.52 times the orbital radius of the Earth. What is the length of the martian year in days? (G=6.67×10−11Nm2kg−2)View SolutionQuestion 77
Imagine a light planet revolving around a very massive star in a circular orbit of radius R with a period of revolution T. if the gravitational force of attraction between the planet and the star is proportational to R−5/2, then
(a) T2 is proportional to R2
(b) T2 is proportional to R7/2
(c) T2 is proportional to R3/3
(d) T2 is proportional to R3.75.View SolutionQuestion 106
A rocket of mass m is field vertically from the surface of Mars of mass M, radius R with a sped υ. If 20% of its initial energy is lost due to Martain atmosheric resistance, how far will the rocket go from the surface of Mars before returing to it? Let G be the gravational constant.View SolutionQuestion 123
Which of the following observations point to the equivalence of inertial and gravitational mass
(a) Two spheres of difference masses dropped from the top of a long evacuated reach the bottom of the tube at the same time.
(b) The time-period of a simple pendulum is independent on its mass.
(c) The gravitational force on a particle inside a hollow under isolated is zero.
(d)For a mass in a closed cabin that is falling freely under gravity, gravity 'disappears'.
(e) An astronomer inside a spaceship orbiting around the Earth fells weightless.
(f) Planets orbiting around the sun obey kepler's third law (approximately).
(g) The gravitational force on a body due to the Earth is equal and opposite to the gravitational force on the Earth due to the body.View SolutionQuestion 153
Choose the correct alternative :
(a) If the gravitational potential energy of two mass points infinite distance away is taken to be zero, the gravitational potential energy of a galaxy is (positive /negative/zero).
(b) The universe on the large is shaped by (gravitational/electromagentic) forces, on the atomic scale by (gravitational/electromagnetic) forces, on the nuclear scale by (gravitational/electromagnetic/strongnuclear) forces.View SolutionQuestion 211
An artificial satellite is moving in a circular orbit around the earth with a speed equal to half the magnitude of escape velocity from the earth.
(i) Determine the height of the satellite above the earth's surface.
(ii) If the satellite is stopped suddenly in its orbit and allowed to fall freely onto the earth, find the speed with which it hits the surface of the earth.View SolutionQuestion 231
There are three identical point mass bodies each of mass m locted at the vertices of an equilateral triangle with side r. They are exerting gravitational force of attraction on each other, which can be given by Newton's law of gravitaiton. Each mass body produces its gravitational field in the surrounding region. the magnitude of gravitational field at a point due to a point mass body is the measure of gravitaitonal intensity at that point. The gravitational potential at a point in a gravitational field is the amount of workdone in bringing a unit mass body infinity to the given point without acceleration.
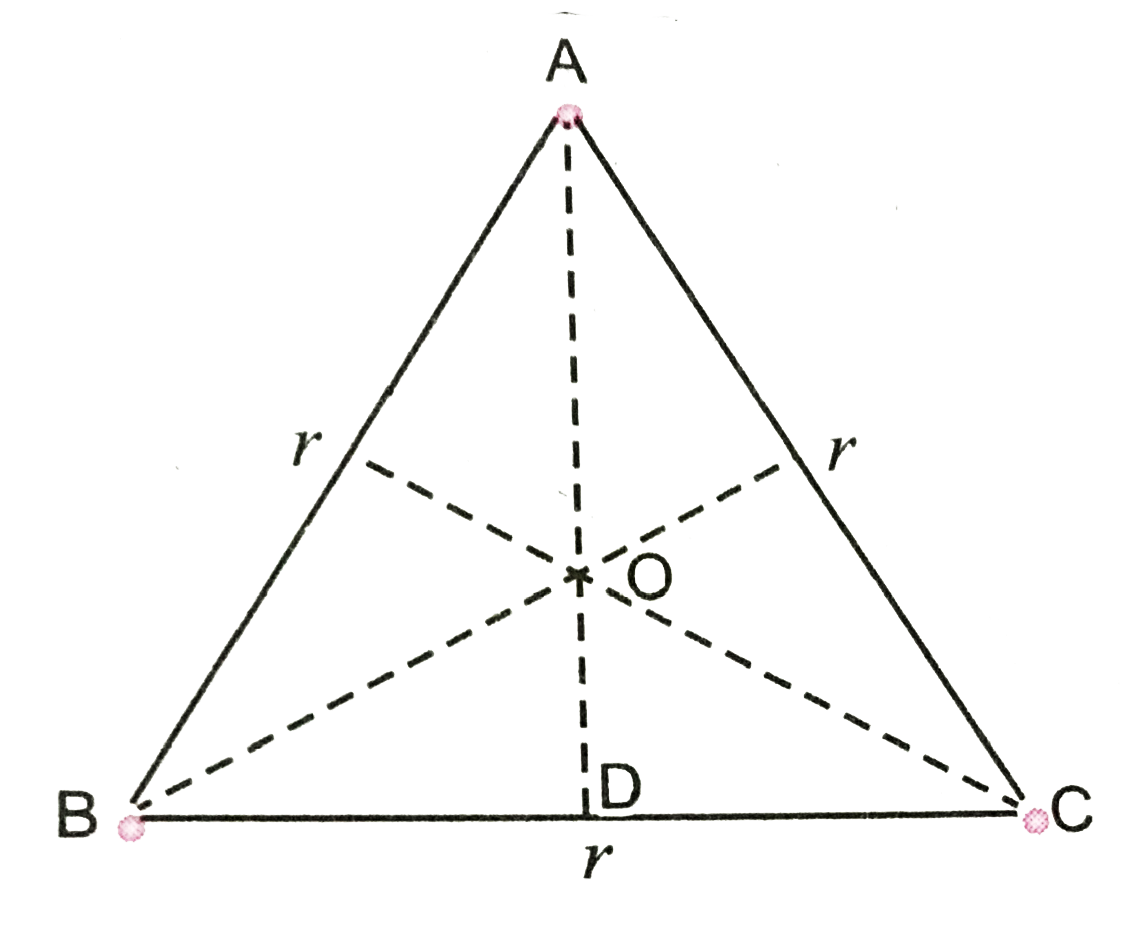
Answer the following questions :
At what speed must they move if they all revolve under the influence of one another's gravitation in a circular orbit circumsribing the triangle still preserving the equilateral triangleView SolutionQuestion 236
An artificial satellite is moving in a circular orbit around the earth with a speed equal to half the magnitude of escape velocity from the earth.
(i) Determine the height of the satellite above the earth's surface.
(ii) If the satellite is stopped suddenly in its orbit and allowed to fall freely onto the earth, find the speed with which it hits the surface of the earth.View SolutionQuestion 240
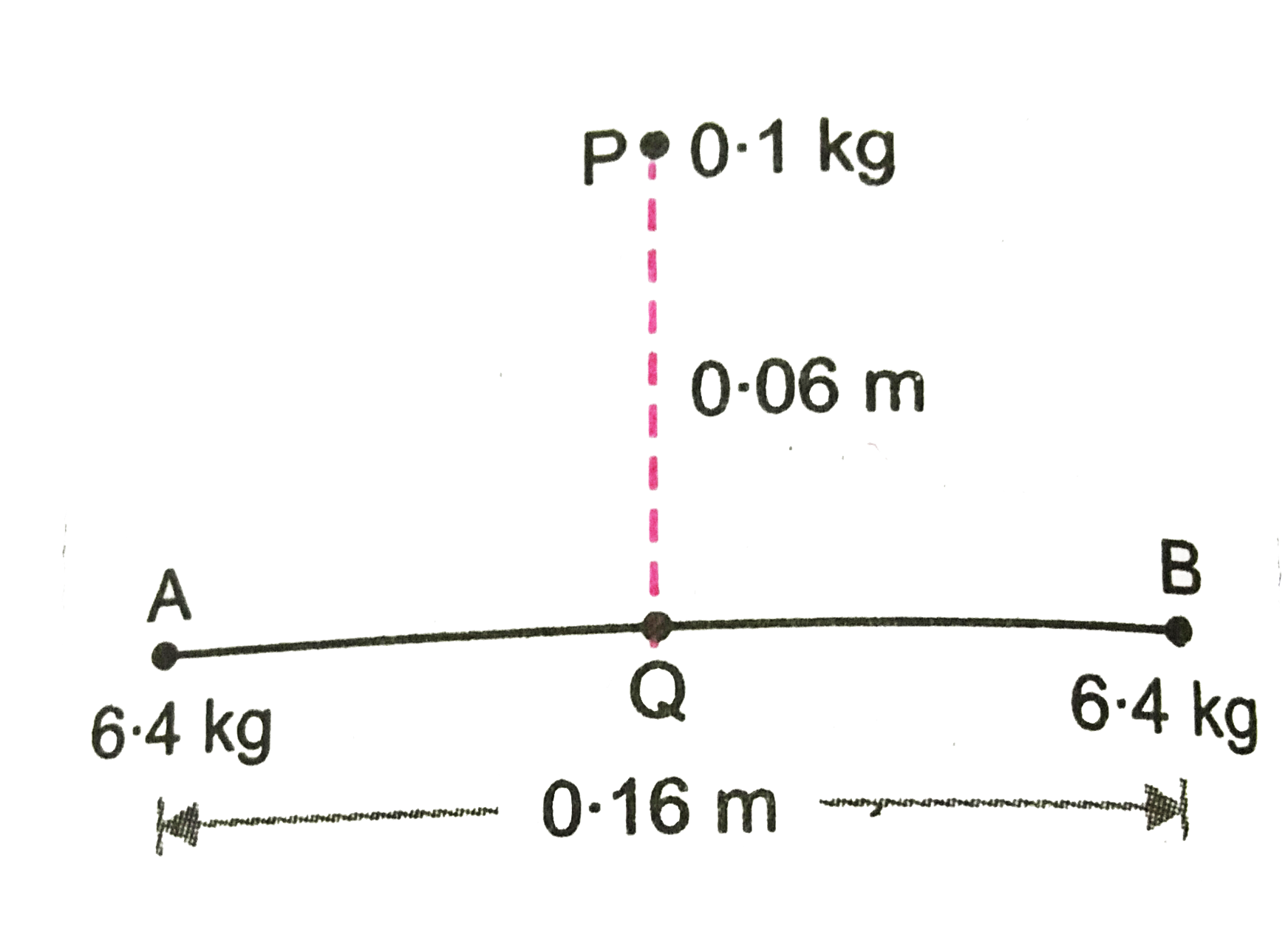
Two equal masses of 6.40kg are separted by a distance of 0.16m. A small body is released from a point P, equidistant from the two masses and at a distance of 0.06m from the line joining them. Fig.
(a) Calculate the velocity of this body when it passes through Q.
(b) Calculate the acceleration of this body at P and Q if its mass is 0.1kg.
Use G=6.67×10−11Nm2kg−2
 View Solution
View SolutionQuestion 241
Distance between the centres of two stars is 10α. The masses of these stars are M and 16M and their radii a and 2a, respectively. A body of mass m is fired straight form the surface of the larger star towards the smaller star. What should be its minimum inital speed to reach the surface of the smaller star? Obtain the expression in terms of G,M and a.View SolutionQuestion 243
A satellite of mass 10kg is placed initially in a temporary orbit 800km above the surface of earth. The satellite is to be placed now in a permanent orbit at 2000km above the surface of earth. Find the amount of workdone to move the satellite from temporary to permanent orbit. The radius of the earth is 6400km and g=10ms−2.View SolutionQuestion 246
Answer the following: (a) You can shield a charge from electrical forces by putting it inside a hollow conductor. Can you shield a body from the gravitational influence of nearby matter by putting it inside a hollow sphere or by some other means? (b) An astronaut inside a small spaceship orbiting around the Earth cannot detect gravity. If the space station orbiting around the Earth has a large size, can he hope to detect gravity? (c) If you compare the gravitational force on the Earth due to the Sun to that due to the Moon, you would find that the Sun’s pull is greater than the Moon’s pull. (You can check this yourself using the data available in the succeeding exercises). However, the tidal effect of the Moon’s pull is greater than the tidal effect of Sun. Why?View SolutionQuestion 247
Choose the correct alternative
(a)Acceleration due to gravity increase/decrease with increasing altitude.
(b) Acceleration due to gravity increase/decrease with increasing depth (assume the earth to be a sphere of uniform density).
(c ) Acceleration due to gravity is independer of mass of the earth/mass of the body.
(d) The formula −GMm(1r2−1r1) is more/less accurate than the formula mg(r2−r1) for the difference of potential energy between two points r2 and r1 distance away from the centre of earth.View SolutionQuestion 250
Let us consider that our galaxy consists of 2.5×1011 stars each of one solar mass. How long will this star at a distance of 50,000 light year from the galastic entre take to complete one revolution? Take the diameter of the Milky way to be 105ly.G=6.67×10−11Nm2Kg−2.(1ly=9.46×1015m)View SolutionQuestion 251
Choose the correct alternative :
(a) If the zero of the potential energy is at infinity, the total energy of an orbiting satellite is negative of its kinetic/potential energy.
(b) The energy required to rocket an orbiting satellite out of Earth's gravitational influence is more/less than the energy required to project a sationary object at the same height (as the satellite) out of Earth's influence.View SolutionQuestion 253
A comet orbits the Sun in a highly elliptical orbit. Does the comet have a constant (a) linear speed (b) angular speed (c) angular momentum (d) kinetic energy (e) potential energy (f) total energy throughout its orbit? Neglect any mass loss of the comet when it comes very close to the Sun.View SolutionQuestion 262
A rocket is fired vertically upwards with a speed of υ(=5kms−1) from the surface of earth. It goes up to a height h before returning to earth. At height h a body is thrown from the rocket with speed υ0 in such away so that the body becomes a satellite of earth. Let the mass of the earth, M=6×1024kg, mean radius of the earth, R=6.4×106m,G=6.67×10−11Nm2kg−2,g=9.8ms−2.
Answer the following questions:
The value of h is View SolutionQuestion 266
Two heavy sphere each of mass 100kg and radius 0.10m are placed 1.0m apart on a horizontal table. What is the gravitational field and potential at the mid point of the line joining the centres of the sphere? Is an object placed at that point in equilibrium? If so, is the equilbrium stable or unstable.View SolutionQuestion 267
A geostationary satellite orbits the Earth at a height of nearly 36,000km from the surface of earth. What is the potential due to earth's gravity at the site of tthis satllite ? (Take the potential energy at infinity to be zero). Mass of the Earth =6.0×1024kg, radius =6400km,G=6.67×10−11Nm2/kg2.View SolutionQuestion 268
A star 2.5 times the mass of the sun and collapsed to a size of the 12km rotates with a speed of 1.5 rev.per second. (Extremely compact stars of this kind are known as neutron stars. Centain onserved steller objects called pulsars are believed to belong this category ). Will an object placed on its equator remain struck to its surface due to gravity ? (Mass of the sun =2×1030kg).View SolutionQuestion 269
A space-ship is stationed on Mars. How much energy must be expended on the spaceship to rocket it out of the solar system ? Mass of the spaceship =1000kg, Mass of the sun =2×1030kg. Mass of the Mars =6.4×1023kg, Radius of Mars =3395km. Radius of the orbit Mars =2.28×1011m,G=6.67×10−11Nm2kg−2. View SolutionQuestion 270
A rocket of mass m is field vertically from the surface of Mars of mass M, radius R with a sped υ. If 20% of its initial energy is lost due to Martain atmosheric resistance, how far will the rocket go from the surface of Mars before returing to it? Let G be the gravational constant.View SolutionQuestion 288
A star like the sun has serveral bodies moving around it at different distance. Consider that all of them are moving in circular orbits. Let r be the distance of the body from the centre of the star and let its linear velocity be υ, angular velocity ω, kinetic energy K, gravitational potential energy U, total energy E and angular momentum L. As the radius r of the orbit increase, determine which of the above quantities increase and which ones decrease.View SolutionQuestion 290
A satellite is to be placed in equatorial geostationary orbit around earth for communication.
(a) Calculate height of such a satellite.
(b) Find out the minimum number of satellites that are needed to cover entire earth so that at least one satellites is visible from any point on the equator.
[M=6×1024kg,R=6400km,T=24h,G=6.67×10−11SIunits]View SolutionQuestion 291
Earth's orbit is an ellipse with ecentricity 0.0167. Thus earth's distance from the sun and speed as it moves around the sun varies from day to day. This means that the length of the solar day is not constant through the year. Assume that earth's spin axis is normal to its orbital plane and find out the lenght of the shortest and the longest day. A day should be taken from noon. Does this explain variation of lenght of the day during the year?View SolutionQuestion 292
A satellite is in an elliptical orbit around the earth with aphelion of 6R and perihelion of 2R where R=6400km is the radius of the earth. Find accentricity of the orbit. Find the velocity of the satellite at apogee and perigee. What should be done if this satellite has to be transferred to a circular orbit of radius 6R? [G=6.67×10−11SI units and M=6×1024kg]View SolutionQuestion 295
A missile is fired radially from the surface of earth (radius 6.4×106m) at a satellite, orbiting the earth. The satellite appears stationary vertically upwards from the point where the missile is launched. Its distance from the centre of the earth is 25.4×106m. Will the missile actually hit the satellite?View SolutionQuestion 296
At noon, the sun and the earth pull the objects on the earth's surface in opposite directions. At midnight, the sun and the earth pull these objects in same direction. Is the weight of an object as measured by a spring balance on the earth's surface , more at midnight as compared to its weight as noon?View SolutionQuestion 304
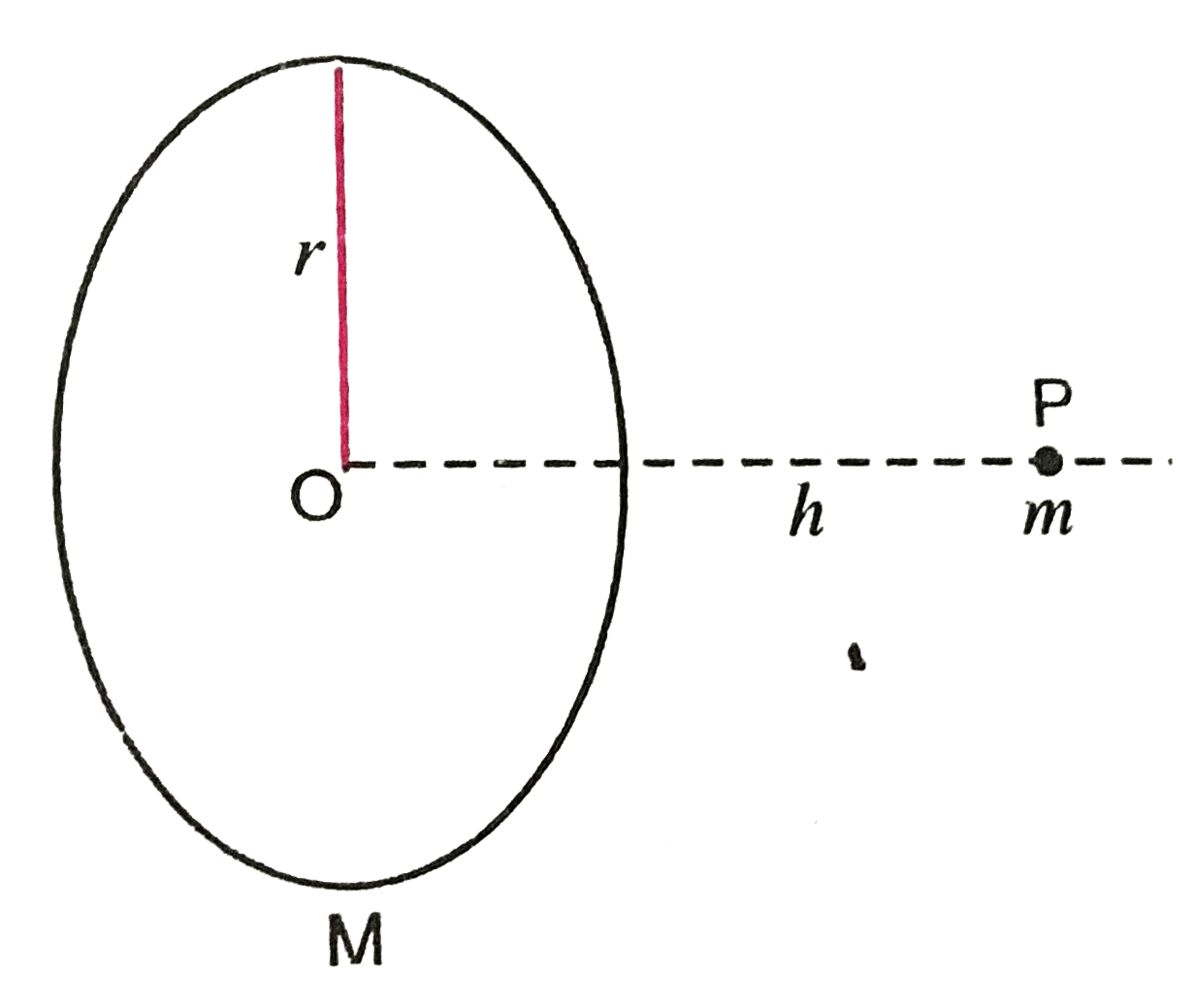
A solid sphere of uniform density and radius R applies a gravitational force of attraction equal to F1 on a particle placed at P, distance 2R from the centre O of the sphere. A spherical cavity of radius R/2 is now made in the sphere as shown in figure. The particle with cavity now applies a gravitational force F2 on same particle placed at P. The radio F2/F1 will be
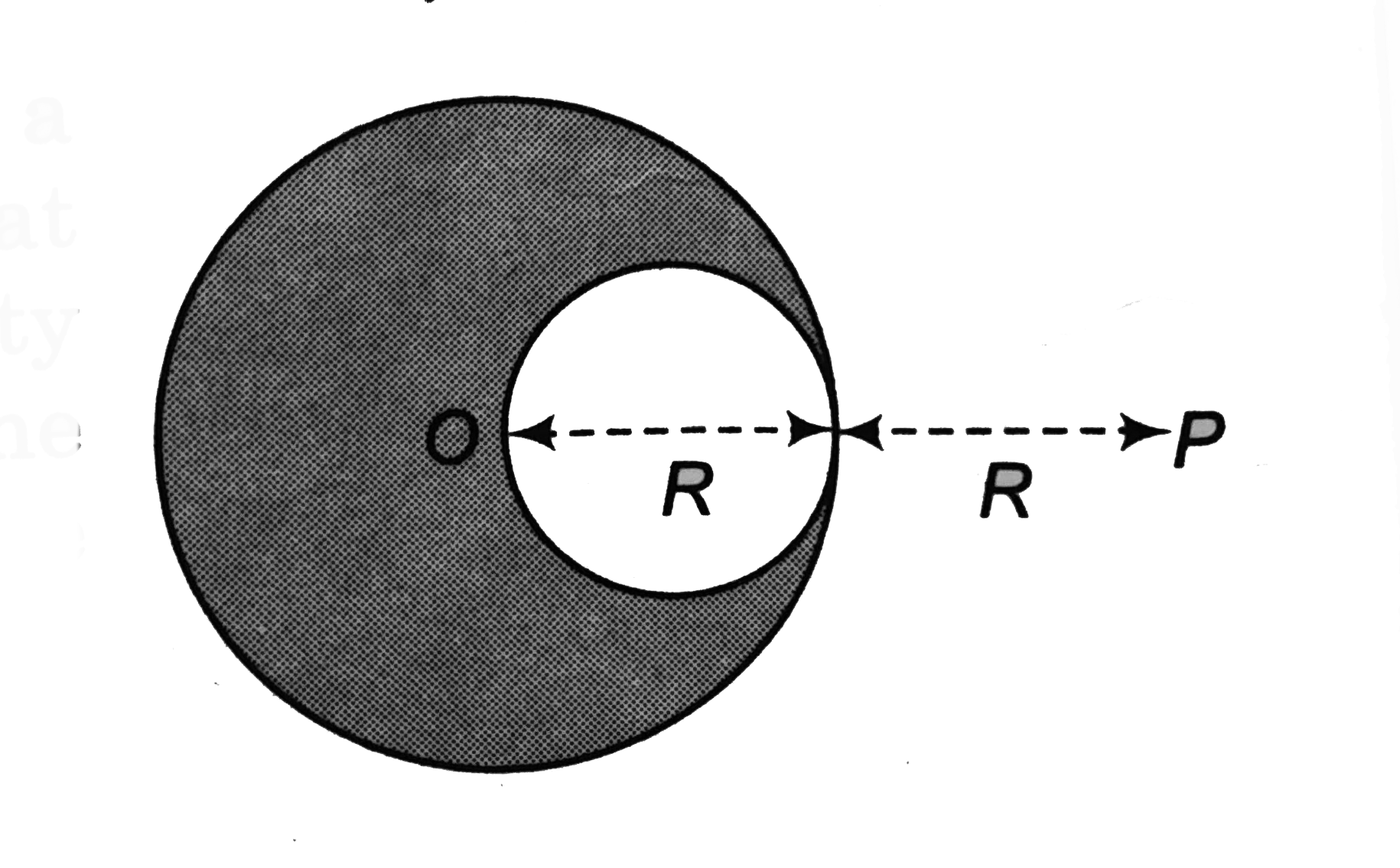 View Solution
View SolutionQuestion 307
According to Newton's law of gravitational, everybody in this universe attracts every other body with a force, which is directly proportional to the product of their masses and is inversely proportional to the square of the distance between their centres, i.e.,
F∝m1m2r2 or F=Gm1m2r2
where G is universal gravitational constant =6.67×10−11Nm2kg−2.
(i) What is the value of G on the surface of moon?
(ii) How is the gravitational force between two bodies affected when distance between them is halved?
(iii) What values of like do you learn from this law?View SolutionQuestion 308
Everybody, when free, falls towards the centre of earth with an acceleration =g, which is called acceleration due to gravity. The value of g on the surface of earth is, g=GMR2=9.8m/s2. It is a vector, directed always the centre of earth. The value of g does not depend upon shape, size or mass of the body. Rether, it depends on mass and size of earth (or planet due to which there is a gravity pull).
Read the above passesge and answer the following questions :
(i) A piece of stone and a feather are dropped together in space from the same height. which one will strike the ground first ? (ii) The mass of a planet is 18th the mass of earth and its diameter is 56 the diameter of earth. What is the value of 'g' on the surface of this planet.
(iii) What does the concept of free fall imply in day to day life?View SolutionQuestion 309
Whenever a body is thrown vertically upwards with a certain velocity, the upwards motion is opposed by gravitational pull of earth and resisatnce of air. The velocity of the body goes on decreasing at a constant rate (=−g).As soon as upward velocity of body becomes zero, it cannot rise any more. The height it has attained is the maximum height. The body then begins to fall downwards with an acceleration =g.
Read the above passege and answer the following questions :
(i) A body is thrown upwards with a velocity of 19.6m/s. What is the maximum height attained?
(ii) With what velocity will the body hit the ground?
(iii) What are the implications of this study in day to day life ? View SolutionQuestion 310
The escape velocity of a body from the surface of earth is the minimum velocity of projection of the body from the surface, which would take the body just beyound the gravitational field of earth. Once the body crosses the gravitational field of earth, it will never return to earth on its own. The body is said to have esacped. If M is mass of earth and R is radius of earth, then esacpe velocity,
Ve=√2GMR=√2gR. The value of Ve does not depend upon mass of the body.
Read the above passega and answer the following questions :
(i) What is the escape velocity from the surface of earth for a body of mass 2kg and for another body of mass 20kg? Is the energy required in the two cases same ?
(ii) What value of life do you learn from this study ?View SolutionQuestion 311
While studying the theory of planetary motion, kepler established three laws. According to kepler's second law, the line joining a planet to the sun sweeps out equal areas in equal intervals of time, i.e., the areal velocity of the planet around the sun is constant. This led him to conlude from the sun.
Read the above passege and answer the following questions :
(i) What is the basis of kepler's second law?
(ii) Mercury is closer to the sun than the earth. Will time period of mercury be less or more than one year ? Why ?
(iii) What value of life do you learn from kepler's second law?View Solution
All Exercises from PRADEEP PHYSICS (HINGLISH) Class 11 PHYSICS GRAVIATION
- ASSERTION-REASON TYPE QUESTIONS
- FILL IN THE BLANKS
- FOCUS MULTIPLE CHOICE QUESTIONS I.
- INTEGER TYPE QUESTIONS
- MULTIPLE CHOICE QUESTIONS
- MULTIPLE CHOICE QUESTIONS -II
- MULTIPLE CHOICE QUESTIONS II.
- MULTIPLE CHOICE QUESTIONS III.
- MULTIPLE CHOICE QUESTIONS IV.
- MULTIPLE CHOICE QUESTIONS V.
- NCRET MULTIPLE CHOICE QUESTIONS -I
- PROBLEMS FOR PRACTIVE
- PROBLEMS FOR PRACTIVE A
- PROBLEMS FOR PRACTIVE B
- PROBLEMS FOR PRACTIVE C
- PROBLEMS FOR PRACTIVE D
- PROBLEMS FOR PRACTIVE E
- PROBLEMS FOR PRACTIVE F
- PROBLEMS FOR PRACTIVE G
- PROBLEMS FOR PRACTIVE H
- PROBLEMS FOR PRACTIVE I
- PROBLEMS FOR PRACTIVE J
- PROBLEMS FOR PRACTIVE K
- ADDITIONAL EXERCISES
- ADVANCED PROBLEMS FOR COMPETITIONS
- CONCEPTUAL PROBLEMS
- CONCEPTUAL PROBLEMS I.
- CONCEPTUAL PROBLEMS II.
- CONCEPTUAL PROBLEMS III.
- CONCEPTUAL PROBLEMS IV.
- CONCEPTUAL PROBLEMS V.
- CURIOSITY QUESTION
- LONG ANSWER QUESTIONS
- NCERT
- QUESTIONS
- SAMPLE PROBLEM
- SHORT ANSWER QUESTIONS
- SHORT ANSWER QUESTIONS I.
- SHORT ANSWER QUESTIONS II.
- SHORT ANSWER QUESTIONS III.
- SHORT ANSWER QUESTIONS IV.
- SHORT ANSWER QUESTIONS V.
- SOLVED EXAMPLES
- SOLVED EXAMPLES TYPE A
- SOLVED EXAMPLES TYPE B
- SOLVED EXAMPLES TYPE C
- SOLVED EXAMPLES TYPE D
- SOLVED EXAMPLES TYPE E
- SOLVED EXAMPLES TYPE F
- SOLVED EXAMPLES TYPE G
- SOLVED EXAMPLES TYPE H
- SOLVED EXAMPLES TYPE I
- SOLVED EXAMPLES TYPE J
- SOLVED EXAMPLES TYPE K
- VALUE BASED QUESTIONS
- VERY SHORT ANS. QUESTIONS
- VERY SHORT ANS. QUESTIONS I.
- VERY SHORT ANS. QUESTIONS II.
- VERY SHORT ANS. QUESTIONS III.
- VERY SHORT ANS. QUESTIONS IV.
- VERY SHORT ANS. QUESTIONS V.
- VERY SHORT ANSWER QUESTIONS