SOLVED EXAMPLES TYPE E from PRADEEP PHYSICS (HINGLISH) SYSTEMS OF PARTICLES AND ROTATIONAL MOTION for Class 11
| Class 11 | PHYSICS |
| Chapter | SYSTEMS OF PARTICLES AND ROTATIONAL MOTION |
| PRADEEP PHYSICS (HINGLISH) | SOLVED EXAMPLES TYPE E |
| Medium | English |
| Academic Year | 2023-2024 |
Question 3
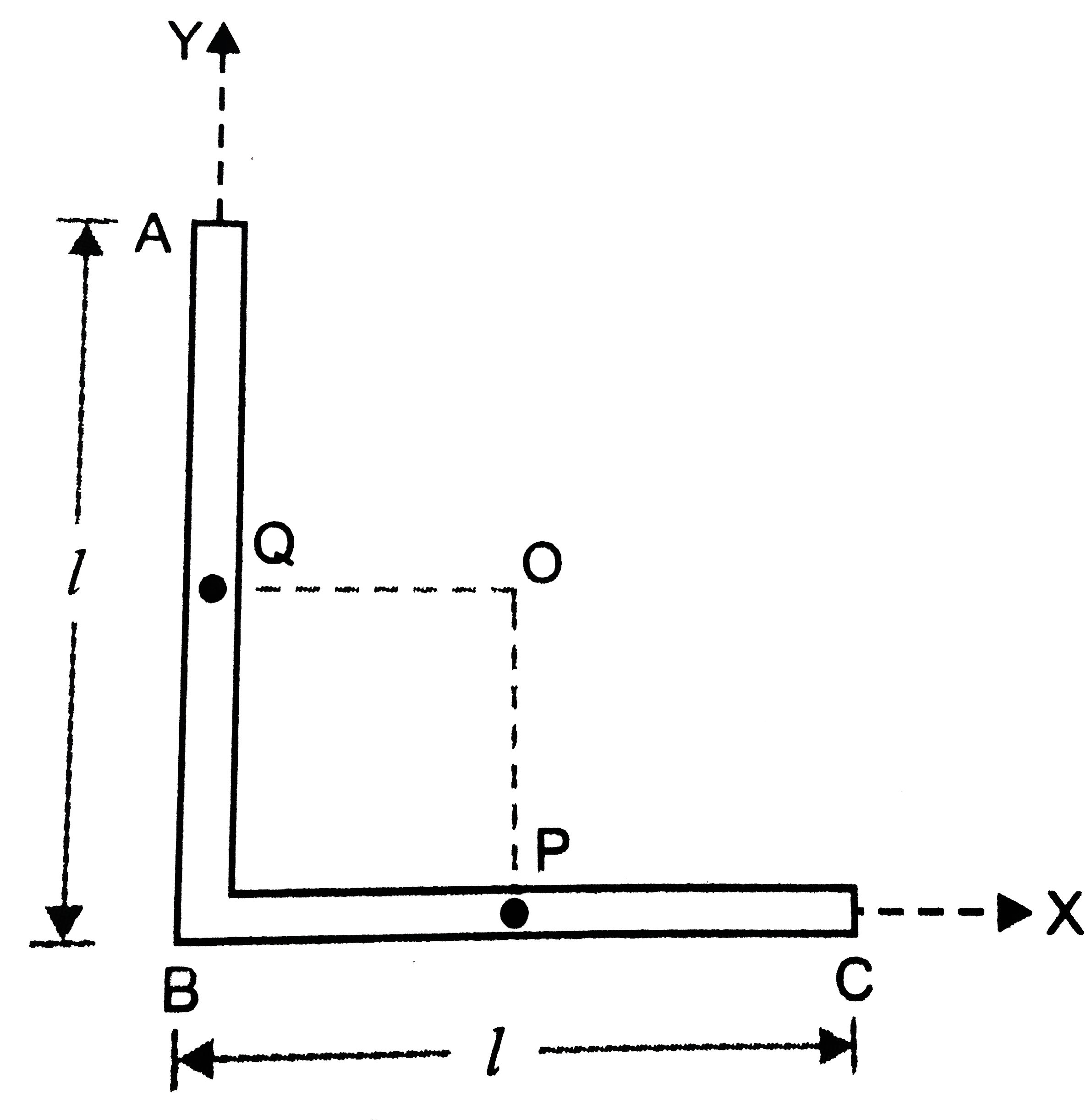
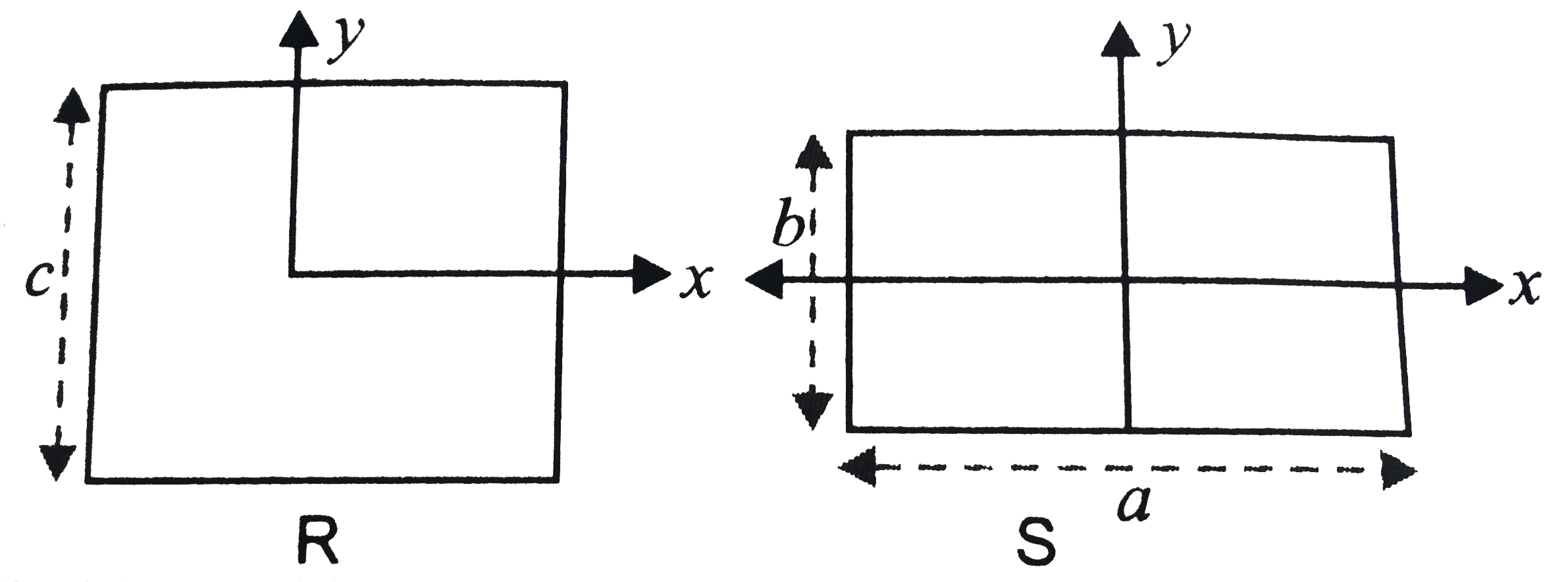
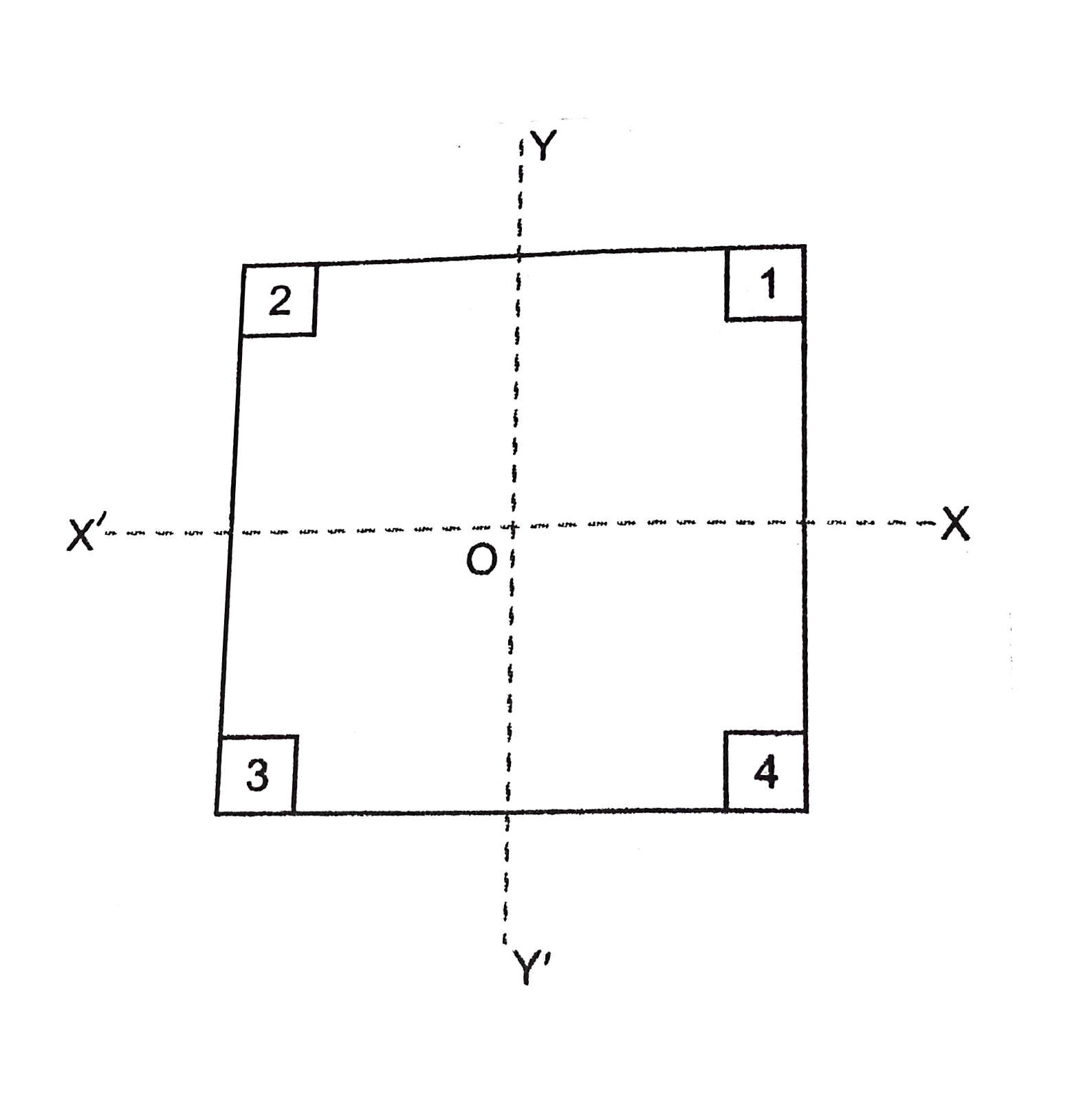
Fig. shown a uniform square plate from identical squares at the corners can be removed. (a) Where is the centre of mass of the plate originally ? (b) Where is it after square 1 is removed ?
(c ) where is it after squares 1 and 2 are removed ? (d) Where is c.m after squares 1,2,3, are removed ?
(f) Where is c.m after all the four squares are removed ? Answer in terms of quadrants and axes.
 View Solution
View SolutionQuestion 33
A dics rotates about the central axis starting from rest and accelerates with constant angular accelertion. At one time, it is rotating at 10rps , 60 revoluting later, its angular speed is 15rps. Calculate (i) angular acceleration (ii) time required to complate 60 revols (iii) the time required to reach 10rev/sec angular speed and (iv) number of revoluting from rest until the time the disc reaches 10rps angular speed.View SolutionQuestion 43
An insulated particle of mass m is moving in a horizontal plane (x - y) along X-axis. At a certain height above the ground, it suddenly explodes into two fragments of masses m/4and3m/4. An instant later, the smaller fragment is at Y=+15. The larger fragment at this instant is at :View SolutionQuestion 121
A flywheel of mass 25kg has a radius of 0.2m. It is making 240 rpm. What is the torque necessary to bring it to rest in 20s ? If the torque is due to a force applies tangentially on the rim of the wheel, what is the magnitude of the force ? Assume that mass of flywheel is concentrated at its rim.View SolutionQuestion 129
A cylinder of mass 5kg and radius 30cm and free to rotate about its axis receives an angular impulse of 3kgm2s−1 initially, followed by a similar impulse after every 4 second. What is the angular speed of the cylinder 30s after the initial impulse ? The cylinder is at rest initially.View SolutionQuestion 136
A preson is standing on the centre of a rotating table with his arms outstretched. The table is rotating freely with an angular his hands towards his chest. The moment of inertia reduces to 35 time the original moment of inertia. Calculate angular speed of the man when he withdraws his hands.View SolutionQuestion 147
A cylinder of mass 5kg and radius 30cm and free to rotate about its axis receives an angular impulse of 3kgm2s−1 initially, followed by a similar impulse after every 4 second. What is the angular speed of the cylinder 30s after the initial impulse ? The cylinder is at rest initially.View SolutionQuestion 149
A 70kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3m rotating about its verticle axis. The coefficient of friction between the wall and his clothing is 0.15 . What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed? View SolutionQuestion 152
A cord of negligible mass is wound round the rim of a flywheel of mass 20kg and radius 20cm. A steady pull of 25N is applied on the cord as shown in Fig. The flywheel is mounted on a horizontal axle with frictionless bearings.
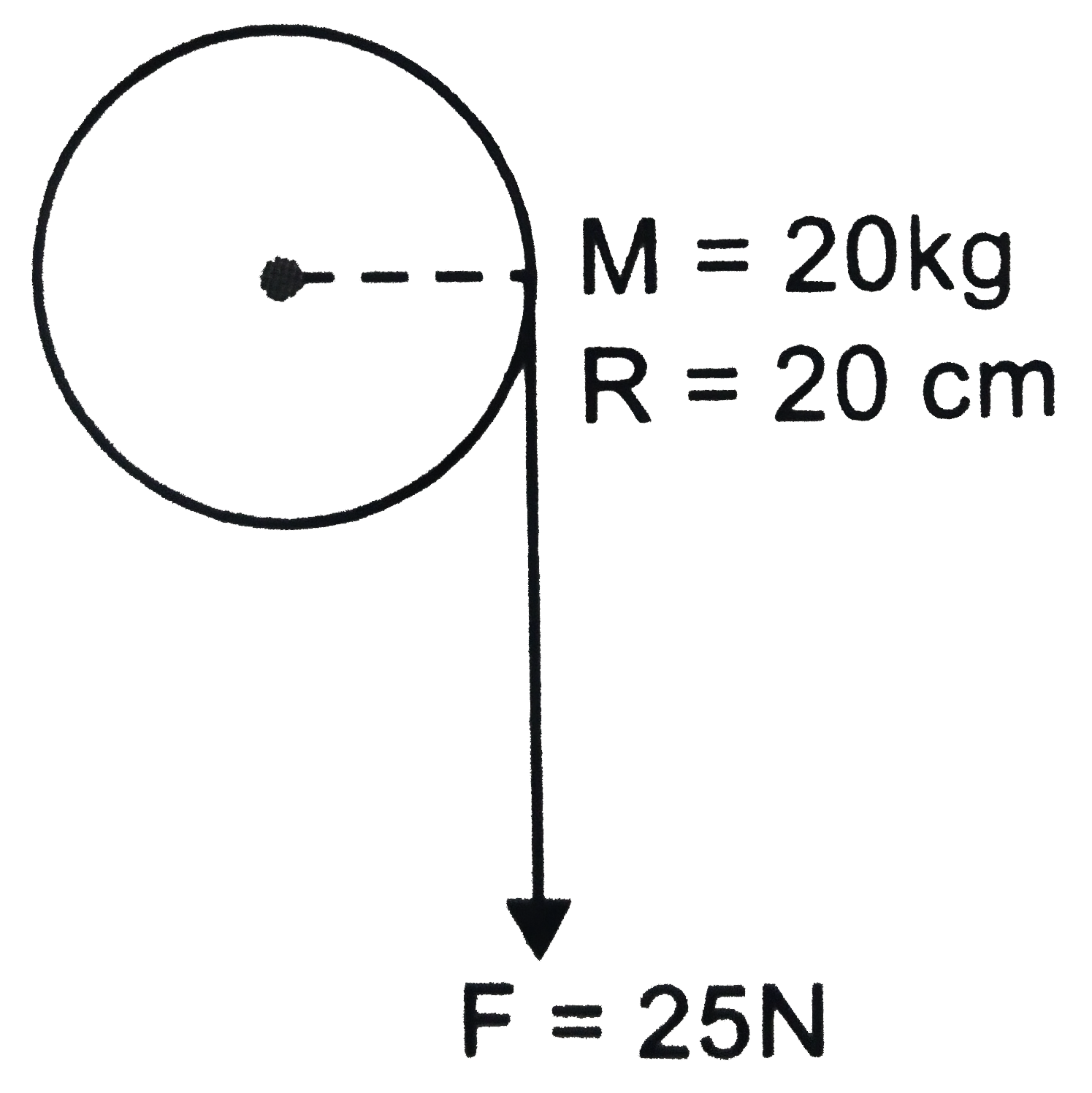
(a) Compute the angular acceleration of the wheel.
(b) Find the work done by the pull, when 2m of the cord is unwound.
(c) Find also the kinetic energy of the wheel at this point. Assume that the wheel stars from rest.
(d) Compare answers to parts (b)and (c).View SolutionQuestion 220
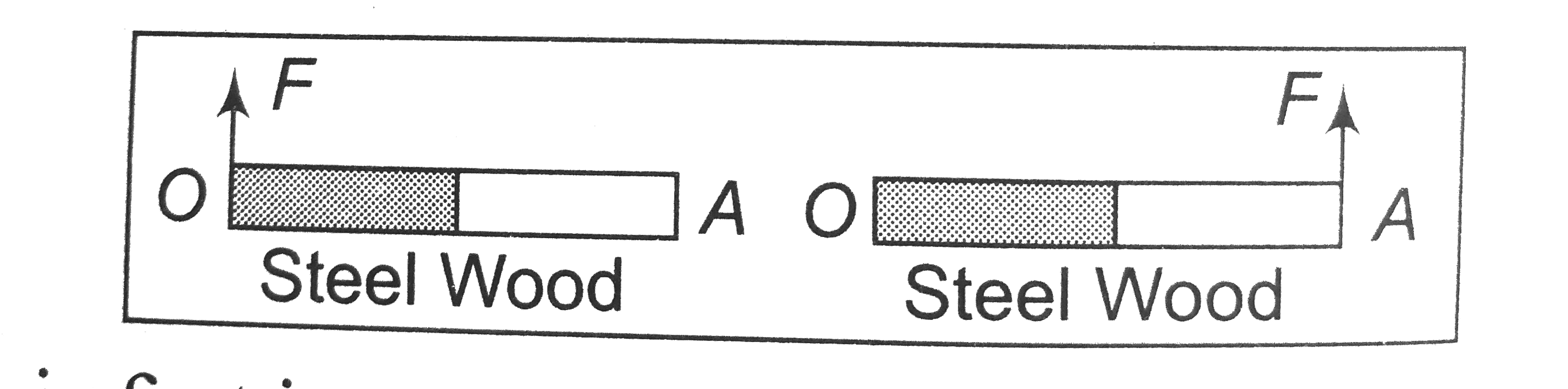
In first figure a meter stick, half of which is wood and the other half steel is pivoted at the wooden end at A and a force is applied at the steel and at O. On second figure the stick is pivoted at the steel end at O and the same force is applied at the wooden end at A. The angular acceleration.
 .View Solution
.View SolutionQuestion 227
A thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω. Another disc of the same dimensions but of mass M/4 is placed gently on the first disc co-axially. show that angular velocity o fthe system is 4ω/5.View SolutionQuestion 246
A 70kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3m rotating about its verticle axis. The coefficient of friction between the wall and his clothing is 0.15 . What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed? View SolutionQuestion 247
A solid cylinder at rest at top of an inclined plane of height 2.7m rolls down without slipping. If the same cylinder has to slide down a frictionaly inclined plane and acquires the same velocity as that acquired by centre of mass of rolling cylinder at the bottom of the incline, what should be the height of inclined plane ?View SolutionQuestion 253
A uniform bar of length 6a and mass 8m lies on a smooth horizontal table. Two point masses m and 2m moving in the same horizontal plane with speed 2v and v, respectively, strike the bar [as shown in the fig.] and stick to the bar after collision. Denoting angular velocity (about the centre of mass), total energy and centre of mass velocity by ω, E and vc respecitvely, we have after collison
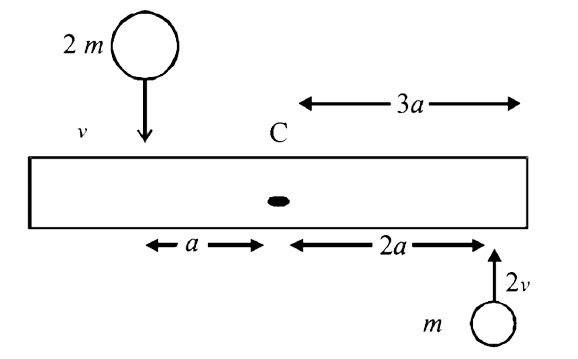 View Solution
View SolutionQuestion 259
A wheel of rdius r and moment of inertia I about its axis is fixed at top of an inclined plane of inclination θ as shownin figure. A string is wrapped round the wheel and its free end supports a block of mass M which can slide on the plane. INitialy, tehwheel is rotating at a speed ω in direction such that the block slides pu the plane. How far wil the block move before stopping? View Solution
View SolutionQuestion 260
A solid sphere of mass 3kg and radius 2m is free to rotate about an axis passing through its centre. Find a constant tangential force F required to rotate the sphere with a velocity of 10rad/s in 2sec. Starting from rest. Also, find the number of rotations made by the sphere in that time interval.View SolutionQuestion 261
Two discs of radii Rand2R are pressed against eachother. Initially, disc wit radius R is rotating with angular velocity ω and other disc is stationary. Both discs are hinged at their respective centres and are free to rotate about them. Moment of inertiaof smaller disc is I and of bigger disc is 2I about their respective axis of rotation. Find the angular velocity of bigger disc after long time.
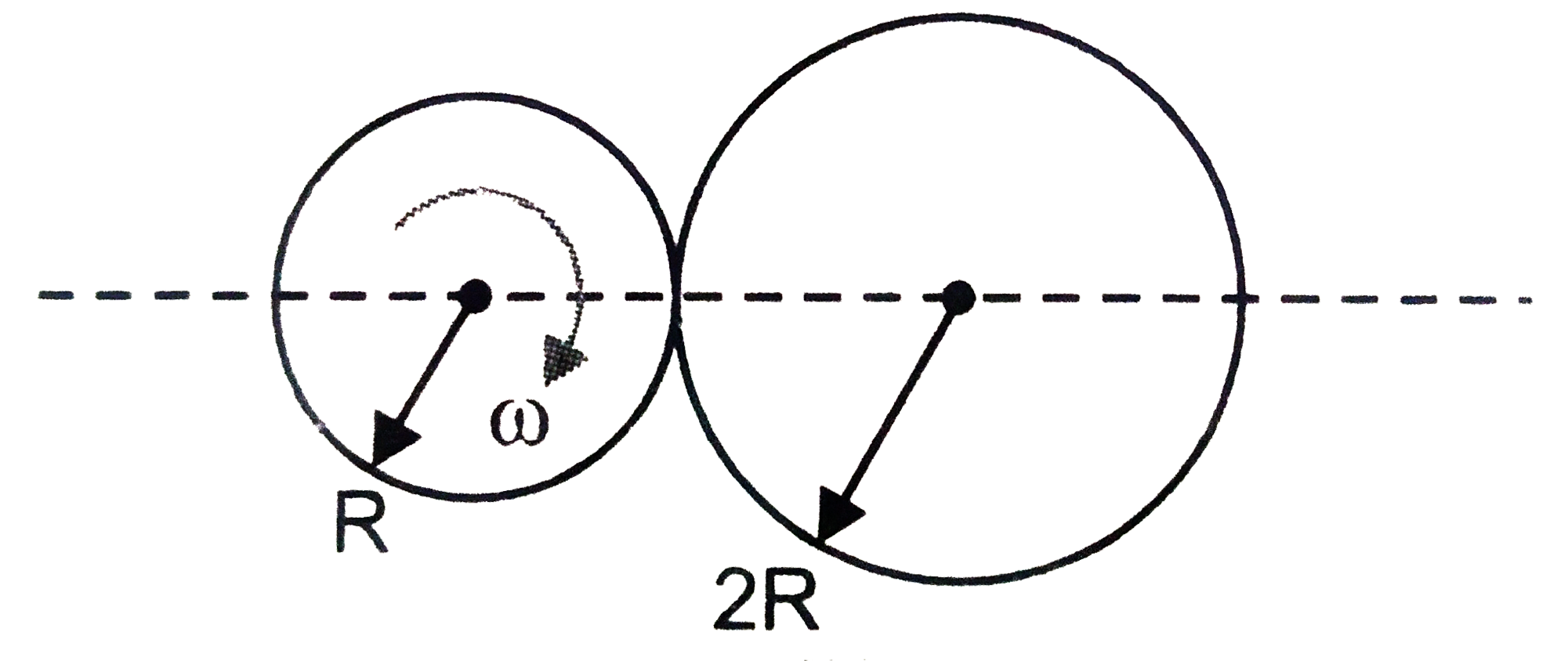 View Solution
View SolutionQuestion 265

A billiard ball, initially at rest, is given a sharp impulse by a cue. The cue is held horizontally a distance h above the centre line as shown in figure. The ball leaves the cue with a speed v0 and because of its backward slipping eventually acquires a final
speed 97v0 show that h=45R
Where R is the radius of the ball.View SolutionQuestion 267
In the HCI molecule, the separation between the nuclei of the two atoms is about 1.27Å(1Å=10−10m). Find the approximate location of the c.m of the molecule, given that a chorine atom ia about 35.5 times as massive as a hydrogen atom and nearly all the mass of an atom is cocentrated in its uncleus ?View SolutionQuestion 271
Find the components along the x,y,z axes of the angular momentum →L of a particle, whose position vector is →r with components x,y,z and momentum is →p with components px,pyandpz. Show that if the particle moves only in the x−y plane, the angular momentum has only a z-component.View SolutionQuestion 273
A non-uniform bar of weight W is suspended at rest by two strings of negligible weight as shown in Fig. The angles made by the strings with the vertical are 36.9∘and53.1∘ respectively. The bar is 2m long. Calculate the distance d of the centre of gravity of the bar from its left end.
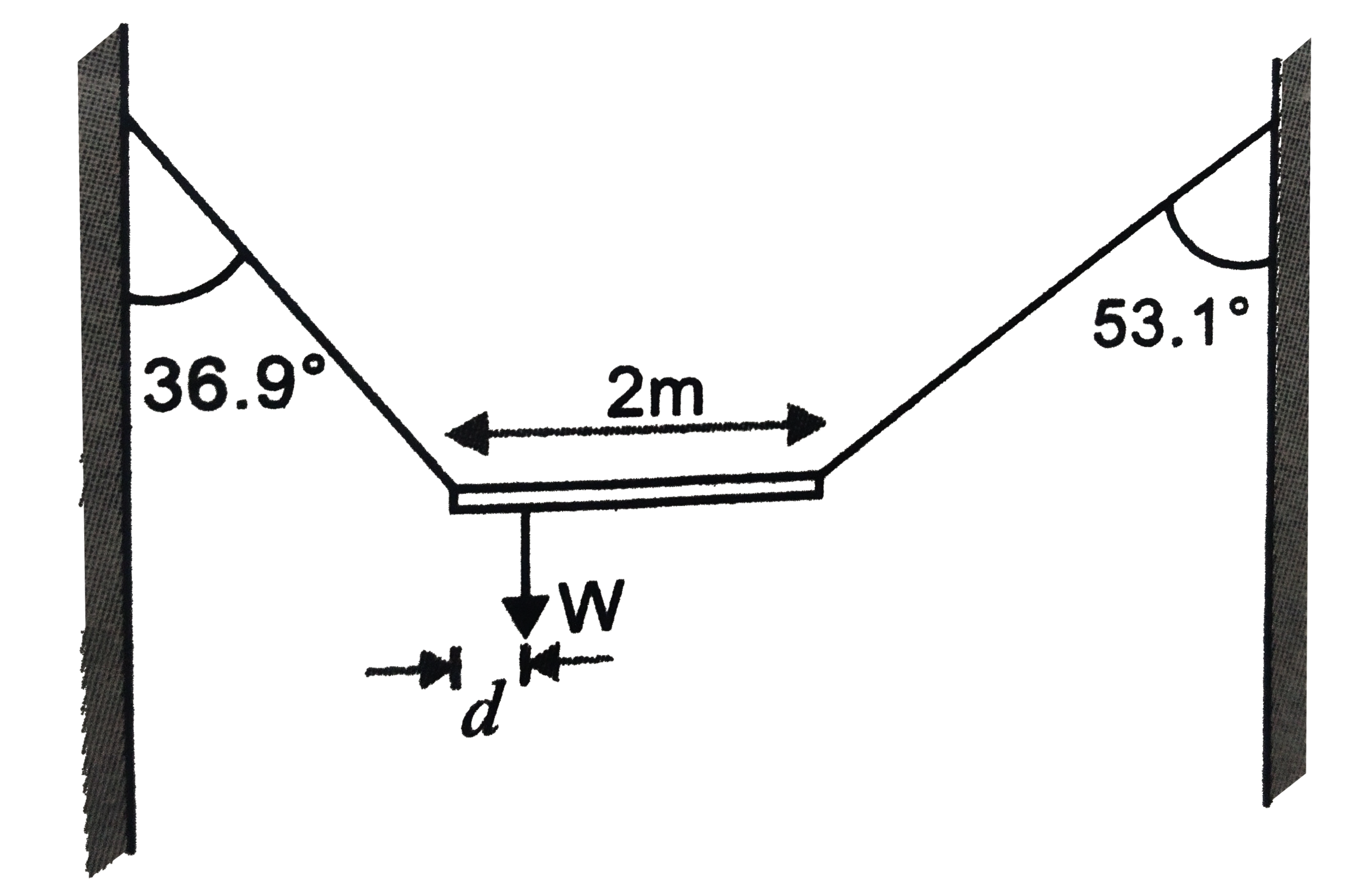 View Solution
View SolutionQuestion 275
(a) Find the moment of inertia of a sphere about a tangent to the sphere, given the moment of inertia of the sphere about any of its diameters to be 2MR2/5,whereM is the mass of the sphere and R is the radius of the sphere.
(b) Given the moment of inertia of a disc of mass M and radius R about any of its diameters to be 14MR2, find the moment of inertia about an axis normal to the disc passing through a point on its edge.View SolutionQuestion 276
Torques of equal magnitude are applied to hollow cylinder and a solid sphere, both having the same mass and same radius. The cylinder is free to rotate aabout its standard axis of symmetry, and the sphere is free to rotate about an axis passing through its centre. which of the two will aquire a greater angular speed after a given time ?View SolutionQuestion 278
A child stands at the centre of a turn table with his two arms outstretched. The turn table is set rotating with an angular speed of 40 rpm. How much is the angular speed of the child, if he folds his hands back reducing the moment of inertia to (2/5) time the initial value ? Assume that the turn table rotates without friction.
(b) Show that the child's new K.E. of rotation is more than the initial K.E. of rotation. How do you account for this increase in K.E. ?View SolutionQuestion 285
The oxygen molecule has a mass of 5.30×10−26kg and a moment of inertia of 1.94×10−46kgm2 about an axis through its centre perpendicular to the line joining the two atoms. Suppose the mean speed of such a molecule in a gas is 500m/s and that its kinetic energy of rotation is two thirds of its kinetic energy of translation. Find the average angular velocity of the molecule.View SolutionQuestion 287
As shown in Fig. the two sides of a step ladder BA and CA are 1.6m long and hinged at A. A rope DE,0.5m is tied half way up. A weight 40kg is suspended from a point F,1.2m from B along the ladderBA. Assuming the floor to be fricionless and neglecting the weight of the ladder, find the tension in the rope and forces exerted by the floor on the ladder. (Take g=9.8m/s2)
(Hint. Consider the eqilibrium of each side of the ladder separately.)
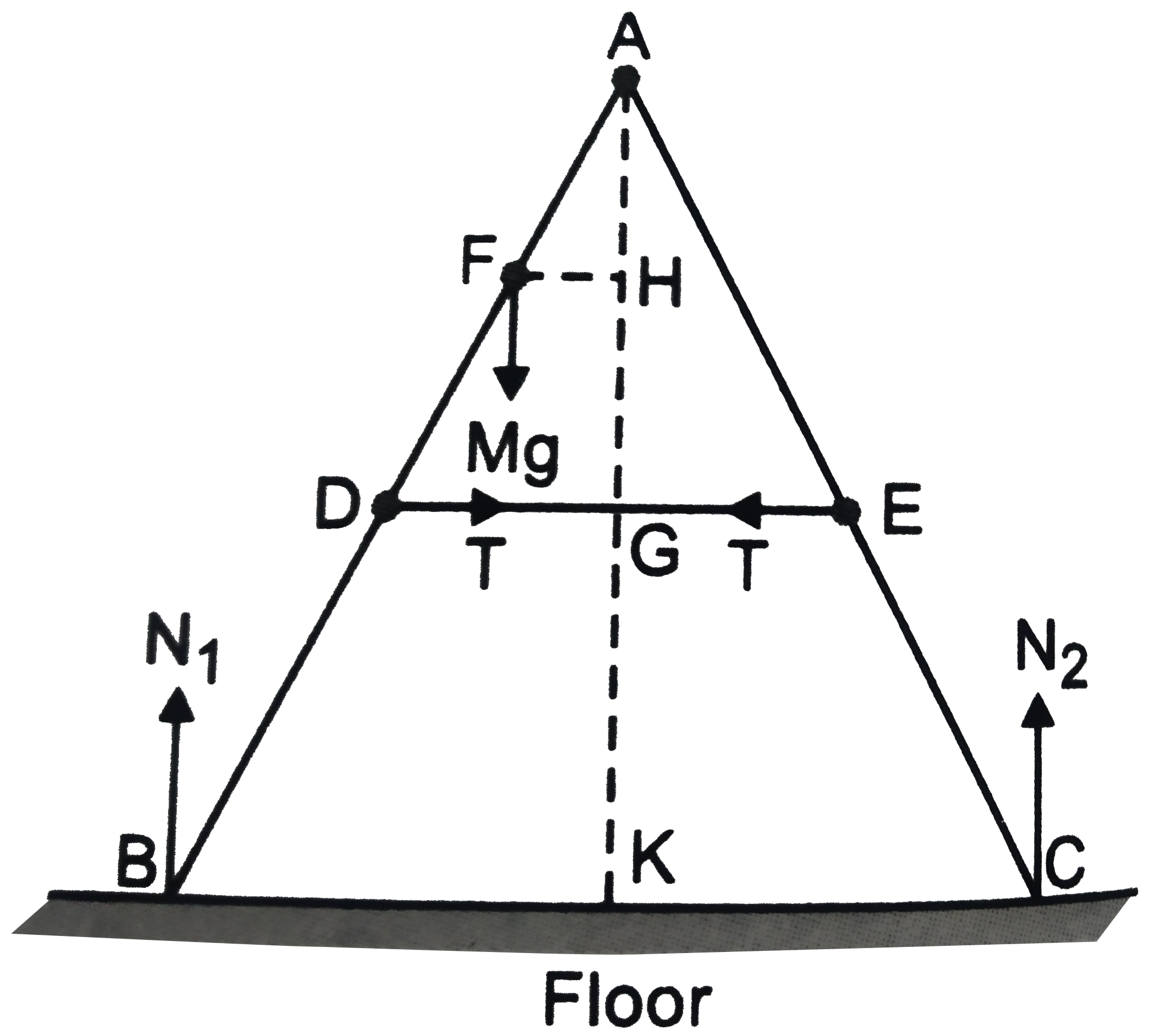 View Solution
View SolutionQuestion 288
A man stands on a rotating platform, with his arms stretched horizontal holding a 5kg weight in each hand. The angular speed of the platform is 30 revolutions per minute. The man then brings his arms close to his body with the distance of each weight from the axis changing from 90cm to 20cm. moment of inertia of the man together with the platform may be taken to be constant and equal t 7.6kgm2. (a) What is the his new angular speed ? (Neglect friction.)
(b) Is kinetic energy conserved in the process ? If not, from where does the change come about ?View SolutionQuestion 289
A bullet of mass 10g and speed 500m/s is fired into a door and gets embedded exactly at the centre of the door. The door is 1.0m wide and weight 12kg. It is hinged at one end and rotates about a vertical axis practically without friction. Find the angular speed of the door just after the bullet embeds into it.(Hint. The moment of inertia of the door about the vertical axis at one end is ML2/3)View SolutionQuestion 290
Two discs of moments of inertia I1andI2 about their respective axes (normal to the disc and passing through the centre) and rotating with angular speeds ω1andω2 are brought into contact face to face with their axes of rotation coincident.
(a) Does the law of conservation of angular momentum apply to the situation ? Why ?
(b) Find the angular speed of the two-disc system.
(c ) Calculate the loss in kinetic energy of the system in the process.
(d) Account for this loss.View SolutionQuestion 291
(a) Prove the theorem of perpendicular axes.
(Hint : Square of the distance of a point (x, y) in the x-y plane from an axis through the origin and perpendicular to the plane is (x2+y2).
(b) Prove the theorem of parallel axes.
(Hint : If the centre of mass of a system of n particles is chosen to be the origin ∑miri=0).View SolutionQuestion 292
Prove the result that the velocity v of translation of a rolling body (like a ring, disc, cylinder or sphere) at the bottom of an inclied plane of a hight h is given by v2=2gh(1+k2/R2) using dynamical consideration (i.e. by consideration of forces and torque). Note k i sthe radius of gyration of the body about its symmentry axis, and R is the radius of the body. The body starts from rest at the top of the plane.View SolutionQuestion 293
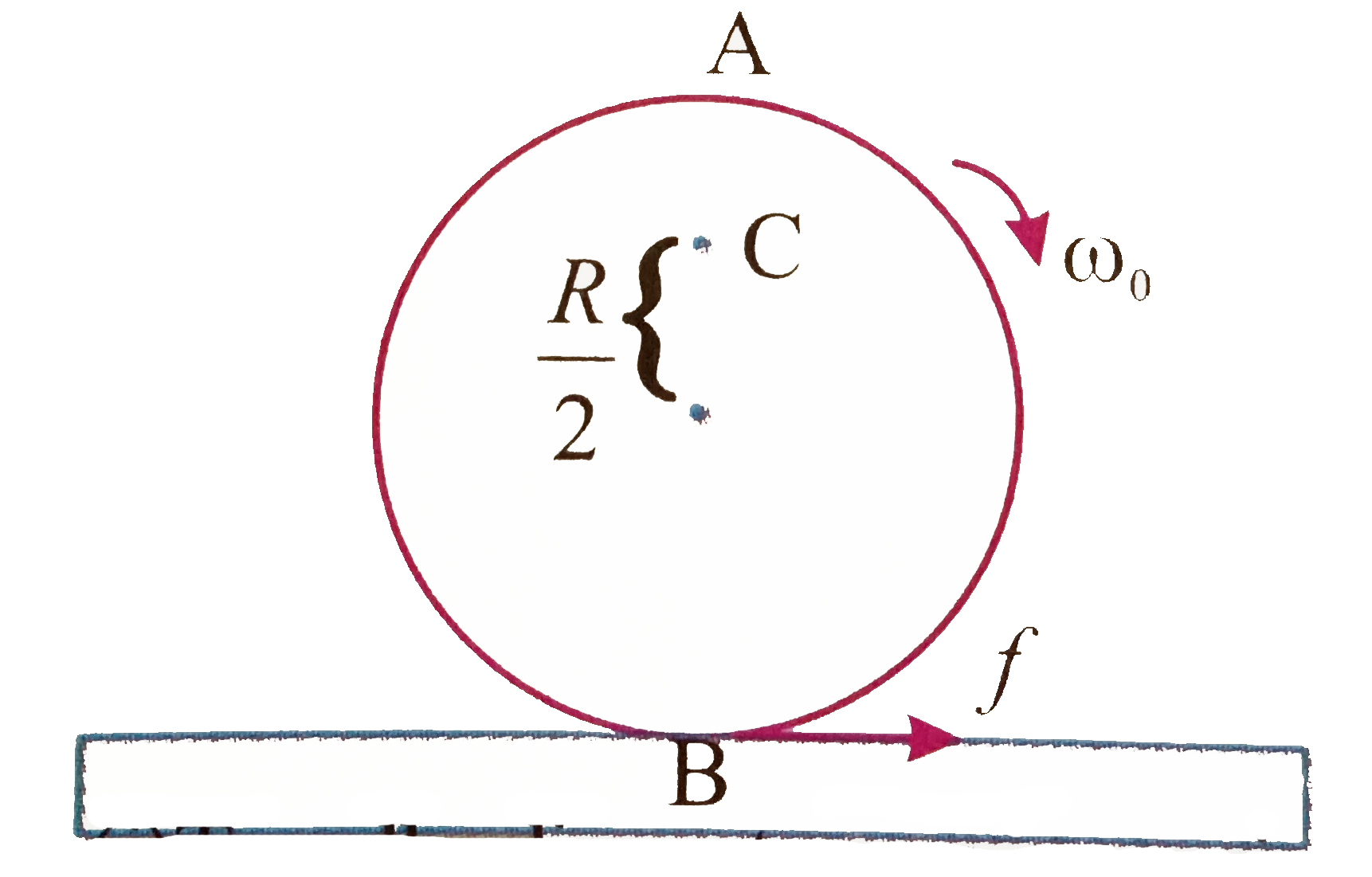
A disc roating about its axis with angular speed ω0 is placed lightly (without any translational pull) on a perfectly frictionless table. The radius of the disc is R. What are the linear velocities of the points A,BandC on the disc shown in Fig. Will the disc roll in the direction indicated ?
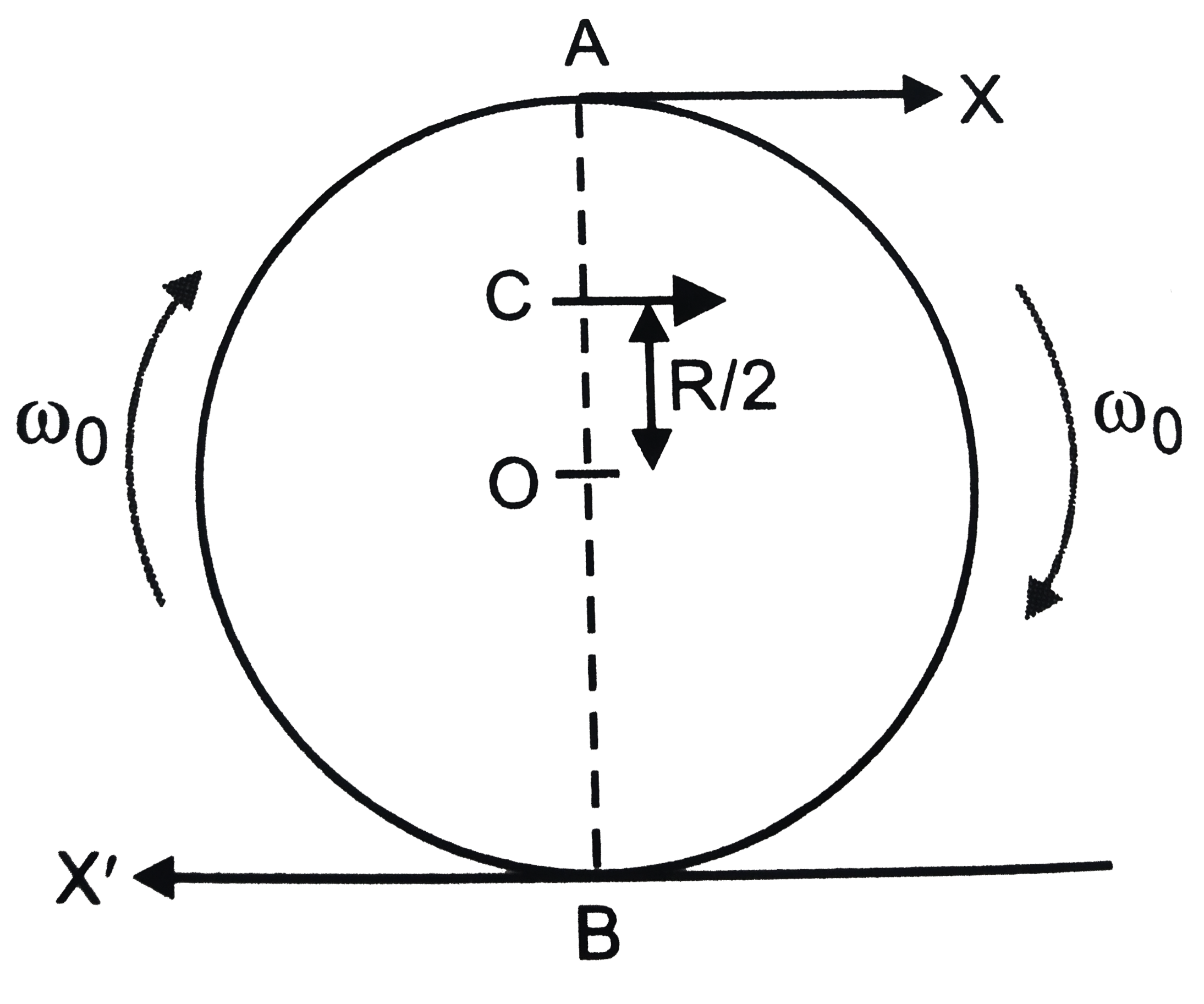 View Solution
View SolutionQuestion 296
A cylinder of mass 10kg and radius 15cm is rolling perfectly on a plane of inclination 30∘. The coefficient of static friction is μs=0.25.
(a) How much is the force of friction acting on the cylinder ?
(b) What is the work done against friction during rolling ?
(c ) If the inclination θ of plane is increased, at what value of θ does the cylinder begin to skid and not roll perfectly ?View SolutionQuestion 297
Read each statement below carefully and state with reasons, if it is true ot false. (a) During rolling the force of friction acts in the same direction as the direction of motion of c.m of the body. (b) The instantaneous speed of the point of contact during rolling is zero. (c ) The instantaneous acceleration of the point of contact during rolling is zero. (d) For perfect rolling motion, work done against friction is zero. (e) A wheel moving down a perfectly frictionless inclined plane will undergo slipping (not rolling motion).View SolutionQuestion 298
the centre of gravity of a body on the earth coincides with its centre of mass for a small object whereas for an extended object it may not ,what is the qualitaitve meaning of small and extended in this regard ?
for which of the following two coincides ? A building , a pond , a lake ,a mountain ?View SolutionQuestion 301
A unifrom cube of mass m and side a is placed on a frictionless horizontal surface. A vertical force F is applied to the edge as shown in Fig. Match the following (most appropriate choice) :
(a)mg/4<F<mg/2 (i) Cube will move up.
(b) F>mg/2 (ii) Cube will not exhibit motion.
(c ) F>mg (iii) Cube will begin to rotate and slip at A.
(d) F=mg/4 (iv) Normal reaction effectively at a/3 from A, no motion.
 View Solution
View SolutionQuestion 302
A uniform sphere of mass m and radius R is placed on a rough horizontal surface [Fig.] The sphere is struck horizontally at a hight h from the floor. Match the following :
(a) h=R/2 (i) Sphere rolls without slipping with a constant velocity and no loss of energy.
(b) h=R (ii) Sphere spins clockwise, loses energy by friction.
(c ) h=3R/2 (iii) Sphere spins anti-clockwise, loses energy by friction.
(d) h=7R/5 (iv) Sphere has only a translational motion, looses energy by friction.
 View Solution
View SolutionQuestion 304
A wheel in uniform motion about an axis passing through its centre and perpendicular plus is considered to be in mechanical (translational plus rotational ) equilibrium because no net external force or torqure is reqired to sustain its motion However , the particles than constitute the wheel do experience a centripeteal the acceleration wheel being in equilibrium ?
how would you set a half wheel into unifrom motion about an axis passing throgh the centre of mass of the wheel and perpendicular to its plane ? will ypu require external forces to sustain the motion ?View SolutionQuestion 308
Two discs of moments of inertia I1andI2 about their respective axes (normal to the disc and passing through the centre) and rotating with angular speeds ω1andω2 are brought into contact face to face with their axes of rotation coincident.
(a) Does the law of conservation of angular momentum apply to the situation ? Why ?
(b) Find the angular speed of the two-disc system.
(c ) Calculate the loss in kinetic energy of the system in the process.
(d) Account for this loss.View SolutionQuestion 309
A disc of radius R is rotating with an angular speed ω0 about a horizontal axis. It is placed on a horizontal table. The coefficient of kinetic friction is μk.
(a) What was the velocity of its centre of mass before being brought in contact with the table ?
(b) What happens to the linear velocity of a point on its rim when placed in contact with the table ?
(c ) What happens to the linear speed of the centre of mass when disc is placed in contact with the table ?
(d) Which force i sresponsible for the effects in (b) and (c ).
(e) What condition should be satisfied for rolling to begin ?
(f) Calculate the time taken for the rolling to begin.View SolutionQuestion 310
Two cylindrical hollow drums of radii Rand2R, and of a commom height h, are rotating with angular velocities ω (anti-clockwise) and ω (clockwise), respectively. Their axes, fixed are parallel and in a horizontal plane separated by (3R+δ). They are now brought in contact (δ→0).
(a) Show the frictional forces just after contact.
(b) Identify forces and torque external to the system just after contact.
(c ) What would be the ratio of final angular velocities when friction ceases ?View SolutionQuestion 316
A stone of mass m tied to the end of a string is whirled around in a horizontal circle (neglect force du eto grvaity). The length of the string is reduced gradually keeping the angular momentum of the stone about the centre of the circle constant. Then the tension in the given by T=Arn, where A is a constant and r is instantaneous radius of the circle. Show that n=−3.View SolutionQuestion 319
A solid cylinder of mass 20kg and radius 0.12m rotating wit initial angula speed of 125rad/s is placed lightly (i.e. without any translational push) on a horizontal table with coefficient of kinetic friction μk=0.15 between the cylinder and the table.
(a) After how long does the cylinder start rolling ?
(b) What is the initial translational energy, rotational energy and total energy of the cylinder ?
(c) What is the final (i.e. after rolling begins) translational energy, rotational energy and total energy of the cylinder ? (d) Is the finl total enrgy equal to the initial total energy of motion of the cylinder ? If not, where does the difference of energy disappear ?
(e) Account for the loss of total energy of motion in the following way : find the work done by friction on the body its translational motion. Show that net work done by friction on the body is negative, equal in magnitude to the loss of total energy calculated in (d) above.View SolutionQuestion 320
Point masses m1andm2 are placed at the opposite ends of a rigid rod of length L, and negligible mass. The rod is to be set rotating about an axis perpendicualr to it. The position of point P on this rod through which the axis should pass so that the work required to set the rod rotating with angular velocity ω0 is minimum, is given by :
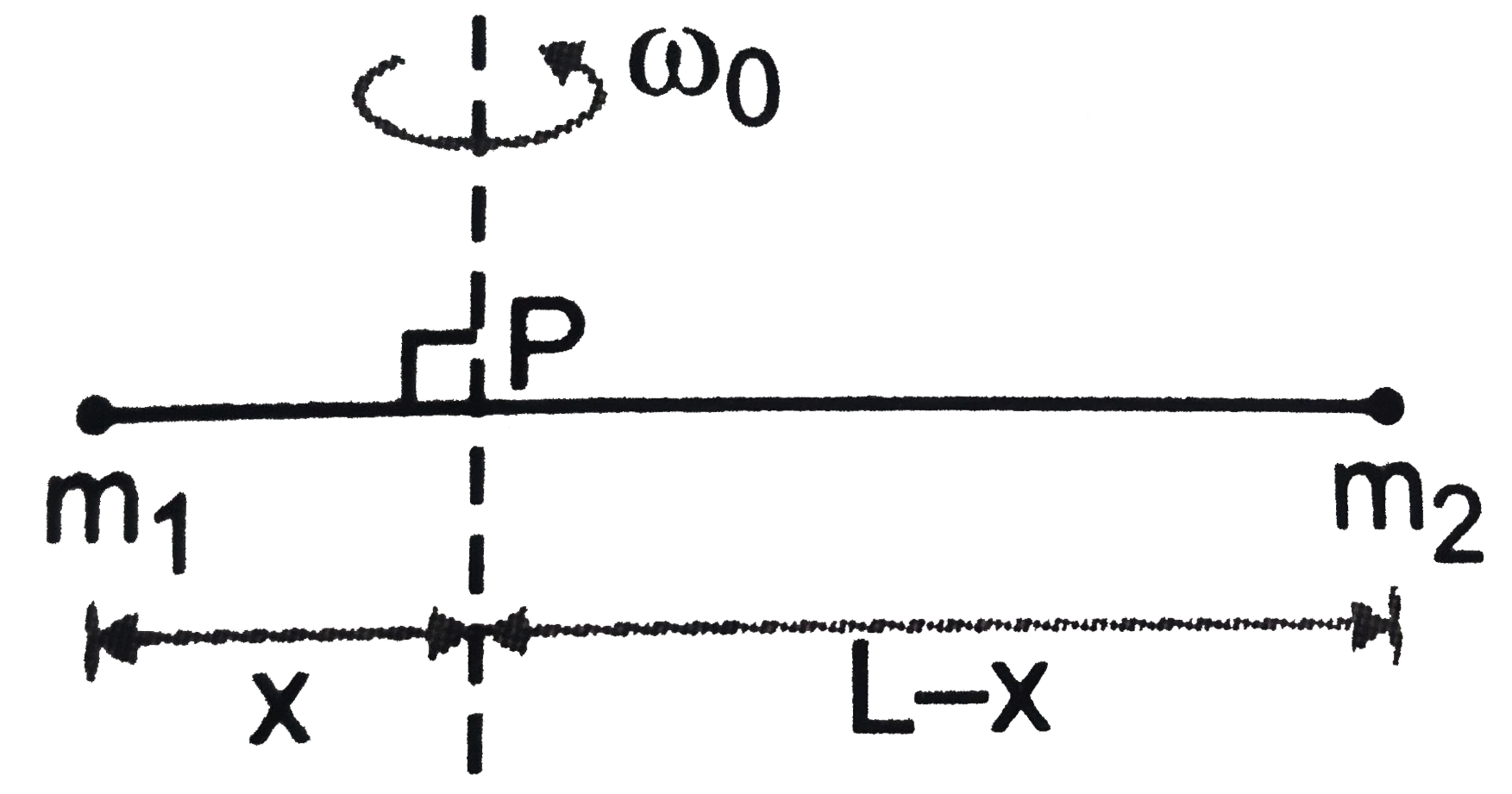 View Solution
View SolutionQuestion 321
A ball of mass 10−2kg and having charge +3×10−6C is tied at one end of a 1m along thread. The other end of the thread is fixed and a charge −3×10−6C is placed at this end. The ball can move in the circulr orbit of radius 1m in the vertical plane. Initially, the ball is at the bottom. Find the monimum initial horizontal velocity of the ball, so that it will be able to complete the full circle.View SolutionQuestion 322
Three particles, each of the mass m are situated at the vertices of an equilateral triangle of side a. The only forces acting on the particles are their mutual gravitational forces. It is desired that each particle moves in a circle while maintaining the original mutual separation a. Find the initial velocity that should be given to each particle and also the time period of the circular motion. (F=Gm1m2r2) View SolutionQuestion 325
A nail is located at a certain distance vertically below the point of suspension of a simple pendulum. The pendulum bob is released from a position where the string makes an angle of 60∘ with the vertical. Calculate the distance of nail from the point of suspension such that the bob will just perform revolutions with the nail as centre. Assume the length of the pendulum to be one meter.View SolutionQuestion 327
A carpet of mass M is rolled along its length so as to from a cylinder of radius R and is kept on a rough floor. When a negligibly small push is given to the cylindrical carpet, it stars unrolling itself without sliding on the floor. Calculate horizontal velocity of cylindrical part of the carpet when its radius reduces to R/2.View SolutionQuestion 328
The mechanical energy (E) of a body is the sum of kinetic energy (K) and potential energy (V) of the body i.e., E=K+V. Whereas K is always positive, V can be positive or negative. For a system to axis, K=(E−V)≥0
Negative value of E indicates a bound state. For example, all planets revolving around the sum have negative mechanical energy.
Read the above passage and answer the following questions :
(i) When mechanical energy E=0, does it mean K=0andV=0 ?
(ii) What is the implication of this study in day to day life ?View SolutionQuestion 329
The torque (τ) due to a force gives us the turning effect of the force about a fixed point/axis. It is measured by the product of magnitude of force (F) and perpendicular distance (r) of the line of action of force form the axis of rotation.
→τ=→r×→F=rFsinθˆn
where thete is smaller angle between →r and ˆn is unit vector along →τ.
Read the above passage and answer the following questions :
(i) What is the significance of torque ?
(ii) How do you determine the direction of torque ?
(ii) What is the implication of this concept in day to day life ?View SolutionQuestion 330
A rigid body is said to be in translational equilibrium, if it remains at rest or moving with a constant velocity in a particular direction. For this, the net external force or vector sum of all the external forces acting on the body must be zero, i.e.,
→F=0or→F=∑→Fi=0
If U is potential energy of the body, then
F=−dUdr=0orU= constant (max. or min.)
When U= minimum, equilibrium of body is stable,
When U tends to increase, equilibrium is unstable,
When U remains constant, equilibrium is neutral.
Read the above passage and answer the following questions :
(i) When can a body moving uniformly along a straight line be in equilibrium ? What is this equlilbrium called ?
(ii) What is the significance of U= minimum in day to day life ?View SolutionQuestion 331
When a compass needle is held arbitrarily in any direction in earth's magnetic field, a couple acts on the needle. The force on north pole of needle is towards the north and force on south pole of the needle is towards south. These forces are equal in magnitude and opposite in direction. They from a couple, which rotates the compass needle and aligns it along north south direction. Once the alignment is complete, net force and net torque on the compass needle reduce to zero.
Read the above passage and answer the following :
(i) What is the origin of force and torque on the compass needle ?
(ii) What values of life do you learn from this study ?View SolutionQuestion 332
The concept of centre of mass proves that laws of mechanics which are true for a point mass, are equally valid for all macroscopic bodies of any shape, size, mass, etc. For example, when vector sum of external forces acting on a system of particles is zero, the velocity of centre of mass of the system will remain constant.
Read the above passage and answer the following questions :
(i) Is centre of mass of a body a real point ?
(ii) Does centre of mass lie within the body always ?
(iii) How do you justify that −−→vcm= constant ?View Solution
All Exercises from PRADEEP PHYSICS (HINGLISH) Class 11 PHYSICS SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- ASSERTION- REASON TYPE QUESTIONS
- FILL IN THE BLANKS
- FOCUS MULTIPLE CHOICE QUESTIONS I.
- INTEGER TYPE QUESTIONS
- MULTIPLE CHOICE QUESTIONS
- MULTIPLE CHOICE QUESTIONS COMPREHENSION 2
- MULTIPLE CHOICE QUESTIONS II.
- MULTIPLE CHOICE QUESTIONS III. COMPREHENSION 1
- MULTIPLE CHOICE QUESTIONS-I
- MULTIPLE CHOICE QUESTIONS-II
- PROBLEMS FOR PRACTICE
- PROBLEMS FOR PRACTICE TYPE A
- PROBLEMS FOR PRACTICE TYPE B
- PROBLEMS FOR PRACTICE TYPE C
- PROBLEMS FOR PRACTICE TYPE D
- PROBLEMS FOR PRACTICE TYPE E
- ADDITIONAL EXERCISES
- ADVANCED PROBLEMS FOR COMPETITIONS
- CONCEPTUAL PROBLEMS
- CONCEPTUAL PROBLEMS I.
- CONCEPTUAL PROBLEMS II.
- CURIOSITY QUESTIONS
- LONG ANSWER QUESTIONS
- NCERT
- QUESTIONS
- SAMPLE PROBLEM
- SHORT ANSWER QUESTIONS
- SHORT ANSWER QUESTIONS I.
- SHORT ANSWER QUESTIONS II.
- SOLVED EXAMPLES
- SOLVED EXAMPLES TYPE A
- SOLVED EXAMPLES TYPE B
- SOLVED EXAMPLES TYPE C
- SOLVED EXAMPLES TYPE D
- SOLVED EXAMPLES TYPE E
- VALUE BASED QUESTIONS
- VERY SHORT ANSWER QUESTIONS
- VERY SHORT ANSWER QUESTIONS I.
- VERY SHORT ANSWER QUESTIONS II.