Molecules And Crystals from IE IRODOV PHYSICS Chapter 1 ATOMIC AND NUCLEAR PHYSICS for Class 12
| Class 12 | PHYSICS |
| Chapter | ATOMIC AND NUCLEAR PHYSICS |
| IE IRODOV PHYSICS | Molecules And Crystals |
| Medium | English |
| Academic Year | 2023-2024 |
Question 5
Show that the frequency intervals between the neighbouring spectral lines of a true ratational spectrim of a diatomic molecules are equal. Find the moment of intertial and the distance between the nuclei of a CH molecule if the intervals between the neighbouring lines of the true rotational spectrum of these molecules are equal to Δω=5.47.1012s−1View SolutionQuestion 6
For an HF molecule find the number of rotational levels located between the Zeroth and first excited vibrational levels assuming rorational states to be independent of vibrational ones. The natural vibration frequency of this molecule is equal to 7.79.1014rad/s and the distance between the nuclie is 91.7pm.View SolutionQuestion 8
Find the number of ratational levels per unit energy interval, dN/dE, for a diatomic molecule as a function of rotational energy E. Calculate of an magnitude for an iodine molecule in the state with rotational quantum number J=10. The distance between the nuclei of that molecule is equal to 267pm.View SolutionQuestion 9
Find the ratio of energies required to excite a diatomic molecule to the first vibrational and to the first rotational level.
Calculate that ratio for the following molecules:
Molecule, ω,1014s−1 d, pm
(a) H28.374
(b) HI4.35160
(c ) I2040267
Here ω is the natural vibration frequency of a molecule, d is the distance between nuclei.View SolutionQuestion 10
The natural vibration frequency of a hydrogen molecule is equal to 8.25.1014S−1, the distance between the nuclei is 74pm, Find the ratio of the number of these molecules at the first excited vibrational level (v=1) to the number of molecules at the first excited rotational level (J=1) at a temperature T=875K. It should be remembered that degeneracy of rotational levels is equal to 2J+1.View SolutionQuestion 11
Derive Eq. (6.4c), making use of the Boltzmann distribution. From Eq.(6.4c) obtain the expression for molar vibration heat capacity CV vib of diatomic gas. Calculate CV vib for cl2 gas at the temperature 300K. The natural vibration frequency of these molecules is equal to 1,064.1014s−1.View SolutionQuestion 15
Find the ratio of intensities of the voilet and red satellites closest to the fixed line, in the vibraiton sopecturm of Raman scattering by Cl2 molecule at a temperature T=300K if the natural Vibration frequency of these molecules is ω=1.06.1014s−1,. By what factor will this ratio change if the temperature is doubled?View SolutionQuestion 20
Assuming the propagation velocities of longitudinal and transverse vibrations to be the same and equal to v, find the Debye temperature
(a) for a unidimensional crystal, i.e., a chain identical atoms, incorporating n0 atoms per unit length,
(b) for a two-dimensional crystal, i.e., a plance square grid consisting of identical atoms, containing n0 atoms per unit area,
(c ) for a simple cubic lattice consisting of identical atoms, containing n0 atoms per unit volume.View SolutionQuestion 24
In a chain of identical atoms the vibration frequency ω depends on wave number kas ω=ωmaxsin(ka/2), where ωmax is the maximum vibration frequency ω, a is the distance between neighbouring atoms. Making use of this dispersion relation, find the dependence of the number of longitudinal vibrations per unit. frequency interval on ω i.e., dN/ω, if the length of the chain is l. Having obtained dN/ω, find the total number N of possible longitudinal vibrations of the chain.View SolutionQuestion 26
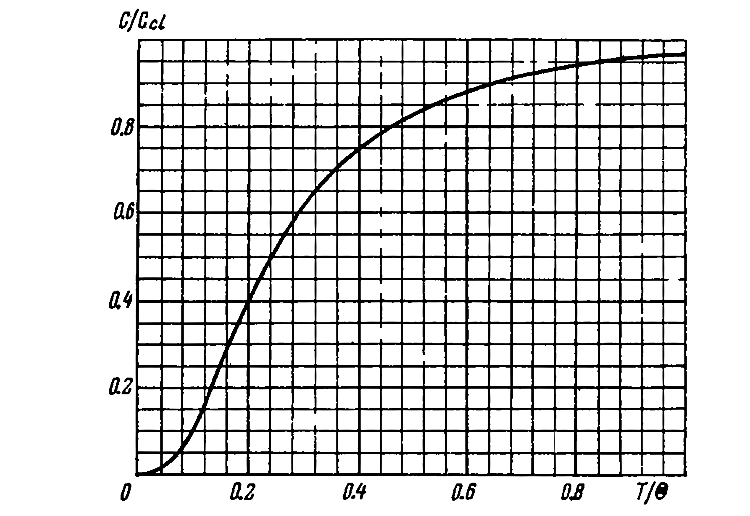
Figure. 6.10 shows heat capacity of a crystal vs temperatue in terms of the Debye theory. Here Ccl is classical heat capacity Θ is the Debye temperature. Using this plot, find:
(a0 The Debye temperature for silver if at a temperature T=65K its molar heat capacity is equal to 15J(mol.K),
(b) the molar heat capacity of aluminum at T=80K if at T=250K it is equal to 22.4J(mol.K)
(c )the maximum vibration frequency for copper whose heat capacity at T=125K differs form the classical value by 25%.
 View Solution
View SolutionQuestion 45
The resostivity of an impurity-free semiconductor at room tempterature is ρ=50Ωcm. It becomes equal to ρ1=40Ωcm. When the semiconductor is illuminated with light, and t=8ms after swithching off the light source the resistivity becomes equal to ρ2=45Ωcm. Find the mean lifetime of conduction electrons and holes.View SolutionQuestion 46
In Hall effect measurements a plate of width h=10mm and length l=50mm made of p-type semiconductor was placed in a magnetic field with induction B=5.0kG. A potential difference V=10V was applied across the edges of the plate. In this case the hall field is VH=50mV and resistivity ρ=2.5Ω,cm. Find the concentration of holes and hole mobility.View SolutionQuestion 47
In a Hall effect measurements in magnetic field with induction B=5.0kG the transverse electric field strength in an impurity-free germanium turned out be η=10 times less than the longitudinal electric field strength. Find the difference in the mobilities of conduction electrons and holes in the given semiconductor.View Solution