The given two fixed rings of radius R lie in XY plane as shown in the figure. Linear charge density of the rings A and B varies as per the relationλ=λ0sinθ and λ=λ0cosθ respectively where theta is measured from +x axis. Distance between the centre of the two rings is r>>R
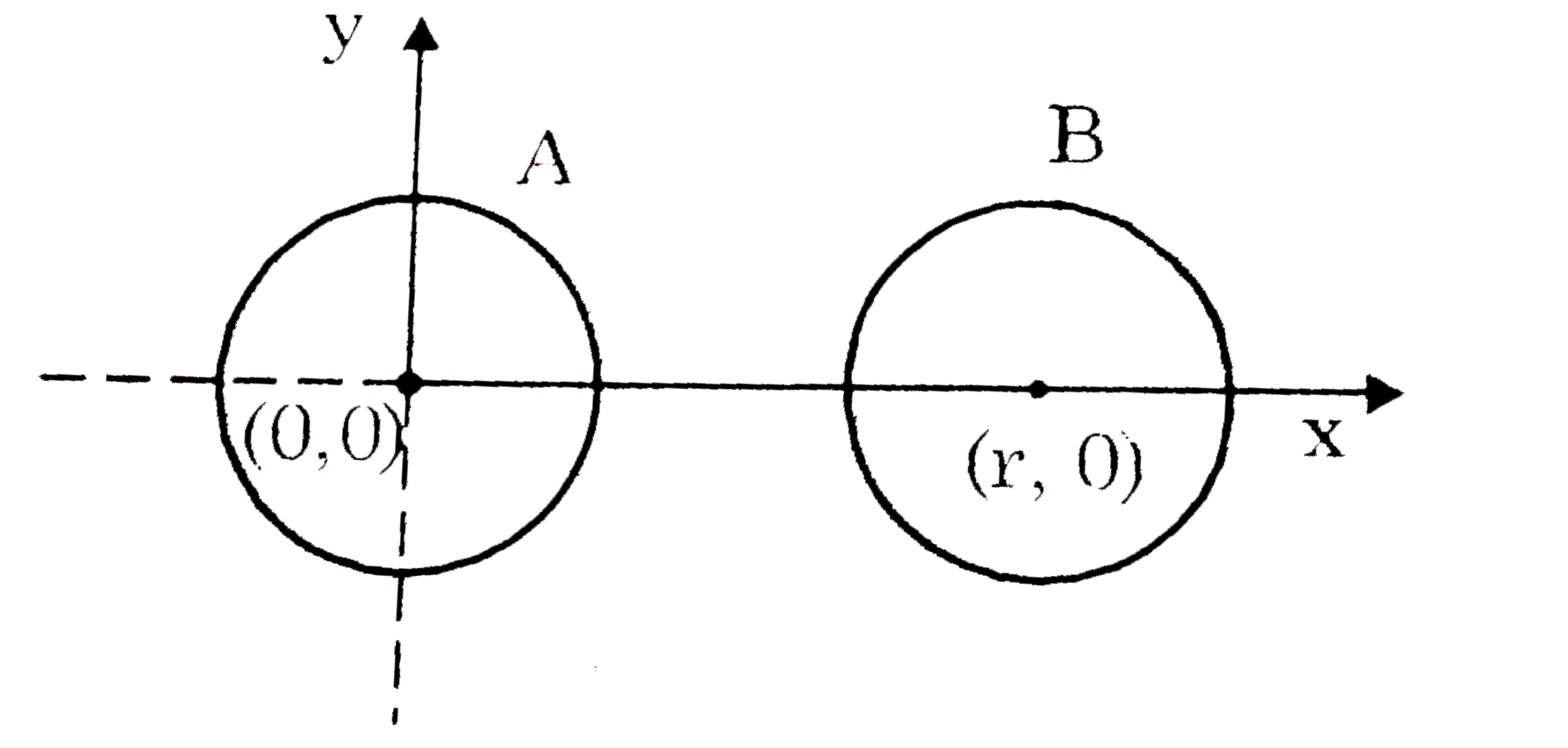
Force of interaction between the two ring is34×λ20π∈0(Rr)4
Force of interection between the two rings is32×λ20π∈0(Rr)4
Potential energy of interaction between the two ring of πλ20R44ε0r3
Potential energy of interaction between the two ring is zero.
The correct Answer is:A, D
∫dp=∫dq(2Rsinθ)
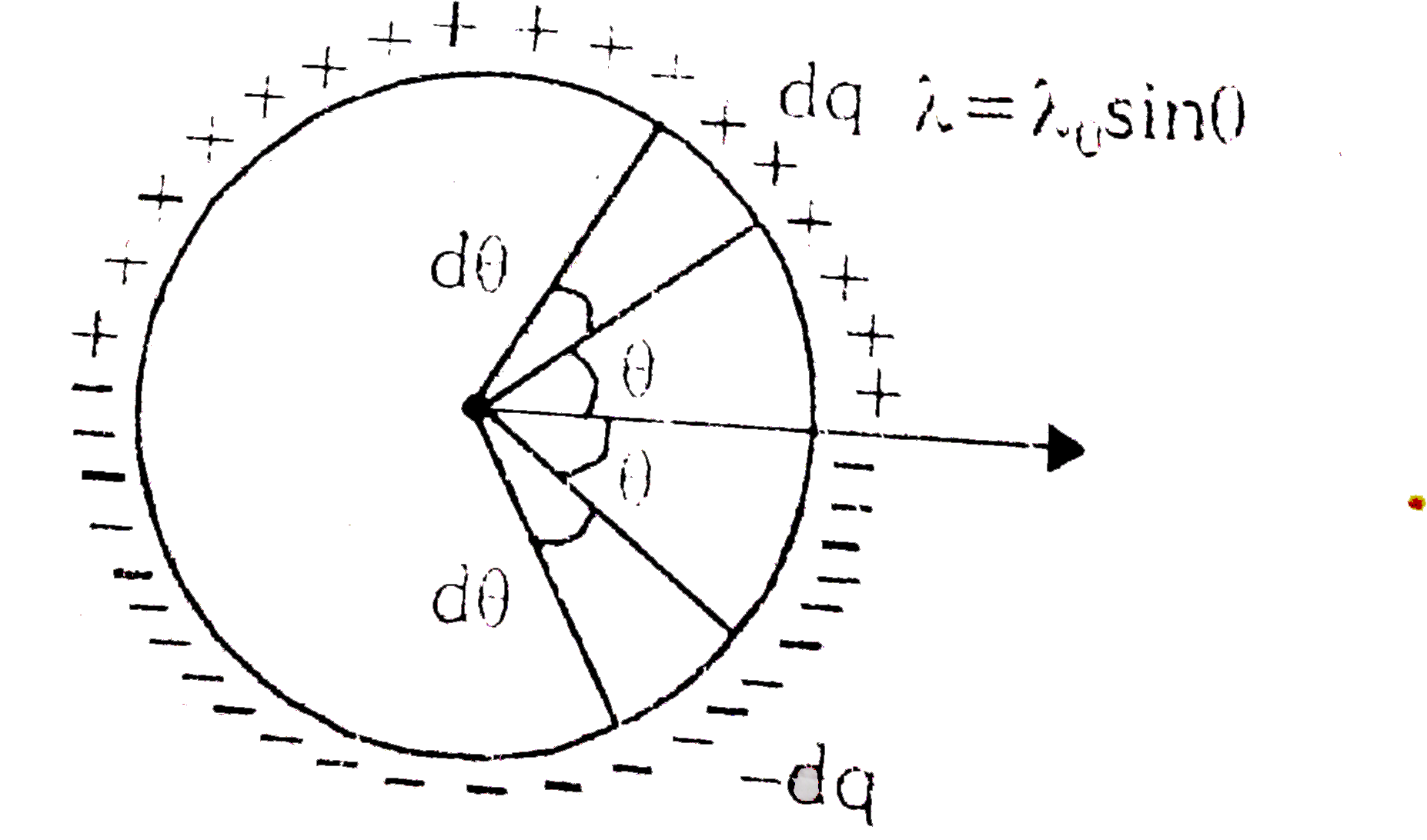
p=π∫0(λ0sinθ×Rdθ)(2Rsinθ)
p=πλ0R2 .....(i)
F=3kp2r4
=3λ20πR44ε0r4 .....(ii)
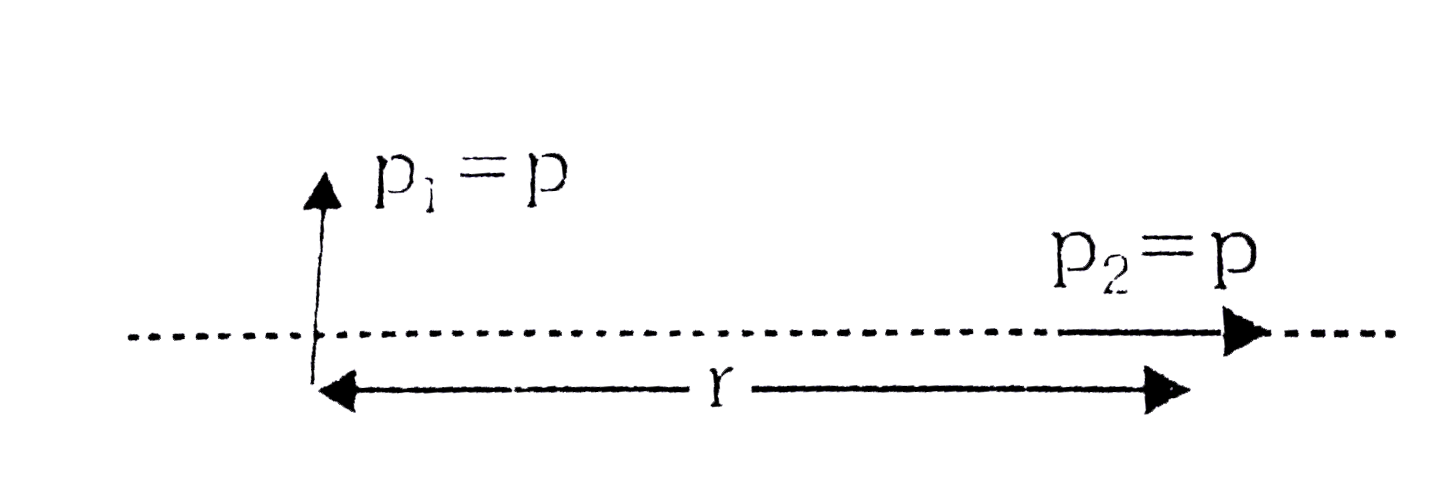
U=−P2E1cos90∘=0 ......(iii)
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - part-2 physic48videos
TEST PAPERS
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PHYSICS18videos
TEST PAPERS
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - Part-1 Physics15videos
TEST PAPERS
- BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS45videos
TEST PAPER 4
- BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)7videos
UNIT & DIMENSIONS, BASIC MATHS AND VECTOR
Similar Questions
Potential on the axis of ring of radius 3R and at distance 4R from centre of ring is (charge on the ring is Q )
View SolutionThe linear charge density on a dielectric ring of radius R vanes with θ as λ=λ0cosθ/2, where λ0 is constant. Find the potential at the center O of the ring [in volt].
View Solution
Knowledge Check
- Question 1 - Select One
The linear charge density on a ring of radius R is λ=λ0sin(θ) where λ0 is a constant and θ is angle of radius vector of any point on the ring with x-axis. The electric potential at centre of ring is
 A0Bλ0∈0Cλ0π∈0Dλ02π∈0
A0Bλ0∈0Cλ0π∈0Dλ02π∈0 - Question 2 - Select One
A semicircular wire is uniformly charged with linear charge density dependent on the angle θ from y-direction as λ=λ0|sinθ|, where λ0 is a constant. The electric field intensity at the centre of the arc is
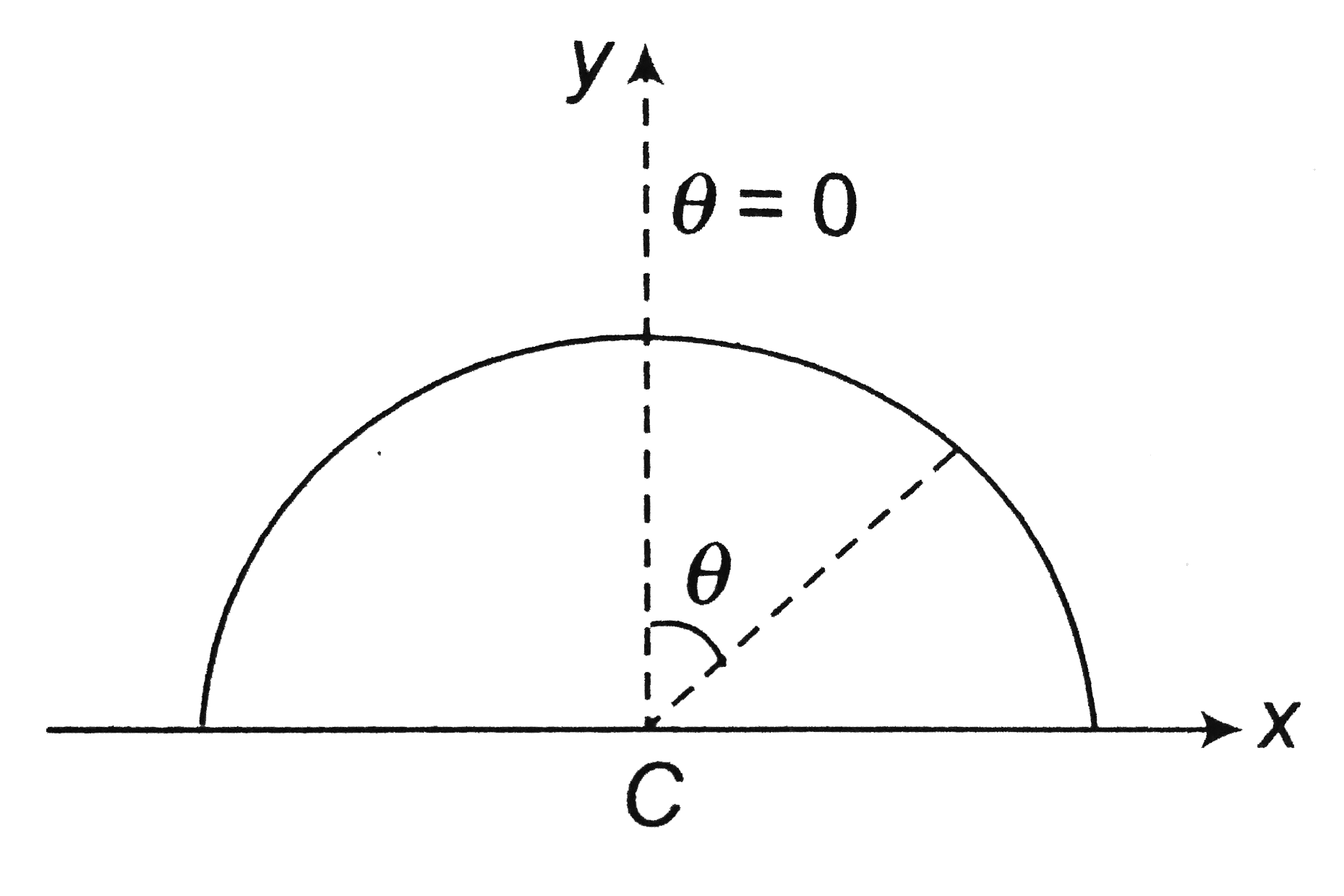 Aλ02πε0R(−ˆj)Bλ04πε0R(−ˆj)Cλ06πε0R(−ˆj)Dλ02√2πε0R(−ˆj)
Aλ02πε0R(−ˆj)Bλ04πε0R(−ˆj)Cλ06πε0R(−ˆj)Dλ02√2πε0R(−ˆj) - Question 3 - Select One
the linear charge density of a thin metallic rod varies with the distance x from the end as λ=λ0x2(0≤x≤l) The total charge on the rod is
Aλ0l33Bλ0l34C2λ0l33Dλ0l32
The linear charge density of a uniform semicircular wire varies with θ shown in the figure as λ=λ0cosθ if R is the radius of the loop ,of the charge on the wire is
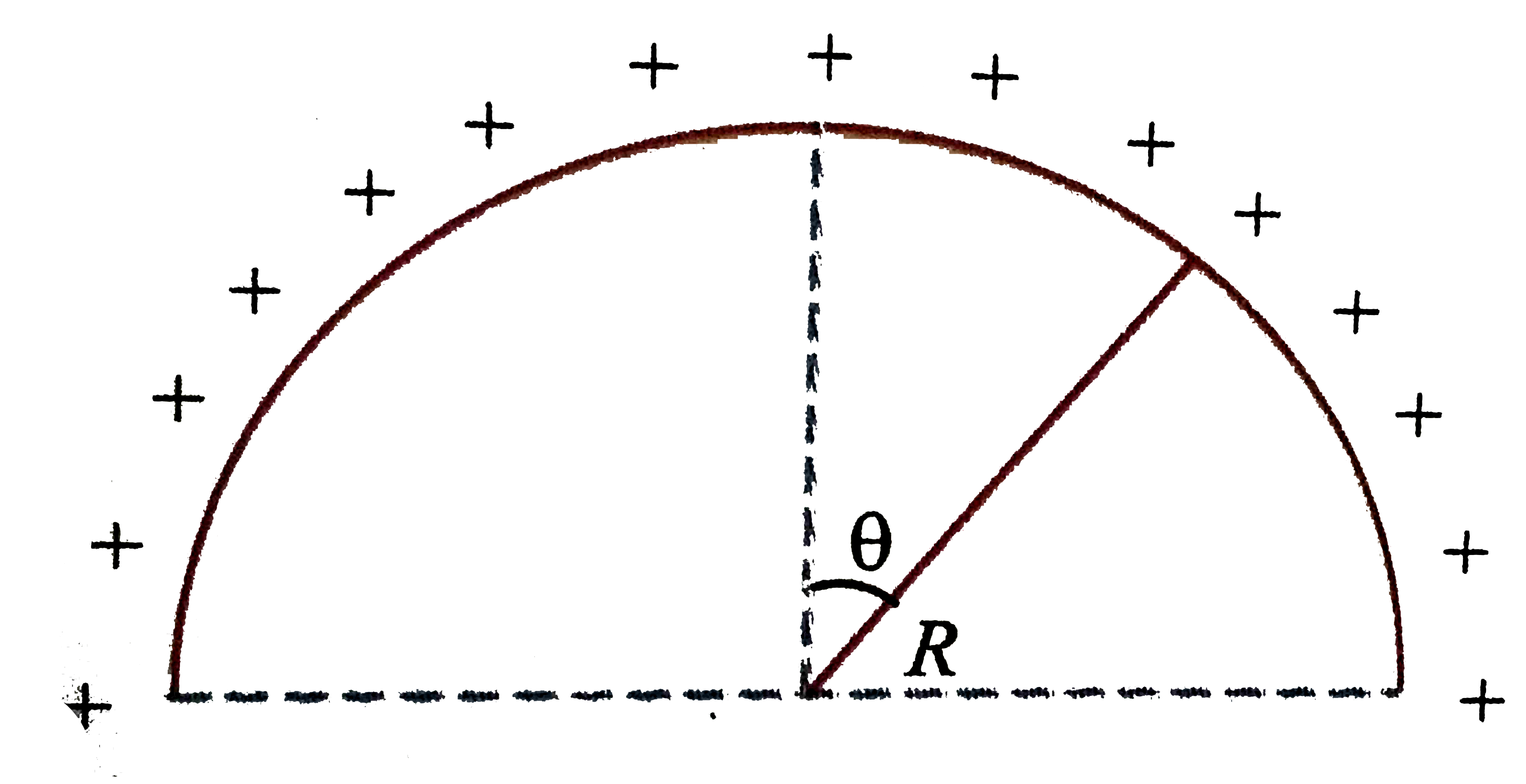 View Solution
View SolutionA thin non-conducting ring of radius R has a linear charge density λ=λ0cosθ, where θ is measured as shown. The total electric dipole moment of the charge distribution is
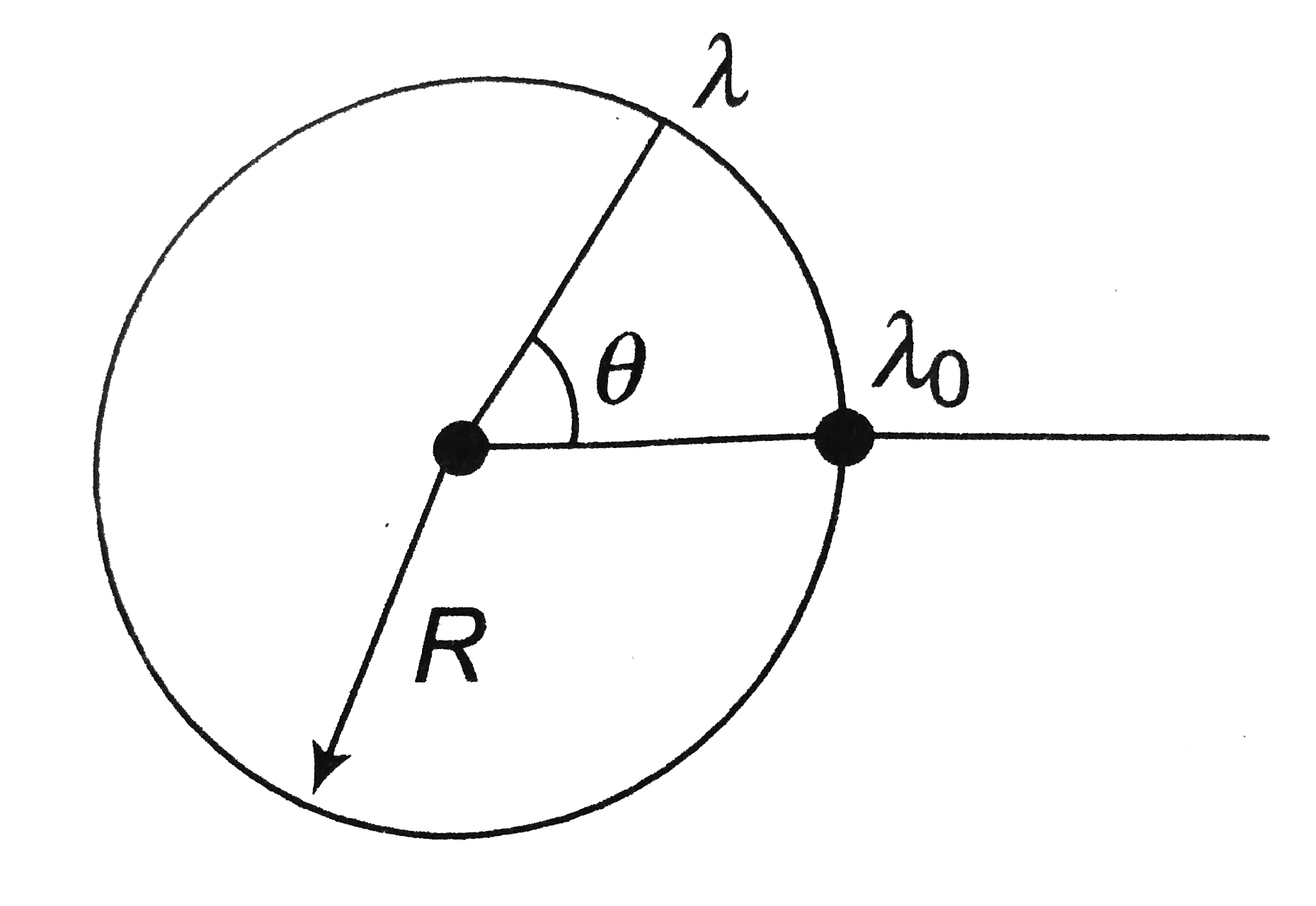 View Solution
View SolutionTwo thin wire rings each having a radius R are placed at a distance d apart with their axes coiciding. The charges on the two rings are +q and −q. The potential difference between the centres of the two rings is
View SolutionA fixed ring of radius R is given a charge q. A charge q0 is brought slowly from infinity to the centre of the ring. The wrong statement is-
View SolutionFor the hemisphere of radius R shown in the figure the surface charge density σ varies with θ (shown in figure) as σ=σ0cosθ the total charge on the sphere is
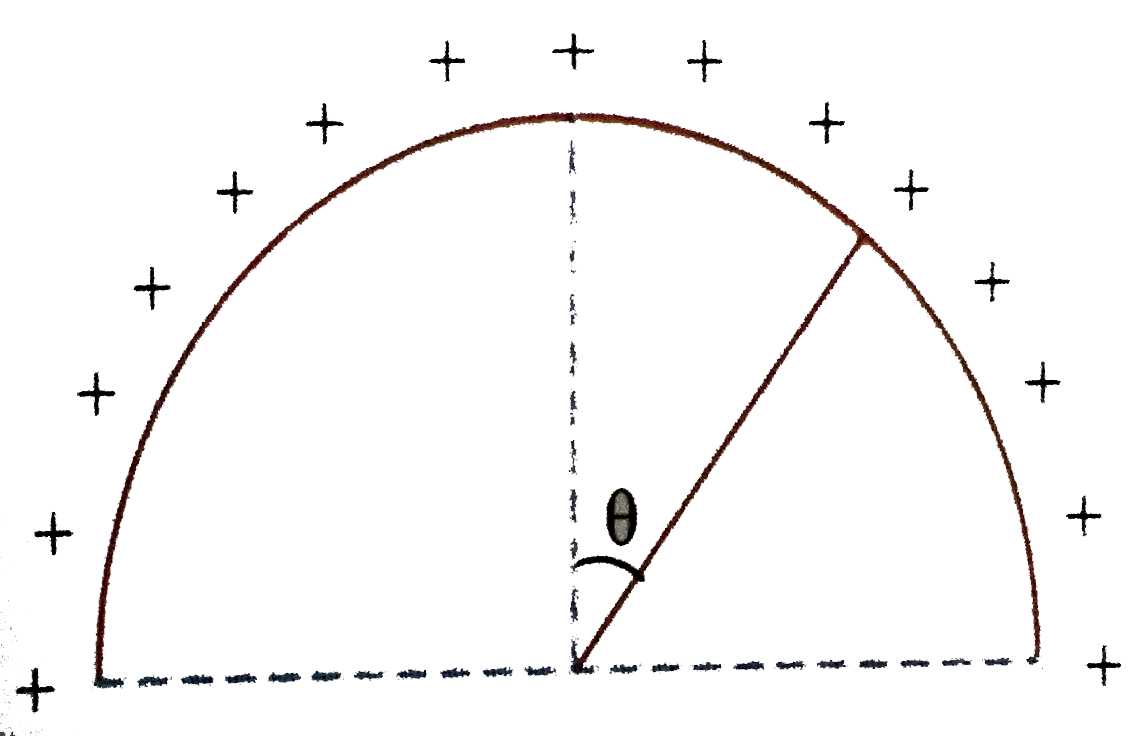 View Solution
View Solution

