The bisectors of ∠Band∠C of an isosceles triangle with AB=AC intersect each other at a point O.BO is produced to meet AC at a point M. Prove that ∠MOC=∠ABC.
Given Lines,OB and OC are the angle bisectors of ∠Band∠C of an isoceles ΔABC such that AB=AC which intersect each other at O and BO is produced to M.
To Prove
∠MOC=∠ABC
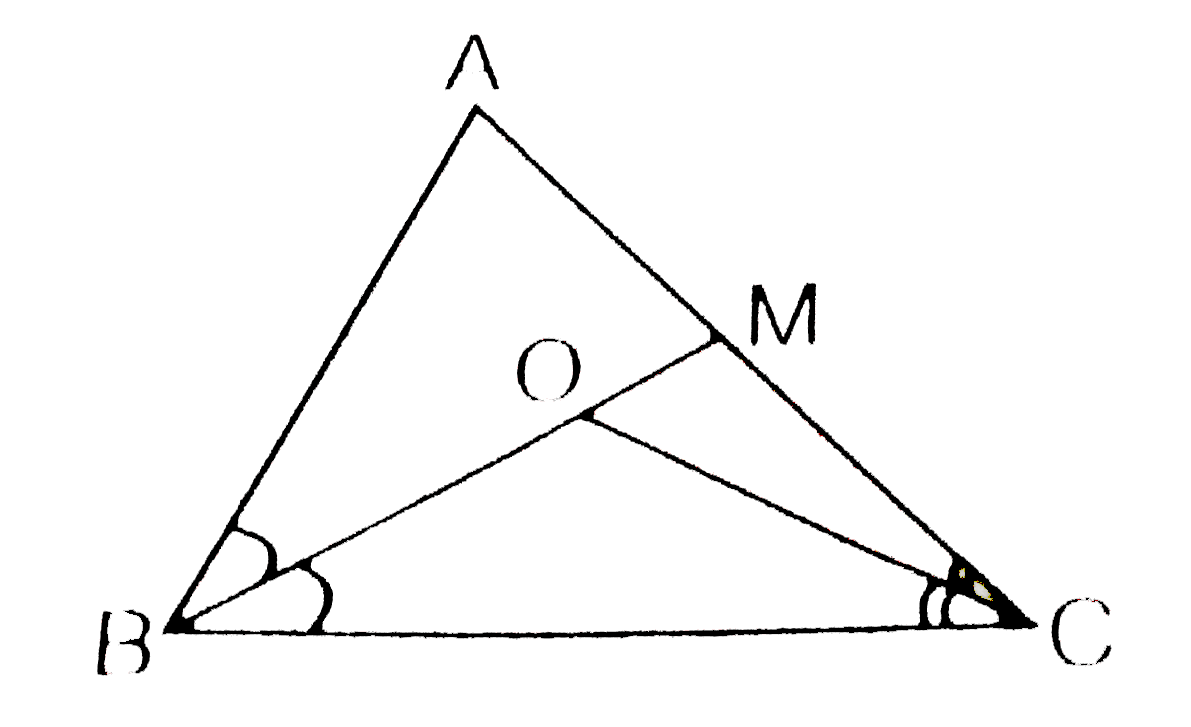
Proof In ΔABC AB=AC [given]
⇒ ∠ACB=∠ABC[angles opposite to equal sies are equal ]
12∠ACB=12∠ABC [dividing both sides by 2 ]
⇒ ∠OCB=∠OBC
[exterior angle of a triangle is equal to the sum of two interior of two interior angles ]
⇒ ∠MOC=∠OBC+∠OBC [from Eq.(i)]
⇒ ∠MOC=2∠OBC
⇒ ∠MOC=∠ABC [since,OB is the bisector of∠B]
Topper's Solved these Questions
Similar Questions
The bisectors of ∠Band∠C of an isosceles triangle with AB=AC intersect each other at a point O.BO is produced to meet AC at a point M. Prove that ∠MOC=∠ABC.
View SolutionBisector of the angles B and C of an isosceles triangle ABC with Ab = AC intersect each other at O. Shown that external angle agjacent to ∠ABC is equal to ∠BOC.
View SolutionThe bisectors of ∠Band∠C of an isosceles ΔABC with AB=AC intersect each other at point O. Show that the exterior angle adjacent to ∠ABC is equal to ∠BOC.
View SolutionThe bisector of ∠B of an isosceles triangle ABC with AB=AC meets the circumcircle of △ABC at P as shown in the figure. If AP and BC produced meet at Q prove that CQ=CA.
View SolutionBisectors of the angles B and C of an isosceles ΔABC with AB=AC intersect each other at 0.Show that external angle adejcent to ∠ABCis equato∠BOC.
View SolutionTriangle ABC is an isosceles triangle with AB=AC. Bisectors of ∠Band∠C intersect each other at O. join A−O and prove that
OB=OCView SolutionThe bisector of ∠B of an isosceles triangle ABC with AB=AC meets the circumcircle of ABC at P as shown in Figure. If AP and BC produced meet at Q,. prove that CQ=CA
View SolutionTriangle ABC is an isosceles triangle with AB=AC. Bisectors of ∠Band∠C intersect each other at O. join A−O and prove that
AO is bisector of ∠AView SolutionABC is an isosceles triangle with AB = AC. Draw AP⊥BC to show that ∠B=∠C.
 View Solution
View SolutionTriangle ABC is an isosceles triangle with AB=AC. Bisectors of ∠Band∠C intersect each other at O. join A−O and prove that
OB=OCView Solution

