Draw the graph of f(x)=sinx√1+tan2x−cosx√1+cot2x. Then find the range of f(x).
Text Solution
f(x)=sinx|secx|−cosx|cosec x|
=sinx⋅|cosx|−cosx⋅|sinx|
=⎧⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪⎩0,x∈(0, π/2)−sin2xx∈(π/2,π)0,x∈(π,3π/2)sin2x,x∈(3π/2,2π)
Clearly the domain of f(x) is R−{nπ2,n∈Z} and the period of f(x) is 2π.
So the range of f(x) is (-1, 1).
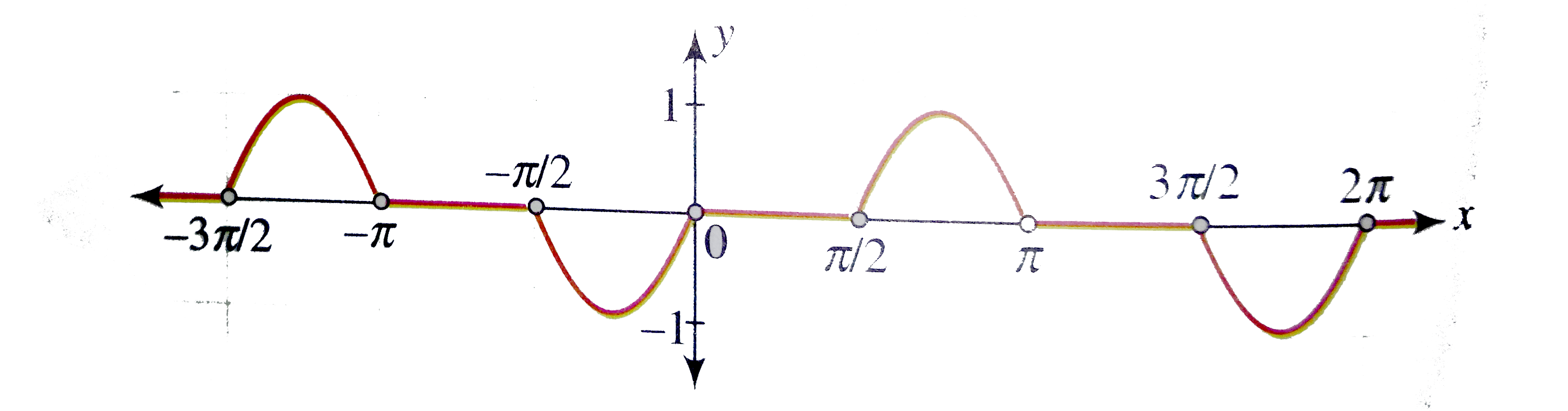
|
Topper's Solved these Questions
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise
34 Videos
- HIGHT AND DISTANCE BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year
3 Videos
Similar Questions
if:f(x)=sinx√1+tan2x−cosx√1+cot2x, then find the range of f(x)
View SolutionDraw the graph of f(x)=√sinx.
View SolutionDraw the graph of f(x)=√sinx.
View Solutionif:f(x)=sinx√1+tan2x−cosx√1+cot2x, then find the range of f(x)
View SolutionThe period off(x)=(sinx√1+tan2x)+(cosx√1+cot2x)is
View SolutionDraw the graph of f(x)=√1−e−x2
View SolutionDraw the graph of f(x)=√1−e−x2
View SolutionIf f:R→R,f(x)=√x2+1−3x√x2+1+x then find the range of f(x).
View SolutionIf f:R→R,f(x)=√x2+1−3x√x2+1+x then find the range of f(x).
View SolutionConsider the function defined by f(x)=sinx√1+tan2x+cosx√1+cot2x for permissible value. Then f(x)=0 (n is an integer) for
View Solution
