Question

The area of the region of the plane bounded by $max(\left|x\right|,\left|y\right|)\le 1andxy\le \frac{1}{2}$
is
$\frac{1}{2}+1n2sq\stackrel{.}{u}nits$
(b) $3+1n2sq\stackrel{.}{u}nits$

$\frac{31}{4}sq\stackrel{.}{u}nits$

(d) $1+21n2sq\stackrel{.}{u}nits$

Options

A. `1//2` + In 2 sq. units
B. 3+ In 2 sq. units
C. `31//4` sq. units
D. 1+2 In 2 sq. units

Answer

B

Explanation

`max (|x|,|y|)le1rArr |x| le 1 and |y| le 1`
which represent square bounded by `x=pm1 and y=pm1`

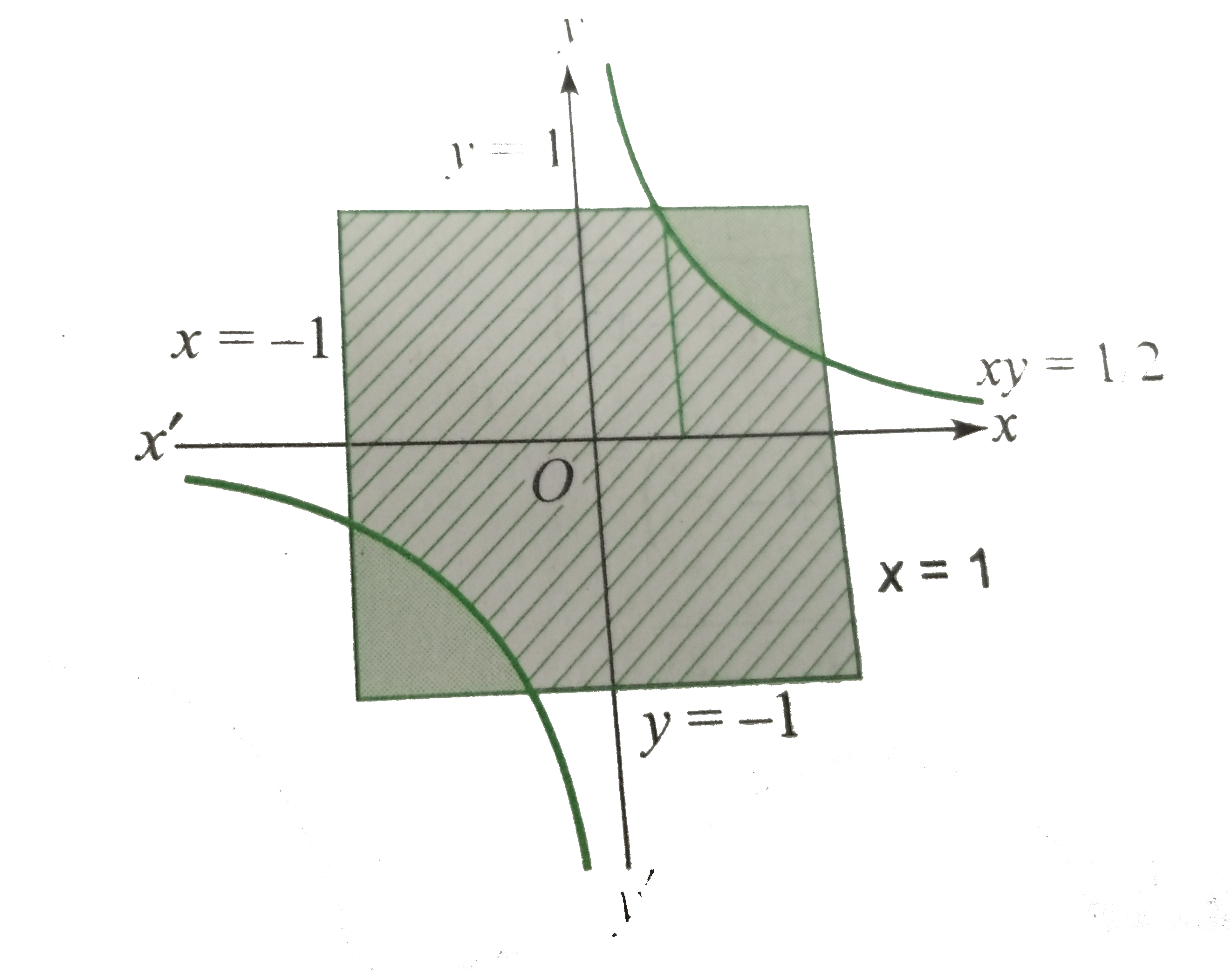
The required area is the lined area.
Now, shaded area is given by
`2overset(1)underset(1//2)int(1-(1)/(2x))dx=2(x-(1)/(2)" In "x)^(1)`
`=2[(1-0)-((1)/(2)-(1)/(2)" In "(1)/(2))]`
`=1-" In " 2` sq. units.
or Horizontal lined area `=4-(1-" In "2)=3+" In "2`. sq. units.