Question

Explain in detail Coulomb 's law and its various aspects.

Explanation

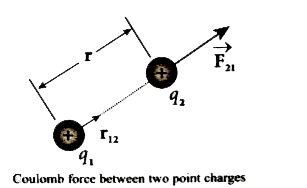
Consider two point charge `q_(1)` and `q_(2)` at rest in vacuum and separated by a distance of r . Accrording to Coulomb the force on the point charge `q_(2)` exerted by another point charge `q_(1)` is
`vecF_(21)= k (q_(1)q_(2))/(r_(2)) hatr_(12)`
where `hatr_(12)` is the unit vector directed from charge `q_(1)` to charge `q_(2)` and k is the proportionality constant .

Important aspects of Coulomb .s law :
(i) Coulomb.s law statres that the electrostatic force is directly proportional to the product of the magnitude of the two point charge and is inversely proportional to the square of the distance between the two point charges.
(ii) The force on the charge `q_(2)` exerted by the charge `q_(1)` always lies along the line joining the two charges `hatr_(21)` is the unit vector pointing from from charge `q_(1)` to `q_(2)` . Likewise the force on the charge `q_(1)` exerted by `q_(2)` is along -(i.e ., in the direction opposite to `hatr_(21))` .
(iii) In SI units k =`(1)/(4piepsilon_(0))` and its value is `9xx10^(9) Nm^(2)C^(-2)` . Here `epsilon_(0)` is the permittivity of free space or vacuum and the value of `epsilon_(0)=(1)/(4piepsilon_(0))= 8.85xx10^(-12)C^(2)N^(-1)m^(-2)`
(iv) The magnitude of the electrostatic force between two charges each of one coulomb and separated by a distance of 1 m is calculated as follows :
`[F]=(9xx10^(9)xx1xx1)/(1^(2))` . This is a huge quantity almost equivalent to the weight of one million ton. We never come across 1 coulomb of charge in practice. Most of the electrical phenomena in day - to -day life involve electrical charge of the order of `muC` ( micro coulomb ) or nC ( nano coulomb).
(v) In SI units Coulomb.s law in vacuum takes the form `vecF_(21) = (1)/(4piepsilon_(0))(q_(1)q_(2))/(r^(2))hatr_(12)` . In a medium of permittivity `epsilon`, the force between two point charges is given by `vecF_(21)=(1)/(4piepsilon_(0))(q_(1)q_(2))/(r_(2))hatr_(12)`.
(v) In SI units Coulomb .s law in vacuum takes the form `vec_(21)=(1)/(4piepsilon_(0))(q_(1)q_(2))/(r^(2))hat_(12)` . In a medium of permittivity `epsilon` the force between two point charge is given by `vecF_(21)= (1)/(4piepsilon_(0))(q_(1)q_(2))/(r^(2))hatr_(12)`.
Sin since `epsilon gt epsilon_(0)` the force between two point charge in a medium other than vacuum is always less than in vacuum. We define the relative permittivity for a given medium as `epsilon=(epsilon)/(epsilon_(0))` . For vacuum or air `epsilon_(r)=1` and for all other media `epsilon_(r) gt 1` .
(vi) Coulomb .s law has same structure as Newton.s law of gravitation . Both are inversely proportional to the square of the distance btween the particles . The electrostatic force ios directly proportional to the product of the magnitude of two point charges and gravitational force is directly proportional to the product of two masses.
(vii) The force on a charge `q_(1)` exerted by a point charge `q_(2)` is given by `vecF_(12)=(1)/(4piepsilon_(0))(q_(1)q_(2))/(r^(2))hatr_(21)`
Here `hatr_(21)` is the unit vector from charge `q_(2)` to `q_(1)` .
But `hatr_(21)= -hatr_(12), vecF_(12) =(1)/(4piepsilon_(0))(q_(1)q_(2))/(r^(2))(-hatr_(12))=-(1)/(4piepsilon_(0))(q_(1)q_(2))/(r^(2))(hatr_(12)` (or ) `vecF_(12)=-vecF_(21)`
Therefore the electrostatic force obeys Newton .s third law.
(viii) The expression for Coulomb force is true only for point charges. But the point charge is an ideal concept . However we can apply Coulomb.s law for two charged objects whose sizes are very much smaller than the distance between them . In fact Coulomb discovered his law by considering the charged spheres in the torsion balance as point charges . The distance between the two charge is much greater than the radii of the spheres.