Question

Discuss the various properties of conductors in electrostatic equilibrium . Properties of conductors in electrostatic equilibrium:

Explanation

(i) The electric field is zero everywhere inside the conducator . This is true regardless of whether the conductor ios solid or hollow . This is an experimental fact. Suppose the electric field is not zero inside the metal then there will be a force on the mobile charge carriers due to this electric field . As a result there will be a net motion of the mobile charges which contradicats the conductors being in electrostatic equilibrium. Thus the electric field is zero everywhere inside the conductor . we can also understand this fact by applying an external uniform electric field on the conductor.

Before applying teh external electric field the free electrons in the conductor are uniformly distributed in the conductor . When an electric field is applied the free electrons accelerate to the left causing the left plate to be negatively charged and the right plate to be positively charged . Due to this realignment of of free electrons there will be an internal electric field created inside the conductor which increases until it nullifies the external electric field . Once the external electric field is nullified the conductor is said to be in electrostatic equilibrium . The time taken by a conductor to reach electrostatic equilibrium is in the order of `10^(-16)` s, which can be taken as almost instantaneous.
(ii) There is no net charge inside the conductors . The charges must reside only on the surface of the conductors .
We can prove this property using Gauss law . Consider an arbitarily shaped conductor . A Gaussian surface is drawn inside the conductor such that it is very close to the surface of the conductor . Since the electric field is zero everywhere inside the conductor the net electric flux is also zero over this Gaussian surface . From Gauss.s law this implies that there is no net charge inside the conductor it immediately reaches the surface of the conductor .

(iii) The electric field outside the conductor is perpendicular to the surface of the conductor and has a magnitude of `(sigma)/(epsilon_(0))` where `sigma` is the surface charge density at that point .
If the electric field has components parallel to the surface of the conductor then free electrons on the surface of the conductor would experience acceleration . This means that the conductor is not in equilibrium . Therefore at electrostatic equilibrium the electric field must be perpendicular to the surface of the conductor.
We now prove that the electric field has magnitude `(sigma)/(epsilon_(0))` just outside the conductor .s surface . Consider a small cylindrical Gaussian surface . One half of this cylinder is embedded inside the conductor . Since electric field ios normal to the surface of the conductor the crurved part of the cylinder has zero . Hence the bottom flat part of the Gaussian surface has no electric flux . Therefore the top flat surface alone contributes to the electric flux. The electric field is parallel to the area vector and the total charge indside the surface is `sigma A`. By applying Gauss .s law `EA = (sigma A)/(epsilon_(0))`
In vector form `vecE = (sigma)/(epsilon_(0)) hatn`

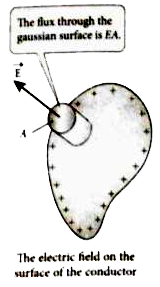
Here `hatn` represents the unit vector outward normal to the surface of the conductor . Suppose `sigma lt 0` then electric field poionts inward perpendicular to the surface.
(iv) The electrostatic potential has the same value on the surface and inside of the conductor .
We know that the conductor has no parallel electric component on the surface which means that charges can be moved on the suface withouth doing any work . This is possible only if the electrostatic potential is constant at all surface . Since the electric field is zero inside the conductor the potential is the same as the surface of the conductor . Thus at electrostatic equilibrium the conductor is always at equipotential.