Explain in detail the effect of a dielectric placed in a parallel plate capacitor. Solution in Tamil

Video Solution

Text Solution

Verified by Experts

(i) When the capacitor is disconnected from the battery: Consider a capacitor with two parallel plates each of cross - sectional area A and are separated by a distance d. The capacitor is charged by a battery of voltage $V_{0}$ and the charge stored is $Q_{0}$ . The capacitance of the capacitor without the dielectric is
$C_{0} = \frac{Q_{0}}{V_{0}}$
The battery is then disconnected from the capacitor and the dielectric is inserted between the plates . The introduction of dielectric between the plates will decrease the electric field . Experimentally it is found that the modifed electric field is given by
$E = \frac{E_{0}}{ε_{0}}$

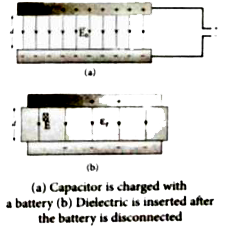
Here $E_{0}$ is the electric field inside the capacitors when there is no dielectric and $ε_{r}$ is the relative permeability of the dielectric or simply known as the dielectric constant . Since $ε_{r} > 1$ the electric field $E < E_{0}$ . As a result the electrostatic potential difference between the plates ( V - Ed) is also reduced . But at the same time the charge $Q_{0}$ will remain constant one the battery is disconnected. Hence the new potential difference is
$V = E d = \frac{E_{0}}{ε_{0}} d = \frac{V_{0}}{ε_{r}}$
We know that capacitance is inversely proportional to the potential difference . Therefore as V decreases C increases . Thus new capacitance in the presence of a dielectric is
$C = \frac{Q_{0}}{V} = ε_{0} \frac{Q_{0}}{V_{0}} = ε_{r} C_{0}$
Since $e_{r} > 1$ we have $C > C_{0}$ . Thus insertion of the dielectric $ε_{r}$ increases the capacitance . Using equation .
$C = \frac{ε_{0} A}{d}$
$C = \frac{ε_{r} ε_{0} A}{d} = \frac{ε A}{d}$
where $ε = ε_{r} ε_{0}$ is the permittivity of the dielectric medium . The energy stored in the capacitor before the insertion of a dielectric is given by
$U_{0} = \frac{1}{2} \frac{Q_{0}^{2}}{C_{0}}$
After the dielectric is inserted the charge $Q_{0}$ remains constant but the capacitance is increased . As a result the stored energy is decreased .
$U = \frac{1}{2} \frac{Q_{0}^{2}}{2 C} = \frac{1}{2} \frac{Q_{0}^{2}}{2 ε_{r} C_{0}} = \frac{U_{0}}{ε_{r}}$
Since $ε_{r} > 1$ we get $U < U_{0}$ . There is a decrease in energy because when the dielectric is inserted the capacitor spends some energy in pulling the dielectric inside .
(ii) When the battery remains connceted to the capacitor : Let us now condsider what happens when the battery of voltage $V_{0}$ remains connceted to the capacitor when the dielectric is inserted into the capacitor . The potential difference $V_{0}$ across the plates remains constant . But it is found experimentally ( first shown by Faraday ) that when dielectric is inserted the charge stored in the capacitor is increased by a fatcor $ε_{r}$ .
$Q = ε_{r} Q_{0}$
Due to this increased charge the capacitance is also increased . The new capacitance is
$C = \frac{Q}{V_{0}} = ε_{r} \frac{Q_{0}}{V_{0}} = ε_{r} C_{0}$

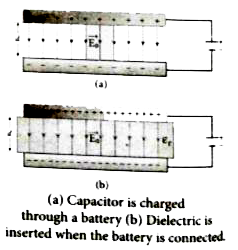
However the reason for the increase in capacitance in this case when the battery remains connected is diferent from the case when the battery is disconnected before introducing the dielectric .
Now $C_{0} = \frac{ε_{0} A}{d}$ and $C = \frac{ε_{0} A}{d}$
The energy stored in the capacitor before the insertion of a dielectric is given by
$U_{0} = \frac{1}{2} C_{0} V_{0}^{2}$
Note that here we have not used the expression
$U_{0} = \frac{1}{2} \frac{Q_{0}^{2}}{C_{0}}$
because here both charge and capacitance are changed whereas in equation 4 $V_{0}$ remains constant .
After the dielectric is inserted the capacitance is increased hence the stored energy is also increased .
$U = \frac{1}{2} C V_{0}^{2} = \frac{1}{2} ε_{r} C V_{0}^{2} = ε_{r} U_{0}$
Since $e_{r} > 1$ we have $U > U_{0}$
It may be noted here that since voltage between the capacitor $V_{0}$ is constant the electric field between the plates also remains constant .

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Similar Questions

FULL MARKS-ELECTROSTATICS -Textual Evaluation Solved ( III. Long Answer Questions: )

Home
Ask Doubt
Profile