Question

Derive the expression for resultant capacitance when capacitors are connected in series and in parallel .

Explanation

Capacitor in series and parallel:
(i) Capacitor in series : Consider three capacitors of capacitance `C_(1), C_(2)` and `C_(3)` connected in series with a battery of voltage V as shown in the figure (a). As soon as the battery is connected to the capacitor in series the electrons of charge -Q are transferred from negative terminal to the right plate of ` C_(3)` which pushes the electrons of same amount `(-Q)` from left plate of `C_(3)` to the right plate of `C_(2)` due to electrostatic induction. Similarly the left plate of `C_(2)` pushes the charges of `(-Q)` to the right plate of `C_(1)` which induces the positive charge `(+O)` on the left plate of `C_(1)` . At the same time electrons of charge `(-Q)` are transferred from left plate of `C_(1)` to positive terminal of the battery .

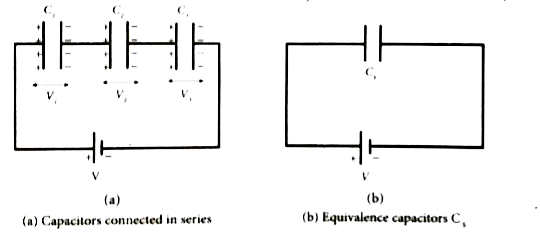
By these processes each capacitor stores the same amount of charge Q. The capacitances of the capacitors are in general different so that the voltage across each capacitor is also different and are denoted as `V_(1) , V_(2)` and `V_(3)` respectively .
The total voltage across each capacitor must be equal to the voltage of the a battery.
`V=V_(1) +V_(2) +V_(3)`
Since Q=CV we have `V= (Q)/(C_(1))+(Q)/(C_(2))+(Q)/(C_(3))`
`= Q((1)/(C_(1))+(1)/(C_(2))+(1)/(C_(3)))`
If three capacitors in series are considered to form an equivalent single capacitor `C_(5)`
shown in figure (b) then we have `V= (Q)/(C_(s))`
Substituting this expression into equation (2) we get
`(Q)/(C_(s))=Q((1)/(C_(1))+(1)/(C_(2))+(1)/(C_(3)))`
`(1)/(C_(s))=(1)/(C_(1))+(1)/(C_(2))+(1)/(C_(3))`
Thus the inverse of the equivalent capacitance `C_(s)` of three capacitors connected in series is equal to the sum of the inverses of each capacitance . This equivalent capacitance `C_(s)` is always less than the smallest individual capacitance in the series.
(ii) Capacitance in parallel : Consider three capacitors of capacitance `C_(1), C_(2) ` and `C_(3)` connected in parallel with a battery of voltage V as shown in figure (a)

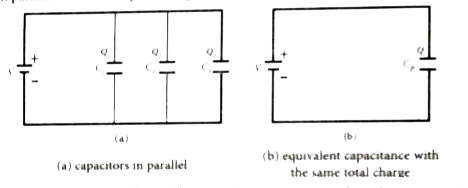
Since corresponding sides of the capacitors are connected to the same positive and negative terminals of the battery the voltage across each capacitor is equal to the battery.s voltage . Since capacitance of the capacitors is different the charge stored in each capacitor is not the same . Let the charge stored in the three capacitors be `Q_(1), Q_(3)` and `Q_(3)` respectively . According to the law of conservation of total charge the sum of these three charges is equal to the charge Q transferred by the battery,
`Q=Q_(1)+Q_(2)+Q_(3)`
Now since Q= CV we have
`Q=C_(1)V+C_(2)V+C_(3)V`
If these three capacitors are considered to form a single capacitance `C_(p)` which stores the total charge Q as shown in the figure (b) then we can write Q= CPV . Substituting this in equation (2) 2we get
`C_(p)V= C_(1)V+C_(2)V+C_(3)V`
Thus the equivalent capacitance of capacitors connected in parallel is equal to the sum of the individual capacitances . The equivalent capacitance `C_(p)` in a parallel connected is always greater than than the largest individual capacitance. In a parallel connection it is equivalent as area of each capacitance adds to give more effective area such that total capacitance increases.