Columns 1, 2 and 3 contain conics, equations of tangents to the conics and points of contact, respectively.

The tagent to a suitable conic (Column 1) at (√3,12) is found to be √3x+2y=4, then which of the following options is the only CORRECT combination?
(IV) (iv) (S)
(II) (iv) (R )
(IV) (iii) (S)
(II) (iii) (R )
The correct Answer is:b
Either option (b) or (c ) is correct.
Satisfying the point (√3,12) in (II), we get
a2=4.
∴ The conic is x2+4y2=4
Now, equation of tagent at (√3,12) is √3x+2y=4,
which is the given equation.
So, option (b) is correct.
Topper's Solved these Questions
- MISCELLANEOUSBOOK - IIT JEE PREVIOUS YEARCHAPTER - MISCELLANEOUSEXERCISE - MISCELLANEOUS
87 Videos
- MATRICES AND DETERMINANTSBOOK - IIT JEE PREVIOUS YEARCHAPTER - MATRICES AND DETERMINANTSEXERCISE - SOLVING SYSTEM OF EQUATIONS (INTEGER ANSWER TYPE QUESTION)
2 Videos
- PARABOLABOOK - IIT JEE PREVIOUS YEARCHAPTER - PARABOLAEXERCISE - TOPIC 4 DIAMETER, CHORD OF CONTACT, CHORD BISECTED AND PRODUCT OF PAIR OF TANGENTS OBJECTIVES QUESTION II (ANALYTICAL & DESCRIPTIVE )
5 Videos
Similar Questions
Matching the information given in the three columns of the following table column 1, 2 and 3 contain conics, equations of tangents in the conics and points of contact, respectively.
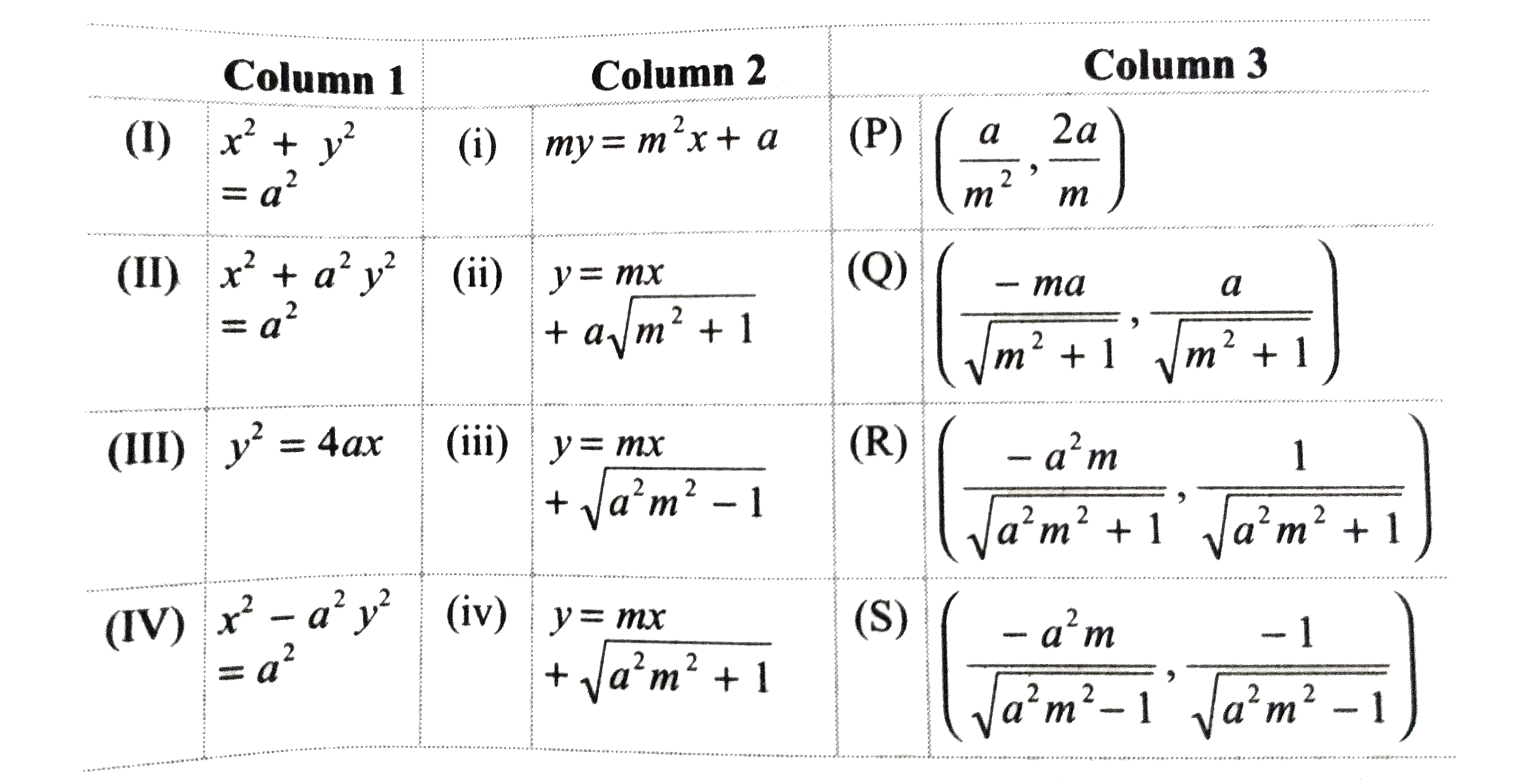
Q. The tangent to a suitable conic (column 1) at (√3,12) is found to be √3x+2y=4, then which of the following options is the correct combination?
View SolutionMatching the information given in the three columns of the following table column 1, 2 and 3 contain conics, equations of tangents in the conics and points of contact, respectively.
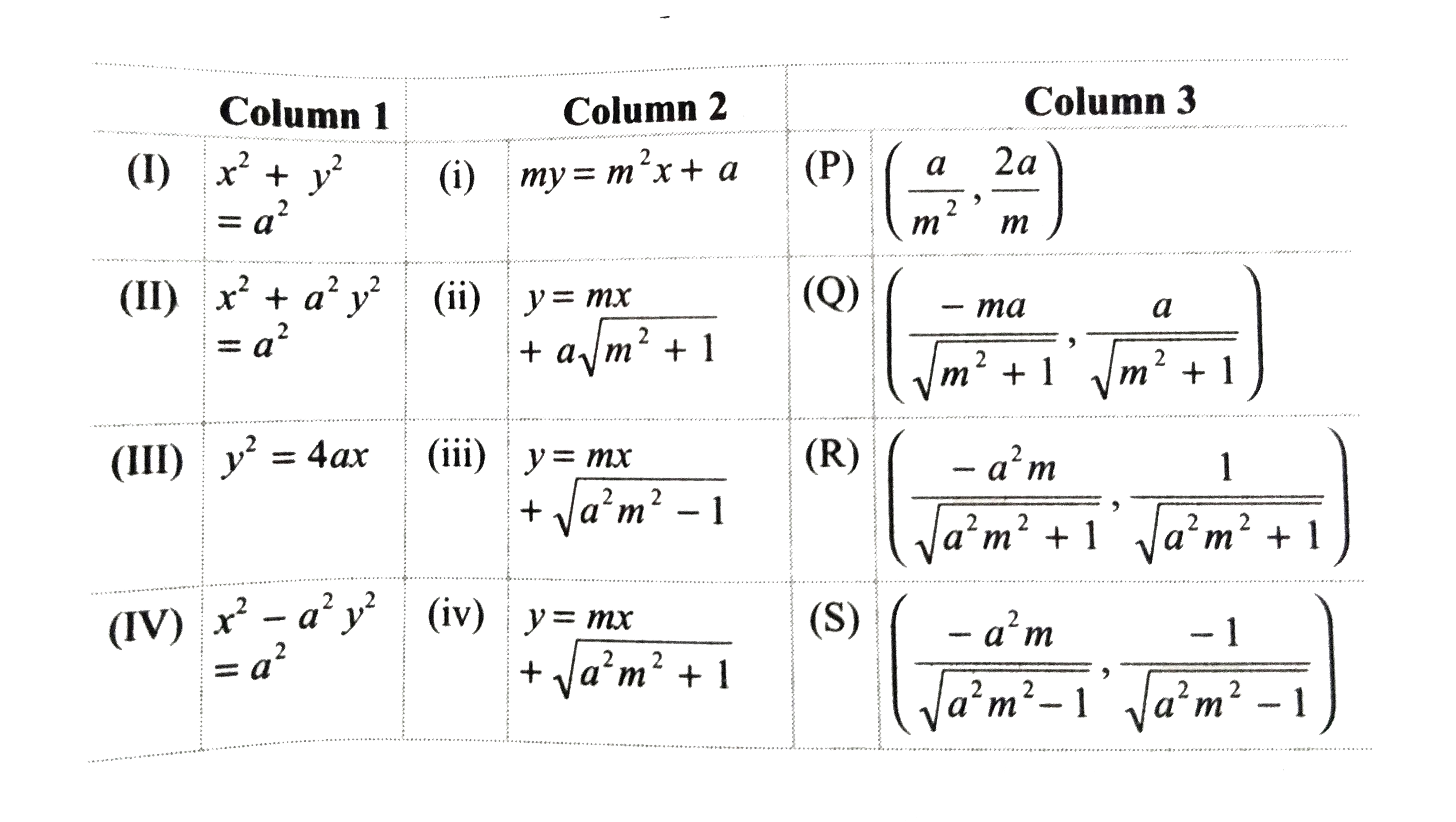
Q. For a=√2), if a tangent is drawn to a suitable conic (Column 1) at the points of contact (-1, 1), then which of the following options is the only correct combination for obtaining its equation?
View Solution
Knowledge Check
Lists I, II and III contains conics, equation of tangents to the conics and points of contact, respectively.

If the tangent to a suitable conic (List I) at (√312) is found to be √3x+2y=4. then which of the following options is the only CORRECT combination?A(II) (iii) (R)B(IV) (iv) (S)C(IV) (iii) (S)D(II) (iv) (R)Lists I, II and III contains conics, equation of tangents to the conics and points of contact, respectively.

If a tangent to a suitable conic (List I) is fond to be y = x+8 and its point of contact is (8, 16), then which of the following options I sthe only CORRECT combination?A(II) (i) (P)B(III) (i0) (Q)C(II) (iv) (R)D(I) (ii) (Q)Lists I, II and III contains conics, equation of tangents to the conics and points of contact, respectively.

For a=√2 if a tangent is drawn to a suitable conic (List I) at the point of contact (−1,1), which of the following options is the only CORRECT combination for obtaining its equation?A(II) (ii) (Q)B(III) (i) (P)C(I) (i) (P)D(I) (ii) (Q)
Column 1,2 and 3 contains conics, equations of tangents to the conics and points of contact, respectively. Column I, Column 2, Column 3 I, x2+y2=a , (i), my=m2x+a , (P), (am2,2am) II, x2+a2y2=a , (ii), y=mx+a√m2+1 , (Q), (−ma√m2+1,a√m2+1) III, y2=4ax , (iii), y=mx+√a2m2−1 , (R), (−a2m√a2m2+1,1√a2m2+1) IV, x2−a2y2=a2 , (iv), y=mx+√a2m2+1 , (S), (−a2m√a2m2+1,−1√a2m2+1) The tangent to a suitable conic (Column 1) at (√3,12) is found to be √3x+2y=4, then which of the following options is the only CORRECT combination? (IV) (iii) (S) (b) (II) (iii) (R) (II) (iv) (R) (d) (IV) (iv) (S)
View SolutionFind the equation of tangent to the conic x2−y2−8x+2y+11=0 at (2,1)
View SolutionFind the equation of tangent to the conic x2−y2−8x+2y+11=0 at (2,1).
View SolutionFind the equation of tangent to the conic x2−y2−8x+2y+11=0 at (2,1)
View SolutionColumn 1,2 and 3 contains conics, equations of tangents to the conics and points of contact, respectively. Column I, Column 2, Column 3 I, x2+y2=a , (i), my=m2x+a , (P), (am2,2am) II, x2+a2y2=a , (ii), y=mx+a√m2+1 , (Q), (−ma√m2+1,a√m2+1) III, y2=4ax , (iii), y=mx+√a2m2−1 , (R), (−a2m√a2m2+1,1√a2m2+1) IV, x2−a2y2=a2 , (iv), y=mx+√a2m2+1 , (S), (−a2m√a2m2+1,−1√a2m2+1) For a=√2,if a tangent is drawn to a suitable conic (Column 1) at the point of contact (−1,1), then which of the following options is the only CORRECT combination for obtaining its equation? (I) (ii) (Q) (b) (III) (i) (P) (II) (ii) (Q) (d) (I)(i)(P)
View Solution
