Match the statements given in Column I with the values given in Column II.
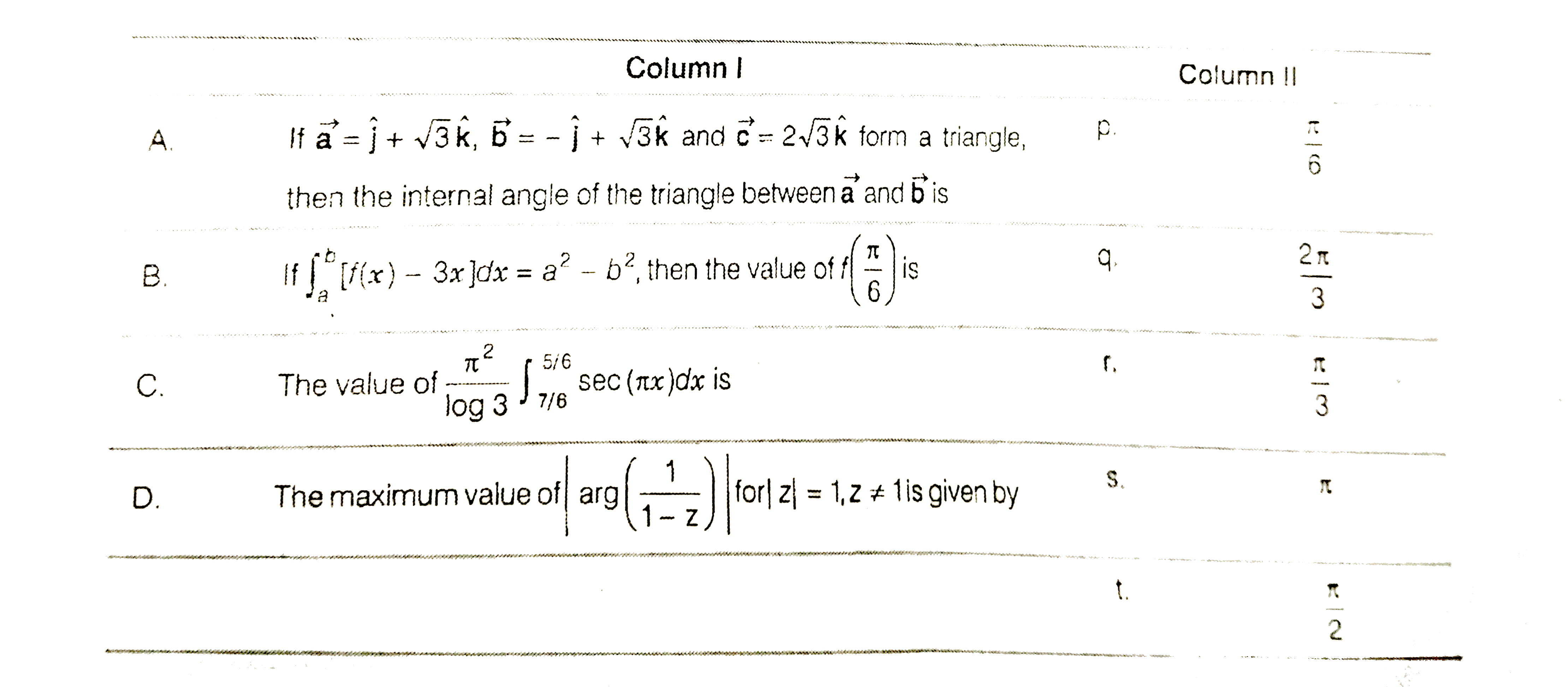
The correct Answer is:A→q;B→p;C→s;D→s
(A) |→a|=√1+3=2
∣∣→b∣∣=√1+3=2,|→c|=√12=2√3
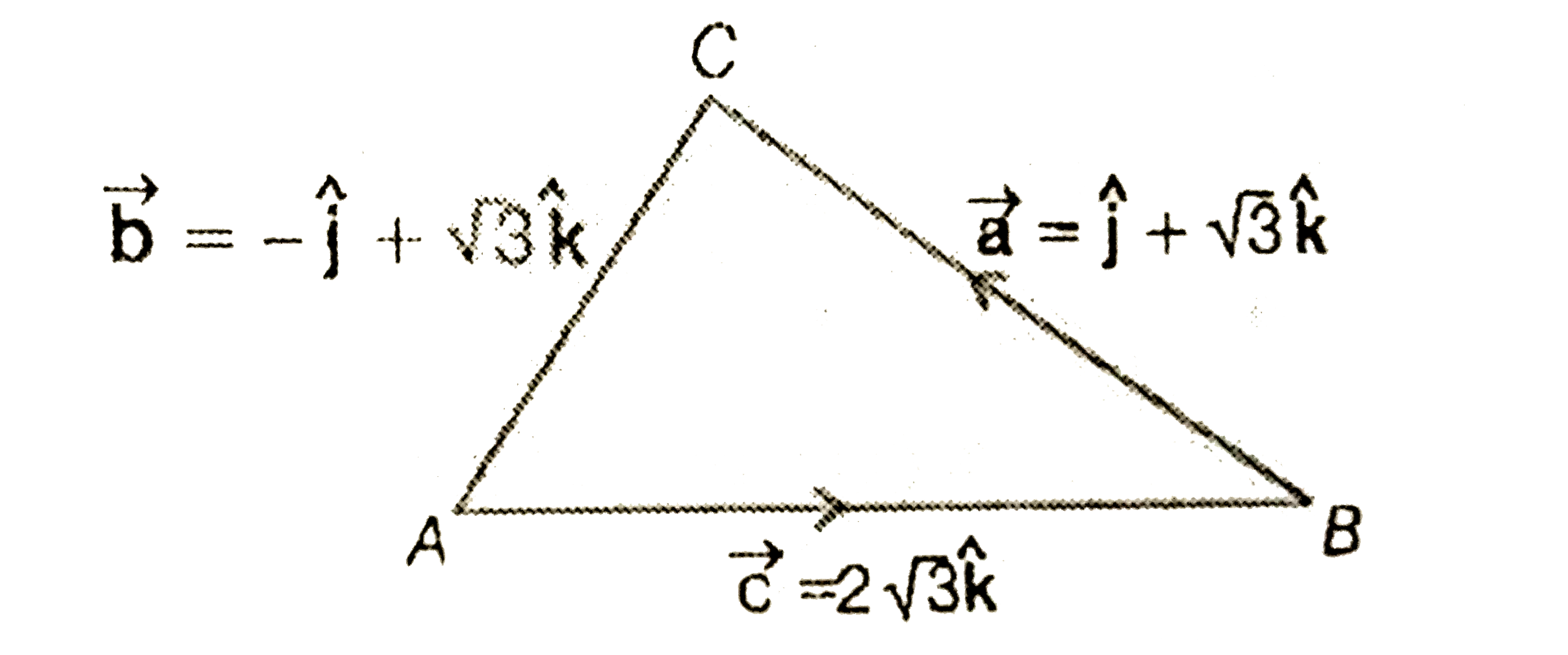
Using cosine law,
cosC=|→a|2+∣∣→b∣∣2−|→c|22|→a|∣∣→b∣∣=4+4−122×2×2=−48=−12
⇒∠C=120∘=2π3
(B) ∫baf(x)dx−3(x22)ba=(a2−b2)
⇒∫baf(x)dx−32(b2−a2)=(a2−b2)
⇒∫baf(x)dx=(a2−b2)+32(b2−a2)=b2−a22
⇒∫baf(x)dx=b2−a22
∴f(x)=x⇒f(π6)=π6
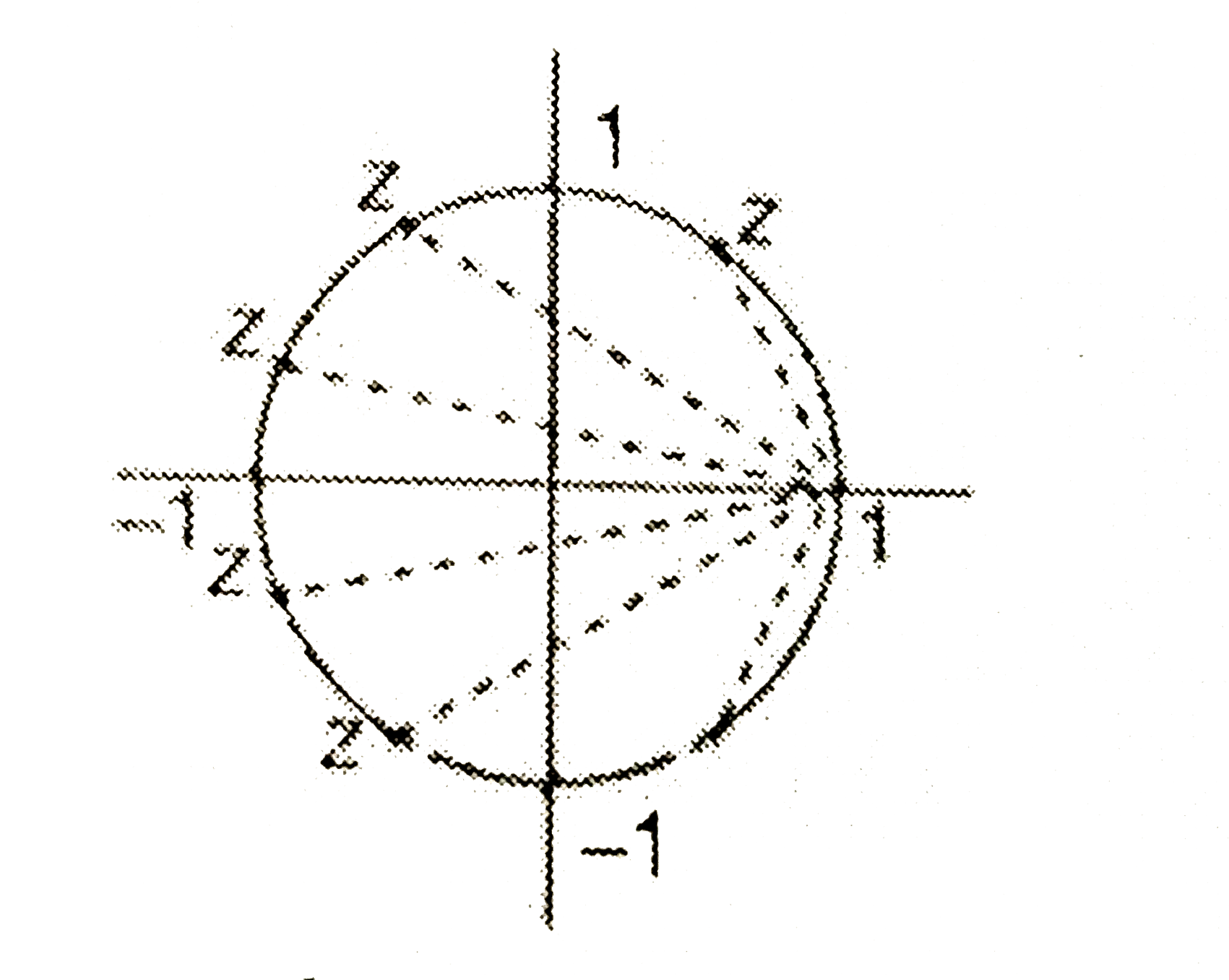
(C) π2loge3∫5/67/6sec(πx)dx
⇒π2loge3{loge|secπx+tanπx|π}5/67/6
⇒πloge3{loge∣∣∣sec5π6+tan5π6∣∣∣−loge∣∣∣sec7π6+tan7π6∣∣∣}
⇒πloge3{loge∣∣√3∣∣−loge∣∣∣1√3∣∣∣}
⇒πloge3{loge3}=π
(D) ∣∣∣arg11−z∣∣∣ for |z|=1⇒∣∣arg(1−z)−1∣∣
⇒|−arg(1−z)|
⇒|arg(1−z)|
From figure, arg (z - 1) is maximum ⇒π
Topper's Solved these Questions
- MISCELLANEOUSBOOK - IIT JEE PREVIOUS YEARCHAPTER - MISCELLANEOUSEXERCISE - MISCELLANEOUS
87 Videos
- MATRICES AND DETERMINANTSBOOK - IIT JEE PREVIOUS YEARCHAPTER - MATRICES AND DETERMINANTSEXERCISE - SOLVING SYSTEM OF EQUATIONS (INTEGER ANSWER TYPE QUESTION)
2 Videos
- PARABOLABOOK - IIT JEE PREVIOUS YEARCHAPTER - PARABOLAEXERCISE - TOPIC 4 DIAMETER, CHORD OF CONTACT, CHORD BISECTED AND PRODUCT OF PAIR OF TANGENTS OBJECTIVES QUESTION II (ANALYTICAL & DESCRIPTIVE )
5 Videos
Similar Questions
Match the detergents given in Column I with their uses given in Column II.
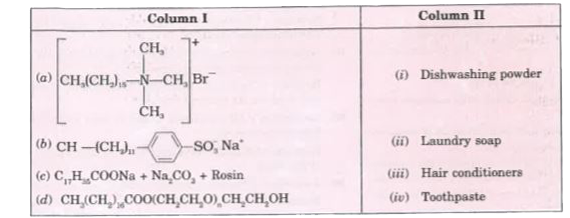
View SolutionMatch the statement given in Column I with the phenomenon given in Column II.

View SolutionMatch the statement given in Column I with the phenomenon given in Column II.

View SolutionMatch the terms given in Column I with the statements given in Column II

View SolutionMatch the reactions given in Column I with the names given in Column II.
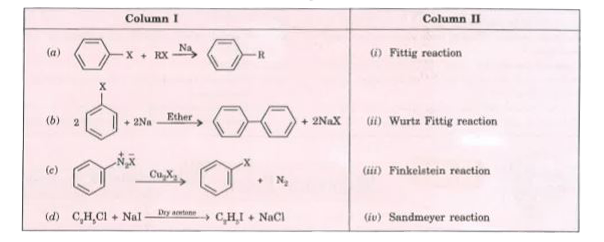
View SolutionMatch the statements given in column-I with statements given in column-II

View SolutionMatch the statement given in Column I. with the phenomenon given in column II.
View SolutionMatch the terms given in Column I with the compounds given in Column II.

View SolutionMatch the mediccne given in Column I with their use given in Column II .

View SolutionMatch the terms given in Column I with the units given in Column II.

View Solution
