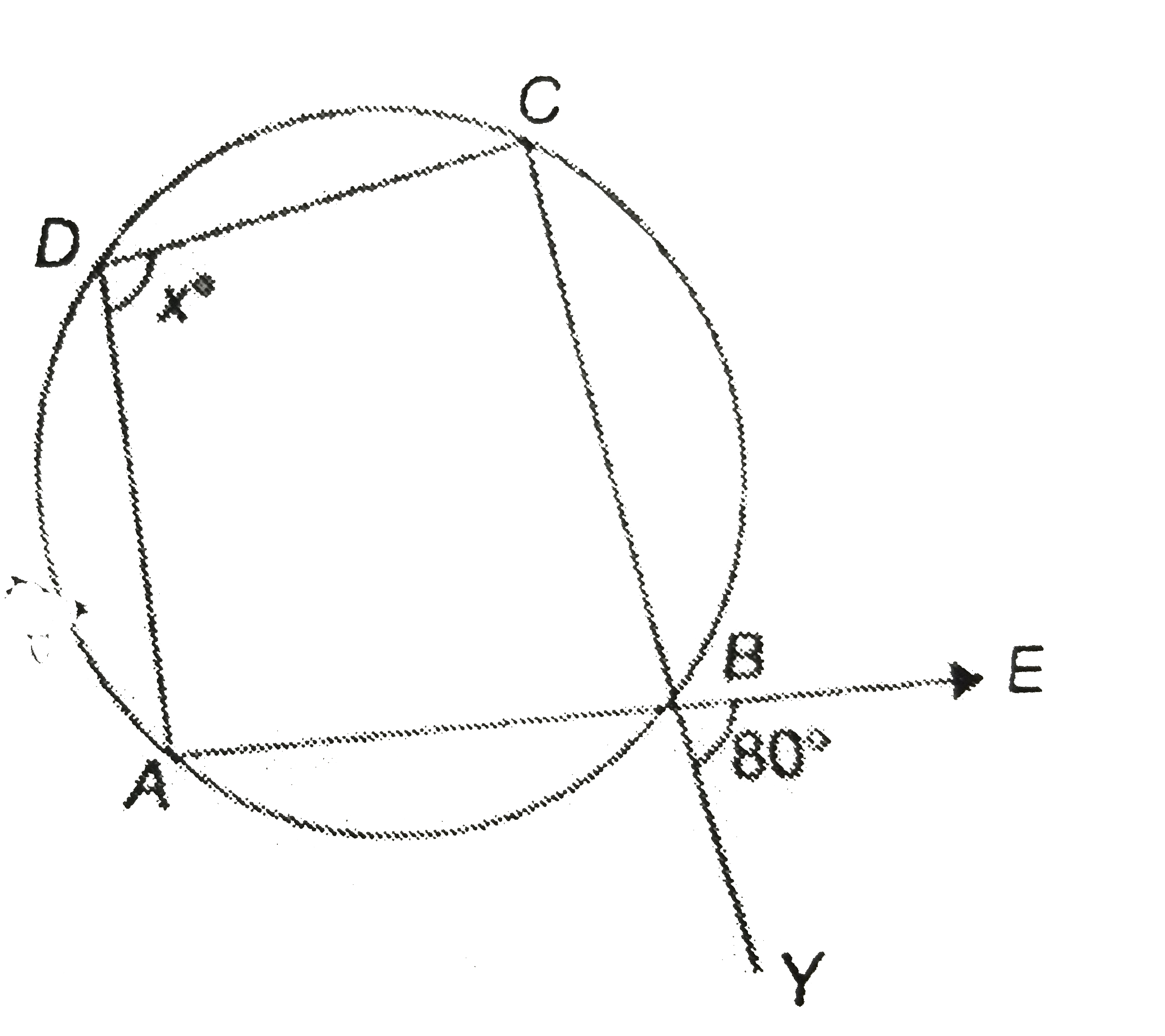
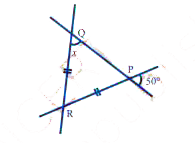
In Fig, find the value of x.
Video Solution
Text Solution
The correct Answer is:A→p,q,r,s;B→p,t;C→p,q,r,t;D→s
A→P,Q,B→P,Q,C→P,Q,S,T,D→Q,T
A. Projection of (αˆi+βˆj)on(√3ˆj+ˆj)=√3
⇒∣∣∣√3α+β2∣∣∣=√3
⇒√3α+β=±2√3 ...(i)
andα−√3β=2 ...(ii)
On solving Eqs. (i) and (ii), we get
α=2,−1
∴|α|=2,1
B. Since, if any function is differentiable, then it is continuous for all x.
By continuity at x=1,
−3a−2=b+a2 ...(i)
By differentiability, f'(x)={−6ax,x<1b,x>1
∴−6a=b ...(ii)
From Eqs. (i) and (ii), we get
−3a−2=−6a+a2
⇒a2=3a+2=0→a=1,2
C. (3−3w+3w2)4n+3+(2+3w−3w2)4n+3=(−3+2w+3w2)4n+3=0
⇒{(−3+2w+3w2)w}4n+3+{(−3+2w+3w2)w2}4n+3+{(−3+2w+3w2)}4n+3=0
⇒(−3+2w+3w2)4n+3{w4n+3+(w2)4n+3+1}=0
⇒wn+w2n+1=0
which is true only when n is not a multiple of 3.
∴n=1,2,4,5
D. Here, 2aba+b=4and2(5−a)=b−5
⇒b=15−2a ...(i)
Now, 2ab=4(a+b)
⇒2a(15−2a)=4(a+15−2a)
⇒15a−2a2=30−2a
⇒2a2−17a+30=0
⇒a=5/2,6
Hence, |q−2a|=|10−2a|=5or2
|
Topper's Solved these Questions
- MISCELLANEOUSBOOK - IIT JEE PREVIOUS YEARCHAPTER - MISCELLANEOUSEXERCISE - MISCELLANEOUS
87 Videos
- MATRICES AND DETERMINANTSBOOK - IIT JEE PREVIOUS YEARCHAPTER - MATRICES AND DETERMINANTSEXERCISE - SOLVING SYSTEM OF EQUATIONS (INTEGER ANSWER TYPE QUESTION)
2 Videos
- PARABOLABOOK - IIT JEE PREVIOUS YEARCHAPTER - PARABOLAEXERCISE - TOPIC 4 DIAMETER, CHORD OF CONTACT, CHORD BISECTED AND PRODUCT OF PAIR OF TANGENTS OBJECTIVES QUESTION II (ANALYTICAL & DESCRIPTIVE )
5 Videos
Similar Questions
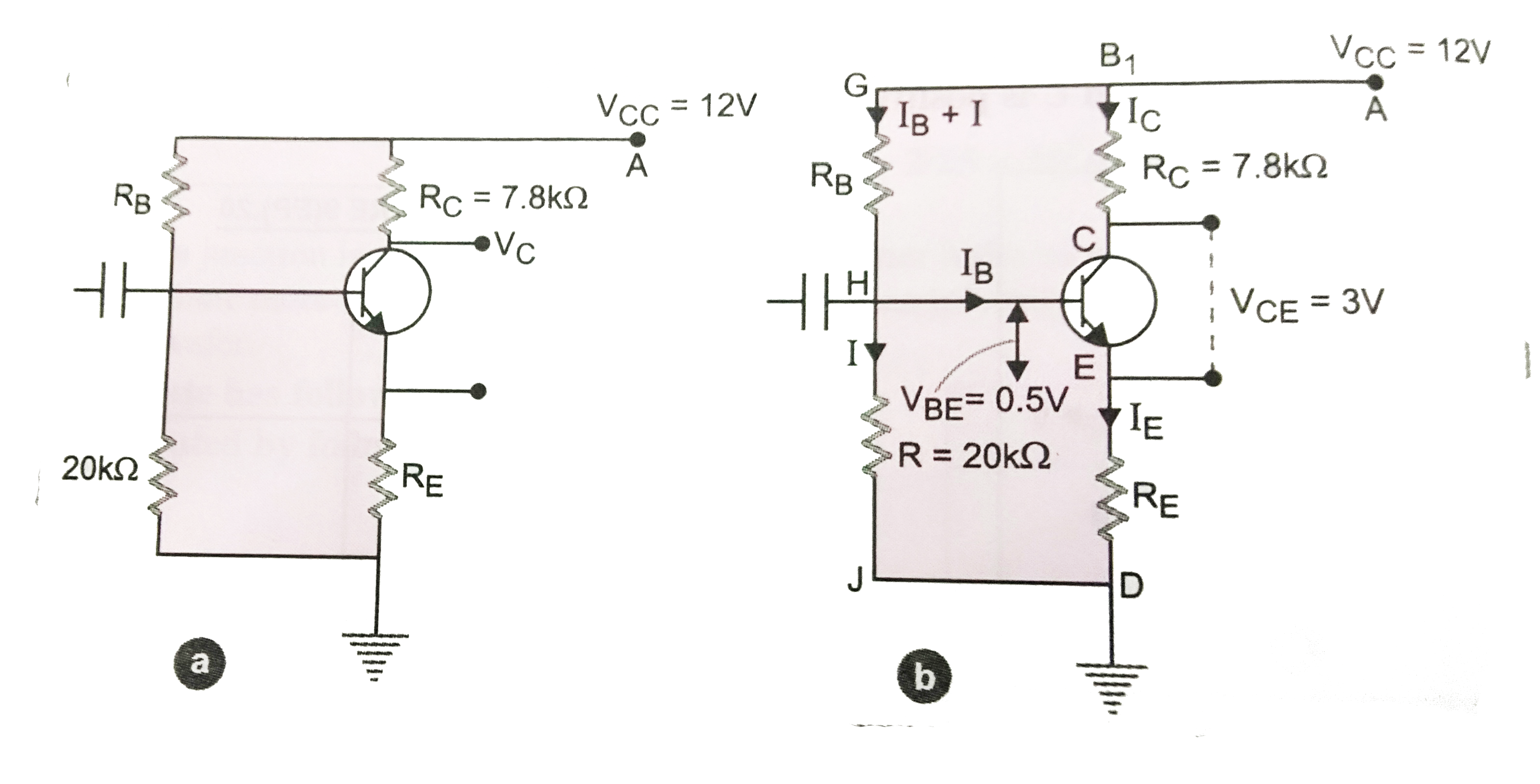
In the circuit shown in Fig., find the value of R.
View SolutionIn Fig.32, find the values of x,y and z.
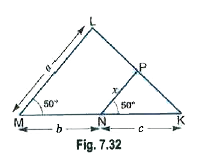
View SolutionIn the given Fig. 7.32, find the value of x in terms of a, b and c.
View SolutionIn Fig. 6.40, find the values of x, y and z.

View SolutionIn Fig. 6.28, find the values of x and y and then show that AB || CD.

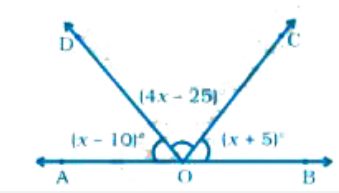
View SolutionIn Fig. 5.53, find the value of BOC, if points A, O and B are collinear.
View SolutionIn Fig. 4.71, if ABCD , find the value of x . (FIGURE)
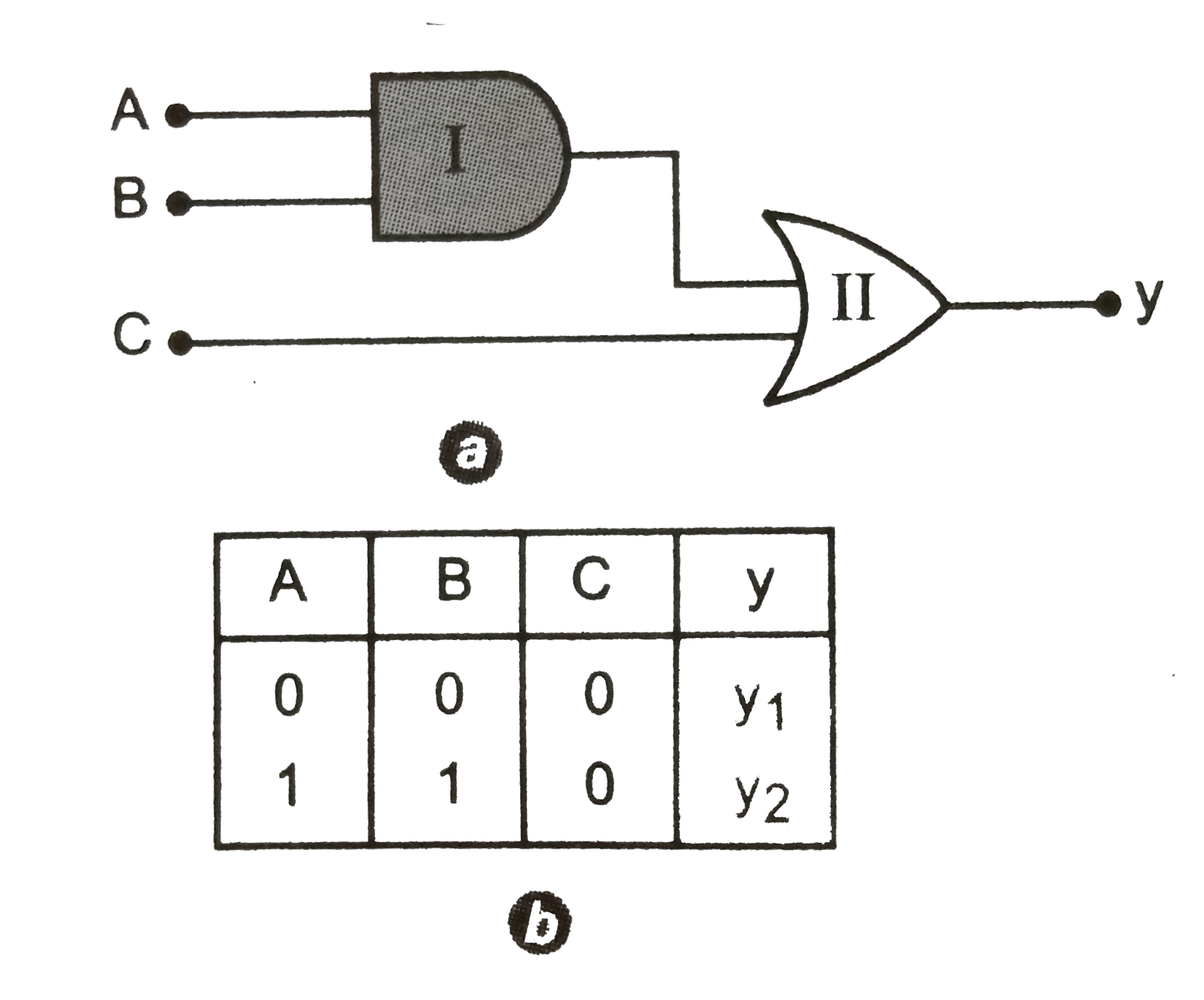
View SolutionFor the given combination of gates shown in Fig., find the values of output y1 and y2 in the table given below Fig. Identify the gates I and II.
View SolutionIn Fig.73, the value of x is 20 (b) 30 40 (d) 25
View SolutionIn Fig. 6.44, if RP = RQ, find the value of x.
View Solution
