Match the statements given in Column I with the values given in Column II.

The correct Answer is:A→t,B→pandr,C→q,D→r
(A) Equation of the line passing through origin is
xa=yb=zc
∴∣∣
∣∣21−11−21abc∣∣
∣∣=0
⇒a(−1)−b(3)+c(−5)=0
⇒−a−3b−5c=0
⇒a+3b+5c=0 ...(i)
Also, ∣∣
∣
∣∣83−312−11abc∣∣
∣
∣∣=0
∴a(−2)−b(23)+c(103)=0
⇒2a+2b3−10c3=0
⇒3a+b−5c=0 ...(ii)
From Eqs. (i) and (ii), a−20=b20=c−8
a5=b−5=c4
Equation of line is
x5=y−5=z4=λ [say]...(ii)
Also x−21=y−1−2=z+11=k1 [say]...(iv)
Now, x−832=y+3−1=z−11=k2 [say]...(v)
Point on Eq. (iii) is (5λ,−5λ,+4λ).
Point on Eq. (iv) is (2+k1,1−2k1,−1+k1).
Point on Eq. (v) is (83+2k2,−3−k2,1+k2).
On solving , 2+k1+1−2k1=0⇒−k1+3=0
⇒k1=3
P≡(5,−5,2)
Again, for Q,83+2k2−3−k2=0
⇒k2−13=0
⇒k2=1/3
∴Q=(103,−103,43)
Now, PQ=√(53)2+(53)2+(23)2=√543
⇒PQ2=d2=549=6
(B) tan−1(x+3−x+31+(x2−9))=tan−1(34)⇒6x2−8=34
⇒3x2=48
⇒x=±4
( C) (→b−→a)⋅(→b+→a−μ→b4)=0
⇒(→b−→a)⋅(4→b+→a−μ→b)=0
(4−μ)→b2−→a2=0 ...(i)
Also, 2∣∣
∣∣→b+→a−μ→b4∣∣
∣∣=∣∣→b−→a∣∣
⇒2∣∣
∣∣(4−μ)→b+→a4∣∣
∣∣=∣∣→b−→a∣∣
⇒(4−μ)2→b24+→a24=→b2+→a2
⇒3→a24=(4−μ)2−44⋅→b2⇒3→a2=→b2(4−μ)2−4→b2 ...(ii)
From Eqs. (i) and (ii) ,
3(4−μ)=(4−μ)2−4
(4−μ)2−3(4−μ)−4=0⇒μ=0,5
μ=5 is not admissible .
(D) f(0)=9,f(x)=sin(9x2)sinx2=(3−4sin2x2)(3−4sin23x2)
=9−12sin2x2−12sin23x2+16sin2x2⋅sin23x2
=9−6(1−cosx)−6(1−cos3x)+4(1−cosx)(1−cos3x)
=1+6cosx+6cos3x−4cosx−4cos3x+4cosxcos3x
Let I=2π∫π−πsin9x2sinx2dx=4π∫π01+2cosx+2cos3x+2(cos4x+cosx)dx=4π×π=4
Topper's Solved these Questions
- MISCELLANEOUSBOOK - IIT JEE PREVIOUS YEARCHAPTER - MISCELLANEOUSEXERCISE - MISCELLANEOUS
87 Videos
- MATRICES AND DETERMINANTSBOOK - IIT JEE PREVIOUS YEARCHAPTER - MATRICES AND DETERMINANTSEXERCISE - SOLVING SYSTEM OF EQUATIONS (INTEGER ANSWER TYPE QUESTION)
2 Videos
- PARABOLABOOK - IIT JEE PREVIOUS YEARCHAPTER - PARABOLAEXERCISE - TOPIC 4 DIAMETER, CHORD OF CONTACT, CHORD BISECTED AND PRODUCT OF PAIR OF TANGENTS OBJECTIVES QUESTION II (ANALYTICAL & DESCRIPTIVE )
5 Videos
Similar Questions
Match the terms given in Column I with the statements given in Column II

View SolutionMatch the statement given in Column I with the phenomenon given in Column II.

View SolutionMatch the statement given in Column I with the phenomenon given in Column II.

View SolutionMatch the reactions given in Column I with the names given in Column II.
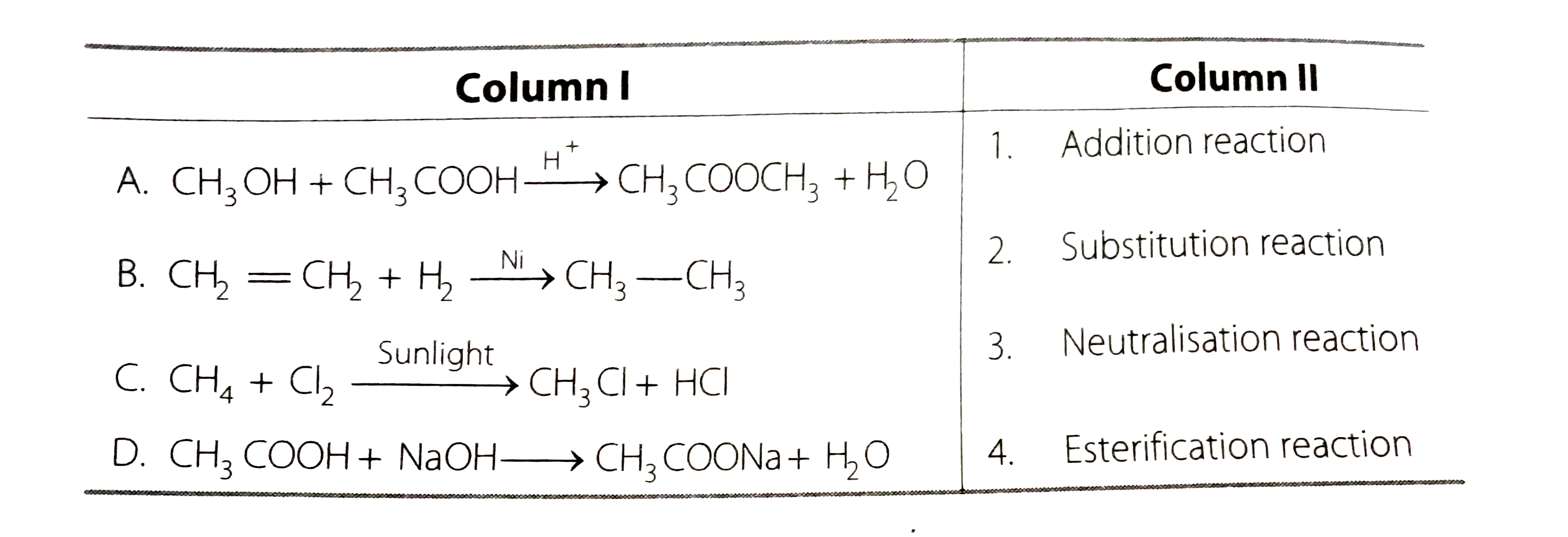
View SolutionMatch the statements given in column-I with statements given in column-II

View SolutionMatch the statement given in Column I. with the phenomenon given in column II.
View SolutionMatch the statements/expressions given in Column I with the values given in Column II.

View SolutionMatch the statements/expressions given in Column I with the values given in Column II.

View SolutionMatch the statements/expressions given in Column I with the values given in Column II.

View SolutionMatch the statements/expressions given in Column I with the values given in Column II. '

View Solution
