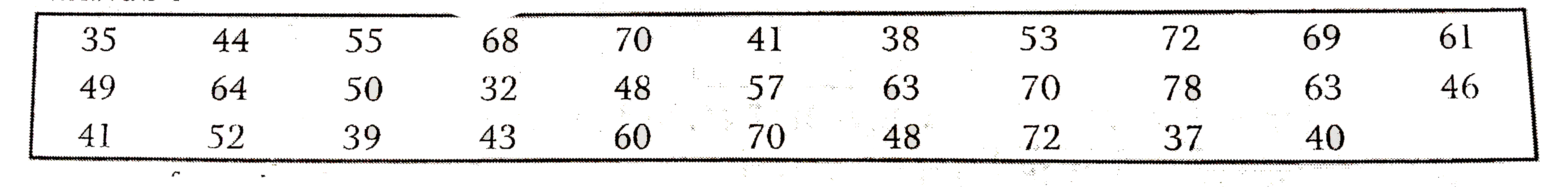The marks obtained by 40 students are grouped in a frequency table in class intervals of 10 marks each. The mean and the variance obtained from this distribution are found to be 40 and 49, respectively. It was later discovered that two observations belonging to the class interval (21 - 30) were included in the class interval (31 - 40) by mistake. Find the mean and the variance after correcting the error.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:49.25

Given , n=40,¯x=40,var(x)=49
⇒¯x=Σfixi40=40⇒Σfixi=1600
Also, var(x)=49
⇒140Σfi(xi−40)2=49
∴49=140(Σx2ifi)−2Σxifi+40Σfi
⇒49=140(Σx2ifi)−2(1600)+40×40
∴Σx2ifi=1649×40
Let (21-30) and (31-40) denote the kth and (k + 1)th class intervals, respectively.
Then, if before correction fkandfk+1 are frequencies of those intervals, then after correction (2 observations are shifted form (31-40) to (21-30), frequency of kth interval becomes fk+2 and frequency of (k+1)th interval becomes fk+1−2
∴¯xnew=140⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩40∑i=1fixii≠k,k+1+(fk+2)xk+(fk+1−2)xk+1⎫⎪ ⎪ ⎪⎬⎪ ⎪ ⎪⎭
¯xnew=140{40∑i=1fixi}+240{(xk−xk+1)}
=14040∑i=1fixi+120(−10)=39.5
=140[40∑i=1fi(xi−39.5)2+fk(xk−39.5)2+fk+1(xk+1−39.5)2 where i≠k,k+1]
=140[Σ(fix2i−79fixi+(39.5)2fi)]
=14040∑i=1fi⋅x2i−79(140)40∑i=1fixi+(39.5)2⋅14040∑i=1fi
=1649−3160+1560.25=49.25

Updated on:21/07/2023
|
Class 12MATHSQUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The table shows the marks obtained by 25 students in a class test. Find the mean of the marks obtained
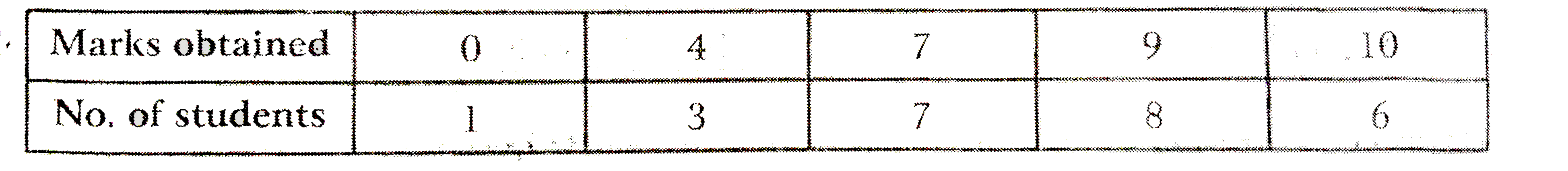    ocr_image

    A7.72
    B7.65
    C7.4
    D7

  • The mean and SD of the marks of 200 candidates were found to be 40 and 15, respectively. Later, it was discovered that a score 40 was wrongly read as 50. The correct mean and SD are respectively

    A14.98,39.95
    B39.95,14.98
    C39.95,224.5
    DNone of these

  • Class mark of class interval 60–70 is

    A60
    B70
    C65
    D72