Match List I with List II and select the correct answer using the codes given below the lists :

A

$\begin{matrix} P & Q & R & S (iv) & (iii) & (ii) & (i) \end{matrix}$

B

$\begin{matrix} P & Q & R & S (ii) & (iv) & (iii) & (i) \end{matrix}$

C

$\begin{matrix} P & Q & R & S (iv) & (iii) & (i) & (ii) \end{matrix}$

D

$\begin{matrix} P & Q & R & S (ii) & (iv) & (i) & (iii) \end{matrix}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

(P) $y = cos (3 {cos}^{- 1} x) \Rightarrow y' = \frac{3 sin (3 {cos}^{- 1} x)}{\sqrt{1 - x^{2}}}$
$\sqrt{1 - x^{2}} y' = 3 sin (3 {cos}^{- 1} x)$
$\Rightarrow \frac{- x}{\sqrt{1 - x^{2}}} y' + \sqrt{1 - x^{2}} y'' = 3 cos (3 {cos}^{- 1} x) \cdot \frac{- 3}{\sqrt{1 - x^{2}}}$
$\Rightarrow - x y' + (1 - x^{2}) y'' = - 9 y$
$\Rightarrow \frac{1}{y} [(x^{2} - 1) y'' + x y'] = 9$
(Q) Plan
(i) Angle subtended by a side of n sided regular polygon at the centre $= \frac{2 π}{n} .$
(ii) $| a \times b | = | a | | b | sin θ$
(iii) $| a \cdot b | = | a | | b | cos θ$
(iv) $tan θ = tan α \Rightarrow θ = n π + α, n \in Z$
Consider a polygon (S) of n sides with centre at orgin

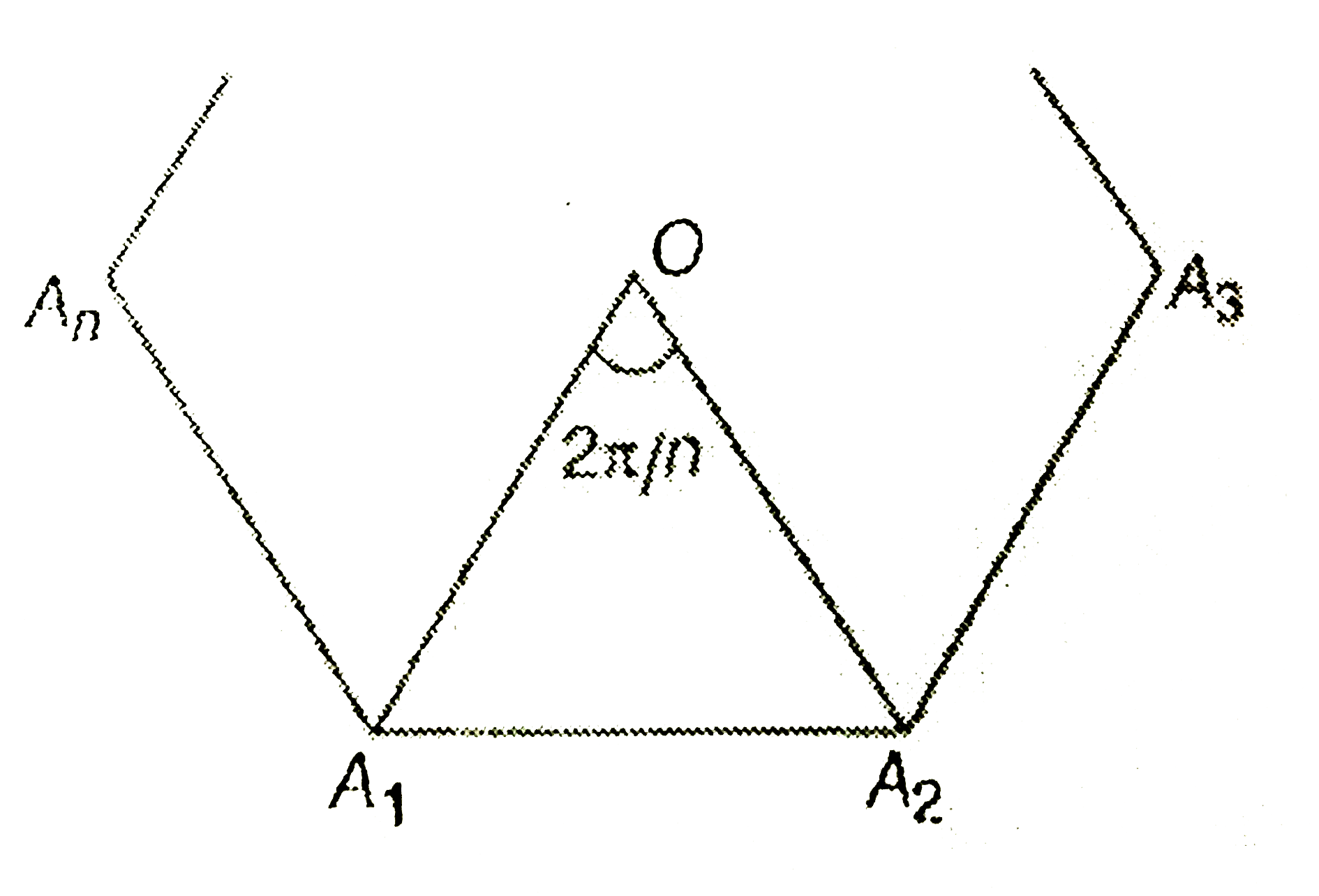
Let $| O A_{1} | = | O A_{2} | = ... | O A_{n} | = r [say]$
$| a_{k} \times a_{k + 1} | = r^{2} sin \frac{2 π}{n}$
$| a_{k} \cdot a_{k + 1} | = r^{2} cos \frac{2 π}{n}$
$\Rightarrow ∣ ∣ ∣ ∣ n - 1 \sum k = 1 a_{k} \times a_{k + 1} ∣ ∣ ∣ ∣ = ∣ ∣ ∣ ∣ n - 1 \sum k = 1 a_{k} \cdot a_{k + 1} ∣ ∣ ∣ ∣$
$\Rightarrow r^{2} (n - 1) sin \frac{2 π}{n} = r^{2} (n - 1) cos \frac{2 π}{n}$
$\Rightarrow tan \frac{2 π}{n} = 1 \Rightarrow tan \frac{2 π}{n} = tan \frac{π}{4}$
$\Rightarrow \frac{2 π}{n} = t π + \frac{π}{4}, t \in Z$
$\Rightarrow \frac{2}{n} = \frac{4 t + 1}{4} \Rightarrow n = \frac{8}{4 t + 1}, t \in Z$
$∴$ The minimum value of $n = 8$
(R) PLAN
Equation of normal at the point
$(a cos θ, b sin θ) of ellipse \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ is given by
$a x sec θ - by cosec θ = a^{2} - b^{2}$
Equation of normal is
$\sqrt{6} x sec θ - \sqrt{3} y cosec θ = 3$
Its slope is $\frac{\sqrt{6} sec θ}{\sqrt{3} cosec θ} = 1$
$∵$ Slope of normal = Slope of line perpendicular to
$x + y = 8 ∴ tan θ = \frac{1}{\sqrt{2}}$
So, normal is $\sqrt{6} x \frac{\sqrt{3}}{\sqrt{2}} - \sqrt{3} \times \sqrt{3} y = 3$
$3 x - 3 y = 3 \Rightarrow x - y = 1$
At it passes through (h, 1).
$∴ h - 1 = 1 \Rightarrow h = 2$
(S) Plan ${tan}^{- 1} x + {tan}^{- 1} y = {tan}^{- 1} (\frac{x + y}{1 - x y})$
Given equation
${tan}^{- 1} (\frac{1}{2 x + 1}) + {tan}^{- 1} (\frac{1}{4 x + 1}) = {tan}^{- 1} (\frac{2}{x^{2}})$
$\Rightarrow {tan}^{- 1} ⎡ ⎢ ⎣ \frac{\frac{1}{2 x + 1} + \frac{1}{4 x + 1}}{1 - \frac{1}{(2 x + 1) (4 x + 1)}} ⎤ ⎥ ⎦ = {tan}^{- 1} (\frac{2}{x^{2}})$
$\Rightarrow {tan}^{- 1} [\frac{6 x + 2}{(2 x + 1) (4 x + 1) - 1}] = {tan}^{- 1} (\frac{2}{x^{2}})$
$\Rightarrow \frac{3 x + 1}{4 x^{2} + 3 x} = \frac{2}{x^{2}} \Rightarrow 3 x^{3} + x^{2} = 8 x^{2} + 6 x$
$\Rightarrow x (3 x^{2} - 7 x - 6) = 0$
$\Rightarrow x (x - 3) (3 x + 2) = 0 \Rightarrow x = 0, \frac{- 2}{3}, 3$
So, only positive solution is $x = 3 .$
$(P) \to (i v), (Q) \to (i i i), (R) \to (i i), (S) \to (i)$

Updated on:21/07/2023

|

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

IIT JEE PREVIOUS YEAR-MISCELLANEOUS-MISCELLANEOUS

Home
Ask Doubt
Profile