Match the statements/expressions given in Column I with the given in Column II.

The correct Answer is:A→q,B→q,C→r
(A) Given, ∞∑i=1tan−1(12i2)=t=∞∑i=1tan−1(24i2−1+1)
⇒∞∑i=1tan−1{(2i+1)−(2i−1)1+(2i−1)(2i+1)}
⇒(tan−13−tan−11)+(tan−15−tan−13)+...+{tan−1(2n+1)−tan−1(2n−1)}
∴t=limn→∞{tan−1(2n+1)−tan−11}
=limn→∞tan−1(2n1+2n+1)=π4
⇒tant=1
(B) We have, cosθ1=1−tan2θ121+tan2θ12=ab+c
Applying componendo and dividendo,
tan2θ12=b+c−ab+c+a
Also, cosθ3=1−tan2θ321+tan2θ32=ca+b
Applying componendo and dividendo,
tan2θ32=a+b−ca+b+c
∴tan2θ12+tan2θ32=2ba+b+c=2b3b=23
[∵a,b,c are in an AP,so2b=a+c]
(C) Line through (0, 1, 0) and perpendicular to plane
x+2y+2z=0 is given by
x−01=y−12=z−02=r [say]
Any point on the line P(r,2r+1,2r) be the foot of perpendicular on the straight line, then
r⋅1+(2r+1)⋅2+(2r)⋅2=0
⇒r=−29
∴ Coordinates of P(−29,59,−49).
Hence, required perpendicular distance
=√4+25+1681=√53 unit
Topper's Solved these Questions
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - MISCELLANEOUSEXERCISE - MISCELLANEOUS87videos
MISCELLANEOUS
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - MATRICES AND DETERMINANTSEXERCISE - SOLVING SYSTEM OF EQUATIONS (INTEGER ANSWER TYPE QUESTION)2videos
MATRICES AND DETERMINANTS
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - PARABOLAEXERCISE - TOPIC 4 DIAMETER, CHORD OF CONTACT, CHORD BISECTED AND PRODUCT OF PAIR OF TANGENTS OBJECTIVES QUESTION II (ANALYTICAL & DESCRIPTIVE )5videos
PARABOLA
Similar Questions
Match the statements/expressions given in Column I with the values given in Column II.
 View Solution
View SolutionMatch the statements/expressions given in Column I with the values given in Column II. '
 View Solution
View SolutionMatch the statements/expressions given in Column I with the values given in Column II.
 View Solution
View SolutionMatch the statements/expressions given in Column I with the values given in Column II.
 View Solution
View SolutionMatch the statements/expressions given in Column I with the values given in Column II.
 View Solution
View SolutionMatch the statement given in Column I with the phenomenon given in Column II.
 View Solution
View SolutionMatch the statement given in Column I with the phenomenon given in Column II.
 View Solution
View SolutionMatch the statement given in Column I. with the phenomenon given in column II.
View SolutionMatch the reactions given in Column I with the names given in Column II.
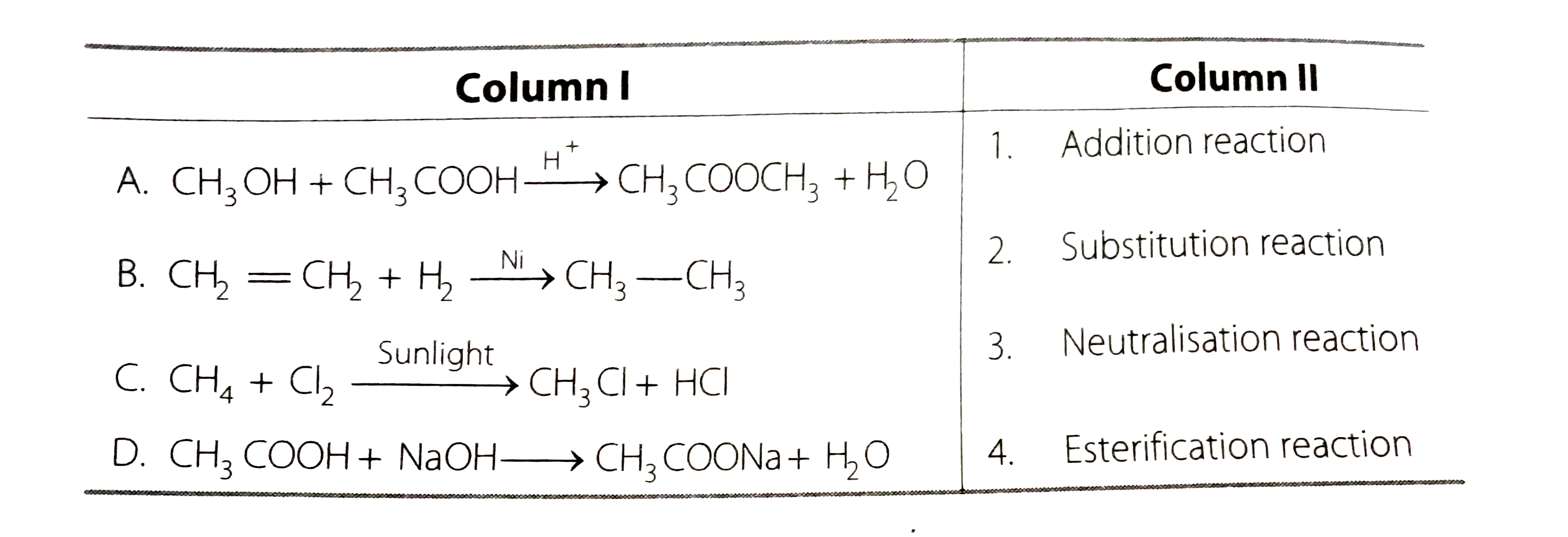 View Solution
View SolutionMatch the reactions given in Column I with the names given in Column II.
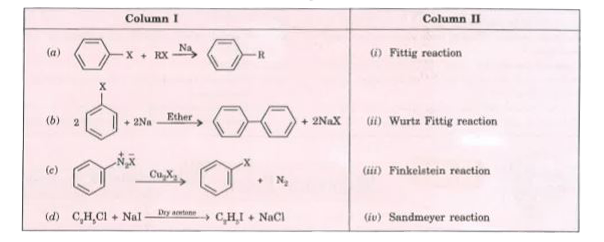 View Solution
View Solution

