Match the statements/expressions given in Column I with the given in Column II.

The correct Answer is:A→p,q,s,B→p,t;C→q,r,st;D→s
(A) Given, (x−3)2⋅y'+y=0
⇒dydx=y(x−3)2⇒∫dyy=−∫dx(x−3)2)
⇒Iny=1(x−3)+InC⇒y=Ce1x−3,C≠0
∴ Domain of y is x∈R−{3}
Alternate Solution Given differential equation is homogneous linear differential equation and has x = 3 as a singular point, hence x = 3 cannot be in domain of solution.
(B) Let I=∫51(x−1)(x−2)(x−3)(x−4)(x−5)dx
Let x−3=t
⇒dx=dt
∴I=∫2−2(t+2)(t+1)t(t−1)(t−2)dt
Q Integrand is an odd function.
∴I=0
Alternate Solution Let
I=∫51(x−1)(x−2)(x−3)(x−4)(x−5)dx ...(i)
Using , ∫baf(x)dx=∫baf(a+b−x)dx
I=∫51(5−x)(4−x)(3−x)(2−x)(1−x)dx ...(ii)
On adding Eqs. (i) and (ii), we get
2I=0⇒I=0
(C ) Let f(x)=cos2x+sinx
f'(x)=−2cosxsinx+cosx
=cosx(1−2sinx)=0 [say]
Sign sheme for first derivative
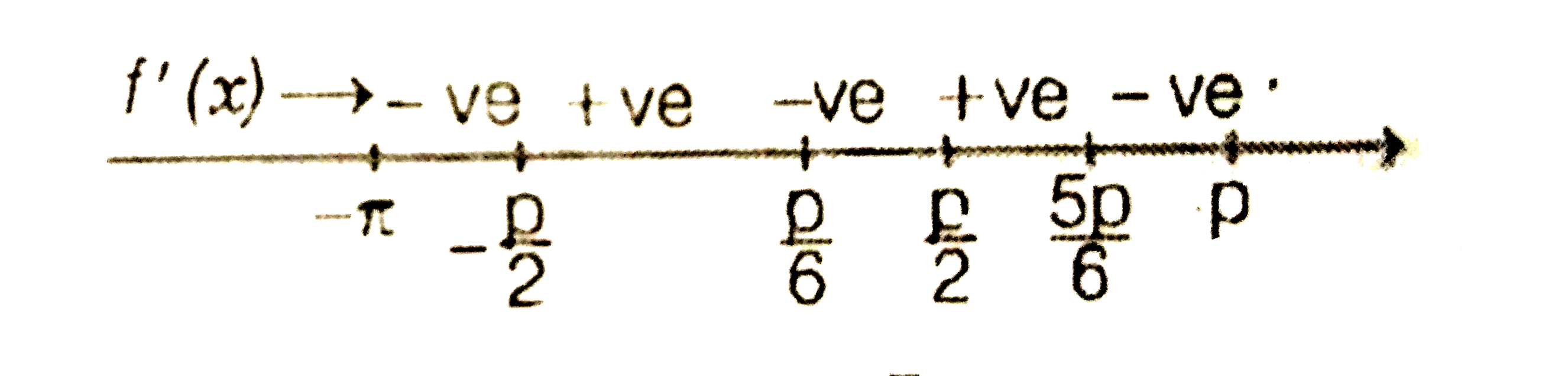
Points of local maxima are π6,5π6.
Alternate Solution y=cos2x+sinx
y=54−(sinx−12)2
For y to be maximum. (sinx−12)2=0
⇒sinx=12⇒x=nπ+(−1)nπ6,n∈I
(D) Let y=tan−1(sinx+cosx)
dydx=cosx−sinx1+(sinx+cosx)2
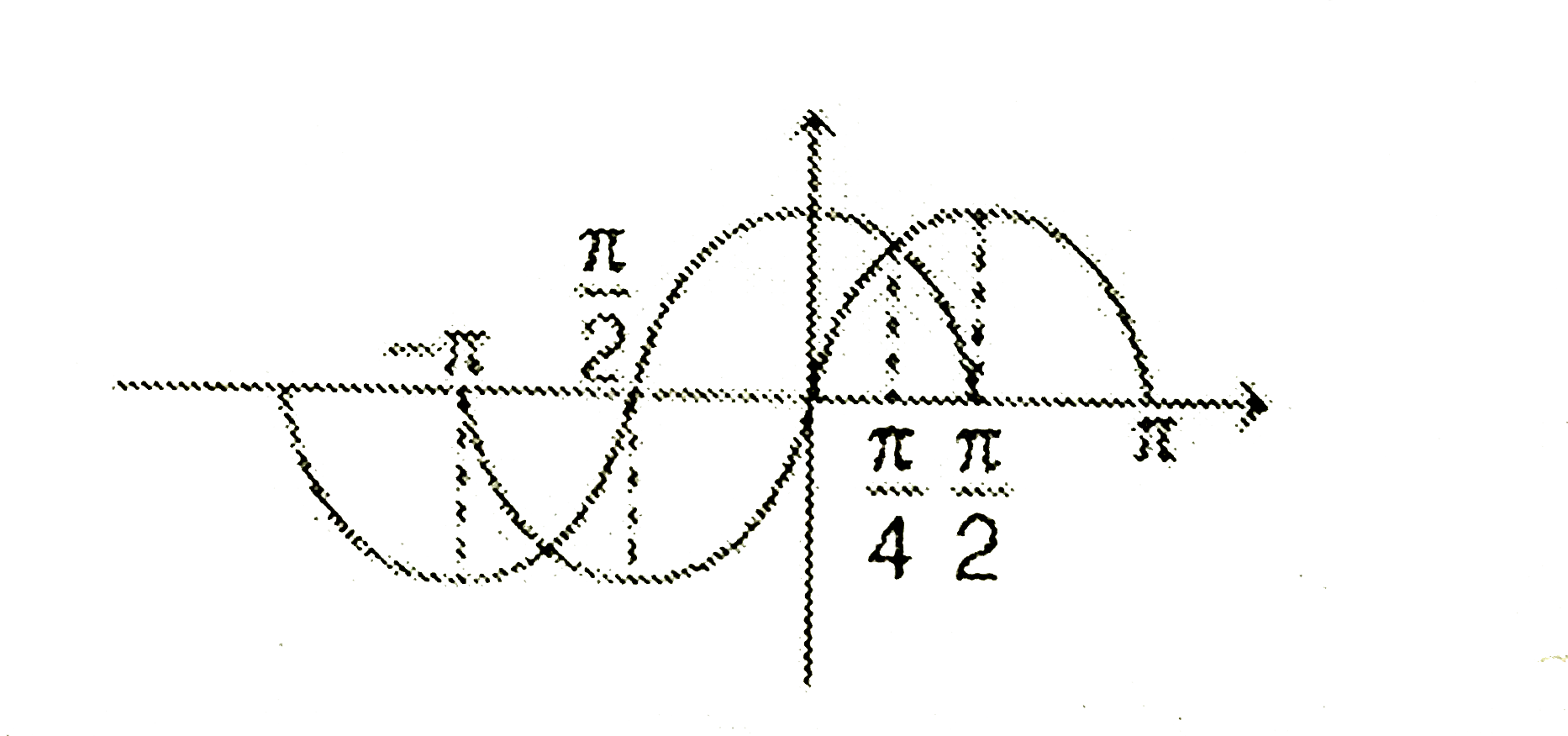
Clearly, by graph cosx>sinx is true for option (s).
Topper's Solved these Questions
- MISCELLANEOUSBOOK - IIT JEE PREVIOUS YEARCHAPTER - MISCELLANEOUSEXERCISE - MISCELLANEOUS
87 Videos
- MATRICES AND DETERMINANTSBOOK - IIT JEE PREVIOUS YEARCHAPTER - MATRICES AND DETERMINANTSEXERCISE - SOLVING SYSTEM OF EQUATIONS (INTEGER ANSWER TYPE QUESTION)
2 Videos
- PARABOLABOOK - IIT JEE PREVIOUS YEARCHAPTER - PARABOLAEXERCISE - TOPIC 4 DIAMETER, CHORD OF CONTACT, CHORD BISECTED AND PRODUCT OF PAIR OF TANGENTS OBJECTIVES QUESTION II (ANALYTICAL & DESCRIPTIVE )
5 Videos
Similar Questions
Match the statements/expressions given in Column I with the values given in Column II.

View SolutionMatch the statements/expressions given in Column I with the values given in Column II. '

View SolutionMatch the statements/expressions given in Column I with the values given in Column II.

View SolutionMatch the statements/expressions given in Column I with the values given in Column II.

View SolutionMatch the statements/expressions given in Column I with the values given in Column II.

View SolutionMatch the statement given in Column I with the phenomenon given in Column II.

View SolutionMatch the statement given in Column I with the phenomenon given in Column II.

View SolutionMatch the statement given in Column I. with the phenomenon given in column II.
View SolutionMatch the reactions given in Column I with the names given in Column II.
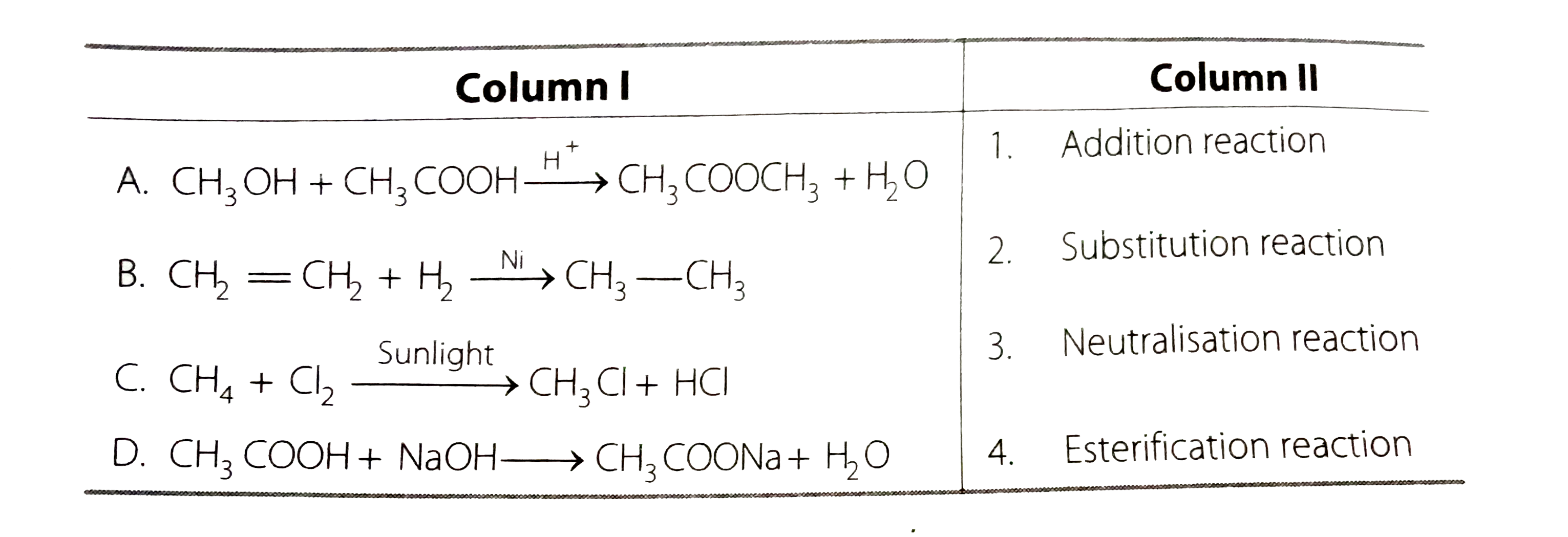
View SolutionMatch the reactions given in Column I with the names given in Column II.
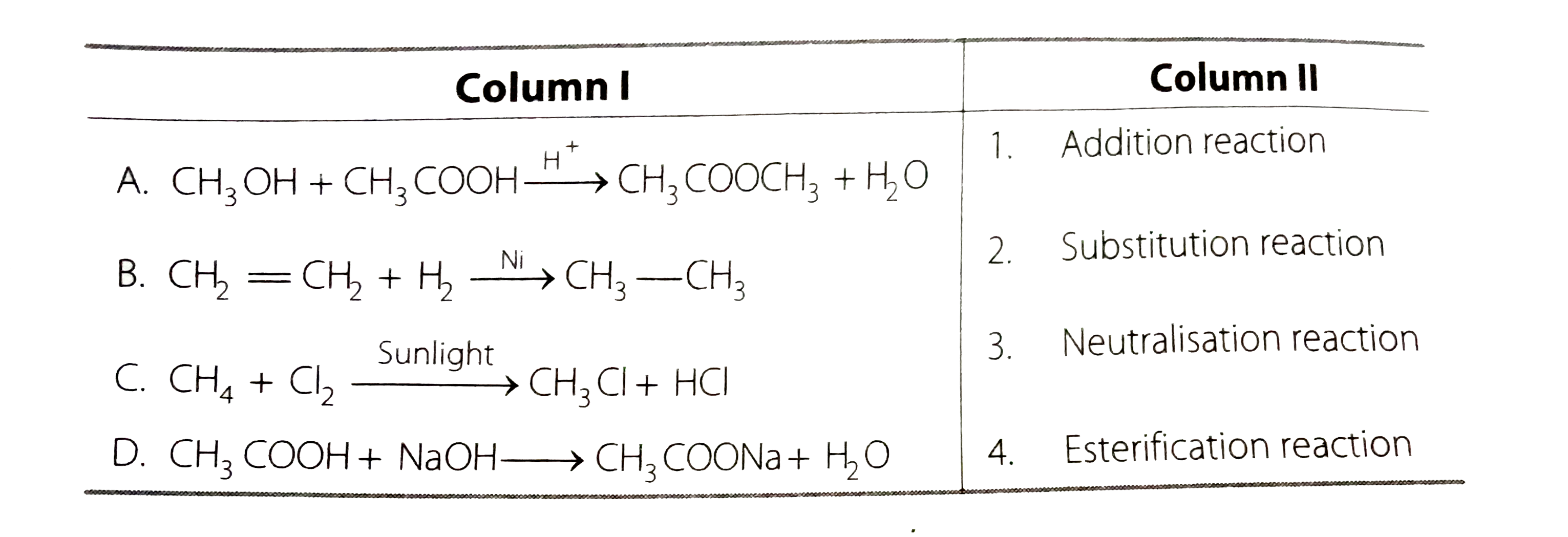
View Solution
