The total number of distinct $x \in (0, 1]$ for which $x \int 0 \frac{t^{2}}{1 + t^{4}} d t = 2 x - 1$ is

Video Solution

Text Solution

Verified by Experts

The correct Answer is:1

Let $f (x) = \int_{0}^{x} \frac{t^{2}}{1 + t^{4}} d t \Rightarrow f' (x) = \frac{x^{2}}{1 + x^{4}} > 0, for all x \in [0, 1]$
$∴ f (x)$ is increasing.
At $x = 0, f (0) = 0 and at x = 1$ ,
$f (1) = \int_{0}^{1} \frac{t^{2}}{1 + t^{4}} d t$
Because, $0 < \frac{t^{2}}{1 + t^{4}} < \frac{1}{2} \Rightarrow \int_{0}^{1} 0 \cdot d t < \int_{0}^{1} \frac{t^{2}}{1 + t^{4}} d t < \int_{0}^{1} \frac{1}{2} \cdot d t$
$\Rightarrow 0 < f (1) < \frac{1}{2}$
Thus, f(x) can be plotted as

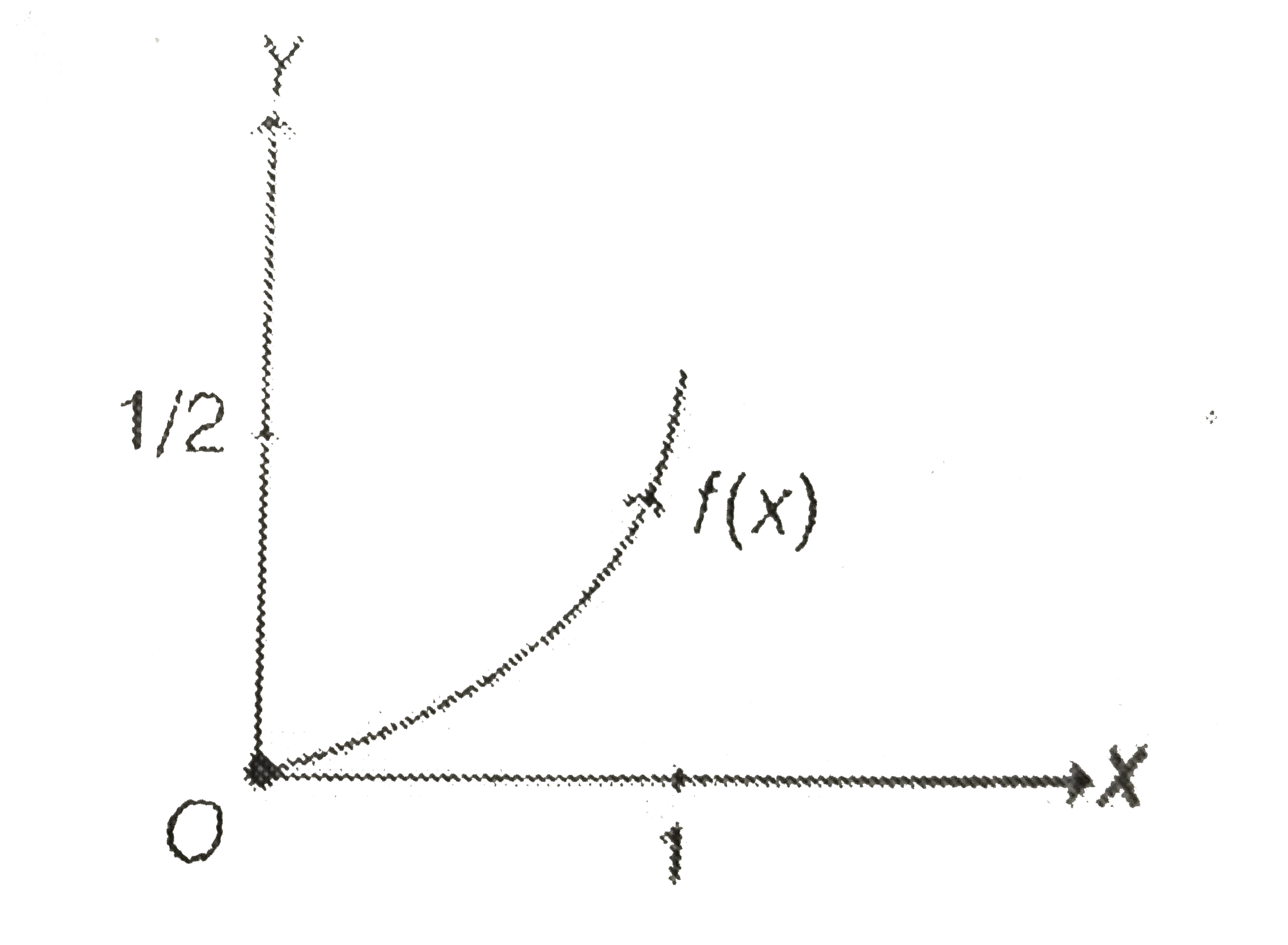
$∴ y = f (x) and y = 2 x - 1$ can be shown as

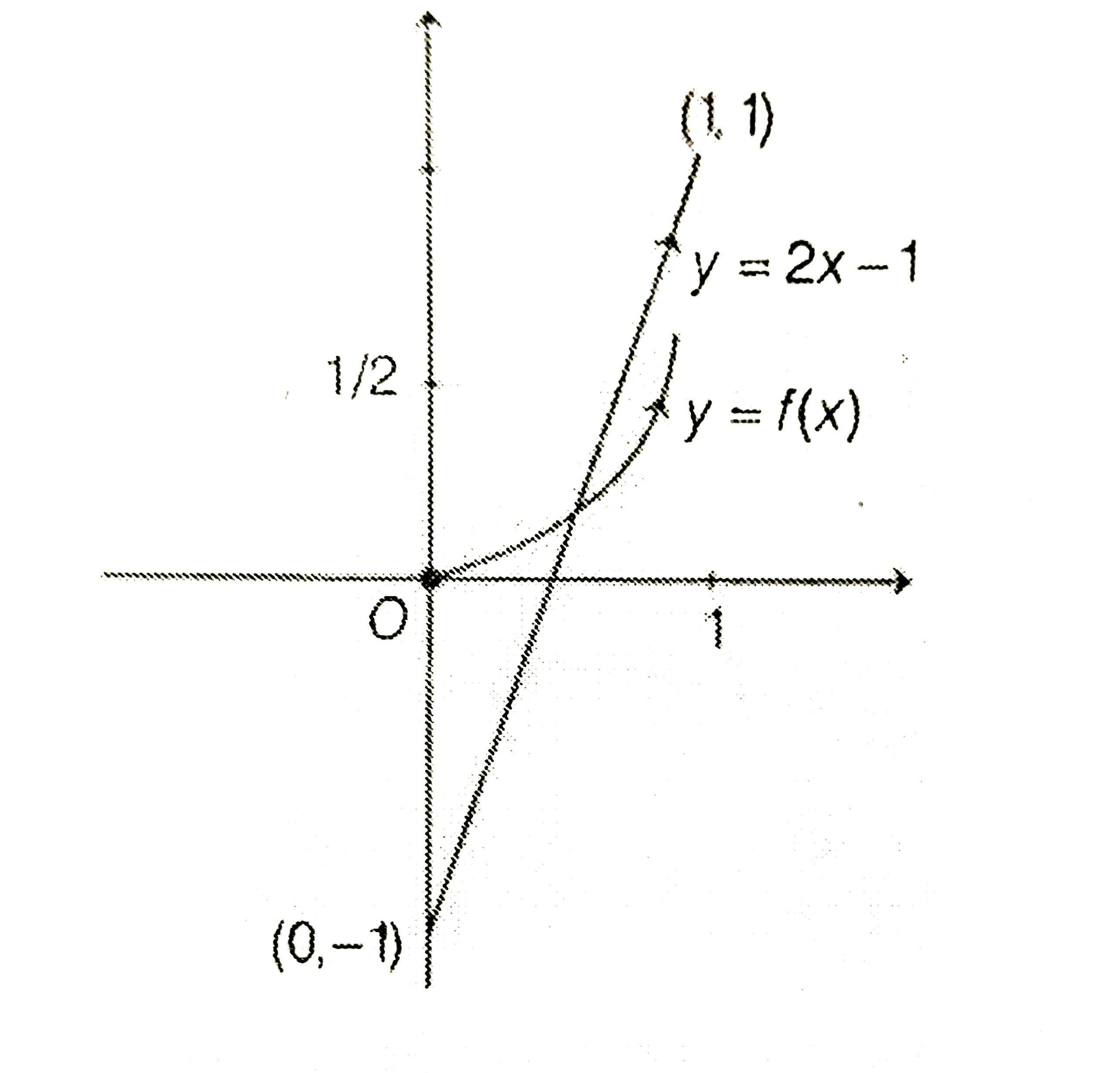
From the graph, the total number of distinct solutions for $x \in (0, 1] = 1 .$ [as they intersect only at one point]

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If $f (x) = \int_{2}^{x} \frac{d t}{1 + t^{4}}$ , then
A $f (3) < \frac{1}{17}$
B $f (3) > \frac{1}{17}$
C $f (3) = \frac{1}{17}$
D $f (3) > 1$
Question 2 - Select One
Consider the function f : $(- \infty, \infty) \to (- \infty, \infty)$ defined by f(x) = $\frac{x^{2} - a x + 1}{x^{2} + a x + 1}, 0 < a < 2$
Let $g (x) = e^{x} \int 0 \frac{f' (t)}{1 + t^{2}}$ dt
Which of the following is true ?
Ag'(x) is positive on $(- \infty, 0)$ and negative on $(0, \infty)$
Bg'(x) is negative on $(- \infty, 0)$ and positive on $(0, \infty)$
Cg'(x) changes sign on both $(- \infty, 0)$ and $(0, \infty)$
Dg'(x) does not change sign on $(- \infty, \infty)$
Question 3 - Select One
For $x \in (0, \frac{5 π}{2})$ define
f(x) = $x \int 0 \sqrt{t} sin t d t$
Then has :
Alocal maximum at $π$ and $2 π$
Blocal minima at $π$ and $2 π$
Clocal maximum at $π$ and local maximum at $2 π$
Dlocal maximum at $π$ and local minimum at $2 π$

IIT JEE PREVIOUS YEAR-MISCELLANEOUS-MISCELLANEOUS

Home
Ask Doubt
Profile