ABCD is a parallelogram in which BC is produced to E such that CE = BC. AE intersects CD at F.
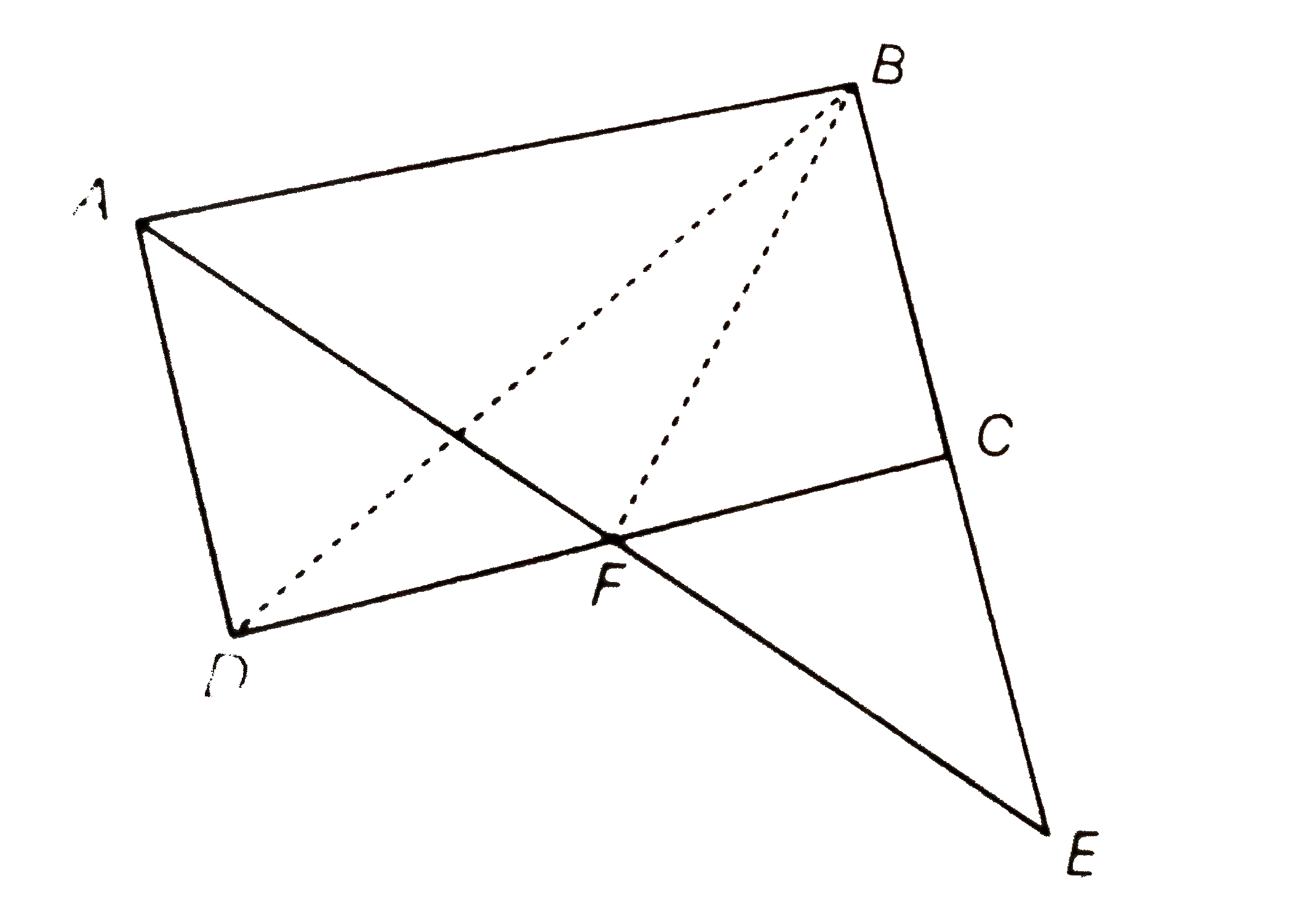
If ar(ΔDFB)=3cm2, then find the area of the parallelogram ABCD.
The correct Answer is:28cm2
△MDA≅MCP [∴∠DMA=∠CMP,∠MDA=∠MCP,AD=CP since AD=BCandCP=BC]
∴DM=MC (c.p.c.t) and so BM is a median of △BDC.
Thus, ar(DMB)=12ar(BDC).
But, ar(BDC)=12ar(ABCD) [∴ BD is a diagonal of ||gm ABCD].
∴ar(DMB)=14ar(ABCD) and so ar(ABCD)= 28 cm^(2).
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)32videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE5videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE5videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)16videos
AREAS OF TRIANGLES AND QUADRILATERALS
Similar Questions
Knowledge Check
- Question 1 - Select One
ABCD is a parallelogram. BC is produced to Q such that BC = CQ. Then
A(a) area (ΔBCP) = area (ΔDPQ)B(b) area (ΔBCP)> area (ΔDPQ)C(c) area (ΔBCP)< area (ΔDPQ)D(d) area (ΔBCP) + area (ΔDPQ) = area (ΔBCD) - Question 2 - Select One
In a parallelogram ABCD, a side AB is extended to E such that BE = AB. If DE cut the line BC at Q then point Q divide BC in what ratio?
A1:2B1:1C2:3D2:1
The side AD of parallelogram ABCD is produced to a point E. BE intersects CD at F. Show that ΔABE~ΔCFB.
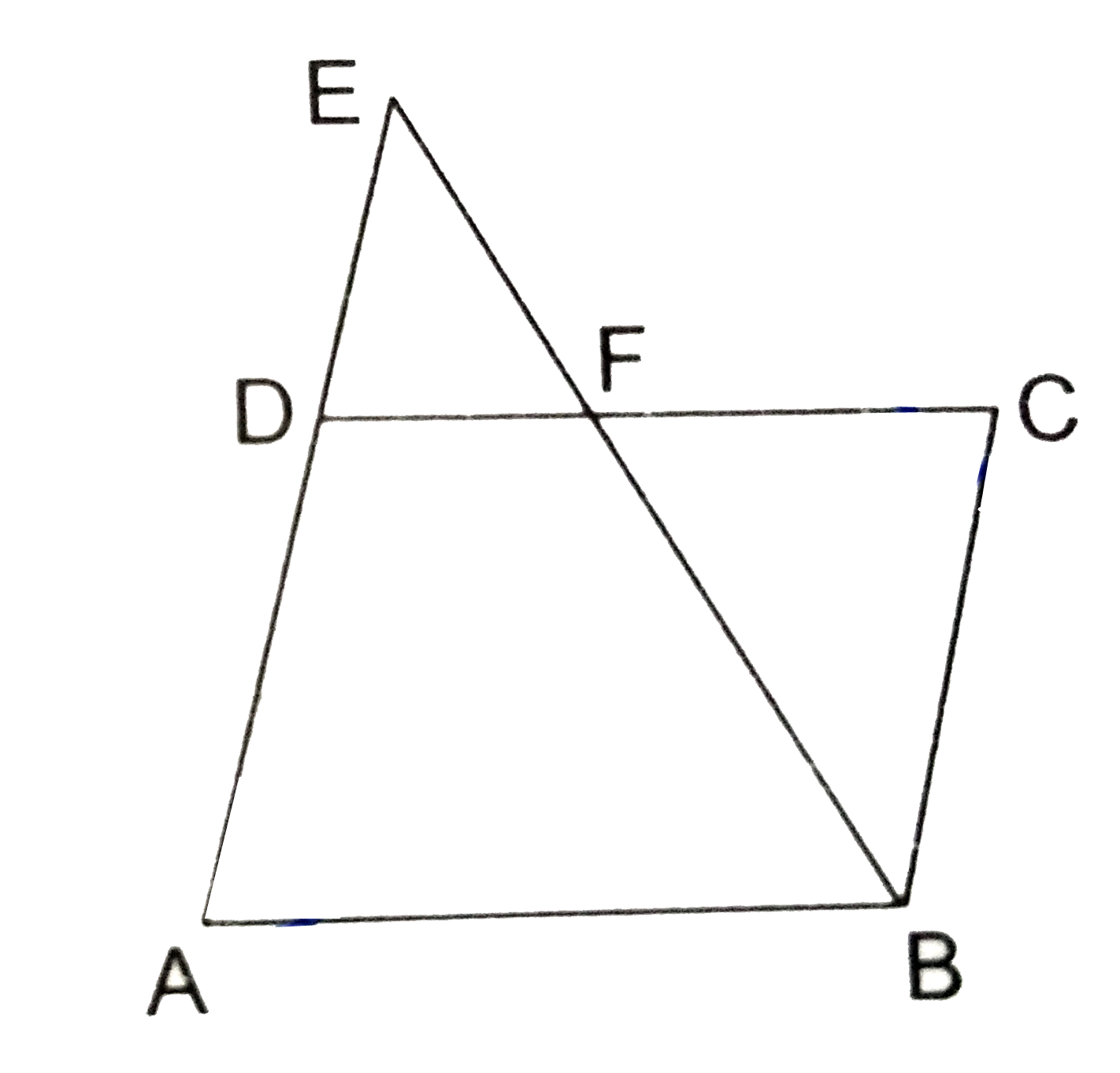 View Solution
View SolutionIn the given figure, ABCD is a parallelogram in which DC is extended to F such that AF intersects BC at E . Then perimeter of ΔABE=
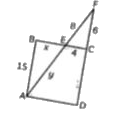 View Solution
View SolutionIn the figure, ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that ar(ΔBPC) = ar(ΔDPQ).
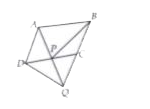 View Solution
View SolutionABCD is a parallelogram, P is the mid point of AB. BD and CP intersects at Q such that CQ:QP=3:1. If ar(ΔPBQ)=10cm2, find the area of parallelogram ABCD.
View SolutionABCD is a parallelogram. The circle through A,B and intersects CD produced at E. show that AD =AE.
View SolutionABCD is a parallelogram. The circle through A,BandC intersects CD produced at E, prove that AE=AD.
View Solution

