In a trapezium ABCD, AB || DC, AB = a cm, and DC = b cm. If M and N are the midpoints of the nonparallel sides, AD and BC respectively then find the ratio of ar(DCNM) and ar(MNBA).

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $(a + 3 b) : (3 a + b)$

M and N are midpoints of AD and BC respectively
$\Rightarrow$ MN||AB||DC and MN $= \frac{1}{2} (A B + D C) = (\frac{a + b}{2})$ .
Draw $D Q ⊥ A B$ . Let DQ cut MN at P.
Then, P is the midpoint of DQ,
i.e., DP = PQ = h (say).
Now, $a r (D C N M) = \frac{1}{2} \times (D C + M N) \times D P = \frac{1}{2} = \frac{1}{2} \times (b + \frac{a + b}{2}) \times h = \frac{h}{4} \times (a + 3 b)$
and $a r (M N B A) = \frac{1}{2} \times (M N + A B) \times P Q = \frac{1}{2} \times (\frac{a + b}{2} + a) \times h = \frac{h}{4} \times (3 a + b)$ .
$∴ a r (D C N M) : a r (M N B A) = (a + 3 b) : (3 a + b)$ .

Updated on:21/07/2023

|

Class 9 MATHS AREA OF PARALLELOGRAMS AND TRIANGLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

In figure, if DE $| |$ BC, then find the ratio of ar ( $Δ A D E$ ) and ar(DECB).

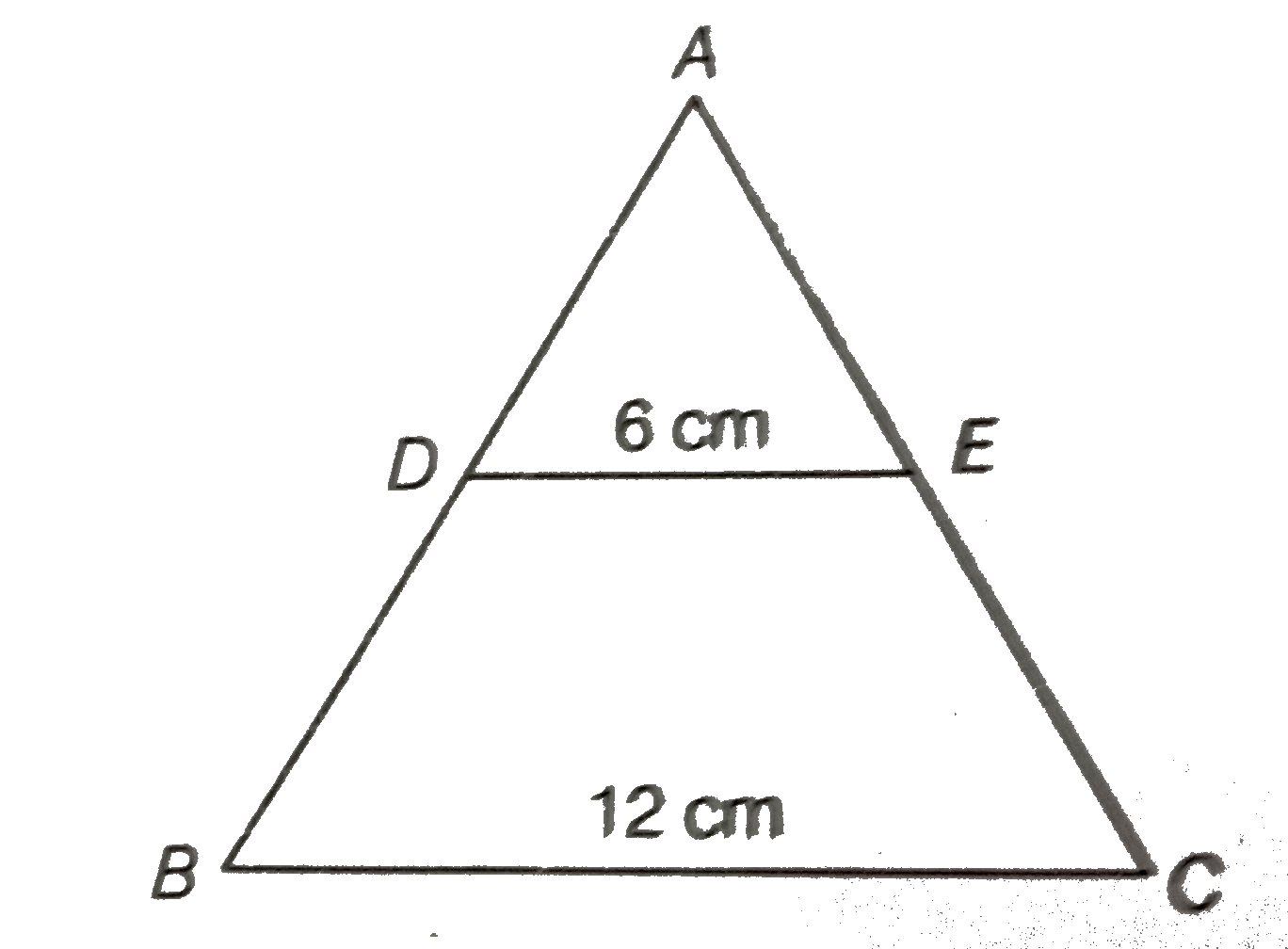A $1 : 3$
B $1 : 2$
C $2 : 5$
D $3 : 5$
ABCD is a trapezium in which AB || DC a and DC= 40 cm and AB = 60 cm. If X and Y a re respectively, the midpoints of AD and BC, then

XY=
A40 cm
B50 cm
C60 cm
D30 cm
In a trapezium ABCD, AB||DC, AB = AD, $∠ A D C = 64^{\circ} and ∠ B C D = 54^{\circ}$ . Find $∠ D B C$ .

A $64^{\circ}$
B $72^{\circ}$
C $94^{\circ}$
D $116^{\circ}$

RS AGGARWAL-AREAS OF PARALLELOGRAMS AND TRIANGLES -Exercise 11

Home
Ask Doubt
Profile