In figure X and Y are the mid-points of AC and AB respectively, QP∣∣BC and CYQ and BXP are straight lines. Prove that ar(ΔABP)=ar(ΔACQ).
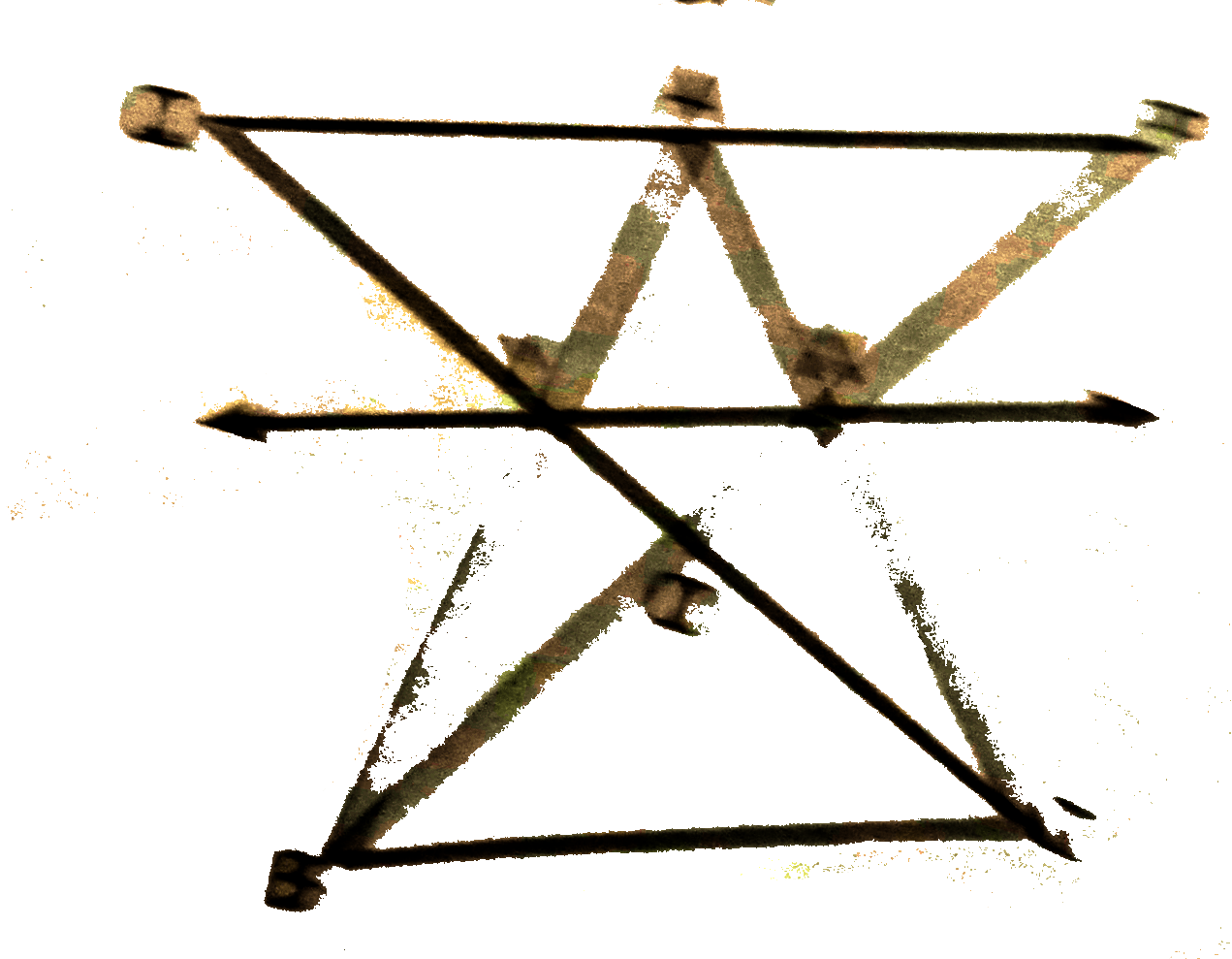
In △PAC, we have PA||DE and E is the midpoint of AC.
∴ D is the midpoint of PC (by converse of midpoint theorem).
And so, DE=12PA, i.e., PA=2(DE).
Similarly, AQ = 2(DE) and so, PA=AQ.
Now, ar(△ABQ)=ar(△ACP)
[∴△ABQand△ACP have equal base and lie between the same parallels].
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)32videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE5videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE5videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)16videos
AREAS OF TRIANGLES AND QUADRILATERALS
Similar Questions
Knowledge Check
- Question 1 - Select One
In △ABC, M,N and P are the mid-points of AB,AC and BC respectively. If MN=3cm,NP=3.5cm and MP=2.5cm, calculate BC,AB and AC.
ABC = 6 cm
AB = 7cm
AC = 5cmBBC = 6 cm
AB = 7cm
AC = 8cmCBC = 6 cm
AC = 7cm
AB = 5cmDnone of these
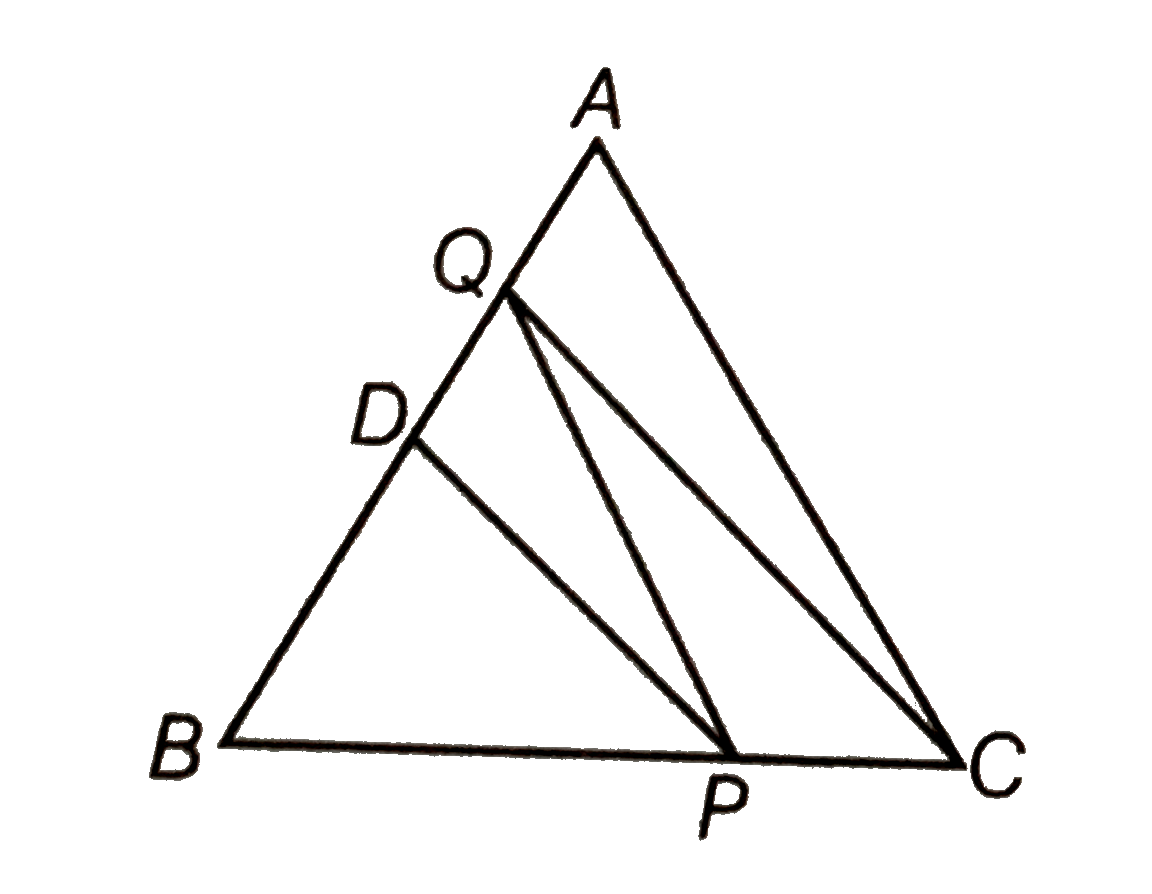
In Δ ABC, D is the mid-point of AB and P is any point on BC. If CQ∣∣PD meets AB and Q (shown in figure), then prove that
ar(ΔBPQ)=12ar(ΔABC).
 View Solution
View SolutionIn Figure O is the mid-point of aB and CD. Prove tat AC=BD and AC||BD.
 View Solution
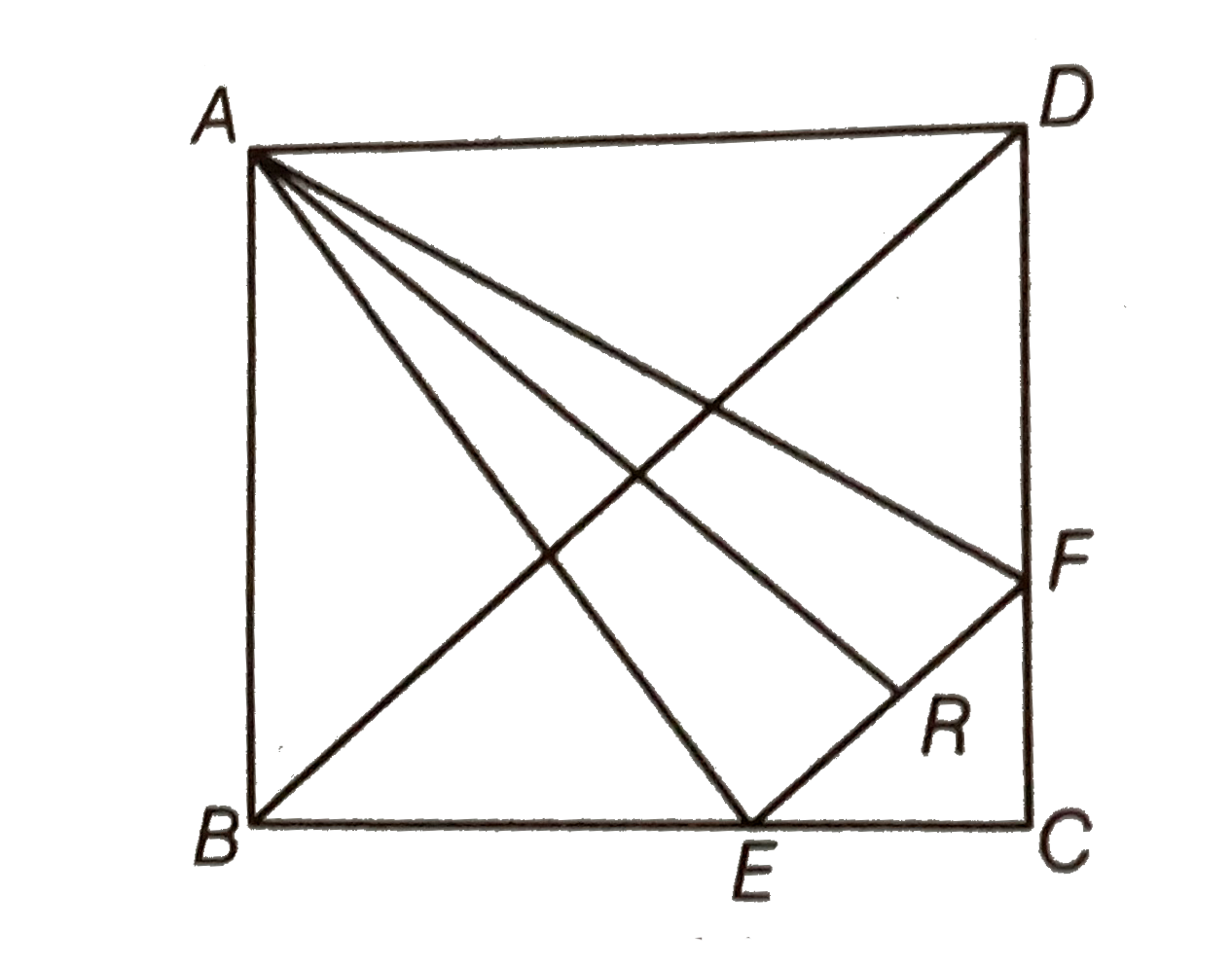
View SolutionABCD is a square. E and F are respectively the mid-points of BC and CD. If R is the mid-point of EF, prove that ar(ΔAER)=ar(ΔAFR).
 View Solution
View SolutionP and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that
ar(ΔPRQ) = 1/2 ar(ΔARC)View SolutionIn the adjoining figure , we have X and Y are the mid - point of AC and BC and AX = CY . Show that AC =BC.
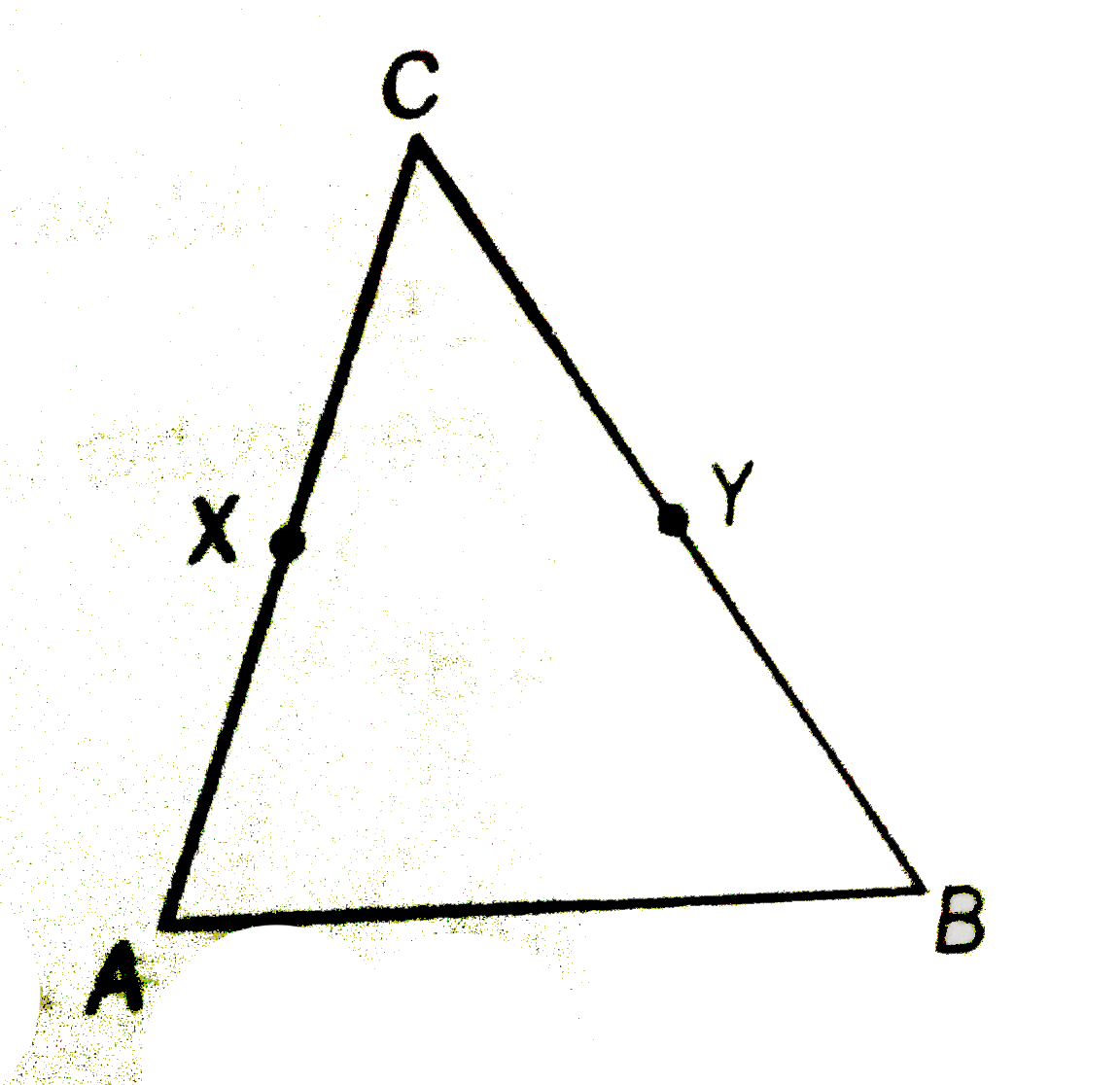 View Solution
View SolutionIf the given figure , M, N and P are the mid-points of AB,AC and BC respectively. If MN=3 cm, NP=3.5 cm and MP=2.5 cm, calculate BC , AB and AC
 View Solution
View SolutionD and E are points on sides AB and AC respectively of ΔABC such that ar(ΔDBC) = ar(ΔEBC). Prove that DE I I BC.
View Solution


