The base BC of ΔABC is divided at D, so that BD=12DC. Prove that ar(ΔABD)=13ar(ΔABC)
Let E be the midpoint of DC. Then,
BD=DE=EC=13BC.
Join AD and AE.
In △ABE, AD is a median and so ar(△ABD)=ar(△ADE).
In △ADC, AE is a median and so ar(△ADE)=ar(△AEC).
∴ar(△ABD)=ar(△ADE)=ar(△AEC)=12ar(△ABC).

Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
32 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE
5 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE
5 Videos
- AREAS OF TRIANGLES AND QUADRILATERALSBOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
Similar Questions
The base BC of ΔABC is divided at D, so that BD=12DC.Prove that ar(ΔABD)=13ar(ΔABC)
View SolutionD is a point on the base BC of ΔABC.AD is produced upto E such that DE = AD. Prove that:
area of ΔBCE= area of ΔABC
View SolutionABCD is a trapezium in which AB I I DC. DC is produced to E such tha t CE= AB, prove that ar(ΔABD) = ar(ΔBCE).
View SolutionDiagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar(ΔAOD) = ar(ΔBOC).
View SolutionABCD is a trapezium with AB||DC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar(ΔADX) = ar(ΔACY).
View SolutionIn the same figure, ΔABCandΔDBC are on the same base BC . If AD is intersects BC at O, prove that
ar(ΔABC)ar(ΔDBC)=AODO
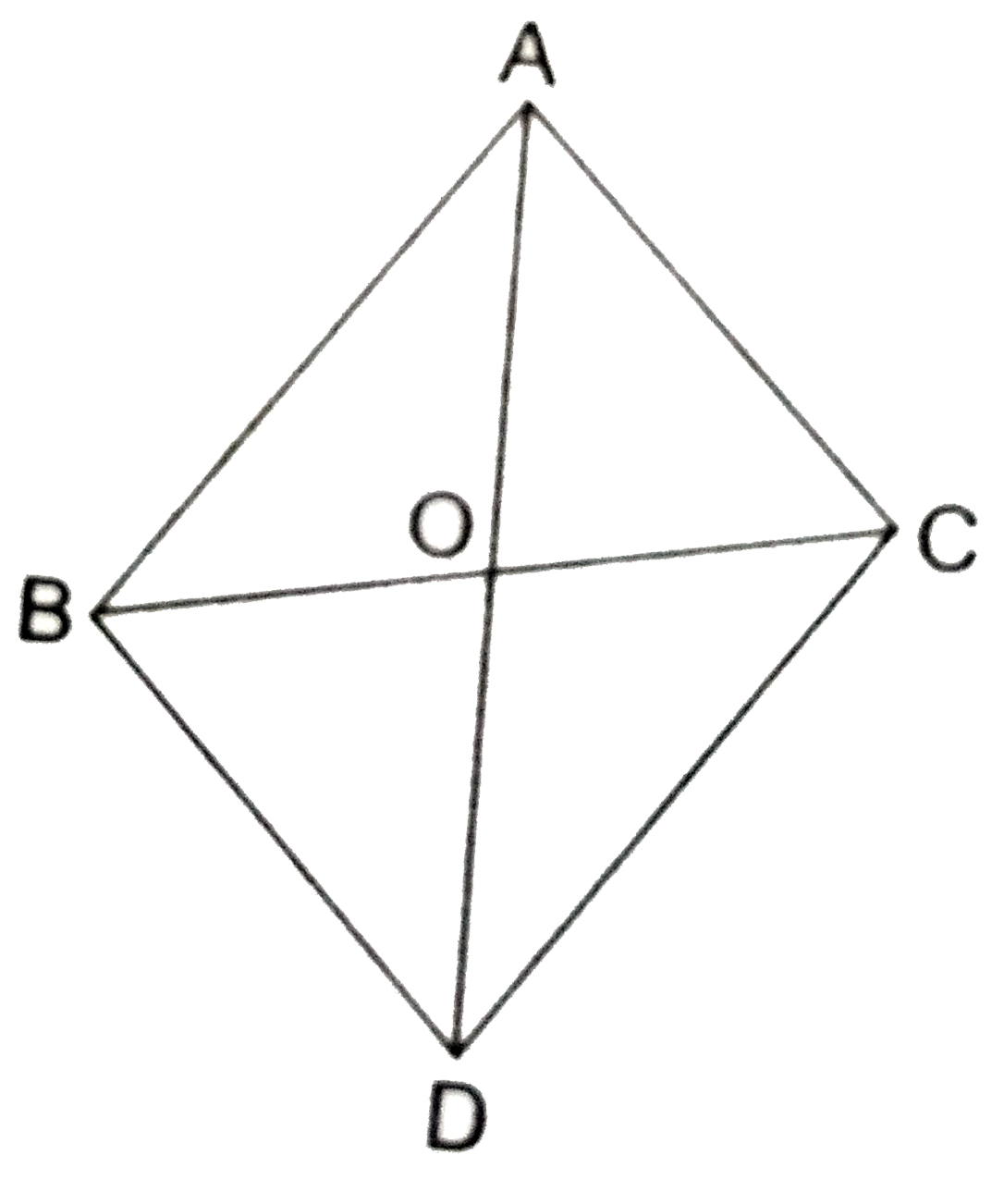
View SolutionIn the given figure, ΔABCandΔDBC have the same base BC. If AD and BC intersect at O, prove that ar(ΔABC)ar(ΔDBC)=AODO
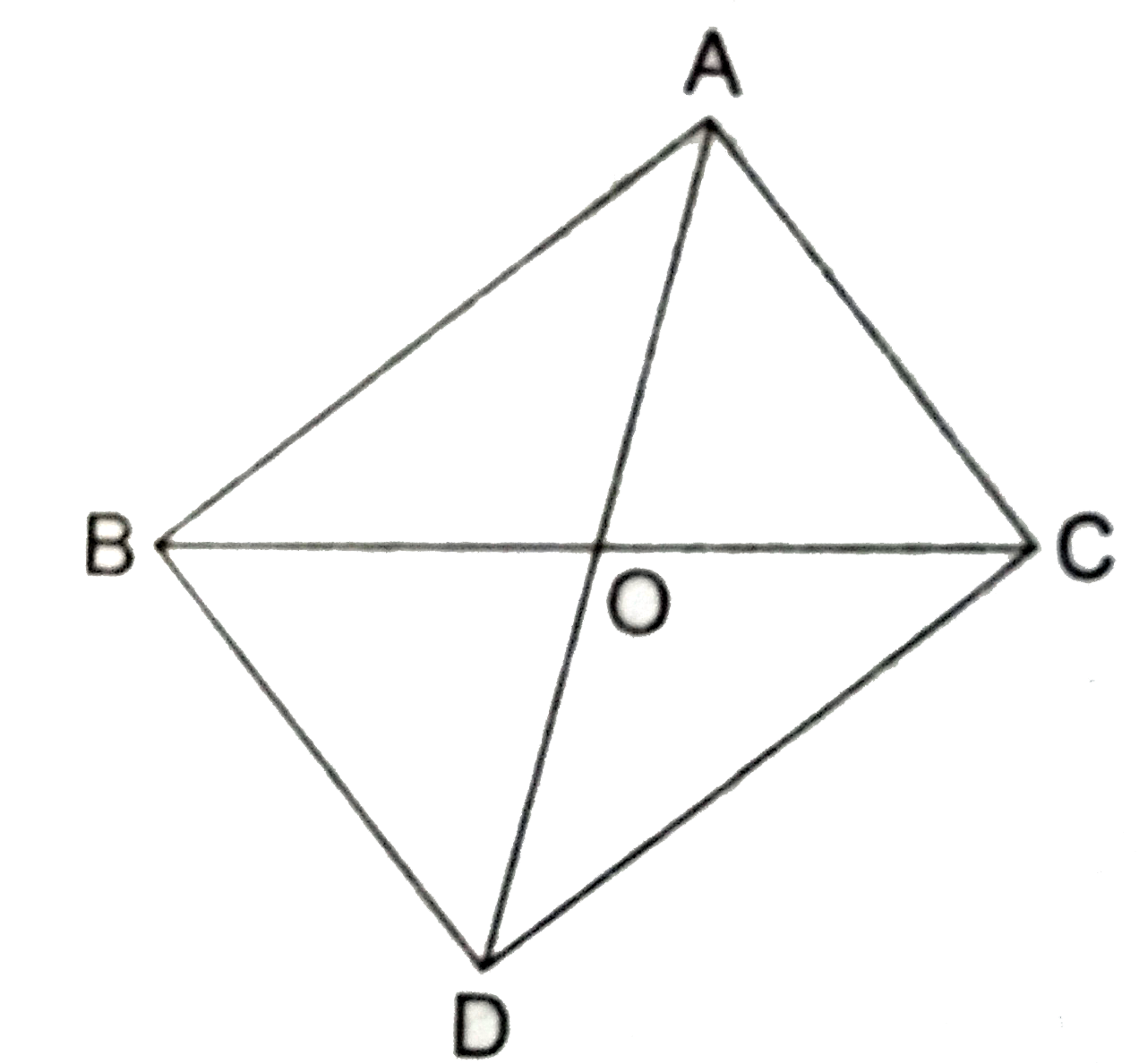
View SolutionIn ΔABC,ADandBE are altitudes. Prove that ar(ΔDEC)ar(ΔABC)=DC2AC2.
View SolutionIn the given figure, ΔABCandΔDBC are on the same base BC. If AD intersects BC at O, prove that ar(ΔABC)ar(ΔDBC)=AODO
View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
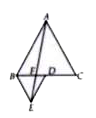
ar(ΔBDE) = 1/4 ar(ΔABC)
View Solution
