Heat Engine
Step-by-Step Solution for Heat Engine
1. Understanding Heat Engine: A heat engine is a device that converts heat energy into mechanical work. It operates between two thermal reservoirs: a hot source and a cold sink.
2. Labeling the Components:
- Identify the hot source (T1) that supplies heat (Q1) to the engine.
- Identify the cold sink (T2) where the engine rejects some heat (Q2).
- The engine performs work (W) during this process.
3. Energy Transfer:
- The heat engine absorbs heat (Q1) from the hot source.
- It converts part of this heat into work (W).
- The remaining heat (Q2) is expelled to the cold sink.
4. Work Done by the Engine:
- According to the first law of thermodynamics, the work done by the engine can be expressed as:
W=Q1−Q2
5. Efficiency of the Heat Engine:
- The efficiency (η) of the heat engine is defined as the ratio of the work done (W) to the heat absorbed (Q1):
η=WQ1
- Substituting the expression for W:
η=Q1−Q2Q1=1−Q2Q1
6. Carnot Engine Efficiency:
- For a Carnot engine, which operates on a reversible cycle, the efficiency can also be related to the temperatures of the hot and cold reservoirs:
Q2Q1=T2T1
- Therefore, the efficiency of a Carnot engine can be expressed as:
η=1−T2T1
- Here, T1 and T2 must be in Kelvin.
- Identify the hot source (T1) that supplies heat (Q1) to the engine.
- Identify the cold sink (T2) where the engine rejects some heat (Q2).
- The engine performs work (W) during this process.
- The heat engine absorbs heat (Q1) from the hot source.
- It converts part of this heat into work (W).
- The remaining heat (Q2) is expelled to the cold sink.
- According to the first law of thermodynamics, the work done by the engine can be expressed as:
W=Q1−Q2
- The efficiency (η) of the heat engine is defined as the ratio of the work done (W) to the heat absorbed (Q1):
η=WQ1
- Substituting the expression for W:
η=Q1−Q2Q1=1−Q2Q1
- For a Carnot engine, which operates on a reversible cycle, the efficiency can also be related to the temperatures of the hot and cold reservoirs:
Q2Q1=T2T1
- Therefore, the efficiency of a Carnot engine can be expressed as:
η=1−T2T1
- Here, T1 and T2 must be in Kelvin.
Similar Questions
A heat engine is a system that converts heat into mechanical work. A heat "source" generates thermal energy that brings a working substance to a high temperature. The working substance then generates work in the engine while transferring heat to a sink at a lower temperature . The working of a heat engine is shownn figure 1.
 Heat engines can be modelled using themodynamic cycles. The heat engine given in Figure -2 is of a working substance which is 1.00 mol of a monoatomic ideal gas . The thermodynamic cycle begins at the point designated as '1' and goes clockwise and the values of P and l or V at each point is as given below Fig-2 (P1=1.00atm and V1=24.6L,P2=2.00atm,V3=49.2L,P4=1.00atm)
Heat engines can be modelled using themodynamic cycles. The heat engine given in Figure -2 is of a working substance which is 1.00 mol of a monoatomic ideal gas . The thermodynamic cycle begins at the point designated as '1' and goes clockwise and the values of P and l or V at each point is as given below Fig-2 (P1=1.00atm and V1=24.6L,P2=2.00atm,V3=49.2L,P4=1.00atm)
Calculate T1,T2,T3andT4
View SolutionEven carnot heat engine cannot give 100% efficiency. Explain why
OR
can you design a heat engine of 100% efficiency? Explain ypur answer.
OR
A heat engine with 100% efficiency is only a theoretical possibility. Explain.
View Solution
Knowledge Check
Consider a heat engine as shown in (figure). Q1andQ2 are heat added to heat bath T1 and heat taken from T2 one cycle of engine. W is the mechanical work done on the engine.
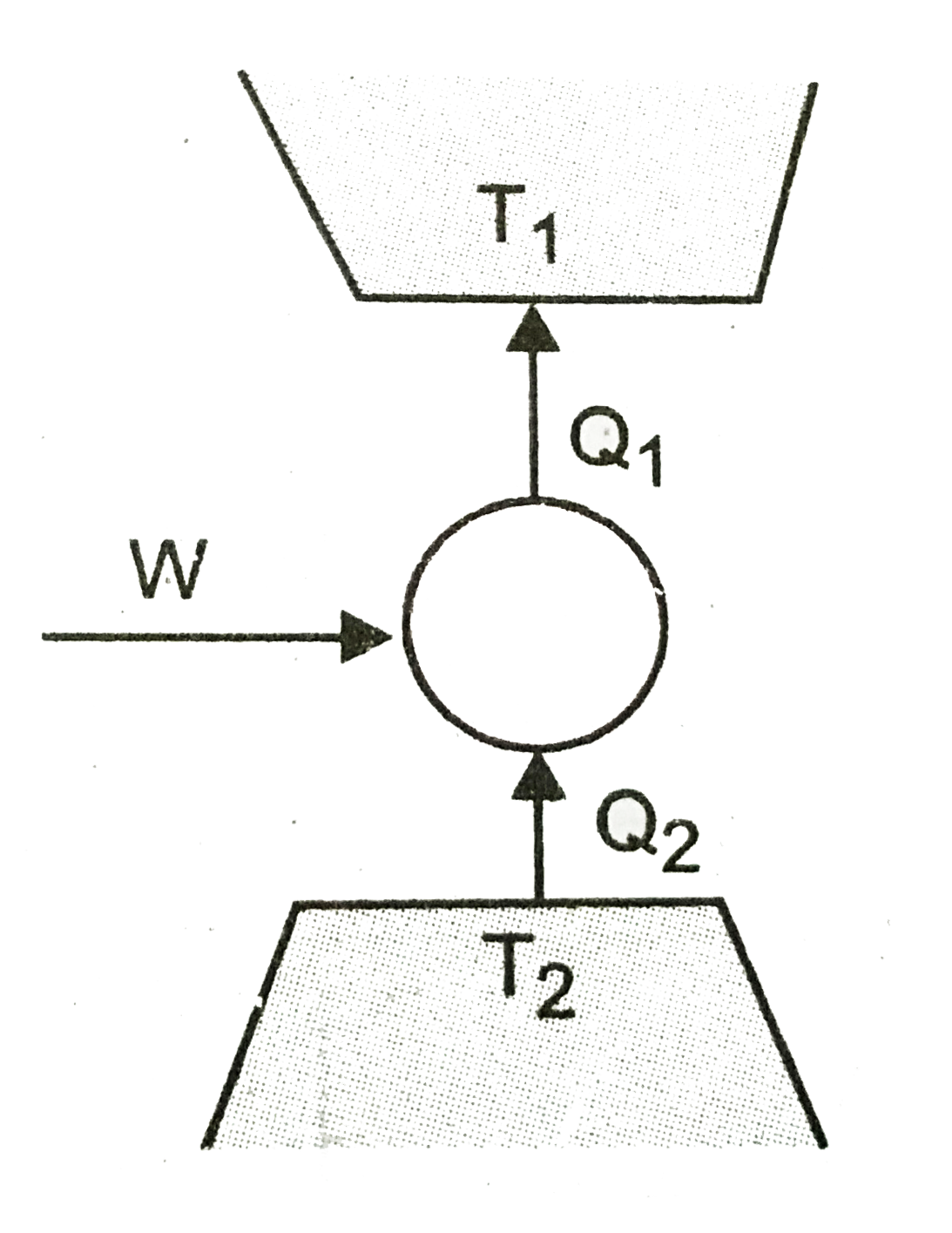
If W>0, then possibillities are:AQ1>Q2>0BQ2>Q1>0CQ2 < Q1 < 0DQ1<0,Q2>0
Two heat engines are operating in such a way that the heat rejected by the first engine is used as the heat input of the second. If both the engines are 40% efficient, then the overall efficiency of the system is
View SolutionConsider a heat engine as shown in figure. Q1andQ2 are heat added both to T1 and heat taken from T2 in one cycle of engine. W is the mechanical work done on the engine.
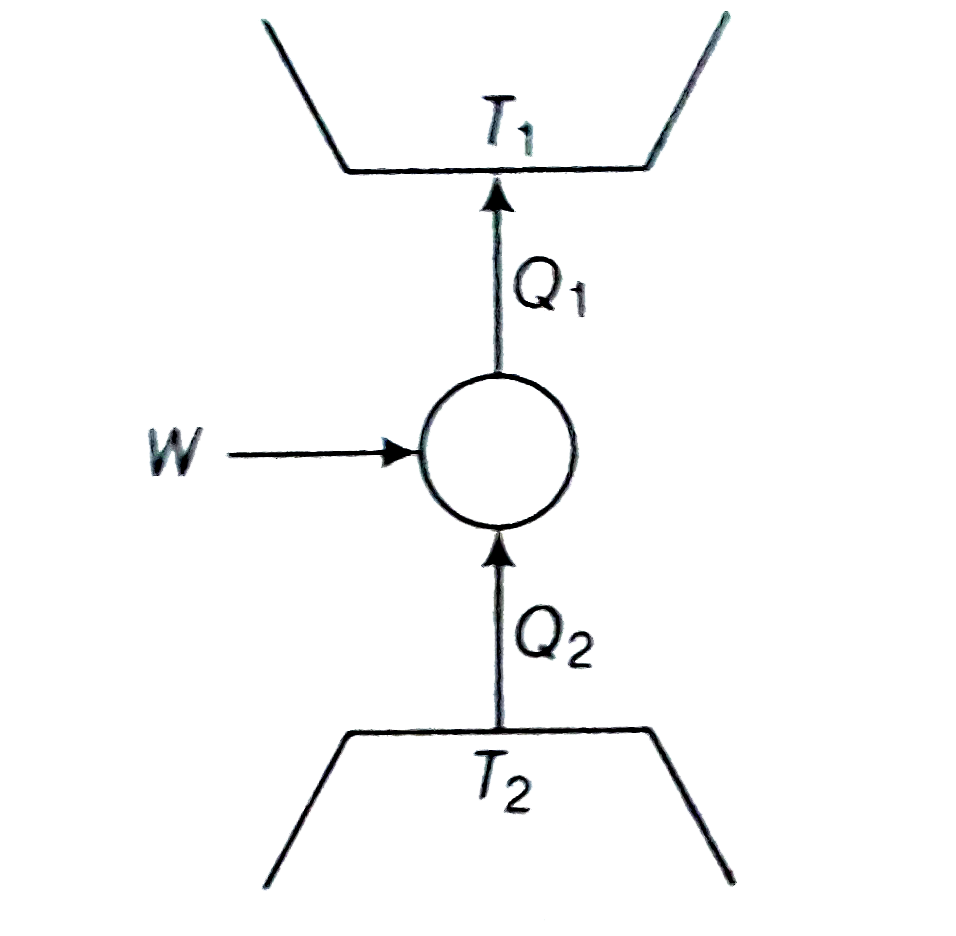
If W>0, then possibilities are
View SolutionA Carnot engine, having an efficiency of η=110 as heat engine, is used as a refrigerator. If the work done on the system is 10 J, the amount of energy absorbed from the reservoir at lower temperature is
View SolutionA Carnot engine, having an efficiency of η=110 as heat engine, is used as a refrigerator. If the work done on the system is 10 J, the amount of energy absorbed from the reservoir at lower temperature is
View SolutionA Carnot engine, having an efficiency of η=1/10 as heat engine, is used as a refrigerator. If the work done on the system is 10J, the amount of energy absorbed from the reservoir at lower temperature is
View SolutionA Carnot engine, having an efficiency of η=1/10 as heat engine, is used as a refrigerator. If the work done on the system is 10J, the amount of energy absorbed from the reservoir at lower temperature is
View SolutionA Carnot engine, having an efficiency of η=110 as heat engine, is used as a refrigerator. If the work done on the system is 10 J, the amount of energy absorbed from the reservoir at lower temperature is
View Solution