Centripetal and Centrifugal Force
Step-by-Step Solution:
Step 1: Understanding Circular Motion
- Circular motion refers to the movement of an object along the circumference of a circle or a circular path. In this motion, two key forces come into play: centripetal force and centrifugal force.
Step 2: Define Centripetal Force
- Centripetal force is the force that acts on an object moving in a circular path, directed towards the center of the circle. It is necessary for maintaining circular motion.
Step 3: Formula for Centripetal Force
- The formula for centripetal force (F_c) can be expressed as:
Fc=mv2r
where:
- m = mass of the object,
- v = velocity of the object,
- r = radius of the circular path.
Step 4: Centripetal Acceleration
- The centripetal acceleration (a_c) experienced by the object is given by:
ac=v2r
This acceleration is directed towards the center of the circular path.
Step 5: Alternative Expression for Centripetal Force
- Centripetal force can also be expressed in terms of angular velocity (ω):
Fc=mω2r
where ω is the angular velocity.
Step 6: Define Centrifugal Force
- Centrifugal force is not a real force but rather a pseudo force. It is perceived by an object in circular motion when viewed from its own rotating frame of reference.
Step 7: Characteristics of Centrifugal Force
- Centrifugal force acts outward, away from the center of the circular path. It is equal in magnitude but opposite in direction to the centripetal force:
Fcf=mv2rorFcf=mω2r
Step 8: Summary of Forces
- In summary:
- Centripetal Force: Actual force acting towards the center, necessary for circular motion.
- Centrifugal Force: Apparent force acting outward, experienced in the rotating frame of reference.
- Circular motion refers to the movement of an object along the circumference of a circle or a circular path. In this motion, two key forces come into play: centripetal force and centrifugal force.
- Centripetal force is the force that acts on an object moving in a circular path, directed towards the center of the circle. It is necessary for maintaining circular motion.
- The formula for centripetal force (F_c) can be expressed as:
Fc=mv2r
where:
- m = mass of the object,
- v = velocity of the object,
- r = radius of the circular path.
- The centripetal acceleration (a_c) experienced by the object is given by:
ac=v2r
This acceleration is directed towards the center of the circular path.
- Centripetal force can also be expressed in terms of angular velocity (ω):
Fc=mω2r
where ω is the angular velocity.
- Centrifugal force is not a real force but rather a pseudo force. It is perceived by an object in circular motion when viewed from its own rotating frame of reference.
- Centrifugal force acts outward, away from the center of the circular path. It is equal in magnitude but opposite in direction to the centripetal force:
Fcf=mv2rorFcf=mω2r
- In summary:
- Centripetal Force: Actual force acting towards the center, necessary for circular motion.
- Centrifugal Force: Apparent force acting outward, experienced in the rotating frame of reference.
Similar Questions
Knowledge Check
Centrifugal force is:
Aa) a real forceBb) the force of reaction of centripetal forceCc) a fictitious forceDd) directed towards the centre of circular pathAssertion: Electrons in the atom are held due to coulomb forces.
Reason: The atom is stable only because the centripetal force due to Coulomb's law is balanced by the centrifugal force.Aif both assertion and reason are true and reason is the correct explanation of assertion.Bif both assertion and reason are true but reason is not the correct explanation of assertion.Cif assertion is true but reason is false.Dif both assertion and reason are false.
Assertion: The centripetal forces and centrifugal forces never cancel out.
Reason: They do not act at the same time.
View SolutionTwo identical balls 1 and 2 are tied to two strings as shown in figure. They are rotated about point O. Ball 1 is observed from ball 2, centrifugal force on ball 1 is F1. Similarly, ball 2 is observed from ball 1 and centrifugal force on ball 2 is F2, then

View SolutionAssertion If a particle is rotating in a circle, then centrifugal force is acting on the particle in radially outward direction .
Reason centrifugal force is equal and opposite to the centripetel force.
View SolutionCan you recall, what centrifugal force is, and think why a molecule with higher mass/density would sediment faster?
View SolutionA particle of mass m is moving in a circle of radius (r) with changing speed (v) the direction of centripetal force and tangential force are shown below the value of α is
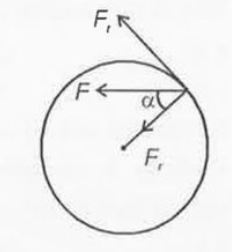
View SolutionA gramophone disc rotates at 60 rpm . A coin of mass 18 g is placed at a distance of 8 cm from the centre . Calculate centrifugal force on the coin . Take π2=9.87 .
View Solution
