River Boat Problem
To solve the River Boat Problem, we need to analyze the situation where a person wants to cross a river with a current. We will address two scenarios: the minimum time problem and the minimum distance problem.
Step 1: Define the Variables
- Let Vr be the velocity of the river (current).
- Let Vm be the velocity of the man (swimming speed).
- Let d be the width of the river.
- Let t be the time taken to cross the river.
Step 2: Minimum Time Problem
In the minimum time problem, the person aims to reach the opposite bank in the least amount of time. To achieve this:
- The person should swim perpendicular to the direction of the river's current.
- The resultant velocity Vresultant will be the vector sum of the man's swimming velocity and the river's current.
Using the Pythagorean theorem:
Vresultant=√V2m+V2r
The time taken to cross the river can be calculated as:
t=dVm
Step 3: Minimum Distance Problem
In the minimum distance problem, the person aims to reach directly across the river at point B while minimizing the distance traveled. To achieve this:
- The person must swim at an angle upstream against the current.
- The angle θ can be determined using the sine function:
sin(θ)=VrVm
The effective velocity across the river is:
Veffective=Vmcos(θ)
The time taken to cross the river in this scenario is:
t=dVeffective=dVmcos(θ)
Step 4: Calculate the Angle
To find the angle θ:
θ=sin−1(VrVm)
This angle indicates how much the person needs to swim against the current to reach point B directly.
Summary
- For minimum time, swim perpendicular to the current.
- For minimum distance, swim at an angle θ upstream, where sin(θ)=VrVm.
- Let Vr be the velocity of the river (current).
- Let Vm be the velocity of the man (swimming speed).
- Let d be the width of the river.
- Let t be the time taken to cross the river.
In the minimum time problem, the person aims to reach the opposite bank in the least amount of time. To achieve this:
- The person should swim perpendicular to the direction of the river's current.
- The resultant velocity Vresultant will be the vector sum of the man's swimming velocity and the river's current.
Vresultant=√V2m+V2r
t=dVm
In the minimum distance problem, the person aims to reach directly across the river at point B while minimizing the distance traveled. To achieve this:
- The person must swim at an angle upstream against the current.
- The angle θ can be determined using the sine function:
sin(θ)=VrVm
Veffective=Vmcos(θ)
t=dVeffective=dVmcos(θ)
To find the angle θ:
θ=sin−1(VrVm)
- For minimum time, swim perpendicular to the current.
- For minimum distance, swim at an angle θ upstream, where sin(θ)=VrVm.
Similar Questions
Two boats A and B having same speed relative to river are moving in a river. Boat A moves normal to the river current as observed by an observer moving with velocity of river current. Boat B moves normal to the river as observed by the observer on the ground.
View SolutionDrift is distance along a river a boat covers in crossing the river. If the boat reaches point C, distance BC is called downstream drift and if the boat reaches point D, distance BD is called upstream drift. To cross a river without drift, what should be relation between vbr and vr . If a boat crosses a river without drift, in which direction must it be steered.
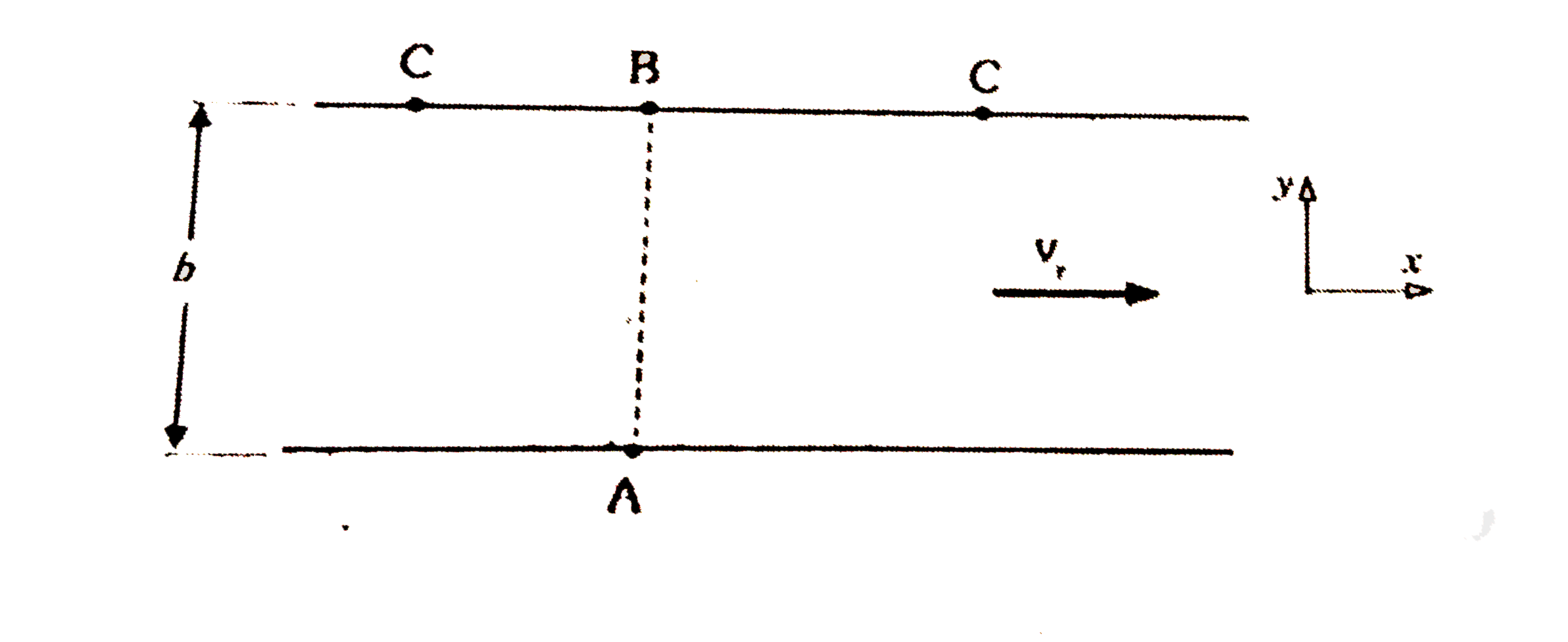
View SolutionA boat is rowed across a river at the rate of 4.5kmhr. The river flows at the rate of 6kmhr. The velocity of boat in ms is:
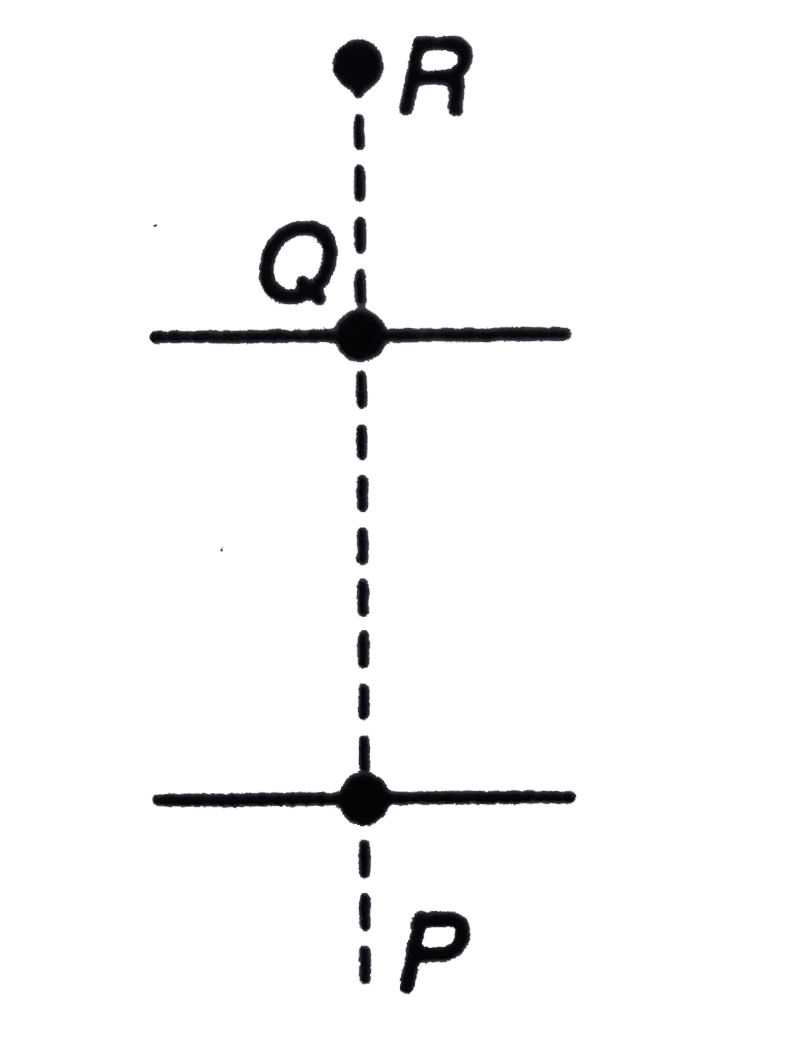
View SolutionA river of width ω is flowing with a uniform velocity v. A boat starts moving from point P also With velocity v relative to the river. The direction of resultant velocity is always perpendicular to the line joining boat and the fixed point R. Point Q is on the opposite side of the river. P, Q and R are in a straight line. If PQ=QR=ω, find (a) the trajectory of the boat, (b) the drifting of the boat and (c) the time taken by the boat to cross the river.
View SolutionTwo persons P and Q crosses the river starting from point A on one side to exactly opposite point B on the other bank of the river. The person P crosses the river in the shortest path. The person Q crosses the river in shortest time and walks back to point B. Velocity of river is 3 kmph and speed of each boat is 5 kmph w.r.t river. If the two persons reach the point B in the same time, then the speed of walk of Q is
View SolutionA,B and C are three persons who can row their boats with speeds 10 m/s 7 m/s and 3 m/s respectively in still water Velociy of flow of water in a river is 7 m/s All start rowing their boats upstream then
View SolutionA boat which travels at the rate of 10.5 km/hr downstream takes 3 times as long time to go to a certain distance up a river as to go the same distance down. Find the rate at which stream flows.
View SolutionA river is flowing towards with a velocity of 5ms−1. The boat velocity is 10ms−1. The boat crosses the river by shortest path. Hence,
View SolutionA river is flowing towards with a velocity of 5ms−1. The boat velocity is 10ms−1. The boat crosses the river by shortest path. Hence,
View SolutionA boat moves relative to water with a velocity which is 'n' times the river flow
a) If n<1 boat can not cross the river
b) If n = 1 boat can not cross the river without drifting
c) If n>1 boat can cross the river along shortest path
d) Boat can cross the river what ever is the value of n excluding zero value
View Solution
